Вычисление площадей плоских фигур

1.

Тема урока: «Вычисление
площадей плоских фигур»
(записать все примеры в
тетрадь)

2.

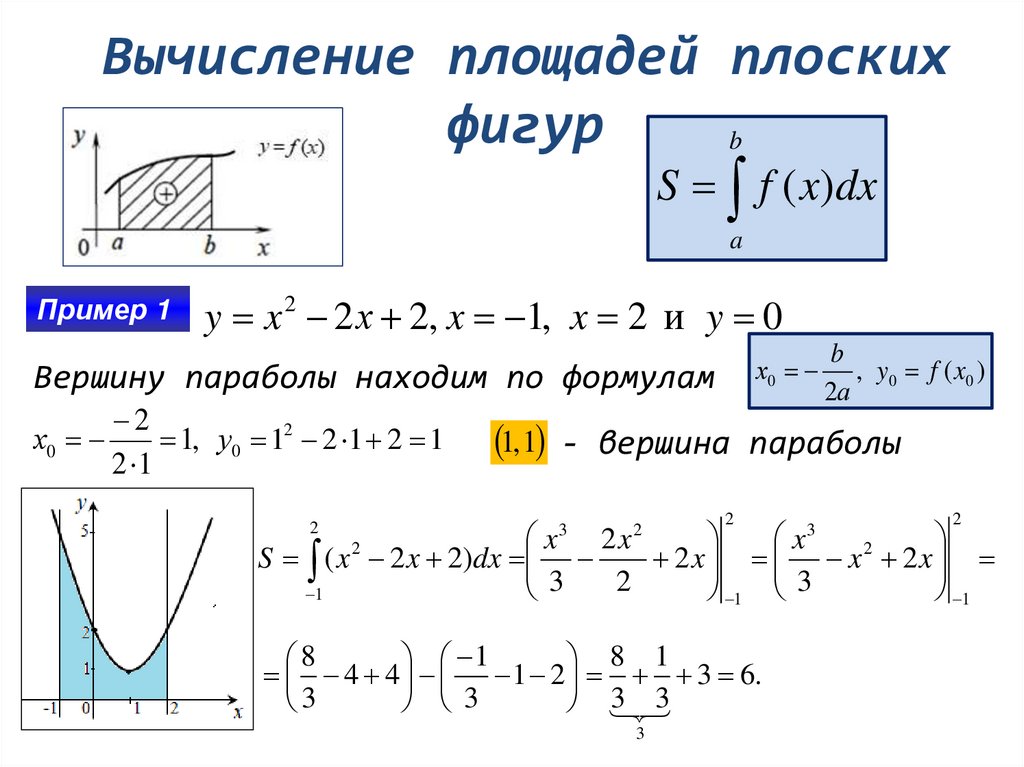
Вычисление площадей плоских
фигур
b
S f ( x)dx
a
Пример 1
y x 2 2 х 2, x 1, x 2 и y 0
х0
Вершину параболы находим по формулам
2
х0
1, у0 12 2 1 2 1
2 1
b
, y0 f ( x0 )
2а
1, 1 - вершина параболы
2
2
x 2x
x
S ( x 2 2 x 2)dx
2 x x 2 2 x
2
3
1 3
1
1
2
3
2
8
1
8 1
4 4 1 2 3 6.
3
3
3
3
3
3

3.

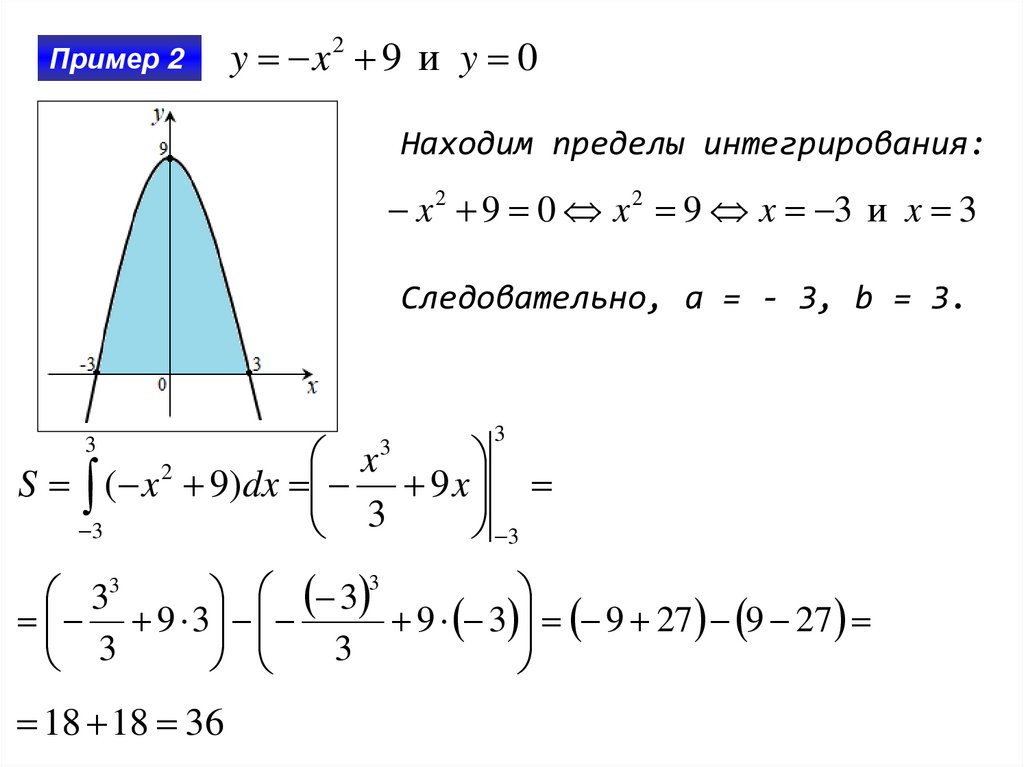
Пример 2
y x2 9 и y 0
Находим пределы интегрирования:
x 2 9 0 x 2 9 x 3 и x 3
Следовательно, a = - 3, b = 3.
3
x
S ( x 9)dx 9 x
3
3
3
3
3
2
33
3 3
9 3
9 3 9 27 9 27
3
3
18 18 36

4.

b
b
a
a
S f ( x)dx f ( x)dx
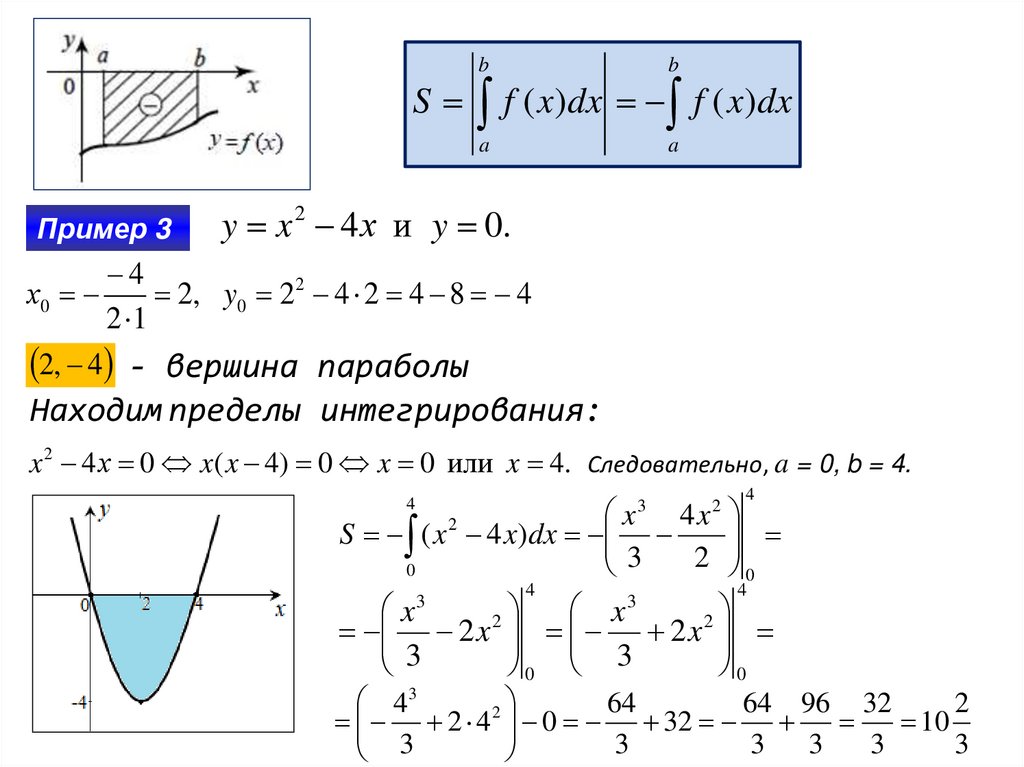
Пример 3
х0
y x 2 4 х и y 0.
4
2, y0 2 2 4 2 4 8 4
2 1
2, 4 - вершина параболы
Находим пределы интегрирования:
x 2 4 х 0 x( x 4) 0 x 0 или x 4. Следовательно, a = 0, b = 4.
4
x 4x
S ( x 4 x)dx
2 0
3
0
4
3
2
2
4
4
x
x
2
2
2 x 2 x
3
0 3
0
3
3
43
64
64 96 32
2
2
2 4 0 32
10
3
3
3
3
3
3

5.

b
S ( f 2 ( x) f1 ( x)) dx
a
Пример 5
y x 2 2 х 8 и y x 6.
2
х0
1, y0 12 2 1 8 9
2 1
1, 9 - вершина параболы.
Находим пределы интегрирования:
x2 2х 8 x 6
x2 2х 8 x 6 0
x2 х 2 0
x1 1 и x2 2 a 1, b 2
y1 1 6 5, y2 2 6 8

6.

1, 5 , 2, 8 - точки пересечения
параболы и прямой
2
2
3
2
2
x
x
2
S
x
2
x 8
x 6 dx x x 2 dx 2 x
f
(
x
)
3 2
1
f2 ( x)
1
1
1
2
x
23 2 2
1 3 1 2
x
2 x 2 2
2 1
3
2
3 2
1 3 2
3
2
2
8
1 1
1
8
1 1
2 4 2 6 2 5 4,5
3
3 2
2
3
3 2

7.

Выполнить № 21.43 – 21.53 (все под
буквой а)