Вычисление площадей плоских фигур

1. Вычисление площадей плоских фигур.

12.12.2023
1

2.

Определение криволинейной трапеции
Y
f(x)
a
Y
f(x)
12.12.2023
a
b
X
b
X
Если на отрезке [a;b]
функция f(x) не
меняет знак, то
фигура, ограниченная
графиком f(x), осью Ох
и прямыми х=а, х=b,
называется
криволинейной
трапецией.
2

3.

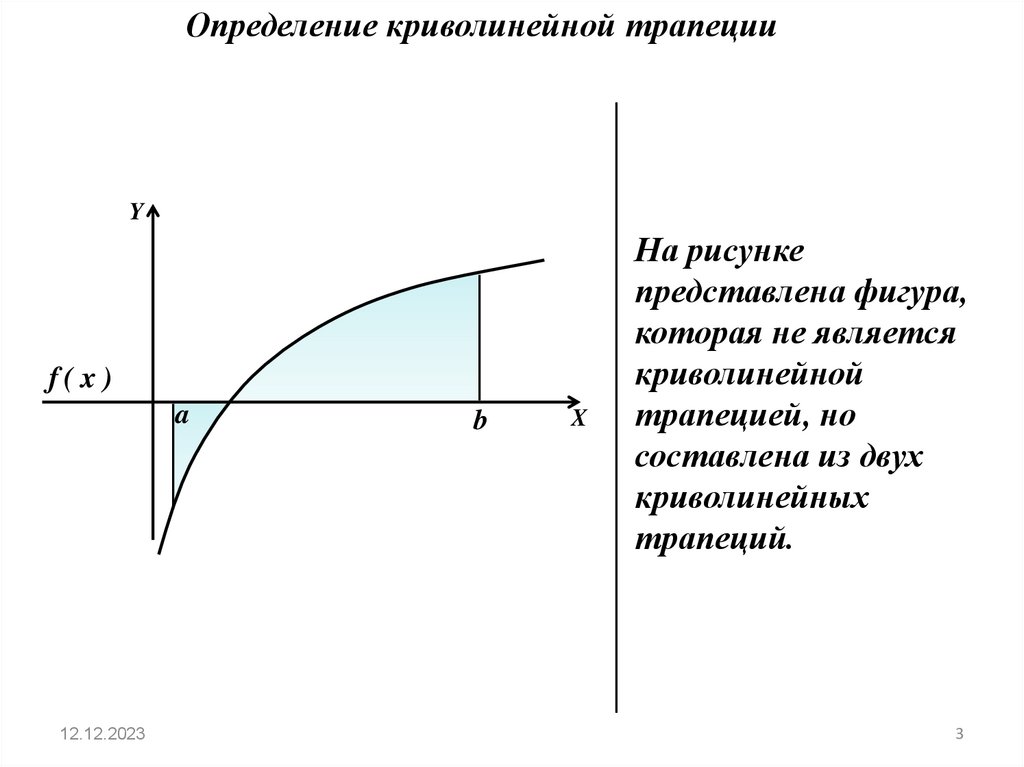
Определение криволинейной трапеции
Y
f(x)
a
12.12.2023
b
X
На рисунке
представлена фигура,
которая не является
криволинейной
трапецией, но
составлена из двух
криволинейных
трапеций.
3

4.

Геометрический смысл определенного интеграла
При хϵ[a;b] f(x)≥0.
Y
b
S f ( x )dx
a
f(x)
a
b
X
При хϵ[a;b] f(x)≤0.
Y
f(x)
a
b
X
b
S f ( x )dx
a
12.12.2023
4

5.

При решении задач на нахождение площадей плоских
фигур необходимо выяснить, какая фигура задана
условиями задачи.
Часто бывает достаточно схематического рисунка или
здравого смысла.
12.12.2023
5

6.

Вычислите площадь фигуры, ограниченной линиями:
Задача №1
y x 4 ; y 0 ; x 1; x 2
Решение:
Выясним, о какой фигуре идет речь.
Схематично изобразим график.
Y
f(x)≥0
2
1
2
X
5
x
4
S x dx
5
1
2
1
2 5 ( 1 )5
5
5
32 1 33
5 5
5
33 2
ед
Ответ:
5
12.12.2023
6

7.

Вычислите площадь фигуры, ограниченной линиями:
Задача №2
2
y
; y 0 ; x 1; x 4
x
Решение:
Попробуем обойтись без построения графика. Используем
здравый смысл.
D( y ) : x 0 На своей области определения функция знак
не меняет (у>0) и разрывов не имеет.
Таким образом даже без графика можно сделать вывод,
что речь идет о криволинейной трапеции первого типа.
4
S
1
12.12.2023
4
2
dx 4 x 4 4 4 1 8 4 4
1
x
Ответ: 4 ед 2
7

8.

Вычислите площадь фигуры, ограниченной линиями:
3
Задача №3 y 2 cos x ; y 0 ; x ; x
2
Решение: Данная функция меняет знак на своей области
определения (R). Выясним, о какой фигуре идет речь.
Y
Построим график.
(график функции
y=cosx растянут от 2
Ох в два раза).
3
5
1
X
2
2
2
2
2
3
2
Криволинейная
трапеция второго
3
типа.
2
S 2 cos xdx
3
2
2 cos xdx 2 sin x
12.12.2023
2 0 2
Ответ: 2 ед 2
8

9.

Как найти площадь фигуры, ограниченной двумя графиками
и прямыми х=а, х=b (см. рис.)
1 случай. Фигура расположена в верхней полуплоскости.
Y
Площадь можно найти как
разность площадей двух
криволинейных трапеций
первого типа.
f(x)
g( x )
a
X
b
b
b
a
a
S S f Sg f ( x )dx g( x )dx
разность интегралов равна интегралу разности =>
b
S ( f ( x ) g( x ))dx
a
12.12.2023
9

10.

Как найти площадь фигуры, ограниченной двумя графиками
и прямыми х=а, х=b (см. рис.)
2 случай. Фигура расположена в нижней полуплоскости.
Y
b
a
X
f(x)
Площадь можно найти как
разность площадей двух
криволинейных трапеций
второго типа.
g( x )
b
S S f S g g ( x )dx f ( x )dx
a
a
b
b
b
a
a
f ( x )dx g( x )dx
разность интегралов равна интегралу разности =>
b
S ( f ( x ) g( x ))dx
a
12.12.2023
10

11.

Как найти площадь фигуры, ограниченной двумя графиками
и прямыми х=а, х=b (см. рис.)
3 случай. Фигура расположена в двух полуплоскостях.
Y
f(x)
b
a
Площадь можно найти как
сумму площадей двух
криволинейных трапеций.
X
b
g( x )
S S f Sg
a
b
b
b
f ( x )dx g ( x )dx f ( x )dx g( x )dx
a
a
a
разность интегралов равна интегралу разности =>
b
S ( f ( x ) g( x ))dx
a
12.12.2023
Таким образом, для решения данной задачи не имеет
значения, где расположена фигура.
11

12.

Вычислите площадь фигуры, ограниченной линиями:
Задача №4
y x ; y 0 ,5 x 5 ; x 1; x 3
Решение: Построим фигуру.
y 0 ,5 x 5
Y
5
Воспользуемся
рассмотренным
правилом.
y x
b
1
X
3
S ( f ( x ) g( x ))dx
a
3
3
2
3
3x
S (( 0 ,5 x 5 ) x )dx ( 1,5 x 5 )dx
5x
4
1
1
1
3 ( 1 )2
3 9
27
3
5 3
5 ( 1 )
15 5 14
4
4
4
4
Ответ: 14 ед 2
12.12.2023
12

13.

Вычислите площадь фигуры, ограниченной линиями:
2
2
Задача №5 y x 4 x ; y ( x 4 )
Особенность задачи в том, что не указаны пределы интегрирования
вершина ( 2 ; 4 ) вершина ( 4 ;0 )
y x2 4 x
Y
1
2
Решение: Построим фигуру.
Пределы интегрирования – абсциссы
X Не забывайте, что графический способ требует
точек пересечения данных графиков.
4
проверки и подумайте, как быть, если точки
х=2 и х=4
пересечения графиков - не целые (следующая задача).
Воспользуемся правилом.
4
S ( ( x 4 )2 ( x 2 4 x ))dx
y ( x 4 )
2
2
4
4
4
3
2x
( x 8 x 16 x 4 x )dx ( 2 x 12 x 16 )dx
6 x 2 16 x
3
2
2
2
2 43
2 23
2
6 4 16 4 (
6 2 2 16 2 )
3
3
8 2
8
128
16
96 64
24 32
Ответ: ед
3
3
3
3
2
12.12.2023
2
2
13

14.

Вычислите площадь фигуры, ограниченной линиями:
2
2
Задача №5 y x 5 x ; y ( x 3 )
Решение: Построим фигуру.
вершина ( 2 ,5 ; 6 ,25 ) вершина ( 4 ;0 )
y x2 5 x
Y
1
X
?
Найдем пределы интегрирования:
y x2 5 x
2
y
(
x
3
)
x 2 5 x ( x 3 )2
x 1
x 4 ,5
9
2
S ( ( x 3 )2 ( x 2 5 x ))dx
y ( x 3 )
2
1
9
2
9
2
9
2
2 x 3 11 x 2
( x 6 x 9 x 5 x )dx ( 2 x 11 x 9 )dx
9x
3
2
1
1
1
Здесь разумно использовать приемы рационального счета.
Про калькулятор надо забыть!
2
12.12.2023
2
2
14

15.

Мы рассмотрели основные типы задач на
нахождение площадей плоских фигур.
Сформулируй условие для каждого типа и составь
алгоритмы.
Затем отработай алгоритмы воспользовавшись
задачником.
При необходимости обращайся за помощью.
12.12.2023
15