Линейная алгебра и аналитическая геометрия

1.

МАТЕМАТИКА

2.

Содержание дисциплины
Линейная алгебра и аналитическая
геометрия:
1. Матрицы
2. Определители
3. Системы линейных уравнений
4. Аналитическая геометрия
Математический анализ:
1. Предел функции
2. Дифференциальное исчисление

3.

Линейная алгебра

4.

МАТРИЦЫ. ОСНОВНЫЕ ПОНЯТИЯ
Матрицей называется прямоугольная таблица, составленная
из каких – либо элементов и имеющая m строк и n столбцов.
Элементами матрицы могут быть числа, алгебраические
выражения, функции и т.д.
a11
a 21
A
a
m1
a12 ... a1n
a 22 ... a 2n
am 2 ... amn
Матрицы обозначаются заглавными буквами латинского алфавита,
элементы матрицы – теми же маленькими буквами.
Размерность матрицы обозначается:
dim A m n
количество
количество
строк столбцов

5.

МАТРИЦЫ. ОСНОВНЫЕ ПОНЯТИЯ
Если m n , то матрица называется прямоугольной.
Если m n
порядка).
, то матрица называется
квадратной (n - ного
Любое число (скаляр) можно представить как матрицу первого
порядка, размерностью 1 1 .
Матрица типа 1 n называется матрица-строка:
a a
11
12
a13 ... a1n
Матрица типа m 1 называется матрица-столбец:
a11
a 21
...
a
m1

6.

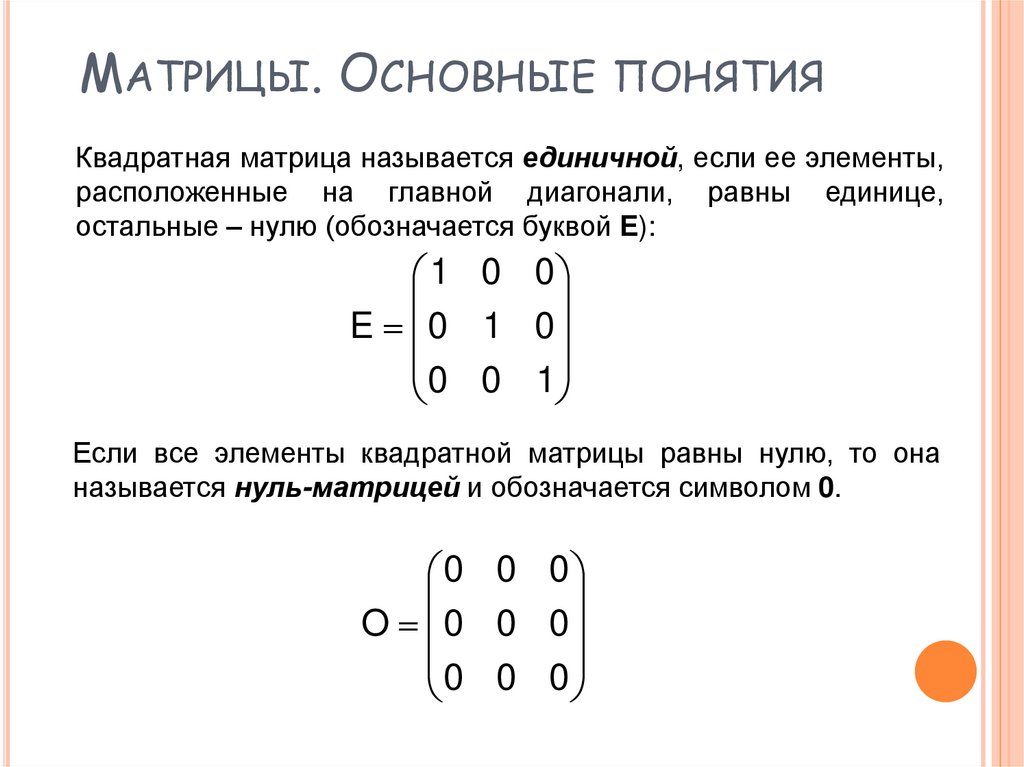
МАТРИЦЫ. ОСНОВНЫЕ ПОНЯТИЯ
Квадратная матрица называется единичной, если ее элементы,
расположенные на главной диагонали, равны единице,
остальные – нулю (обозначается буквой Е):
1 0 0
E 0 1 0
0 0 1
Если все элементы квадратной матрицы равны нулю, то она
называется нуль-матрицей и обозначается символом 0.
0 0 0
O 0 0 0
0 0 0

7.

ДЕЙСТВИЯ НАД МАТРИЦАМИ
Равенство матриц
Матрицы равны, если они имеют одинаковую размерность и их
соответствующие элементы равны.
A B
dim A dimB;
aij bij
Сложение (вычитание) матриц
Сумма и разность матриц существуют только для матриц
одинакового размера, при этом соответствующие элементы
матриц складываются или вычитаются.
C A B
dim A dimB dim C
c ij aij bij

8.

ДЕЙСТВИЯ (ОПЕРАЦИИ)НАД МАТРИЦАМИ
Пример. Найдите сумму и разность матриц А и В:
1 3 4
3 0 8
В
А
2 0 6
2 4 1
Тогда,
1 3 4 3 0 8 2 3 12
А В
2 0 6 2 4 1 4 4 5
1 3 4 3 0 8 4 3 4
А В
2 0 6 2 4 1 0 4 7
Транспонирование матрицы – осуществляется в результате
замены строк матрицы на соответствующие столбцы с
сохранением порядка элементов
1 5
Т
1 2 3
А 2 6
А
3 8
5 6 8

9.

Умножение матрицы на число
При умножении матрицы A на число k получается матрица того же
размера, при этом каждый элемент матрицы A умножается на k.
B k A
dim A dimB; bij aij k
3 5
Пример. Задана матрица А 0 2 , найти матрицу В=-2А.
3 5 6 10
В 2
0 2 0 4
Пример. Найти значение выражения: C A 5 B , где
1 3 2
A
0 1 4
2 4 1
B
5 0 2
3 5 ( 4) 2 5 1 11 17 7
1 5 2
C
0 5 ( 5) 1 5 0 4 5 2 25 1 14

10.

Умножение матриц
Произведение матриц A * B определено только тогда, когда
число столбцов матрицы А равно числу строк матрицы В, в
противном случае произведение не существует.
dim A m n
dim B n k
C A B существует
dimC m k
Произведением матрицы A размера [m n] с элементами aij
на матрицу B размера [n k ] с элементами bjq называется
матрица C размера [m k ] с элементами:
n
c iq aij b jq
j 1
А В В А

11.

1 0 2
A
3 1 4
0 5 1
B 2 1 1
3 2 0
0 5 1
B 2 1 1
3 2 0
1 0 2
A
3 1 4
6 9 1
14 24 4
Найти С = A * B
dim A 2 3
dim B 3 3
c12 1 5 0 1 2 2
c11 1 0 0 2 2 3
c13 1 1 0 1 2 0
6 9 1
C
14 24 4
cc22 33 5 1 11 1
44 20
1
c 21 3 023 1 2 4 3

12.

МАТРИЦЫ. ОСНОВНЫЕ ПОНЯТИЯ
Для каждой квадратной матрицы n - ного порядка существует
определитель n - ного порядка, элементы которого равны
соответствующим элементам матрицы.
a11 a12
A a21 a22
a
31 a32
a13
a23
a33
a11 a12
det A a21 a 22
a31 a32
a13
a 23
a33
Определитель любой единичной матрицы равен единице.
Если определитель матрицы равен нулю, то
называется вырожденной, в противном случае
невырожденная.
матрица
матрица

13.

ОПРЕДЕЛИТЕЛИ 2 ПОРЯДКА
Определители широко применяются во многих разделах
высшей математики, в теоретической механике, физике и т.д.
для сокращения записей и удобства вычислений.
Определитель 2 - го порядка это число, записанное в виде:
a11 a12
a11a22 a12a21
a 21 a 22
ai j
Номер строки
Элементы определителя,
Индексы
Номер столбца
из произведения элементов главной диагонали вычитается
Главная
диагональ
произведение элементов
побочной
диагонали.
определителя
Побочная диагональ
определителя

14.

МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ
1
Метод треугольника
+
1 3 0
2 1 4
5 6 1
_
1 ( 1) 1 3 4 5 2 6 0 5 ( 1) 0
2 3 1 1 6 4 29
Метод треугольника применим только для определителей 3 порядка

15.

МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ
2
Метод разложения определителя по элементам строки
(столбца)
Определитель второго порядка, который получается из определителя
3 - го порядка путем вычеркивания i - й строки и j - го столбца, т.е.
строки и столбца, на пересечении которых стоит элемент ai j
называется минором элемента и обозначается Mi j
Алгебраическим дополнением элемента ai j называется
Ai j Mi j ( 1)i j
aa1111 aa1212 aa1313
aa2121 aa2222 aa2323
aa3131 aa3232 aa3333
aa2211 aa2312
MM1123
aa3231 aa3332
1 1 2 3
A
M
(
M23
A11 23 M11 23( 1) 1) M
11

16.

МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ
Величина определителя равна сумме произведений элементов
какой – либо строки (столбца) определителя на их
алгебраические дополнения:
n
ai j A i j
Разложение определителя по элементам
i – ой строки
ai j A i j
Разложение определителя по элементам
j – ого столбца
j 1
n
i 1
2 1 0
0 1
0 3
3 1
1 2
1 1
0 3 1 2
( 1) 0
( 1)1 3
( 1) 1
2 1
2 5
5 1
2 5 1
2 (3 1 5 1) 1 (0 1 2 1) 2

17.

ПРЕОБРАЗОВАНИЯ НАД СТРОКАМИ (СТОЛБЦАМИ) МАТРИЦЫ
1) можно менять строки (столбцы) местами;
2) можно умножать элементы строки на одно и то же число,
отличное от нуля;
3) можно складывать (вычитать) строки друг с другом.
Верхнетреугольная матрица, у которой под главной
диагональю все элементы равны нулю, называется
приведенной к ступенчатому виду. При этом элементы,
стоящие на главной диагонали называются угловыми
элементами.
Ранг матрицы А – это максимальное число линейно
независимых строк этой матрицы.

18.

ПРИВЕДЕНИЕ МАТРИЦЫ К СТУПЕНЧАТОМУ ВИДУ
Пример.
2
1
А
1
1
1 1
2 0
3 0
4 1
1
2
А
1
1
2
1
3
4
1 Поменяем вторую и первую строки местами
1 (для ручного счёта удобно, чтобы элемент
1 был равен 1 или -1, если это возможно).
2 Получим:
1 Теперь с помощью элемента =-1 образуем
1 нули в 1-ом столбце. Для этого ко 2-й строке
1 прибавим 1-ю, умноженную на 2, из 3-й
2 строки вычтем 1-ю строку, к 4-й прибавим
1 2 0 1 первую строку. Получим:
0
0
0
0
1
0
1
5 1 3
1 0 0
6 1 3

19.

ПРИВЕДЕНИЕ МАТРИЦЫ К СТУПЕНЧАТОМУ ВИДУ
Поменяем местами в этой матрице вторую и третью строки, и в
дальнейшем первая и вторая строки меняться не будут. И с
помощью элемента 1 получим нули во втором столбце в
третьей и четвертой строках:
1 2 0 1
1 2 0 1 Здесь из третьей строки
вычли 2-ю, умноженную
0 1 0 0
0 1 0 0
0 5 1 3 0 0 1 3 на 5; а из 4-й – вторую,
умноженную на 6.
0
6 1 3
1
0
0
0
2
1
0
0
0
0
1
0
0
0 1 3
1 Из четвертой строки вычтем третью.
0 Угловые элементы -1, 1, 1, их число равно 3,
3 Следовательно, ранг матрицы равен 3.
0
rangA R( A) 3

20.

ОБРАТНАЯ МАТРИЦА
Матрица А-1 называется обратной к матрице А, если
выполняется условие А· А-1= А-1·А=Е.
Теорема. Матрица А имеет обратную А-1 тогда и только
тогда, когда det A≠0.
Способы вычисления обратной матрицы
1. Метод Гаусса вычисления обратной матрицы
Припишем к матрице А единичную матрицу того же порядка:
а11 а12 ... а1n 1 0 ... 0
а21 а22 ... а2 n 0 1 ... 0
( А Е)
...
... ... ... ... ... ... ...
аn1 аn 2 ... аnn 0 0 ... 1
С помощью элементарных преобразований приведем
матрицу А Е Е А 1

21.

ОБРАТНАЯ МАТРИЦА
Вычисление обратной матрицы с помощью алгебраических
дополнений:
1) вычисляют определитель матрицы det A;
2) для каждого элемента a ij вычисляют алгебраические
дополнения Aij ;
~
3) составляют матрицу A из алгебраических дополнений:
A11
~ A21
A
...
A
n1
A12
A22
...
An 2
...
...
...
...
A1n
A2 n
...
Ann
4) транспонируют матрицу , её называют присоединённой:
A11 A21 ... An1 5) обратную матрицу определяют
~ T A12 A22 ... An 2 по формуле:
A
1
~T
...
... ... ...
1
A
A
A
det A
1n A2 n ... Ann

22.

ОБРАТНАЯ МАТРИЦА
2 1 4
Пример. Найти матрицу, обратную к матрице A 1 0 2
3 5 8
Решение. 1) det A=0+20-6-0+20+8=42;
0 2
2) A11
0 10 10;
5 8
2 4
A22
2 8 4 ( 3) 28;
3 8
1 2
A12
(8 6) 2;
3 8
2 1
A23
(2 5 ( 1) ( 3)) 7;
3 5
1 0
A13
5 0 5;
3 5
1 4
A31
( 1) ( 2) 4 0 2;
0 2
1 4
A21
( 8 20) 28;
5 8
2 4
A32
( 4 4) 8;
1 2
2
A33
1
1
0 1 1.
0

23.

ОБРАТНАЯ МАТРИЦА
10 28 2
~T
4) A 2 28 8 ;
5 7 1
10 28 2
1
1
5) Получили обратную матрицу: А
2 28 8
42
5 7 1
Сделаем проверку, убедимся, что полученная матрица искомая:
10 2 5
~
3) A
28 28 7 ;
2 8
1
10 28 2 1 0 0
2 1 4
1
-1
А· А = 1
0 2
2 28 8 = 0 1 0 Е .
42
0 0 1
3 5
5
7
1
8

24.

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Система, состоящая из m уравнений с n переменными, это
выражение вида:
a11 x1 a12 x2 ... a1n xn b1
a12 x1 a22 x2 ... a2 n xn b2
.................................................
am1 x1 am 2 x2 ... amn xn bm
a11 a12
a 21 a 22
А
... ...
a
m1 a m 2
... a1n
... a 2 n
- матрица коэффициентов при
... ...
переменных
... a mn

25.

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
b1
х1
х2 - матрица переменных; B b2 - матрица свободных
Х
...
...
членов
b
х
m
n
Матричная запись системы линейных уравнений имеет вид:
AX b.
а11 а12
а21 а22
Матрица А
... ...
аm1 аm 2
... а1n b1
... а2 n b2
называется расширенной.
... ... ...
... аmn bm

26.

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Виды систем линейных уравнений
1. Если вектор b=0, то система называется однородной, если
b≠0 (хотя бы один из свободных членов отличен от нуля), то
система называется неоднородной.
2. Система, имеющая хотя бы одно решение, называется
совместной, в противном случае – несовместной.
3. Две системы называются эквивалентными, если
множества их решений совпадают.
Заметим, что операции над системой уравнений сводятся к
элементарным преобразованиям над расширенной
матрицей.

27.

МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Методы решения неоднородных систем уравнений
1. Метод Гаусса – заключается в том, что расширенная
матрица приводится к ступенчатому виду.
2 х1 х2 х3 3
Пример. Решите систему уравнений х1 3х3 2
х 2х х 4
2
3
1
х1
2 1 1
3
Решение: А 1 0 3 , Х х2 , B 2
1 2 1
х
4
3
. Расширенная матрица имеет вид:
2 1 1 3
А 1 0 3 2
1 2 1 4

28.

МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
2
1
1
1
0
2
1 3
1
3 2 1
2
1 4
2
0
1
1 4
1
3 2 0
0
1 3
1
0
0
2
1
5
1 4
1
1 1 0
0
3 5
2
1
0
1 4
1 1
8 0
2
2
5
1 4
2 2
3 5
Перейдём от матричной записи к записи системы уравнений:
1) 32 х3 0 х3 ;0
2 х1 х2 х3 3
х2 7 х3 1
32 х 0
3
2) х2 7 0 1 х2 1 х2 1;
3) 2 х1 1 0 3 2 х1 4 х1 2.
Ответ: Х (2; 1; 0).

29.

МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
2. Метод Крамера, основан на теореме:
Теорема. Система AX b , где det A≠0, имеет единственное
решение, которое вычисляется по формулам:
n
1
2
х1
, х2
,..., хn
где Δ= det A, Δi - получается из определителя Δ заменой
i-го столбца на столбец свободных членов.
Пример (из метода 1):
2 1 1
1 0
3 0 ( 2) ( 3) 0 12 ( 1) 16;
1
2 1

30.

МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
3
1 2
4
1
0
2
1
3 0 ( 4) ( 12) 0 18 ( 2) 32;
1
2
2 1
1
3
2
4
1
3 4 ( 4) 9 ( 2) 24 3 16;
1
2
3 1
1
1
0
2
3
2 0 ( 6) 2 0 4 ( 8) 0.
4
3
1 32
2 16
0
х1
2; х2
1; х3
0.
16
16
16
Ответ: Х (2; 1; 0).

31.

МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
3. Метод решения системы уравнений с помощью
обратной матрицы:
1
Х А В
Пример (из метода 1).
2 1 1
А 1 0
3 ;
1
2
1
6
1
1
Х А В 2
16
2
Ответ: Х (2; 1; 0).
6
1
1
А 2
16
2
1
3
5
1
3
5
3
7 ;
1
3 3
32 2
1
7 2 16 1
16
0
1 4
0

32.

Аналитическая геометрия

33.

ВЕКТОРЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
Вектор – это направленный отрезок (отрезок, для которого
указано его начало и его конец).
Виды векторов:
1) Коллинеарные векторы – это векторы, лежащие на одной
прямой или на параллельных прямых:
а) Сонаправленные векторы;
б) Противоположено направленные.
2) Неколлинеарные векторы – векторы,
не лежащие на одной прямой, или на
параллельных прямых.

34.

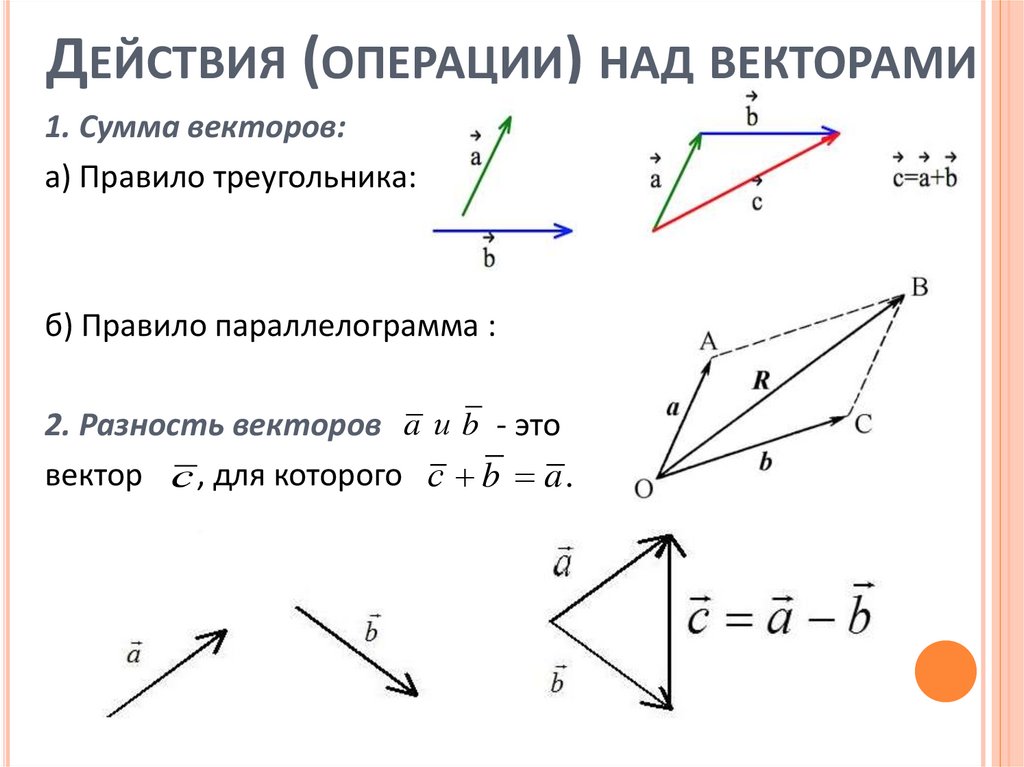
ДЕЙСТВИЯ (ОПЕРАЦИИ) НАД ВЕКТОРАМИ
1. Сумма векторов:
а) Правило треугольника:
б) Правило параллелограмма :
2. Разность векторов a и b - это
вектор с , для которого с b a .

35.

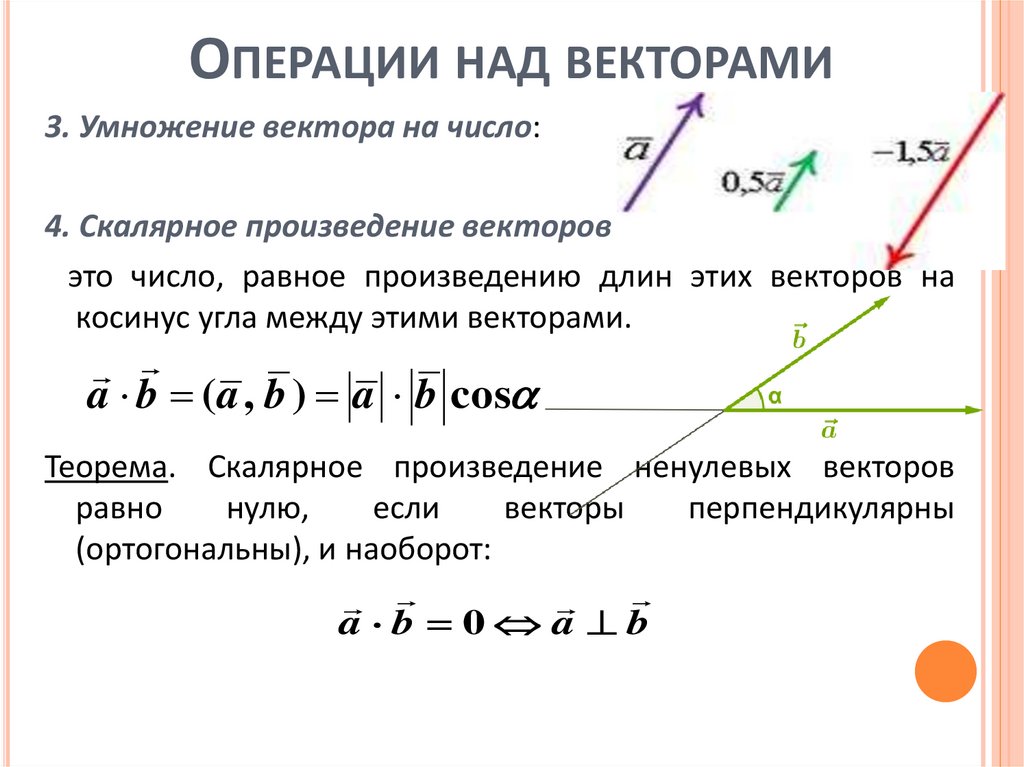
ОПЕРАЦИИ НАД ВЕКТОРАМИ
3. Умножение вектора на число:
4. Скалярное произведение векторов –
это число, равное произведению длин этих векторов на
косинус угла между этими векторами.
a b (a , b ) a b cos
Теорема. Скалярное произведение ненулевых векторов
равно
нулю,
если
векторы
перпендикулярны
(ортогональны), и наоборот:
a b 0 a b

36.

ОПЕРАЦИИ НАД ВЕКТОРАМИ
5. Векторное произведение векторов a и b - это вектор с ,
который удовлетворяет следующим условиям:
1) с а b sin ;
2) с а и с b ;
3) векторы образуют «правую» тройку
векторов.
Обозначение: a b
Теорема. Модуль векторного произведения (длина вектора)
численно равен площади параллелограмма, построенного на
векторах a и b :
S парал. a b

37.

ОПЕРАЦИИ НАД ВЕКТОРАМИ
6. Смешанное произведение трёх векторов а , b и с –
это число, равное скалярному произведению вектора а b
на вектор с .
Теорема. Объем V треугольной пирамиды, построенной на
трёх векторах вычисляется по формуле:
1
V ab c
6

38.

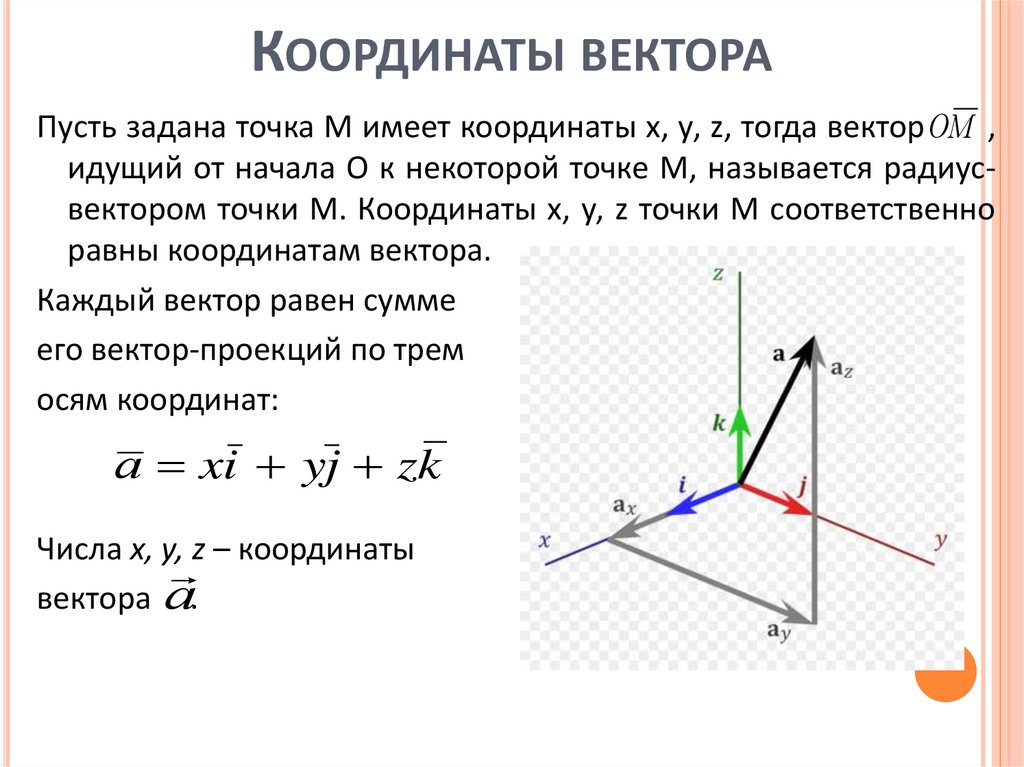
КООРДИНАТЫ ВЕКТОРА
Пусть задана точка М имеет координаты х, у, z, тогда вектор ОМ ,
идущий от начала О к некоторой точке М, называется радиусвектором точки М. Координаты х, у, z точки М соответственно
равны координатам вектора.
Каждый вектор равен сумме
его вектор-проекций по трем
осям координат:
а xi yj zk
Числа х, у, z – координаты
вектора а.

39.

ОПЕРАЦИИ НАД ВЕКТОРАМИ В КООРДИНАТНОЙ ФОРМЕ
1. При сложении векторов, заданных в координатной форме,
их координаты складываются.
2. При вычитании векторов, заданных в координатной
форме, их координаты вычитаются.
3. При умножении вектора на число надо все его координаты
умножить на это число.
4. Скалярное произведение векторов, заданных в
координатной форме, определяется числом вида
(а , b ) a b x1 x2 y1 y 2 z1 z 2

40.

ОПЕРАЦИИ НАД ВЕКТОРАМИ В КООРДИНАТНОЙ ФОРМЕ
5. Векторное произведение векторов а ( х1 , y1 , z1 ) и b ( х2 , y 2 , z 2 )
в координатной форме вычисляется следующим образом:
i
а b x1
x2
6.
j
y1
y2
k
y1
z1 i
y2
z2
z1
x1
j
z2
x2
Смешанное произведение в
вычисляется следующим образом:
x1
a b c x2
x3
z1
x1
k
z2
x2
y1
.
y2
координатной
y1 z1
y2 z2 .
y3 z 3
форме

41.

ОПЕРАЦИИ НАД ВЕКТОРАМИ В КООРДИНАТНОЙ ФОРМЕ
Пример 1. Найдите косинус угла между векторами с 3а 2b
и d а 2b , где а ( 1; 2; 0), b (3; 1; 2).
Решение:
1) с 3а 2b 3( 1; 2; 0) 2(3; 1; 2) ( 3; 6; 0) (6; 2; 4) ( 9; 4; 4)
d а 2b ( 1; 2; 0) 2(3; 1; 2) ( 1; 2; 0) (6; 2; 4) (5; 4; 4)
2) c d 9 5 4 4 4 ( 4) 45;
3) Длину каждого вектора определим по формуле: а х 2 y 2 z 2
2
2
2
2
2
2
d
5
4
(
4
)
57 .
c ( 9) 4 4 113;
c d
45
45
4) cos
.
113 57
6441
c d

42.

ОПЕРАЦИИ НАД ВЕКТОРАМИ В КООРДИНАТНОЙ ФОРМЕ
Пример 2. Вычислить площадь
треугольника, построенного на
векторах а ( 1; 2;0) и b (3; 1; 2).
Решение:
1
S S парал.
2
a b
2
i j
k
n а b 1 2
0 4i k 6k 2 j 4i 2 j 7k
3 1 2
n ( 4; 2; 7), n ( 4) 2 ( 2) 2 ( 7) 2 69 .
S
69
.
2

43.

ОПЕРАЦИИ НАД ВЕКТОРАМИ В КООРДИНАТНОЙ ФОРМЕ
Пример 3. Вычислите объём
пирамиды, построенной на
векторах а ( 1; 2;0) , b (3; 1; 2) , с (2; 4; 5).
Решение:
1
ab c 3
2
2
1
4
0
2 5 8 8 30 35;
5
1
35
V 35
5,83.
6
6

44.

ПРЯМАЯ И ЕЁ УРАВНЕНИЯ
Линии на плоскости соответствует некоторое уравнение с
двумя переменными х и у F ( x, y) 0 , которому
удовлетворяют координаты любой точки, лежащей на
линии, и не удовлетворяют координаты ни одной точки, не
лежащие на ней. Такое уравнение называется уравнением
данной линии.
Всякая прямая в декартовой система координат может быт
представлена уравнением первой степени и, наоборот,
всякое уравнение первой степени относительно х и у
определяет прямую линию.

45.

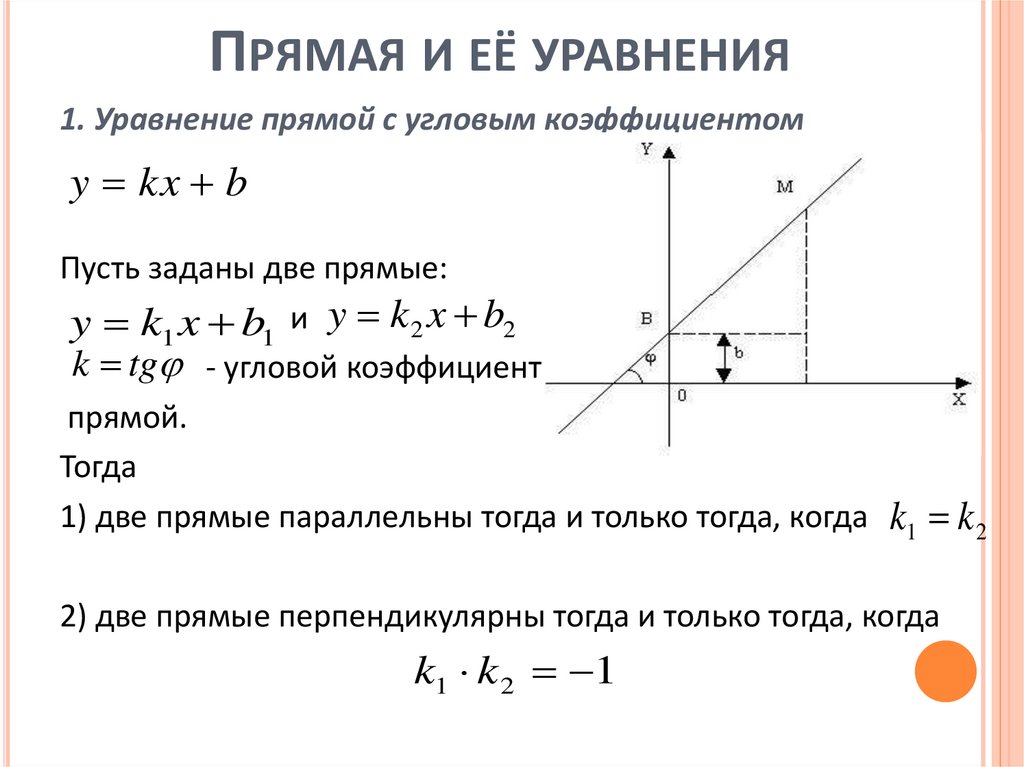
ПРЯМАЯ И ЕЁ УРАВНЕНИЯ
1. Уравнение прямой с угловым коэффициентом
y kx b
Пусть заданы две прямые:
y k1 x b1 и y k 2 x b2
k tg - угловой коэффициент
прямой.
Тогда
1) две прямые параллельны тогда и только тогда, когда k1 k 2
2) две прямые перпендикулярны тогда и только тогда, когда
k1 k 2 1

46.

ПРЯМАЯ И ЕЁ УРАВНЕНИЕ
2. Общее уравнение прямой
Ax By C 0
3. Уравнение прямой по двум точкам M ( x1 , y1 ) и N ( x2 , y 2 )
y y1
x x1
y 2 y1 x2 x1
4. Уравнение прямой с угловым коэффициентом k,
проходящей через точку М 0 ( х0 ; у 0 )
y y 0 k ( x x0 )
5. Уравнение прямой в отрезках
x
y
1.
a
b

47.

ПРЯМАЯ И ЕЁ УРАВНЕНИЕ
Пример. Треугольник АВС задан
координатами своих вершин: А(1; -3),
В(2; 5), С(8; 1). Найдите: 1) уравнение
медианы AD; 2) уравнение высоты
ВЕ; 3) средней линии, параллельной АС;
4) длину медианы и высоты.
Решение. 1) Найдём координаты D –
x x2 y1 y 2
;
середины отрезка ВС по формуле D 1
:
2 8 5 1
D
;
; D (5; 3)
2
2
2
2
Составим уравнение прямой AD по двум точкам А и D:
х 1 у ( 3) х 1 у 3
3
9
;
; 6( х 1) 4( у 3); 4 у 6 х 18; у х
5 1 3 ( 3) 4
6
2
2

48.

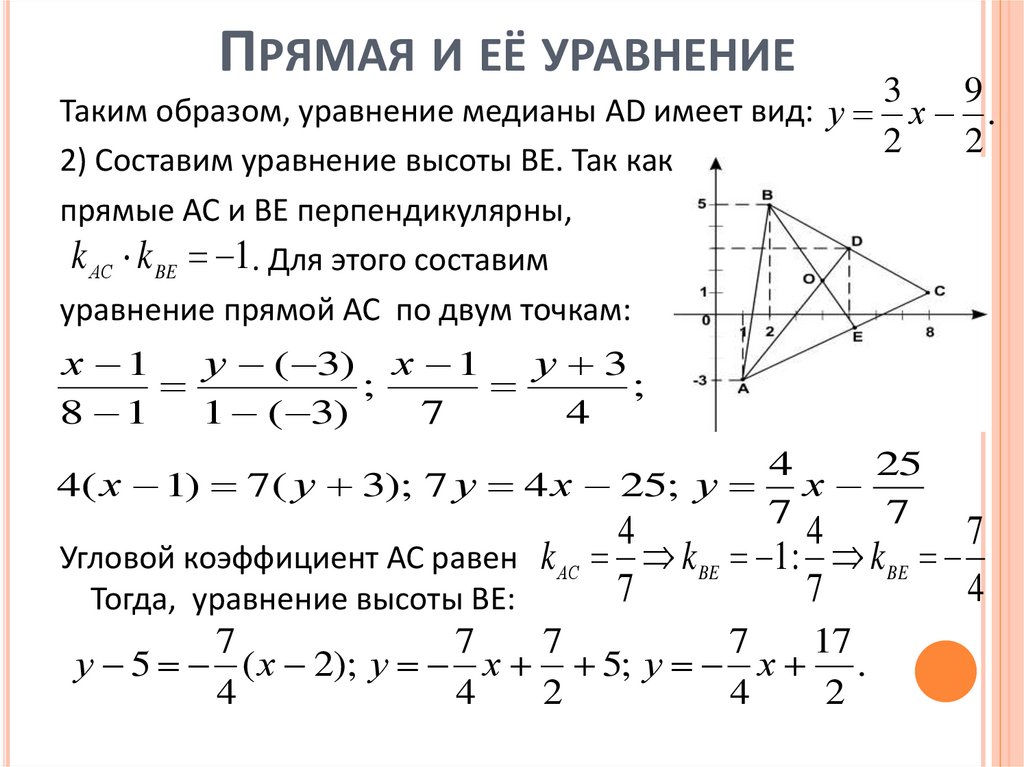
ПРЯМАЯ И ЕЁ УРАВНЕНИЕ
3
9
Таким образом, уравнение медианы AD имеет вид: у х .
2
2
2) Составим уравнение высоты ВЕ. Так как
прямые АС и ВЕ перпендикулярны,
k АС k BE 1. Для этого составим
уравнение прямой АС по двум точкам:
х 1
у ( 3) х 1
у 3
;
;
8 1
1 ( 3)
7
4
4
25
4( х 1) 7( у 3); 7 у 4 х 25; у х
7
7
4
4
7
Угловой коэффициент АС равен k АС k BE 1 : k BE
7
7
4
Тогда, уравнение высоты ВЕ:
7
7
7
7
17
у 5 ( х 2); у х 5; у х .
4
4
2
4
2

49.

ПРЯМАЯ И ЕЁ УРАВНЕНИЕ
3) Составим уравнение средней линии
КD, параллельной стороне АС. Так как
средняя линия параллельна АС, значит
4
k KD k AC
7
Составим уравнение КD по точке D и
4
4
20
4
1
угловому коэффициенту: у 3 ( х 5); у х 3; у х .
7
7
7
7
7
4) Найдём длину медианы по формуле:
АВ ( х2 х1 ) 2 ( у2 у1 ) 2
АD (5 1) 2 (3 ( 3)) 2 52 7,2 .

50.

ПРЯМАЯ И ЕЁ УРАВНЕНИЯ
Чтобы найти длину высоту, найдём координаты точки Е из
решения системы уравнений:
4
25
4
25
7
17
у х
х
х
;
7
7
7
7
4
2
;
4
7
17 25
у 7 х 17
х
х
;
4
2
7
4
2
7
65
169
х
;
28
14
338
х
5,2; у 0,6.
65
Тогда,
ВЕ (5,2 2) 2 ( 0,6 5) 2 41,6 6,5.

51.

КРИВЫЕ ВТОРОГО ПОРЯДКА
Уравнение вида Ax 2 2 Bxy Cy 2 2Dx 2Ey F 0
называется уравнением второго порядка.
1. Окружность – это геометрическое
место точек, равноудаленных от точки О
на расстояние R. Уравнение окружности:
( х а) 2 ( у b) 2 R 2 ,
где О(a; b) - центр окружности,
R – радиус окружности.
Замечание 1. Если начало координат совпадает с центром
окружности, то ее уравнение имеет вид:
х2 у2 R 2

52.

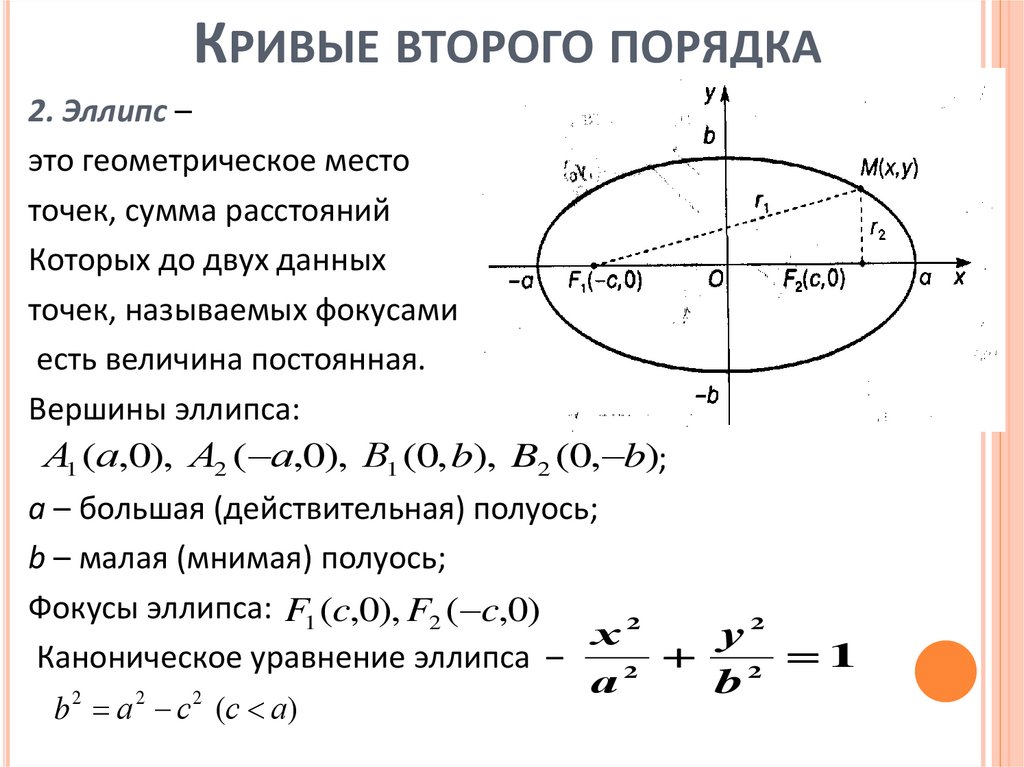
КРИВЫЕ ВТОРОГО ПОРЯДКА
2. Эллипс –
это геометрическое место
точек, сумма расстояний
Которых до двух данных
точек, называемых фокусами
есть величина постоянная.
Вершины эллипса:
А1 (а,0), А2 ( а,0), В1 (0, b), B2 (0, b);
а – большая (действительная) полуось;
b – малая (мнимая) полуось;
Фокусы эллипса: F1 (c,0), F2 ( c,0)
х2
у2
1
Каноническое уравнение эллипса –
2
2
а
b
2
2
2
b а с (с а)

53.

КРИВЫЕ ВТОРОГО ПОРЯДКА
Замечание 1. Если а b (c 0) , тогда каноническое уравнение
эллипса примет вид x 2 y 2 a 2 , и определяет окружность, а
значит, окружность можно рассматривать как частный случай
эллипса с равными полуосями.
с
Замечание 2. Число называется эксцентриситетом
а
эллипса.
Замечание 3. Если фокусы эллипса расположены на оси OY, то
эллипс «вытягивается» вдоль оси OY, тогда фокусы имеют
координаты F1 (0, с), F2 (0, с),
c.
2
2
2
с b a ;
b

54.

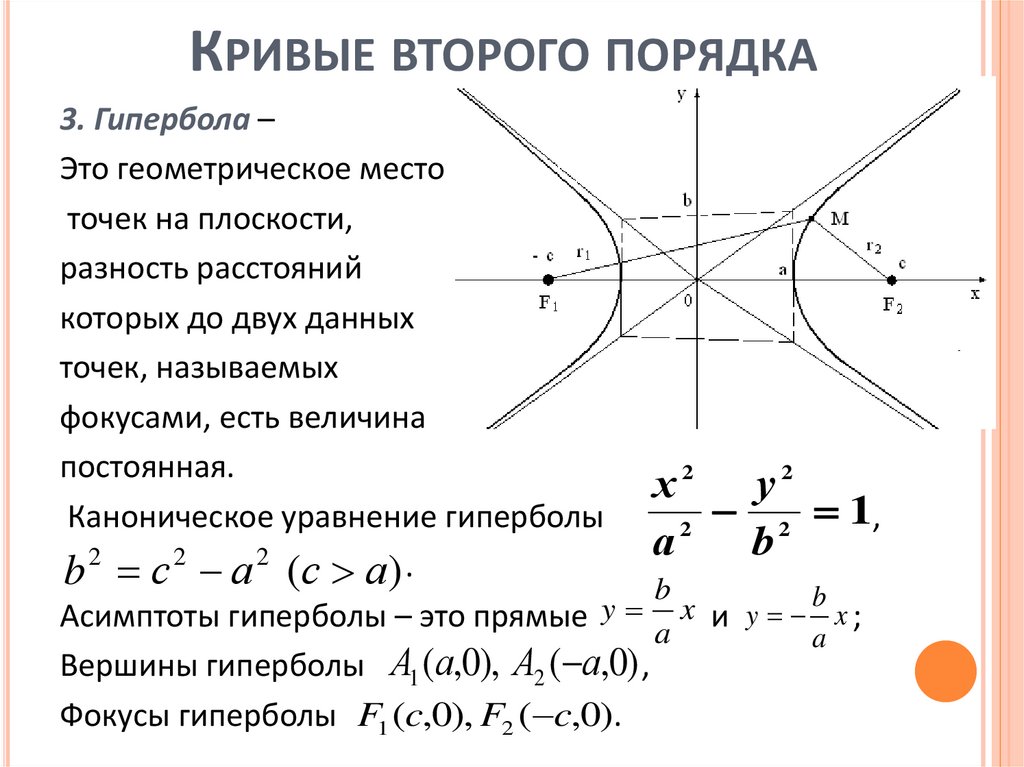
КРИВЫЕ ВТОРОГО ПОРЯДКА
3. Гипербола –
Это геометрическое место
точек на плоскости,
разность расстояний
которых до двух данных
точек, называемых
фокусами, есть величина
постоянная.
х2
у2
2 1,
Каноническое уравнение гиперболы
2
а
b
2
2
2
b с а (с а) .
b
b
y
x
y
x;
Асимптоты гиперболы – это прямые
и
a
a
Вершины гиперболы А1 (а,0), А2 ( а,0) ,
Фокусы гиперболы F1 (c,0), F2 ( c,0).

55.

КРИВЫЕ ВТОРОГО ПОРЯДКА
Замечание 1. Если мнимая ось
гиперболы расположена на оси ОУ
(a<b), то фокусы гиперболы
расположены на оси ОУ.
Замечание 2. При a=b гипербола
Называется равносторонней.
Замечание 3. Эксцентриситетом
гиперболы называется отношение
фокусного расстояния к
с
действительной оси .
а

56.

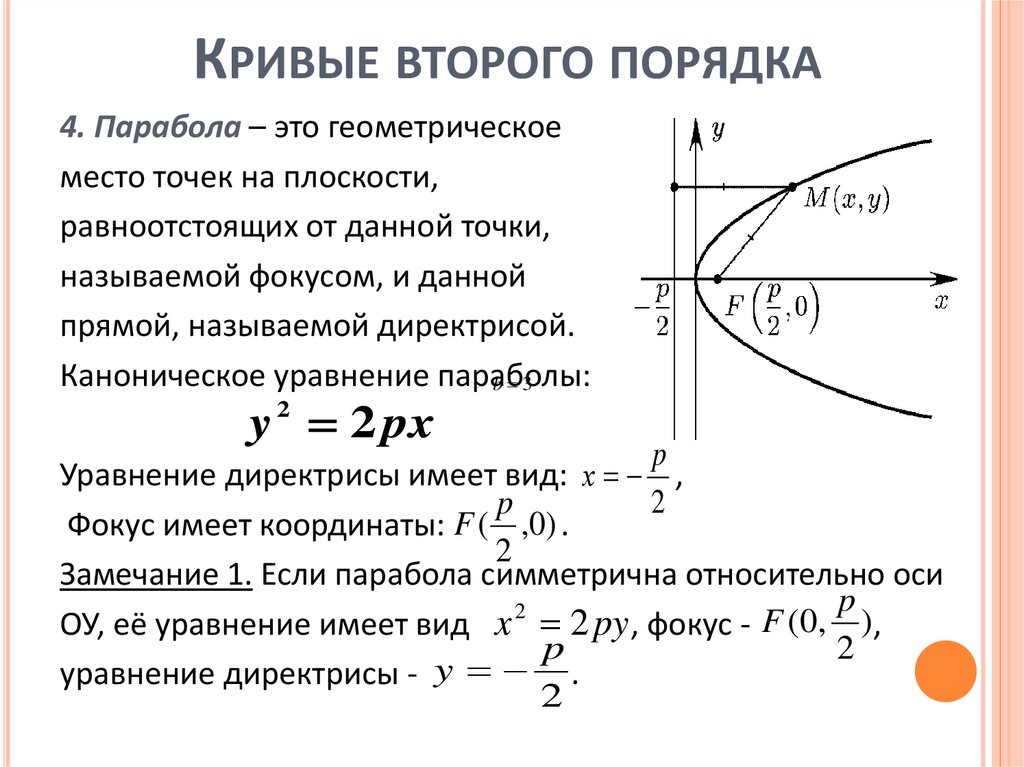
КРИВЫЕ ВТОРОГО ПОРЯДКА
4. Парабола – это геометрическое
место точек на плоскости,
равноотстоящих от данной точки,
называемой фокусом, и данной
прямой, называемой директрисой.
Каноническое уравнение параболы:
b 3
y 2 2 px
p
Уравнение директрисы имеет вид: х ,
2
p
F
(
,
0
)
Фокус имеет координаты:
.
2
Замечание 1. Если парабола симметрична относительно оси
p
2
F
(
0
,
),
ОУ, её уравнение имеет вид x 2 py , фокус 2
p
уравнение директрисы - y .
2

57.

КРИВЫЕ ВТОРОГО ПОРЯДКА
Пример. Определить вид кривой заданной уравнением
9 х 2 25 у 2 36 х 150 у 414 0 .
Найти координаты центра, вершин, фокусов. Сделать рисунок.
Решение. Группируем слагаемые с переменной х и
2
2
переменной у, получим: (9 х 36 х) ( 25 у 150 у) 414 0 .
Из скобок вынесем коэффициенты перед квадратами за скобки:
9( х 2 4 х) 25( у 2 6 у) 414 0 .
В каждой скобке выделим полный квадрат по формуле:
а 2 2ab b 2 (a b) 2 . То есть в первой скобке b 2 ,
в скобке прибавим b 2 4, и столько же вычтем.
2
Во второй скобке b 3 , прибавим b 9 , и столько же вычтем.

58.

КРИВЫЕ ВТОРОГО ПОРЯДКА
Получим:
9 ( х 2) 4 25 ( у 3) 9 414 0;
9 ( х 2 4 х 4) 4 25 ( у 2 6 у 9) 9 414 0;
2
2
9( х 2) 2 36 25( у 3) 2 225 414 0;
9( х 2) 2 25( у 3) 2 225
9( х 2) 2 25( у 3) 2
1;
225
225
( х 2) 2 ( у 3) 2
1;
9
25
( х 2) 2 ( у 3) 2
1.
2
2
3
5
: 225

59.

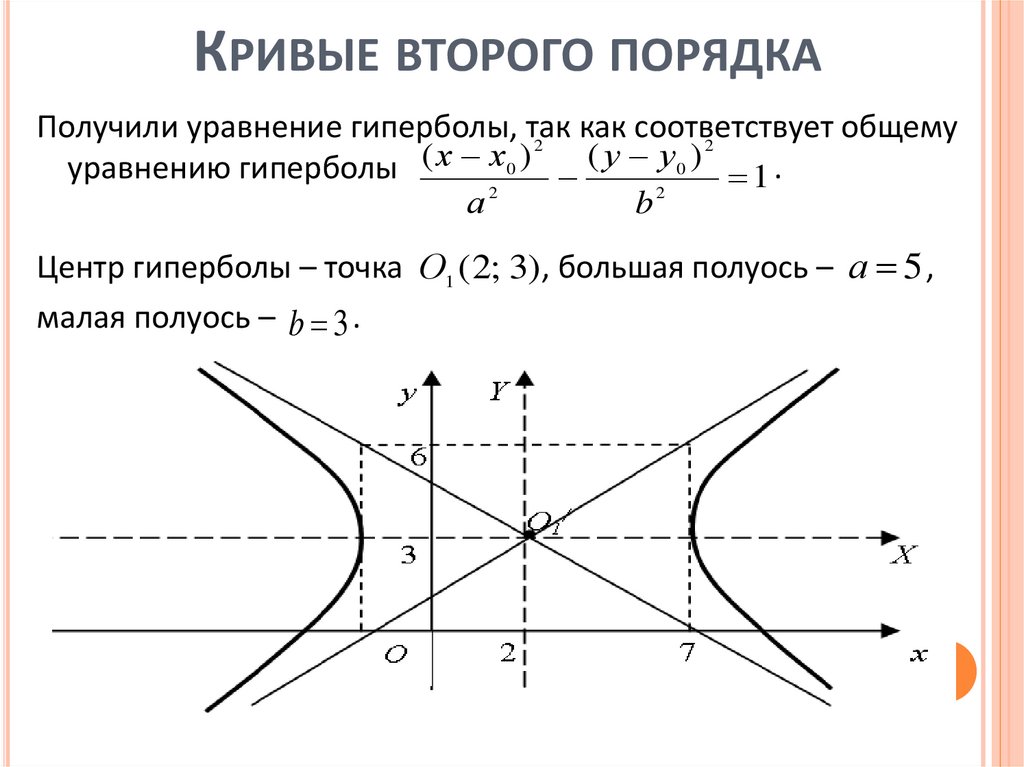
КРИВЫЕ ВТОРОГО ПОРЯДКА
Получили уравнение гиперболы, так
как соответствует
общему
2
2
уравнению гиперболы ( х х0 ) ( у у0 ) 1 .
а2
b2
Центр гиперболы – точка О1 ( 2; 3), большая полуось – а 5 ,
малая полуось – b 3 .

60.

КРИВЫЕ ВТОРОГО ПОРЯДКА
Вершины гиперболы: А1 (7; 3) и А2 ( 3; 3) (точки пересечения
гиперболы с пунктирной ось ОХ). Найдем координаты
фокусов. Для этого воспользуемся условием: b 2 с 2 а 2 (с а)
c 2 a 2 b 2 , c 2 5 2 32 25 9 34, c 34
Тогда, фокусы имеют координаты: F1 (2 34 ; 3) и F2 (2 34 ; 3).

61.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
Уравнение плоскости
Пусть в пространстве R 3 введена прямоугольная система
координат OXYZ. Рассмотрим в пространстве некоторую
плоскость Q. Поверхности Q соответствует некоторое
уравнение F ( x, y, z ) 0 .
Данному уравнению удовлетворяют координаты x, y, z каждой
точки, лежащей на поверхности Q, и не удовлетворяют
координаты никакой точки, не лежащей на ней.
Уравнение F ( x, y, z ) 0 называется уравнением поверхности Q.
1. Общее уравнение плоскости Ах Вy Cz D 0 , где
A 2 B 2 C 2 0.

62.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
2. Уравнение плоскости,
проходящей через точку
M 0 ( x0 , y 0 , z 0 ) с нормальным
вектором n ( A, B, C ):
A( x x0 ) B( y y0 ) C ( z z 0 ) 0
3. Уравнение плоскости в отрезках:
x
y
z
1
a b c

63.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
4. Уравнение плоскости, проходящей через три точки
М 1 ( x1 , y1 , z1 ), М 2 ( x2 , y2 , z 2 ) , М 3 ( x3 , y3 , z3 ).
x x1
x 2 x1
x3 x1
y y1
y 2 y1
y3 y1
z z1
z 2 z1 0
z 3 z1
Пример. Составить уравнение плоскости, проходящей через
три точки М 1 (1,1,1) , М 2 (3,2, 1) , М 3 (4,1,0) .
Решение:
x 1 y 1 z 1
x 1 y 1 z 1
3 1 2 1 1 1 0;
2
1
2 0;
4 1 1 1 0 1
3
0
1

64.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
x 1 y 1 z 1
2
1
2 0;
3
0
1
( х 1) 1 ( 1) 2 0 ( z 1) ( y 1) ( 2) 3 ( z 1) 1 3 ( 2) 0 ( x 1)
2 ( y 1) ( 1) x 1 6 y 6 3z 3 2 y 2 x 4 y 3z 8 0.
Получили уравнение x 4 y 3z 8 0 , умножим обе части
на (-1), получим искомое уравнение плоскости:
x 4 y 3z 8 0

65.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
Прямая и её уравнения в пространстве
1. Общее уравнение прямой (как линия пересечения двух
плоскостей)
Рассмотрим две плоскости:
1 : A1 x B1 y C1 z D1 0
2 : A2 x B2 y C2 z D2 0
A1 x B1 y C1 z D1 0
Тогда, уравнение прямой имеет вид:
A2 x B2 y C 2 z D2 0
2. Канонические уравнения прямой:
x x0
y y0
z z0
l
m
n
Вектор s (l , m, n) - направляющий вектор прямой (вектор,
параллельный данной прямой)

66.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
3. Параметрические уравнения прямой в пространстве:
x x 0 lt
y y 0 mt
z z nt
0
Расстояние от точки до прямой
Пусть дана плоскость Аx By Cz D 0 и точка M 0 ( x0 , y0 , z 0 ) .
Тогда, расстояние от точки до плоскости:
Ax0 By 0 Cz 0 D
d
A2 B 2 C 2
Угол между плоскостями
Пусть заданы две плоскости:
1 : A1 x B1 y C1 z D1 0
2 : A2 x B2 y C2 z D2 0

67.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
Косинус угла между плоскостями определяется по формуле:
cos
A1 A2 B1 B2 C1C2
A1 B1 C1 A2 B2 C2
2
2
2
2
2
2
Угол между прямыми в пространстве
Пусть заданы канонические уравнения двух прямых:
x x1
y y1
z z1
L1 :
l1
m1
n1
L2 :
x x2
y y2
z z2
l2
m2
n2
Косинус угла между прямыми определяется по формуле:
cos
l1l 2 m1m2 n1n2
l1 m1 n1 l 2 m2 n2
2
2
2
2
2
2

68.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
Угол между прямой и плоскостью
Синус острого угла между прямой и плоскостью определяется
по формуле:
sin
Al Bm Cn
l 2 m 2 n 2 A2 B 2 C 2

69.

Пример 1. Составить уравнение плоскости, проходящей через
точку М(-1; 2; 1), перпендикулярно прямой x 5 y z 1
3
4
1
Решение. По уравнению прямой можно определить
координаты
направляющего
вектора
(вектора,
параллельного прямой l), это числа, записанные в
знаменателях уравнения прямой. Это вектор а (3; 4;1)
Так как прямая перпендикулярна
плоскости, поэтому направляющий
вектор прямой будет коллинеарным
к нормальному вектору плоскости,
а значит, они буду иметь одинаковые
координаты.

70.

Таким образом, нормальный вектор плоскости – n (3; 4;1) .
Воспользуемся формулой A( x x0 ) B( y y0 ) C ( z z 0 ) 0 :
3( x ( 1)) 4( y 2) 1( z 1) 0;
3( x 1) 4( y 2) 1( z 1) 0;
3 х 3 4 у 8 z 1 0;
3 x 4 y z 10 0.
Пример 2. а) Найти расстояние от точки М1 до плоскости
(М2 М3 М4); б) Определить угол между прямой (М3 М4) и
плоскостью (М1М2М3), где М1(2; -1; 0), М2(-3; 1; 2), М3(1; 1; -4),
М4(5; 0; 3).
Решение :а) Составим уравнение плоскости (М2 М3 М4):

71.

x 3 y 1 z 2
x 3 y 1 z 2
1 3 1 1 4 2 0; 4
0 6
5 3 0 1 3 2
8
1 1
( х 3) 0 1 ( z 2) 4 ( 1) ( у 1) 8 ( 6) ( z 2) 0 8 ( 1) ( 6) ( x 3)
4 ( y 1) 1 4 z 8 48 y 48 6 x 18 4 y 4 6 x 52 y 4 z 42 0.
Итак, уравнение плоскости имеет вид:
6 x 52 y 4 z 42 0 : ( 2)
3x 26 y 2 z 21 0.
Таким образом, А=3, В=26, С=2, D=-21. Так как точка М1(2; -1; 0)
лежит в плоскости, следовательно, х0=2, у0=-1, z0=0.
Применяем формулу
d
Ax0 By 0 Cz0 D
A2 B 2 C 2

72.

d
3 2 26 ( 1) 2 0 21
32 26 2 2 2
6 26 21
41
9 676 4
689
б) Составим уравнение плоскости (М1 М2 М3):
x 2 y 1 z
x 2 y 1 z
3 2 1 1 2 0; 5
2
2
1 2 1 1 4
1
2 4
( х 2) 2 ( 4) z 2 ( 5) ( у 1) 2 ( 1) z 2 ( 1) 2 2 ( x 2)
( 5) ( y 1) ( 4) 8 х 16 10 z 2 y 2 2 z 4 x 8 20 y 20
12 x 22 y 8 z 2 0 : ( 2)
6 x 11 y 4 z 1 0.
Тогда, А=6, В=11, С=4, D=-1.

73.

Вектор М 3 М 4 будет направляющим вектором прямой (М3 М4).
Найдем координаты этого вектора:
М 3 М 4 5 1; 0 1; 3 ( 4) 4; 1; 7 , т.е. l=4, m=-1, n=7.
Воспользуемся формулой
sin =
Al Bm Cn
l m n A B C
2
2
2
2
6 4 11 ( 1) 4 7
2
2
,
41
41
sin = 2
2
2
2
2
2
66 173
11418
4 ( 1) 7 6 11 4

74.

Математический анализ

75.

ФУНКЦИЯ
Функция – это зависимость между двумя переменными, это
правило, по которому для каждого значения переменной
х можно найти единственное значение переменной у.
Обозначение: y f (x)
х – независимая переменная, аргумент;
у – зависимая переменная, функция.
Все значения независимой переменной х образуют область
определения функции, которая обозначается D(y).
Все значения функции у образуют область значений
функции, которая обозначается Е(у).
х 1
Пример. Найти область определения y
.
2
D( y) : 4 x 2 0 x 2 4 x 2 2 x 2
D( y) ( 2; 2)
4 х

76.

ФУНКЦИЯ
Способы задания функции
1. Табличный способ.
2. Аналитический (с помощью формулы).
3. Графический (с помощью графика).
Виды функций
1. Элементарная функция – это функция, аргументом
которой является переменная х.
2. Сложная функция – это функция, аргументом которой
является другая функция (функция от функции)
Примеры: y=sinx, y=lnx – элементарные функции;
y=cos(2x+4) – сложная функция.

77.

ФУНКЦИЯ
Классы функций
1. Линейная функция – y kx b, график – прямая линия
k
2. Обратная пропорциональность – y , гипербола
x
3. Функция квадратный корень – y x
4. Функция y x 3 , график – кубическая парабола
2
5. Квадратичная функция y ax bx c , парабола
x
6. Показательная функция – y a
7. Логарифмическая функция – y log a x
8. Тригонометрические функции – y sin x , y cos x,
y tgx, y ctgx
9. Обратные тригонометрические функции – y arcsin x,
y arccos x, y arctgx , y arcctgx .

78.

ФУНКЦИИ
Основные свойства функции
1. Нули функции – это значение аргумента, при котором
значение функции равно нулю.
2. Промежутки знакопостоянства - множества значений
аргумента, на которых значения функции только
положительны или только отрицательны.
3. Монотонность функции (возрастание и убывание
функции).
4. Чётность (нечётность) функции.
5. Ограниченность функции.
6. Периодичность функции.

79.

ПРЕДЕЛ ФУНКЦИИ
Число А называется пределом функции f(x) в точке x=a (или в
бесконечно удаленной точке x ) , если при стремлении
аргумента функции к этой точке, значения функции
неограниченно приближаются к числу A.
Обозначение:
lim f ( x) A
lim f ( x) A
x x0
x
Свойства пределов
Пусть
lim f ( x)
x
и
lim g ( x)
x
существуют
1. lim( f ( x) g ( x)) lim f ( x) lim g ( x)
x
x
x
f ( x) g ( x)) lim f ( x) lim g ( x)
2. lim(
x
x
x
f ( x)
f ( x ) lim
x
lim
3. x
g ( x)
lim g ( x )
x

80.

ПРЕДЕЛ ФУНКЦИИ
Раскрытие неопределённостей
Иногда правила предельного перехода непосредственно
0
неприменимы, так как возникают ситуации ,
,
,
0
Такие ситуации получили название – неопределённость.
Примеры:
1
x2 1 0
( x 1)( x 1)
x 1
2
lim
lim 2
1. lim
2
x 1 x 3 1
x
1
x
1
( x 1)( x x 1)
x x 1 3
0
x 4 2 0
( x 4 2)( x 4 2)
x 4 4
2. lim
=
lim
lim
x 0
x
0
x
0
x
x( x 4 2)
x( x 4 2)
0
x
1
1
lim
= lim
x 0
x( x 4 2) x 0 x 4 2 4
(домножение на сопряжённое)

81.

ПРЕДЕЛ ФУНКЦИИ
1
1
1
1
(
3 ) lim (
)
3. lim
2
x 1 x 1
x 1 x 1
x 1
( x 1)( x x 1)
.
x2 x 1 1
x2 x 2
lim
lim 3
3
x 1
x 1 x 1
x 1
0

82.

ПРЕДЕЛ ФУНКЦИИ
Замечательные пределы
sin x
Первый замечательный предел lim
,
1
x 0
x
1 x
Второй замечательный предел lim(1 ) e.
x
x
Примеры:
sin 5 x
5 sin 5 x
sin 5 x
lim
5 lim
5 1 5
5. lim
x 0
x 0
x 0
x
5x
5x
1
6. lim (1 ) x. Положим x y, при х , у
x
x
1 y
1
1
1
lim (1 ) lim
y
y
1 y
1 y e
y
(1 )
lim (1 )
y
y
y

83.

ПРЕДЕЛ ФУНКЦИИ
2х 3
7. lim
х
2
х
1
х 1
5х
2х 1 4
lim
х
2
х
1
1
lim 1
х
2х 1
4
e
lim
4 x 4
х 10 x 2 5 x
2 х 1 4 х 1
4 2 х 1 5 х
e0 1
х 1
5х
4
1
1
lim
1
lim
х
х
2х 1
2х 1
4
4 х 1
1
lim 1
х
2х 1
4
х 1
5х
2 х 1
4
х 1
5х
2 х 1 5 х
e
4 х 1
х 2 х 1 5 х
lim

84.

ПРЕДЕЛ ФУНКЦИИ
Сравнение бесконечно малых
бесконечно малые (последовательности или
Пусть и
функции).
1) Если конечный и отличный от нуля предел существует
lim C , C 0, C ,
то и являются бесконечно малыми (б.м.) одного и того
же порядка.
2) Если lim
, то имеет высший порядок малости по
0
отношению к (или - б.м. более высокого порядка,
чем ).

85.

ПРЕДЕЛ ФУНКЦИИ
, то имеет высший порядок малости по
отношению к (или - б.м. более высокого порядка, чем ).
3) Если lim
4) Если lim 1, то бесконечно малые и называются
эквивалентными.
Таблица эквивалентных бесконечно малых при x 0
x
6. log a ( x 1) ~
1. sin x ~ x
lna
2. tgx ~ x
7. ln( x 1) ~ x
3. arcsin x ~ x
8. a x 1 ~ xlna
4. arctgx ~ x
9. e x 1 ~ x
x2
5. 1 cos x ~
2
10. x 1 1 ~
x
2

86.

ПРЕДЕЛ ФУНКЦИИ
Примеры:
arcsin(3 x 2 ) (e 2 x 1)
3x 2 2 x
6 x 3 12
lim
lim
.
2
3
1. lim
x 0
x 0 5 x
(cos x 1)arctg (sin 5 x) x 0 x
5
5x
2
2
4x 2 1
(2 x 1)( 2 x 1)
(2 x 1)( 2 x 1)
0
lim
lim
2. lim1
1
1
2x 1
x arcsin( 2 x 1)
0 x arcsin( 2 x 1) x
2
2
lim ( 2 x 1) 2
x
1
2
2

87.

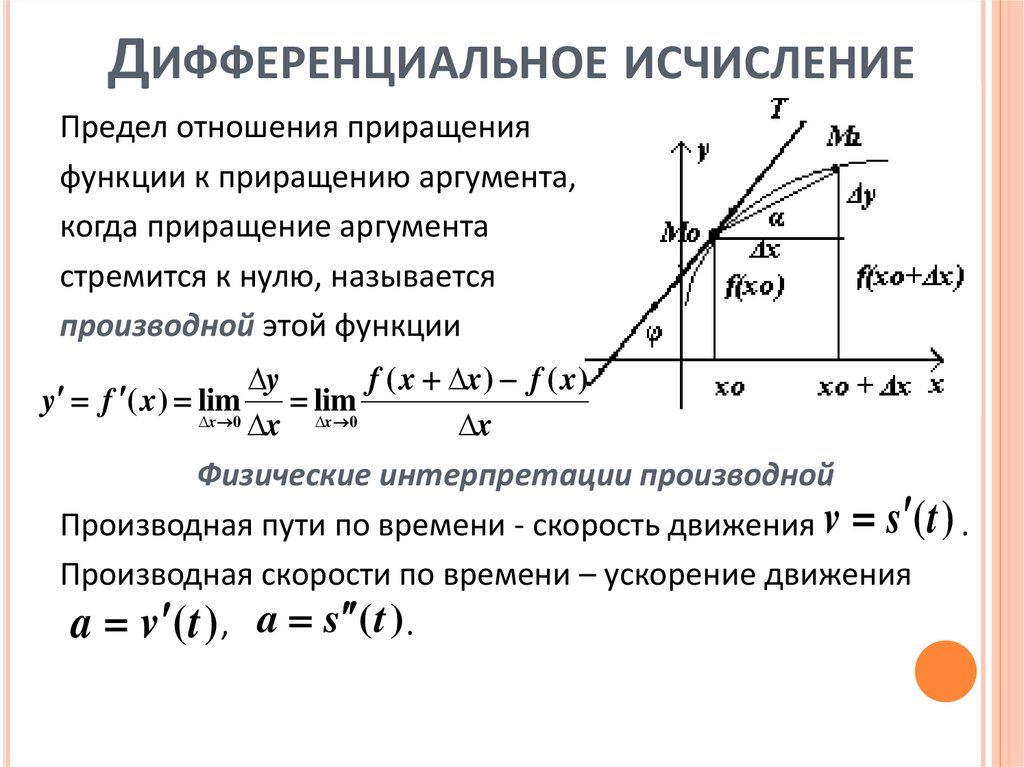
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Предел отношения приращения
функции к приращению аргумента,
когда приращение аргумента
стремится к нулю, называется
производной этой функции
y
f ( x x ) f ( x )
lim
x 0
x x 0
x
y f ( x ) lim
Физические интерпретации производной
Производная пути по времени - скорость движения v s (t ) .
Производная скорости по времени – ускорение движения
a v (t ) , a s (t ) .

88.

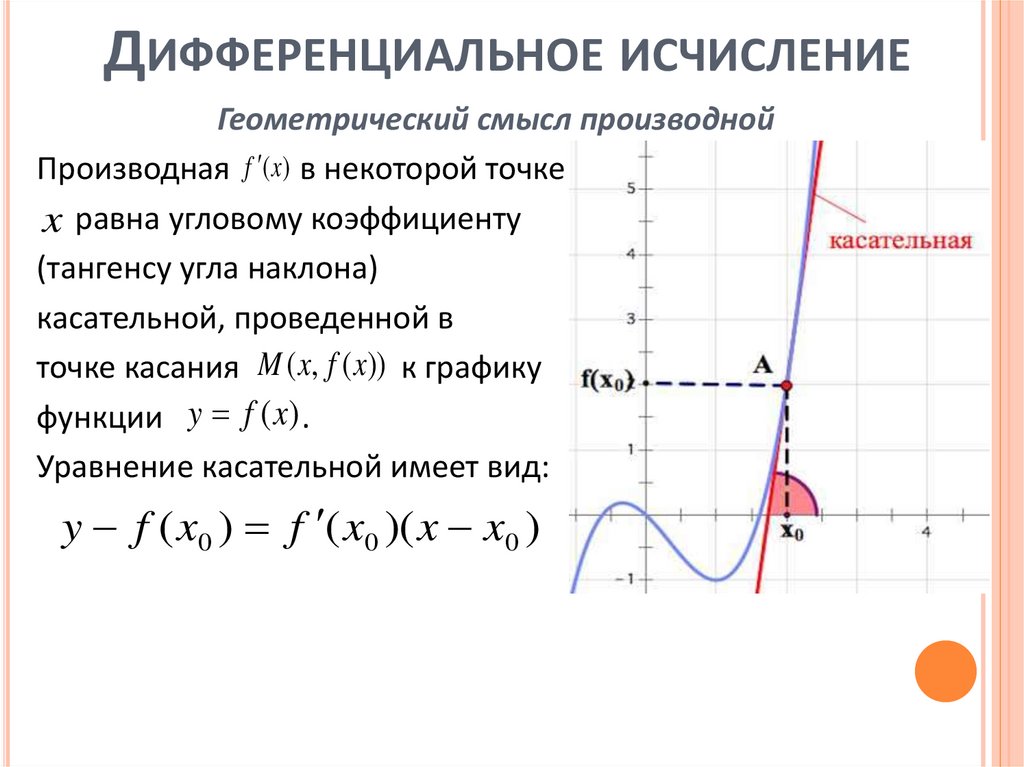
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Геометрический смысл производной
Производная f (x) в некоторой точке
x равна угловому коэффициенту
(тангенсу угла наклона)
касательной, проведенной в
точке касания M ( x, f ( x)) к графику
функции y f (x) .
Уравнение касательной имеет вид:
y f ( x0 ) f ( x0 )( x x0 )

89.

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Правила дифференцирования
1. (Сu ) Cu
2. (u v ... w) u v ... w
3. (uv ) u v uv
u
u v uv
( v 0)
4. ( )
2
v
v
5.
Производная сложной функции по независимой
переменной равна производной заданной функции по
промежуточному аргументу, умноженной на производную
промежуточного аргумента по независимой переменной
y x yu u x

90.

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Таблица производных основных функций

91.

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Таблица производных основных функций

92.

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Примеры:
3
2
3
1. y 5 x cos x x x 17
2
3
1
2 3
3
3
2
3 2
y (5 x cos x x x 17) (5 x cos x x x 17) 15 x sin x x 1
3
15 x sin x
2
2
3
3 x
2. y
sin( 4 x)
y
1
2 sin( 4 x)
1.
cos( 4 x) 4
2 cos( 4 x)
sin( 4 x) .
Дифференциал функции dy y x или df ( x) f ( x) x

93.

ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИИ
1. Исследование функции на монотонность
Теорема (признак возрастания и убывания функции). Если
функция y f (x) дифференцируема во всех точках какого-то
интервала и ее производная f (x ) положительна в каждой
точке, то функция возрастает на этом интервале. Если
производная f (x ) отрицательна, то функция убывает.
3
2
Пример. Исследовать функцию y x 9 x 15 x 7 на
монотонность.
3
2
2
Решение: y ( x 9 x 15 x 7) 3x 18x 15,
y 0, 3x 2 18x 15 0, x 2 6 x 5 0, x 1, x 5
y 0 при х ( ;1) (5; ), следовательно, f (x) возрас.
y 0 при х (1;5), следовательно, функция убывает

94.

ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИИ
2. Исследование функции на экстремумы
Теорема (необходимый признак экстремума, признак
Ферма). Если в точке экстремума x 0
функция имеет
производную, то производная равна нулю.
Теорема (достаточный признак экстремума). Если при
переходе через стационарную точку x 0 (движение слева
направо) производная меняет знак с «+» на «–», то точка x 0
точка максимума, если же с «–» на «+», то x 0 - точка
минимума.
Пример. В предыдущем примере точка x 1 - точка
максимума, точка x 5 - точка минимума.

95.

ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИИ
3. Наименьшее и наибольшее значения функции на отрезке
Правило отыскания наибольших и наименьших значений:
1) находим производную исследуемой функции f (x) ;
2) определяем критические точки (решаем уравнение f ( x) 0);
3) вычисляем значения функции в критических точках и концах
интервала;
4) отбираем среди вычисленных значений самое большое и
самое малое.
Пример. Найти наибольшее и наименьшее значение функции
x 3 5x 2
y
6 x 1 на отрезке [0,10].
3
2

96.

ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ
y x 2 5 x 6;
2
2) y 0 : x 5x 6 0, x1 2, x2 3. Получили две критические
Решение: 1)
точки.
3) составим таблицу значений в критических точках и в концах
интервала:
x
0
y
-1
2
3
2
3
1
4) наибольшее значение 142
3
3
10
7
2
142
1
3
достигается в правом конце
интервала х=10, наименьшее значение (-1) в левом конце
интервала х=0.

97.

ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ
4. Выпуклость, вогнутость и точки перегиба кривой
Теорема. Если функция y f (x) дважды дифференцируема
во всех точках какого-то интервала и ее вторая
производная f (x) положительна в каждой точке, то это
является признаком выпуклости кривой. Если вторая
производная f (x) отрицательна, то кривая вогнута.
Теорема (необходимый признак точки перегиба). Если точка
M ( x0 , f ( x0 )) точка перегиба, то либо f ( x0 ) 0, либо не
существует
Теорема (достаточный признак точки перегиба). Если при
переходе через точку x 0 вторая производная функции
меняет знак, то x 0 - точка перегиба.

98.

ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ
Пример. Исследовать функцию на выпуклость, вогнутость,
точки перегиба: у х 3 3х 2 8х 5.
Решение:
2
1) у 3х 6 х 8;
2) у 6 х 6;
3) у 0;
6 х 6 0;
х 1
х 1- точка перегиба. На интервал е ( ; 1) кривая является
вогнутой, на интервале (1; ) - выпуклой.

99.

ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ
5. Асимптоты графика функции
Прямая L называется асимптотой кривой, если расстояние
от текущей точки М на кривой до прямой L становится
бесконечно малой величиной, когда точка М
неограниченно удаляется от начала координат (т.е. когда
расстояние от М до начала координат ).
Виды асимптот:
1. Вертикальные асимптоты могут образовываться только в
точках бесконечного разрыва функции y f (x) .
2. Наклонные асимптоты. Уравнение наклонной асимптоты к
кривой y f (x) имеет вид:
f ( x)
y kx b, k lim
, b lim ( f ( x) kx)
x
x
x

100.

ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ
x3 2
Пример. Найти асимптоты линии y 2
.
x 4
Решение: 1) Знаменатель дроби обращается в нуль в точках:
x 2 4 0, x1 2, x2 2 . Проверим, будут ли вертикальные
прямые x 2, x 2 асимптотами:
x3 2
x3 2
x3 2
x3 2
lim
, lim 2
, lim 2
, lim 2
x 2 0 x 2 4
x 2 0 x 4
x 2 0 x 4
x 2 0 x 4
Таким образом, прямые x 2, x 2 - вертикальные асимпт.
2)Найдём наклонные асимптоты:
y kx b,
2
1 3
f ( x)
x3 2
x 1;
k lim
lim 3
lim
x
x x 4 x
x
4
x
1 2
x

101.

ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ
x3 2
x3 2 x3 4x
b lim
( f ( x) kx ) lim
( 2
1 x) lim
2
x
x
x
x 4
x 4
4 2
2
4x 2
x x 0
lim
lim
x
x 2 4 x 1 4
x2
Таким образом, уравнение наклонной асимптоты
y x.

102.

ПРАВИЛО ЛОПИТАЛЯ
( x)
Отыскивается lim
при x 0 или x , когда
( x)
( x) 0
( x) . Если
одновременно
или
(
x
)
0
( x)
существует предел (конечный или бесконечный) отношения
( x)
производных lim
, то существует и предел отношения
( x)
( x)
( x)
функций и эти пределы равны: lim
.
lim
( x)
( x)
Пример.
sin 7 x
(sin 7 x)
7 cos 7 x 7
lim
lim
lim
.
x 0 sin 3 x
x 0 (sin 3 x )
x 0 3 cos 3 x
3

103.

ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
1. Элементарное исследование: область определения; точки
разрыва и интервалы непрерывности; точки пересечения
графика с осями координат; симметрия графика: четность,
нечетность; вертикальные и наклонные асимптоты.
2. Исследование на возрастание, убывание и точки экстремума
с помощью производной функции.
3. Выпуклость, вогнутость
второй производной.
4. Построение графика
и точки перегиба – с помощью

104.

СПАСИБО ЗА ВНИМАНИЕ