Углы между прямыми и плоскостями

1.

Углы между прямыми и
плоскостями.
Угол между скрещивающимися прямыми. Угол между
прямой и плоскостью. Угол между плоскостями. Площадь
ортогональной проекции многоугольника

2.

Угол между прямой и плоскостью
Угол между прямой и плоскостью – это угол между прямой и её
проекцией на эту плоскость.
Геометрический метод нахождения угла между прямой и плоскостью
При геометрическом методе нужно найти какую-нибудь удобную точку
на прямой, опустить перпендикуляр на плоскость, выяснить, что из себя
представляет проекция, а потом решать планиметрическую задачу по
поиску угла (φ) в треугольнике (зачастую прямоугольном).
Алгебраический метод нахождения угла между прямой и плоскостью
При алгебраическом методе вводится система координат,
определяются координаты двух точек на прямой и уравнение
плоскости, а затем применяется формула вычисления угла между
прямой и плоскостью.

3.

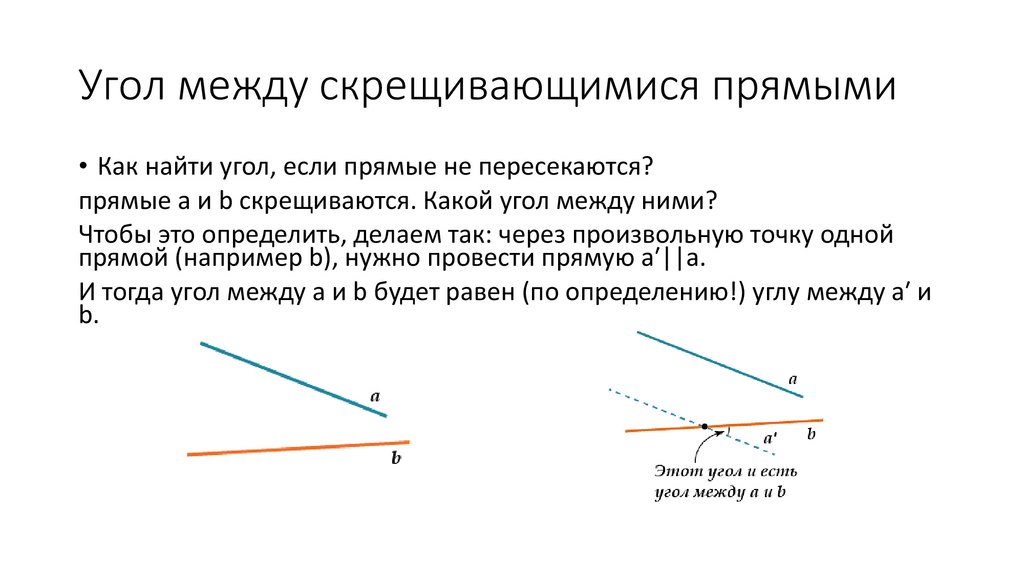
Угол между скрещивающимися прямыми
• Как найти угол, если прямые не пересекаются?
прямые a и b скрещиваются. Какой угол между ними?
Чтобы это определить, делаем так: через произвольную точку одной
прямой (например b), нужно провести прямую a′||a.
И тогда угол между a и b будет равен (по определению!) углу между a′ и
b.

4.

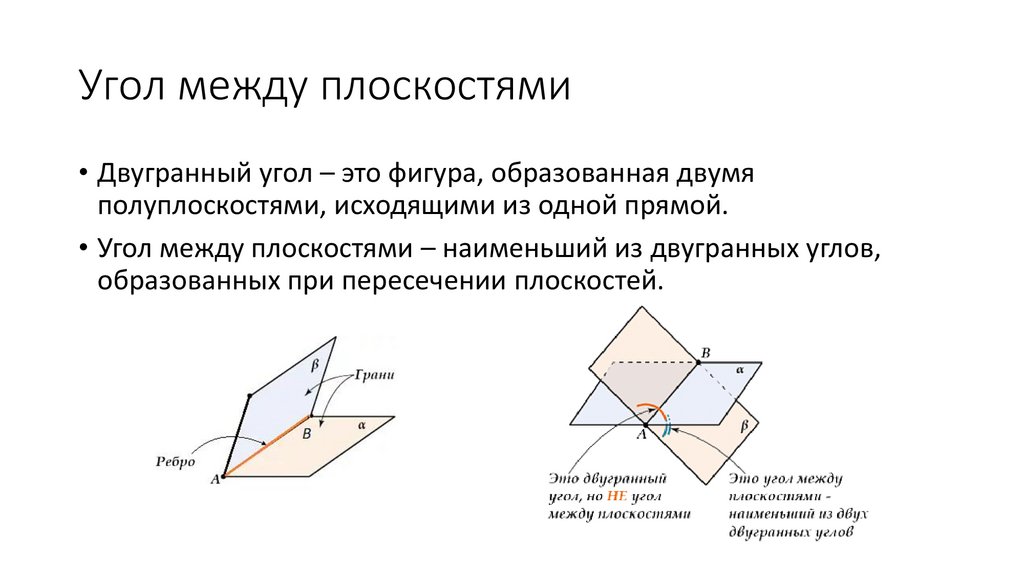
Угол между плоскостями
• Двугранный угол – это фигура, образованная двумя
полуплоскостями, исходящими из одной прямой.
• Угол между плоскостями – наименьший из двугранных углов,
образованных при пересечении плоскостей.

5.

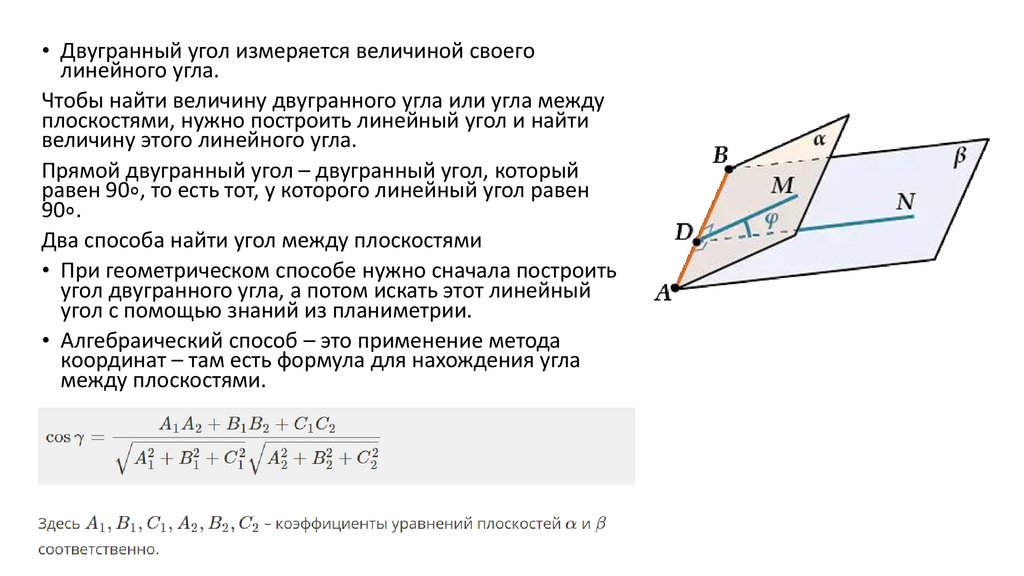
• Двугранный угол измеряется величиной своего
линейного угла.
Чтобы найти величину двугранного угла или угла между
плоскостями, нужно построить линейный угол и найти
величину этого линейного угла.
Прямой двугранный угол – двугранный угол, который
равен 90∘, то есть тот, у которого линейный угол равен
90∘.
Два способа найти угол между плоскостями
• При геометрическом способе нужно сначала построить
угол двугранного угла, а потом искать этот линейный
угол с помощью знаний из планиметрии.
• Алгебраический способ – это применение метода
координат – там есть формула для нахождения угла
между плоскостями.

6.

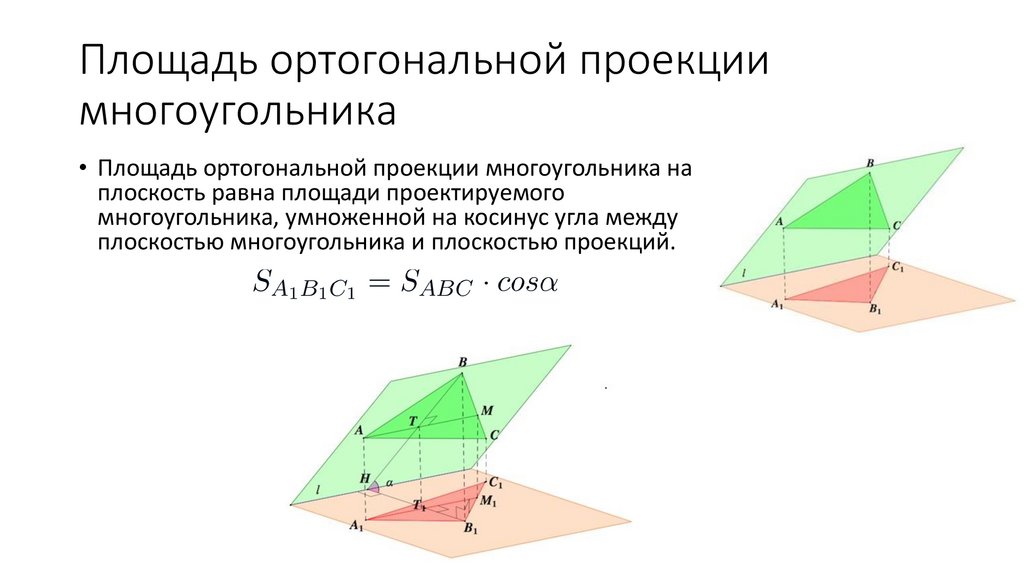
Площадь ортогональной проекции
многоугольника
• Площадь ортогональной проекции многоугольника на
плоскость равна площади проектируемого
многоугольника, умноженной на косинус угла между
плоскостью многоугольника и плоскостью проекций.

7.

Пример