Похожие презентации:
Признаки равенства прямоугольных треугольников
1.
Признаки равенствапрямоугольных
треугольников
2.
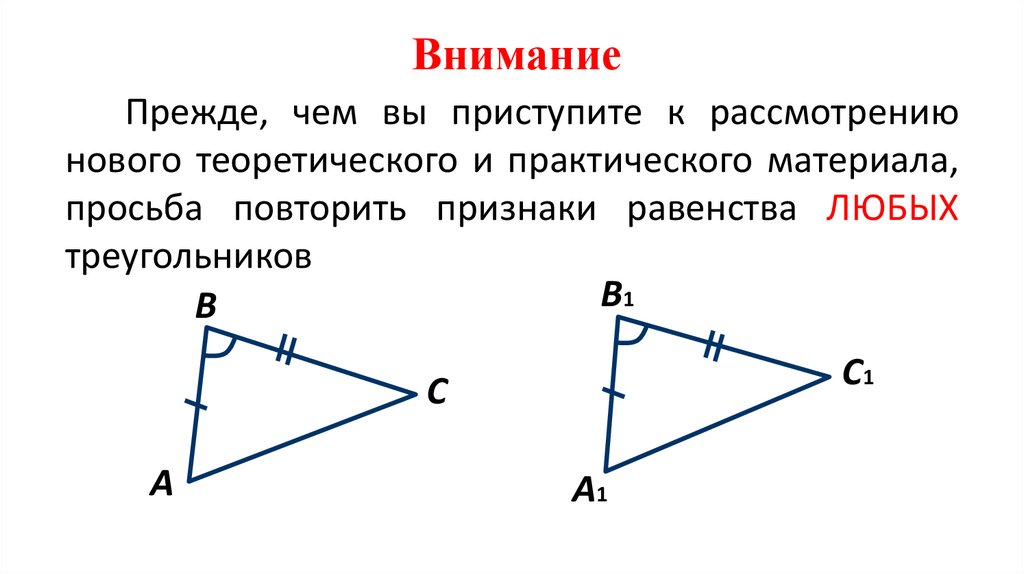
ВниманиеПрежде, чем вы приступите к рассмотрению
нового теоретического и практического материала,
просьба повторить признаки равенства ЛЮБЫХ
треугольников
В1
В
С1
С
А
А1
3.
Первый признак равенства треугольниковЕсли две стороны и угол между ними одного
треугольника соответственно равны двум сторонам
и углу между ними другого треугольника, то такие
треугольники равны.
В1
В
С1
С
А
А1
4.
Второй признак равенства треугольниковЕсли сторона и два прилежащих к ней угла одного
треугольника соответственно равны стороне и двум
прилежащим к ней углам другого треугольника, то
такие треугольники равны.
В1
В
С1
С
А
А1
5.
ВниманиеТак как в прямоугольных треугольниках уже
есть один равный элемент- прямой угол, то
формулировка признаков равенства
треугольников меняется.
В тетрадь записываем ТОЛЬКО формулировки
теорем с рисунком ( без доказательств).
6.
Теорема (о равенстве прямоугольных треугольниковпо двум катетам)
Если катеты одного прямоугольного треугольника
соответственно равны катетам другого прямоугольного
треугольника, то такие треугольники равны.
А1
А
Доказательство.
АС = А1С1, ВС = В1С1,
∠ С = ∠ С1 = 90°.
Получаем, что ∆ АВС = ∆ А1В1С1
(по первому признаку). С
Теорема доказана.
В С1
В1
7.
Теорема (о равенстве прямоугольных треугольниковпо катету и прилежащему острому углу)
Если катет и прилежащий к нему острый угол одного
прямоугольного треугольника соответственно равны
катету и прилежащему к нему острому углу другого
прямоугольного треугольника, то такие треугольники
А
А1
равны.
Доказательство.
АС = А1С1, ∠ А = ∠ А1,
∠ С = ∠ С1 = 90°.
Получаем, что ∆ АВС = ∆ А1В1С1
(по второму признаку).
Теорема доказана.
С
В С1
В1
8.
Теорема (о равенстве прямоугольных треугольниковпо гипотенузе и острому углу)
Если гипотенуза и острый угол одного прямоугольного
треугольника соответственно равны гипотенузе и острому
углу другого прямоугольного треугольника, то такие
треугольники равны.
Доказательство.
А
А1
∠ С = ∠ С1 = 90°, АВ = А1В1, ∠ А = ∠ А1.
∠ А + ∠ В = 90°, ∠ А1 + ∠ В1 = 90°,
∠ В = 90° – ∠ А, ∠ В1 = 90° – ∠ А1, ∠ В = ∠ В1.
Следовательно, ∆ АВС = ∆ А1В1С1
С
(по второму признаку).
Теорема доказана.
В С1
В1
9.
Теорема (о равенстве прямоугольных треугольниковпо гипотенузе и катету)
Если гипотенуза и катет одного прямоугольного
треугольника соответственно равны гипотенузе и
катету другого прямоугольного треугольника, то такие
треугольники равны.
А
(А1)
Доказательство.
∠ С = ∠ С1 = 90°, АВ = А1В1, АС = А1С1.
∆ В1АВ – равнобедренный,
АС – высота, медиана.
В
То есть В1С = СВ.
Следовательно, ∆ АВС = ∆ А1В1С1
(по двум катетам).
Теорема доказана.
С
(С1)
В1
10.
Задача 1. ( пишем в тетрадь) На рисунке отрезки СА иDB перпендикулярны прямой АВ, отрезок ОА равен
отрезку ОВ. Докажите, что отрезок СА равен отрезку DB.
Доказательство.
D
∆ АСО, ∆ BDO – прямоугольные.
АО = ОВ,
∠ АОС = ∠ ВОD (как вертикальные). А
Тогда ∆ АСО = ∆ BDO
(по катету и острому углу).
С
Откуда СА = DВ.
O
В
11.
Задача 1. ( пишем в тетрадь) На рисунке отрезки СА иDB перпендикулярны прямой АВ, отрезок ОА равен
отрезку ОВ. Докажите, что отрезок СА равен отрезку DB.
Доказательство.
D
∆ АСО, ∆ BDO – прямоугольные.
1)АО = ОВ( по условию),
2)∠ АОС = ∠ ВОD (как вертикальные).А
Тогда ∆ АСО = ∆ BDO
(по катету и острому углу).
С
Откуда СА = DВ.
O
В
12.
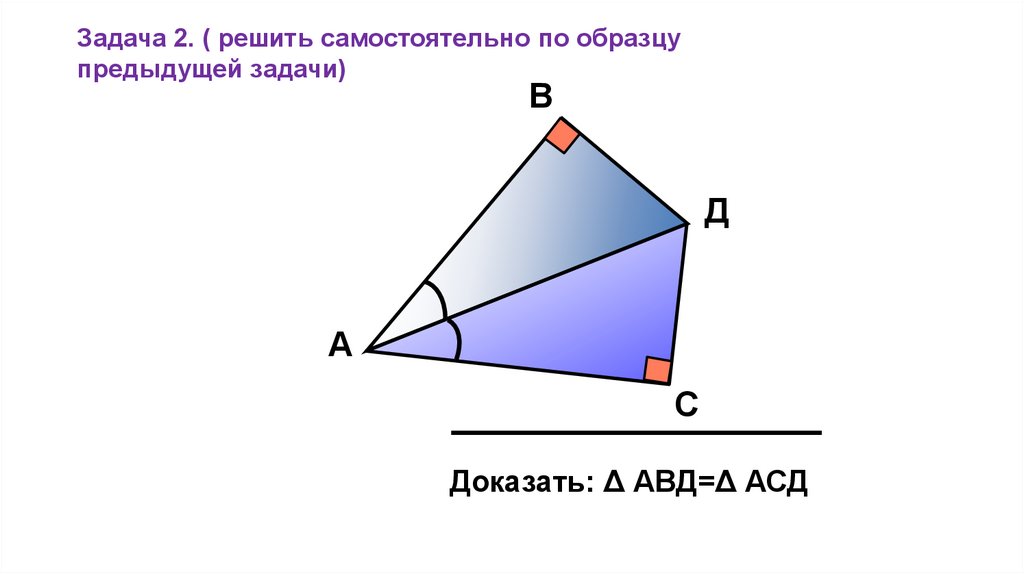
Задача 2. ( решить самостоятельно по образцупредыдущей задачи)
В
Д
А
С
Доказать: Δ АВД=Δ АСД
13.
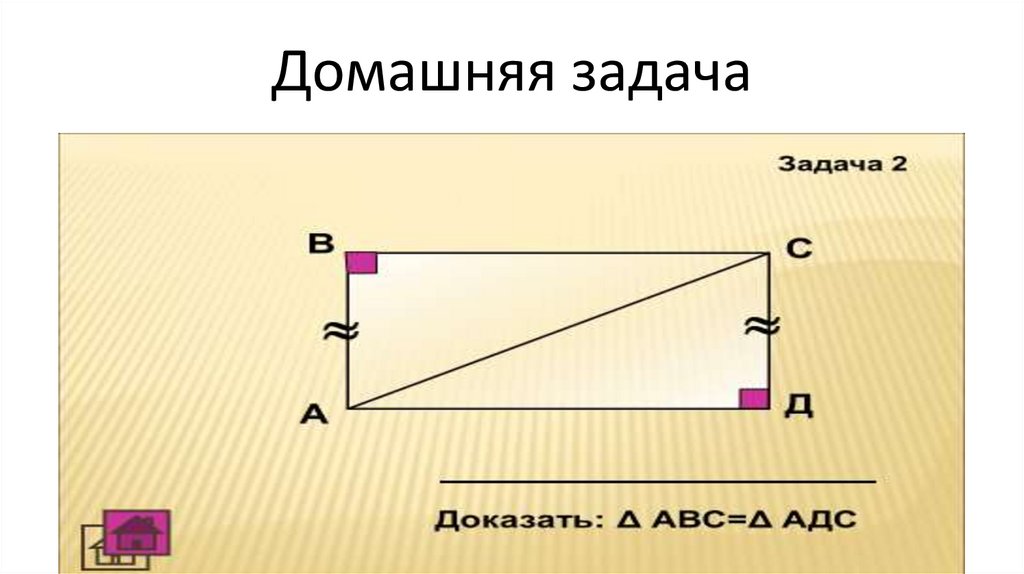
Домашняя работа• Выучить признаки равенства
прямоугольных треугольников.
• Решить задачу по готовому рисунку
(смотрите следующий слайд).











 Математика
Математика








