Похожие презентации:
Кручение. Занятие 24
1.
КручениеВнутренние силовые факторы при кручении
Построение эпюр крутящих моментов
Кручение - вид нагружения, при котором в
поперечном сечении бруса возникает только один
внутренний силовой фактор - крутящий момент.
Эпюра крутящего момента - график
распределения крутящего момента вдоль оси бруса
по сечениям.
1
2.
Кручение круглого брусапроисходит
при
нагружении его парами сил
с моментами в плоскостях,
перпендикулярных
продольной оси (рис. 1).
Длина бруса и размеры
поперечного сечения при
кручении не изменяются.
Образующие
бруса
искривляются
и
разворачиваются на угол γ - угол сдвига (угол
поворота образующей)
Поперечные сечения разворачиваются на угол φ угол закручивания (угол поворота сечения).
2
3.
34.
Гипотезы при кручении1. Гипотеза плоских сечений - поперечное
сечение бруса, плоское и перпендикулярное
продольной оси, после деформации остается
плоским и перпендикулярным продольной оси.
2. Радиус, проведенный из центра поперечного
сечения бруса, после деформации остается прямой
линией (не искривляется).
3. Расстояние между поперечными сечениями
после деформации не меняется. Ось бруса не
искривляется, диаметры поперечных сечений не
меняются.
4
5.
56.
А - площадь сечения;dA - элементарная площадка;
Q - поперечная сила действующая на всё
сечение;
dQ - поперечная сила действующая на
элементарную площадку;
p - расстояние от элементарной площадки до
центра круга;
R - радиус сечения; D - диаметр сечения;
Mк - момент сил упругости действующих на всё
сечение;
dM - момент сил упругости действующих на
элементарную площадку;
6
τ - касательное напряжение;
7.
Внешними нагрузками являются две противоположнонаправленные пары сил.
Рассечем брус плоскостью I и рассмотрим равновесие
отсеченной части.
Сечение рассматриваем со стороны отброшенной
части.
Внешний момент пары сил разворачивает участок
бруса против часовой стрелки, внутренние силы
упругости сопротивляются повороту. В каждой точке
сечения возникает поперечная сила dQ.
Каждая точка сечения имеет симметричную, где
возникает поперечная сила, направленная в обратную
сторону.
Эти силы образуют пару с моментом dM = p∙dQ;
р - расстояние от точки до центра сечения.
Сумма поперечных сил в сечении равна нулю ∑dQ = 0.7
8.
89.
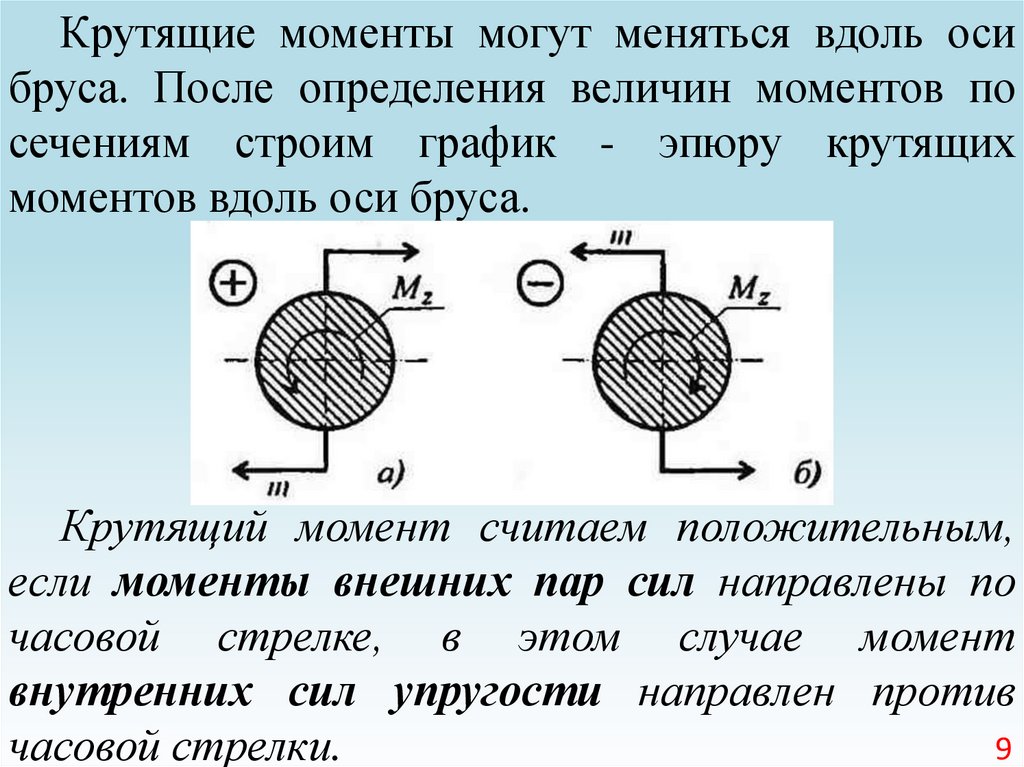
Крутящие моменты могут меняться вдоль осибруса. После определения величин моментов по
сечениям строим график - эпюру крутящих
моментов вдоль оси бруса.
Крутящий момент считаем положительным,
если моменты внешних пар сил направлены по
часовой стрелке, в этом случае момент
внутренних сил упругости направлен против
9
часовой стрелки.
10.
Напряжения и деформации при кручении10
11.
Проводим на поверхности бруса сетку изпродольных и поперечных линий. Рассмотрим
элемент бруса 1234 после деформации.
Используем закон Гука при сдвиге и гипотезы
плоских сечений и неискривления радиусов
поперечных (прямоугольники превращаются в
параллелограммы)
При
кручении
возникает
напряженное
состояние, называемое «чистый сдвиг» (рис. б).
При сдвиге на боковой поверхности элемента
1234 возникают касательные напряжения, равные
по величине (рис. в), элемент деформируется (рис.
в).
11
12.
Материал подчиняется закону Гука.Касательное напряжение пропорционально углу
сдвига.
Закон Гука при сдвиге
τ=G∙γ;
где G - модуль упругости при сдвиге, Н/мм2;
γ - угол сдвига, рад.
12
13.
1314.
1415.
Касательное напряжение при кручениипропорционально расстоянию от точки до
центра сечения.
Jp - полярный моментом инерции сечения
Эпюра распределения касательных напряжений
при кручении (рис. 5)
Мк - крутящий момент в сечении;
pB - расстояние от точки В до центра;
τB - напряжение в точке B;
15
τк max - максимальное напряжение.
16.
1617.
1718.
1819.
1920.
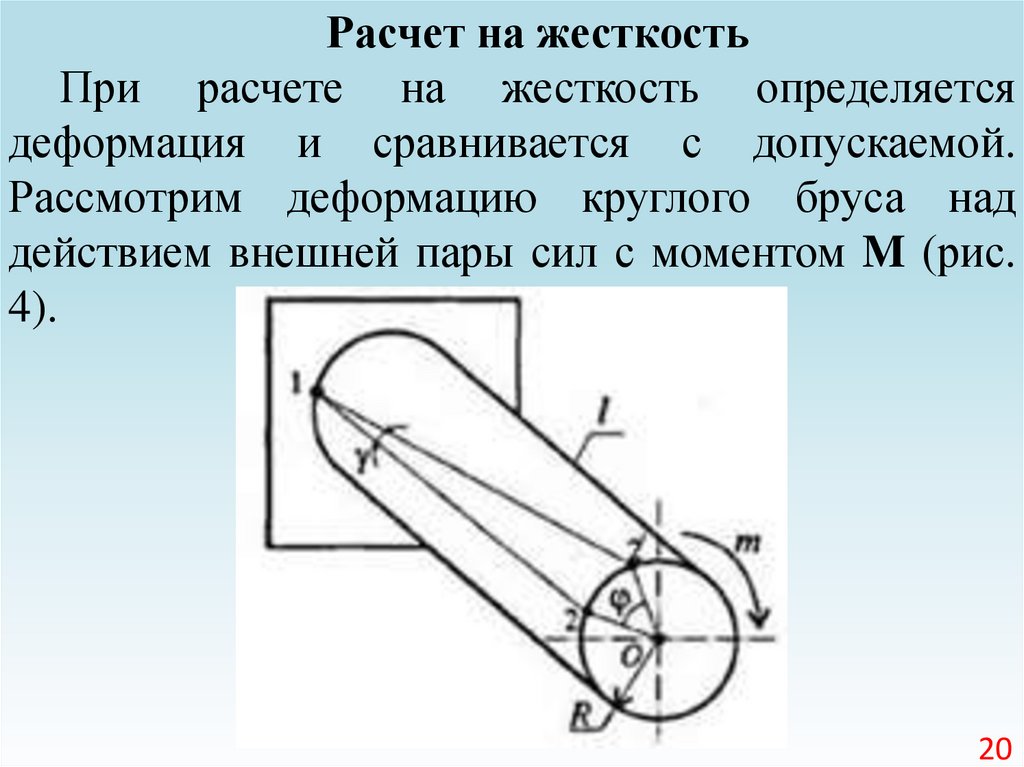
Расчет на жесткостьПри расчете на жесткость определяется
деформация и сравнивается с допускаемой.
Рассмотрим деформацию круглого бруса над
действием внешней пары сил с моментом M (рис.
4).
20





















 Механика
Механика








