Функции, основные свойства функций

1. Функции, основные свойства функций

2.

Галилео Галилей
(1564-1642)
Итальянский физик,
астроном, математик
однажды заметил:
«книга природы
написана на
математическом
языке», а именно
функция позволяет
описывать процессы
движения, изменения,
присущие природе.

3.

Понятие функции
У
Х
Х
f(x)
У
х – независимая переменная, аргумент
у – зависимая переменная, результат,
функция.

4. Понятие функции

Зависимости одной переменной
от другой называются
функциональными
зависимостями.
Зависимость переменной y от
переменной x называется
функцией, если каждому
значению x соответствует
единственное значение y.

5.

При этом используют запись
y=f(x).
Переменную x называют
независимой переменной или
аргументом, а переменную y зависимой переменной.
.

6.

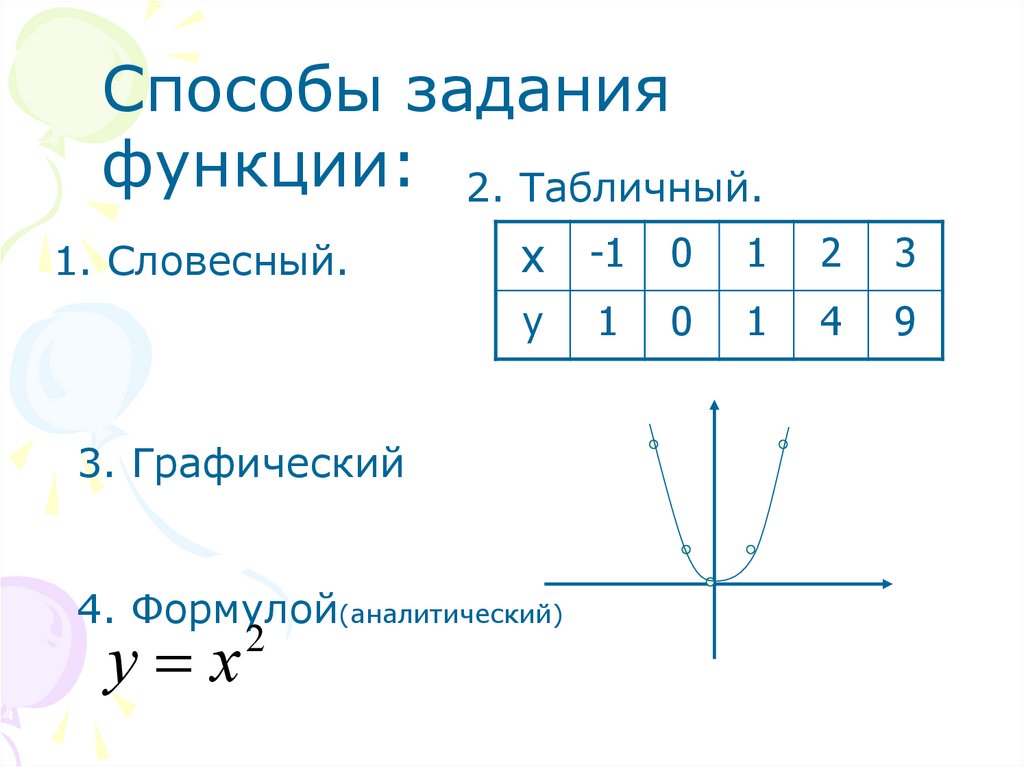
Способы задания
функции: 2. Табличный.
1. Словесный.
х -1 0
1
2
3
у
1
4
9
3. Графический
4. Формулой(аналитический)
2
у х
1
0

7.

Область определения
функции
(ООФ)
Областью определения функции называют
множество всех значений, которые может
принимать ее аргумент х
Обозначается
D(х)

8.

Область определения
функции
у 4х 3
2
у 2 х 3х 5
2
у
х 1
у 2х 6
Все действительные
числа
Все действительные
числа
Х+1≠0 ⇒ Х≠-1
2х-6≥0 ⇒ 2х≥6 ⇒

9.

Множество значений
функции
(ОДЗ)
Множеством значений функции
называют множество всех значений
которые может принимать
переменная у
Обозначается
Е(у)

10.

Множество значений
функции
у 4х 3
у х
Все действительные
числа
2
у≥0
1
у
х
у≠0
у
у≥0
х

11.

x1
x2 x1
f ( x2 ) f ( x1 )
x2

12.

y
1
0
1
x
1
x
y
1
0

13.

x1
x2 x1
f ( x2 ) f ( x1 )
x2

14.

y
y
0 1
x
1
0 1
x

15.

Функция, только
возрастающая или только
убывающая на данном
числовом промежутке,
называется монотонной
на этом промежутке.
y
y
1
0
1
x
1
0 1
x

16.

17.

18.

19.

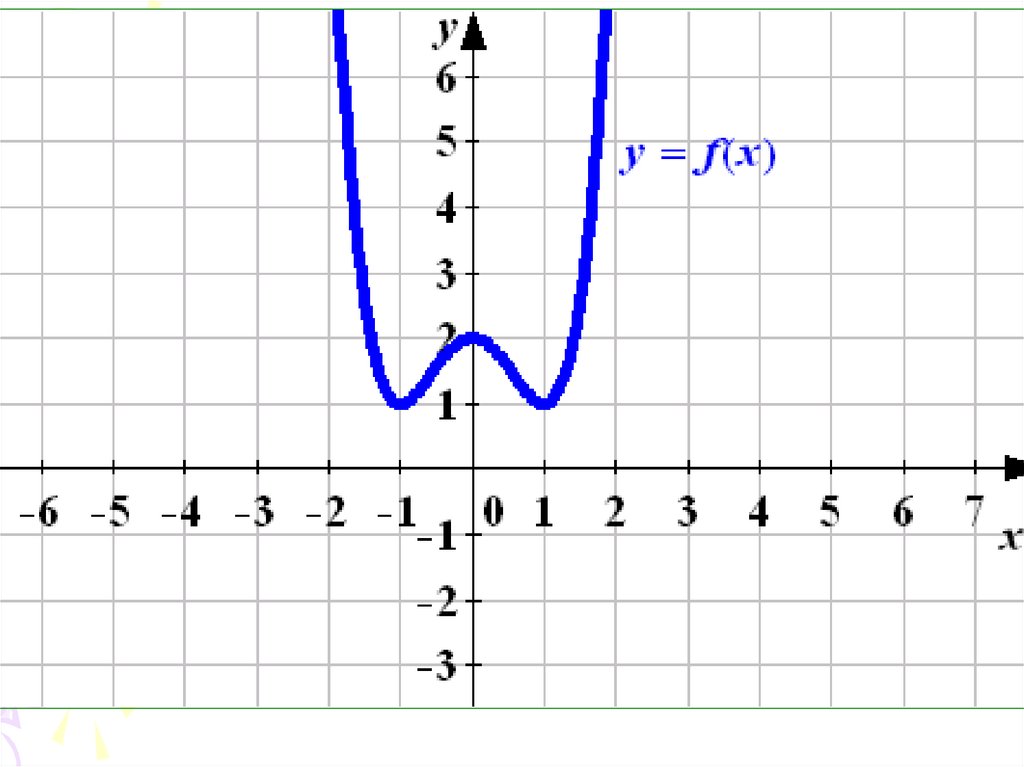
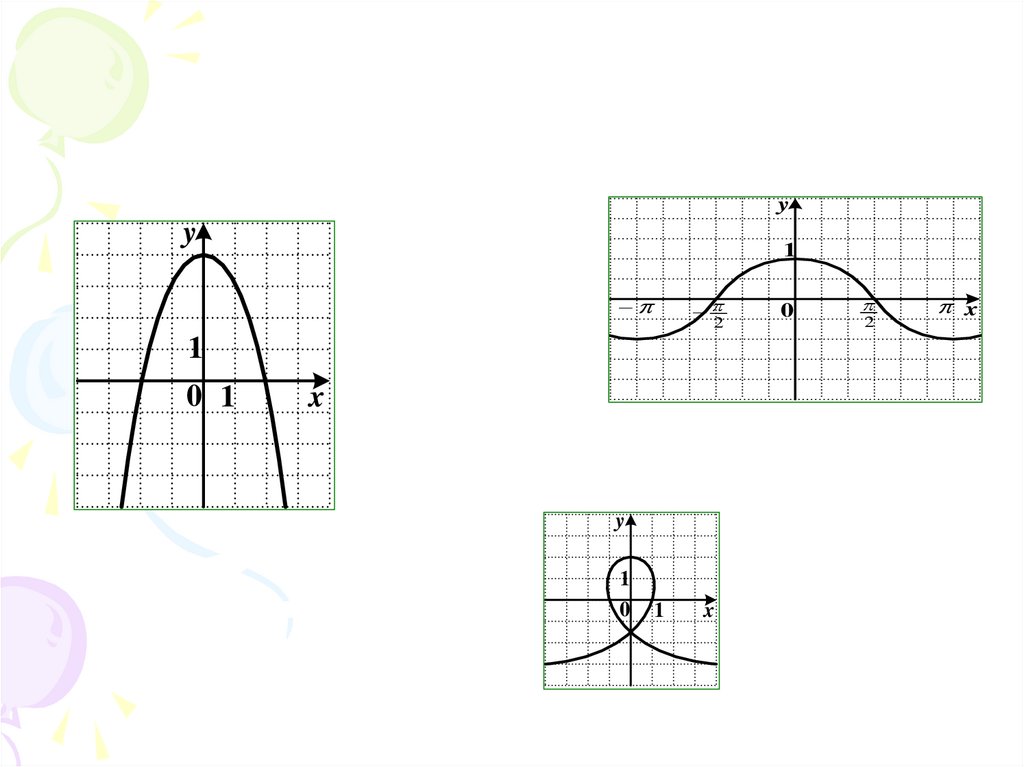
20. Функция y=f(x) называется четной, если выполняется равенство

f ( x) f ( x)

21.

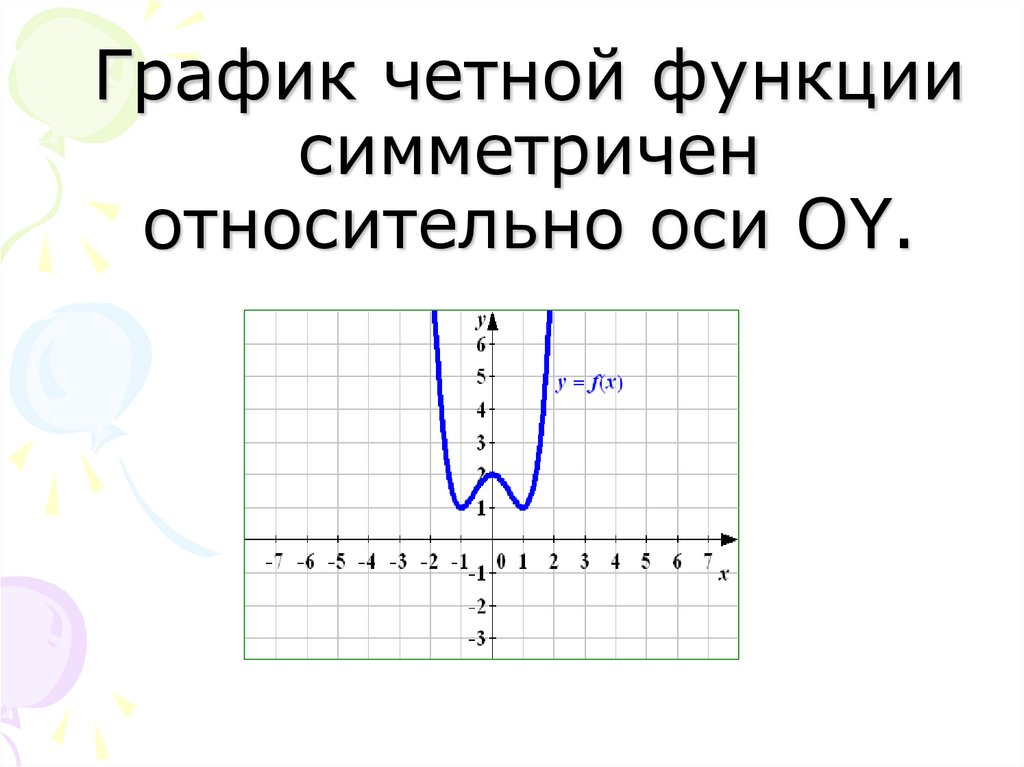
22. График четной функции симметричен относительно оси ОY.

23.

y
y
1
2
1
0 1
x
y
1
0
1
x
0
2
x

24. Функция y=f(x) называется нечетной, если выполняется равенство

f ( x) f ( x)

25.

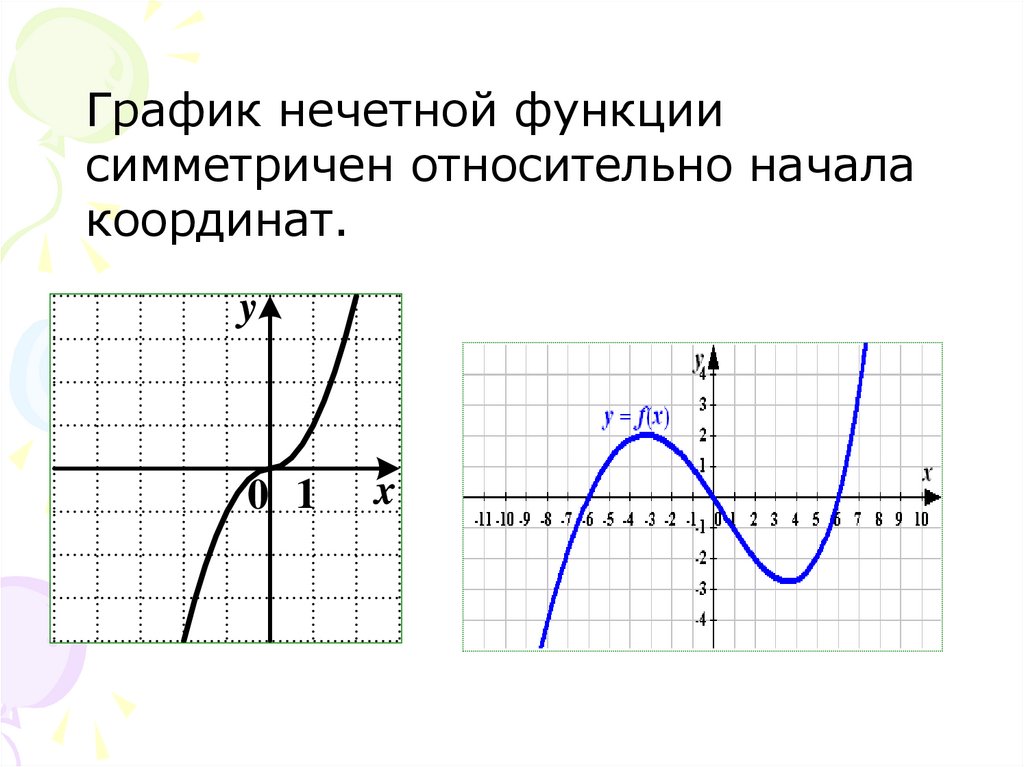
График нечетной функции
симметричен относительно начала
координат.
y
0 1
x

26.

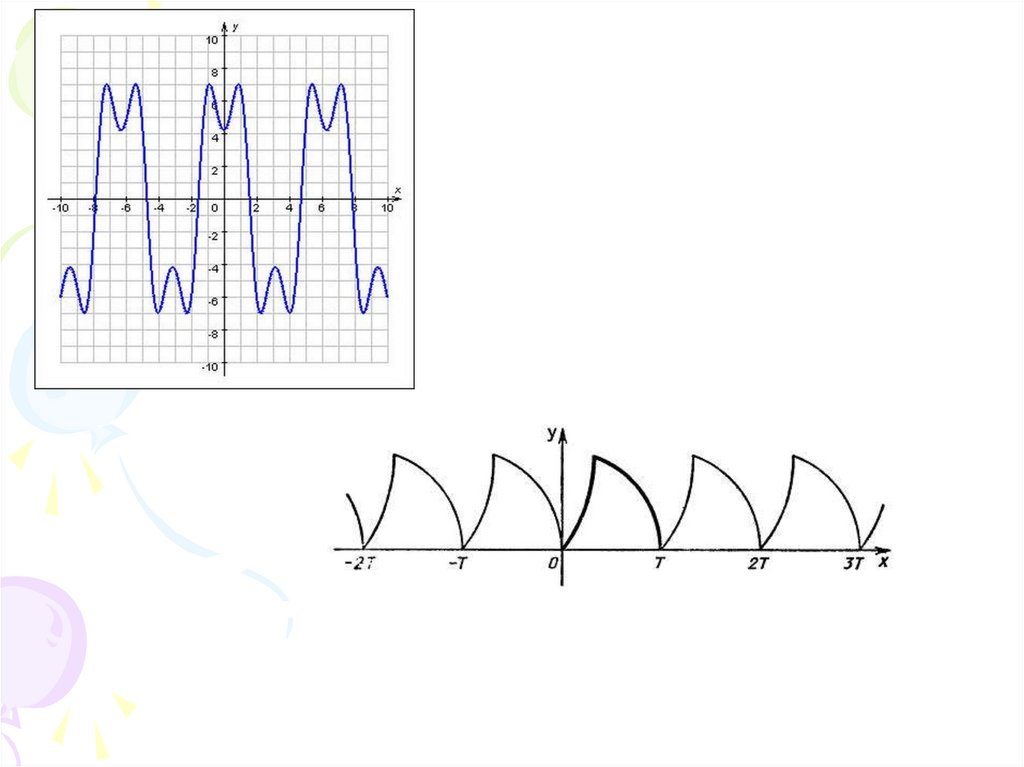
Периоди́ческая фу́нкция ― функция,
повторяющая свои значения через какой-то
регулярный интервал, то есть не меняющая своего
значения при добавлении к аргументу
фиксированного ненулевого числа (пери́ода
функции).
т.е.
Функция периодична, если существует такое число
T≠0 (период), что на всей области определения
функции выполняется равенство
f(x)=f(x+T) .

27.

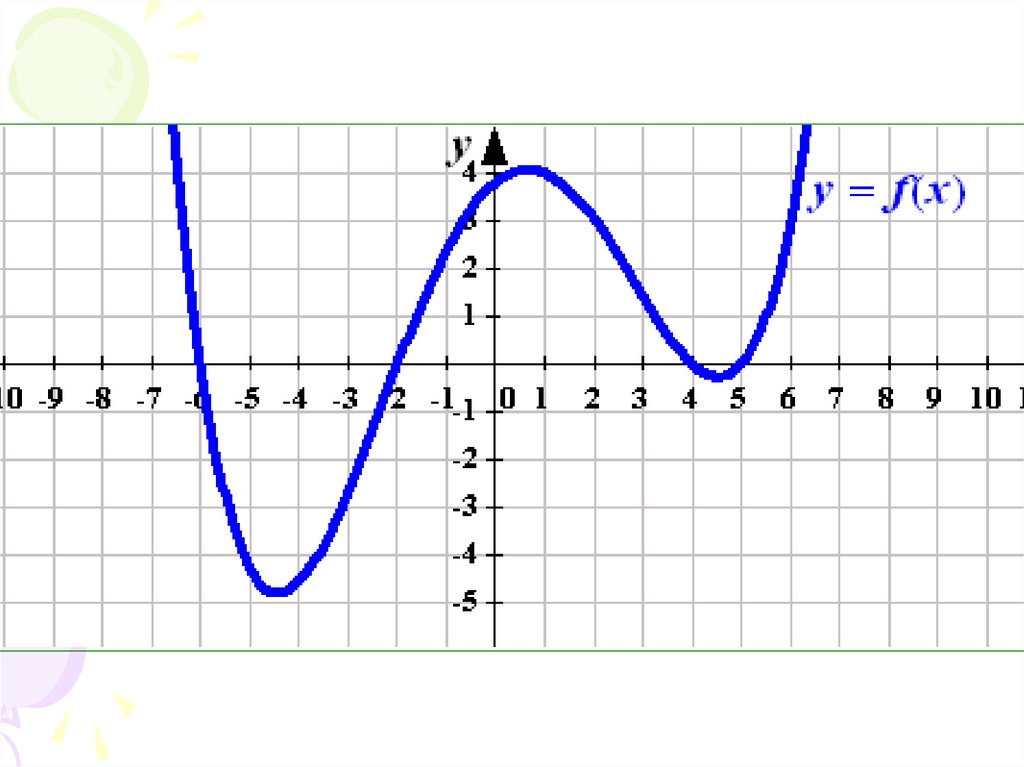
28. Экстремумы функции Определение 1. Точка   называется точкой максимума  функции y=f(x),  если существует такая   окрестность 

Определение 1. Точка
называется точкой
максимума функции y=f(x), если
существует такая окрестность точки x0,
что для всех значений
x≠ x0 из этой окрестности выполняется
неравенство f(x)‹f(x0) .
Определение 2. Точка
называется точкой
минимума функции y=f(x), если существует
такая окрестность точки x0, что для всех
значений
x≠ x0 из этой окрестности выполняется
неравенство f(x)›f(x0)

29. Определение 3. Значение функции в точке максимума называется максимумом  функции Определение 4. Значение функции в точке

Определение 3. Значение функции в точке максимума
называется максимумом функции
Определение 4. Значение функции в точке минимума
называется минимумом функции
Определение 5. Точки минимума и точки максимума
называются точками экстремума функции y=f(x) , а
значения функции в этих точках —
экстремумами функции y=f(x)

30. ОБРАТНАЯ ФУНКЦИЯ

Стр. 48 Алимов.
Если у= f(x) возрастает на (а;в)
то
х= g(у) убывает
на (а;в)

31. Схема исследования функции:

1. Найти область определения и область
значения функции.
2. Выяснить, является ли функция четной,
нечетной , периодической.
3. Вычислить нули функции
4. Найти промежутки знакопостоянства
функции.
5.Найти промежутки возрастания и убывания
функции.
6. Найти точки экстремума, экстремумы
функции.