Наклонная призма

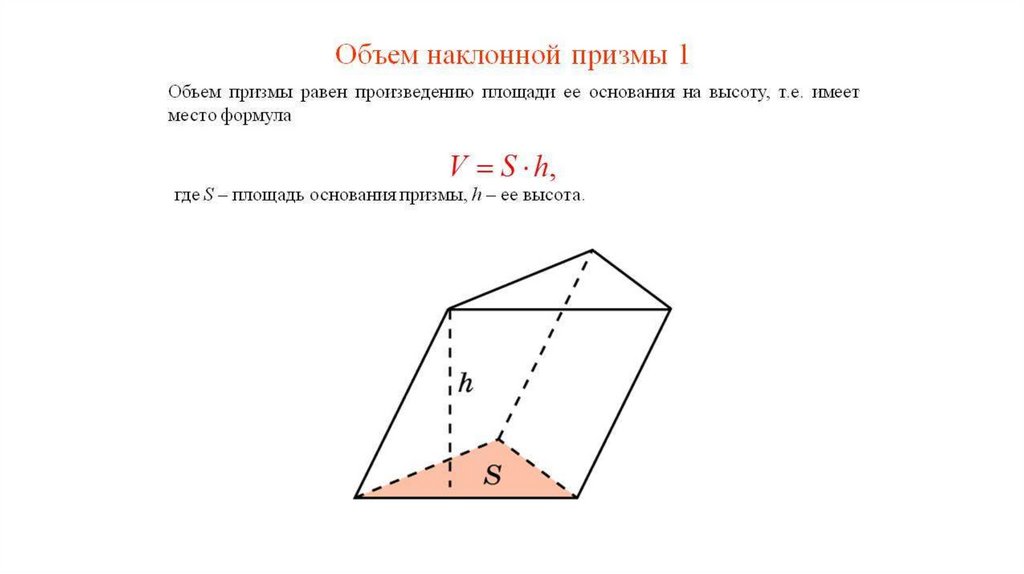
1.

2.

НАКЛОННАЯ ПРИЗМА

3.

Евклид определяет призму как телесную фигуру,
заключенную между двумя равными и
параллельными плоскостями (основаниями) и с
боковыми гранями - параллелограммами. Для того
чтобы это определение было вполне корректным,
следовало бы, однако, доказать, что плоскости,
проходящие через пары непараллельных сторон
оснований, пересекаются по параллельным
прямым.

4.

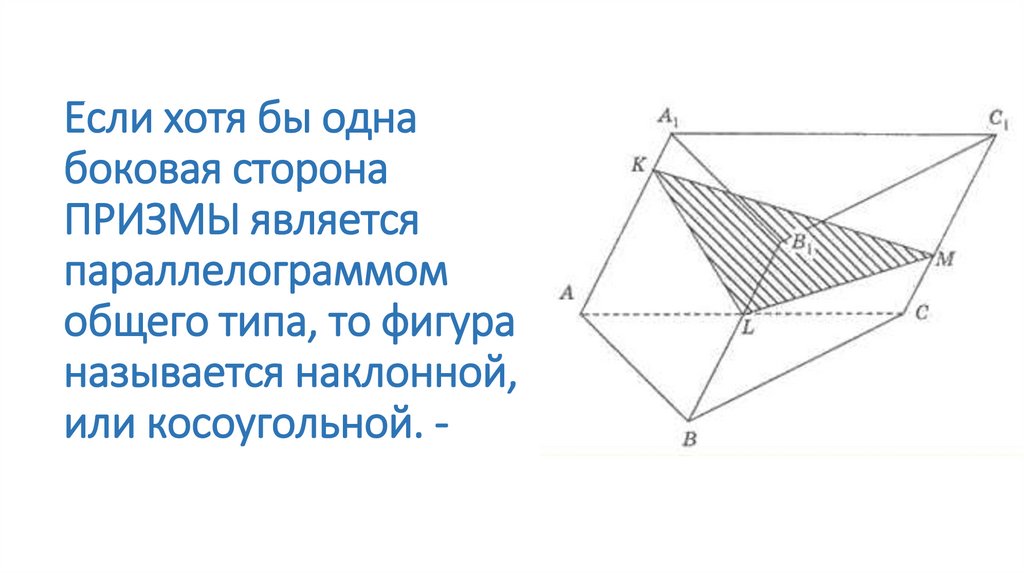
Если хотя бы одна
боковая сторона
ПРИЗМЫ является
параллелограммом
общего типа, то фигура
называется наклонной,
или косоугольной. -

5.

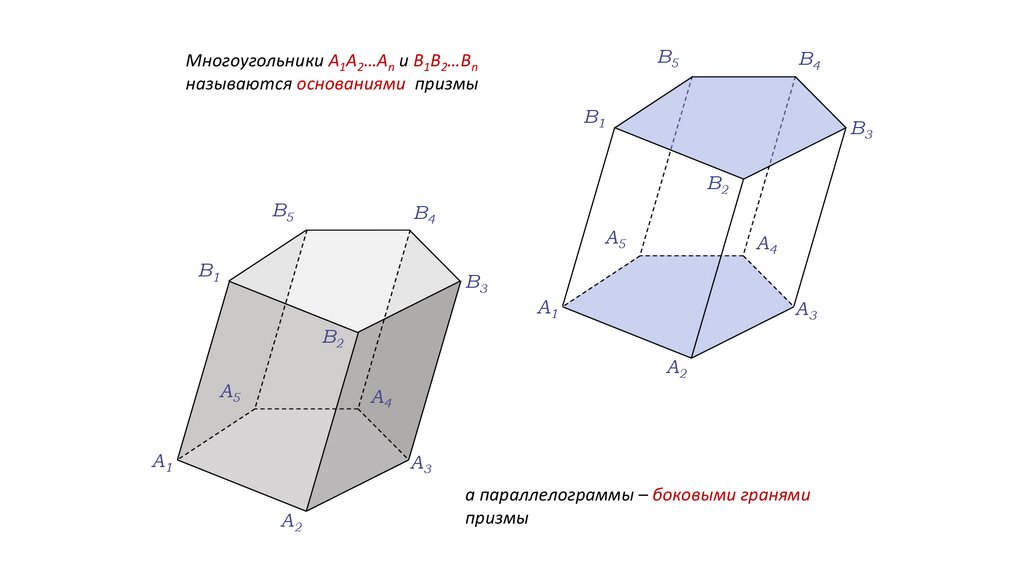
В5
Многоугольники A1A2…An и B1B2…Bn
называются основаниями призмы
В4
В1
В3
В2
В5
В4
В1
A5
В3
A4
A1
A3
В2
A2
A5
A4
A1
A3
A2
а параллелограммы – боковыми гранями
призмы

6.

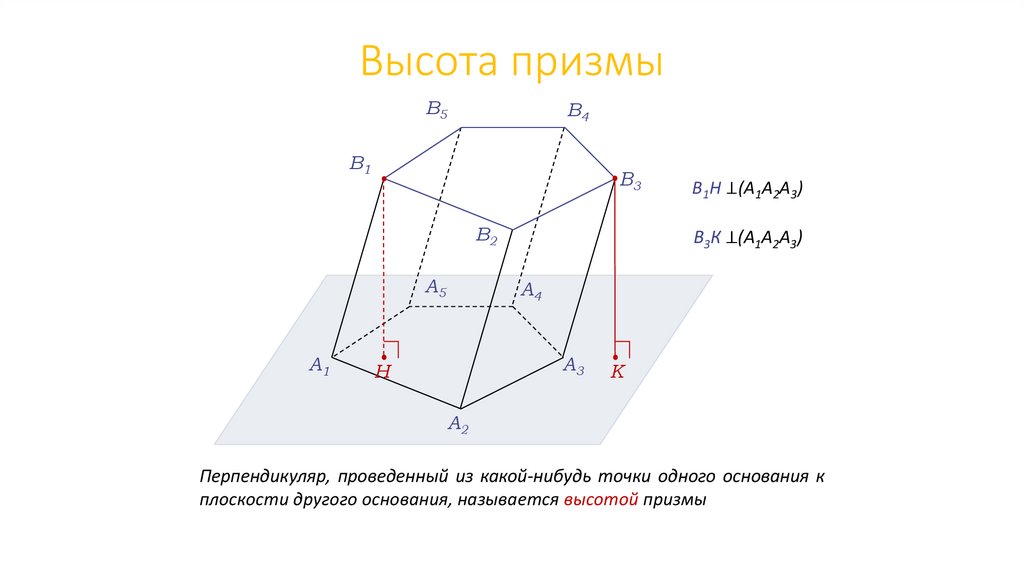
Высота призмы
В5
В4
В1
В3
В2
A5
A1
В1Н ⊥(А1А2А3)
В3К ⊥(А1А2А3)
A4
A3
Н
К
A2
Перпендикуляр, проведенный из какой-нибудь точки одного основания к
плоскости другого основания, называется высотой призмы

7.

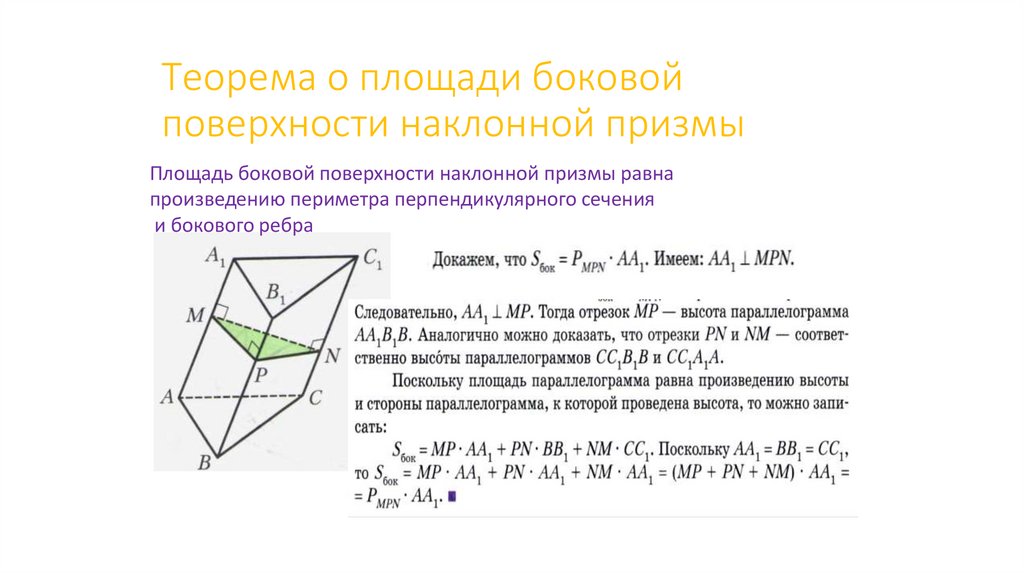
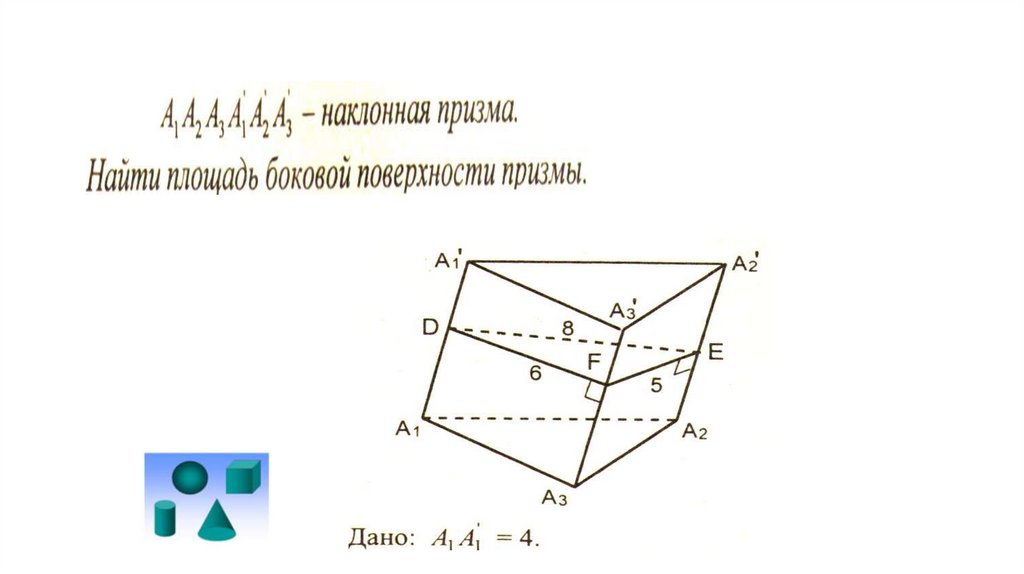
Теорема о площади боковой
поверхности наклонной призмы
Площадь боковой поверхности наклонной призмы равна
произведению периметра перпендикулярного сечения
и бокового ребра

8.

9.

10.

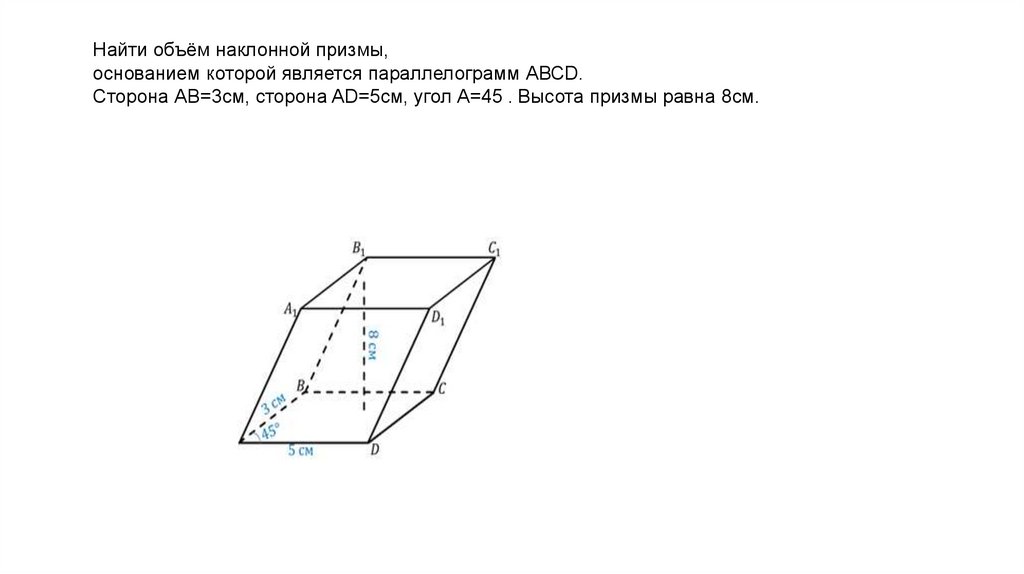
Найти объём наклонной призмы,
основанием которой является параллелограмм АВСD.
Сторона АВ=3см, сторона AD=5см, угол А=45 . Высота призмы равна 8см.

11.

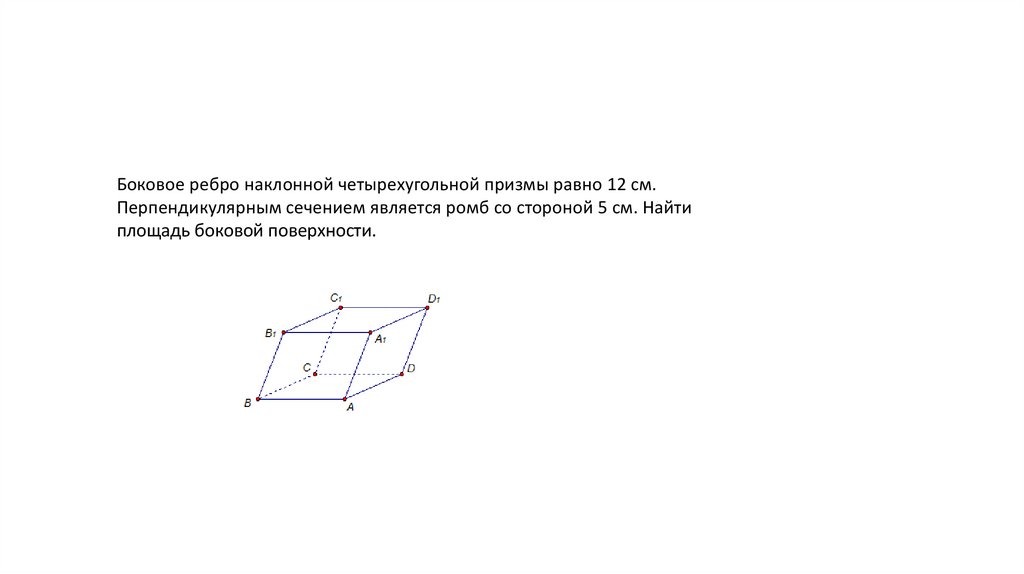
Боковое ребро наклонной четырехугольной призмы равно 12 см.
Перпендикулярным сечением является ромб со стороной 5 см. Найти
площадь боковой поверхности.

12.

Боковое ребро наклонной четырёхугольной призмы равно 8 см, а перпендикулярным сечением
является равнобедренная трапеция с основаниями 4 см и 2 см и углом при основании равным 45
градусам. Найти площадь боковой поверхности