Предел последовательности. Предел функции. Непрерывность функции

1.

Предел последовательности.
Предел функции.
Непрерывность функции.

2.

Если каждому числу n из натурального ряда чисел 1,2,3,…, n,…
поставлено в соответствие действительное число xn,
то множество действительных чисел x1, x2, x3,…, xn,…
называется числовой последовательностью (просто последовательностью).
Числа x1, x2, x3,…, xn,… -члены (элементы) последовательности,
xn - общий член последовательности,
n – номер члена (элемента).
(xn,) или xn
Способы задания последовательности:
•аналитический,
•табличный,
•графический а) на координатной плоскости, б) на координатной прямой.
•рекуррентный,
•словесный.

3.

Последовательность (xn,) называется ограниченной
сверху, если существует число М такое, что любой
член xn этой последовательности удовлетворяет
неравенство xn М.
Последовательность (xn,) называется ограниченной
снизу, если существует число m такое, что любой член
xn этой последовательности удовлетворяет
неравенству xn m.
Последовательность (xn,) называется ограниченной,
если она ограничена и сверху и снизу, т. е.
существуют числа m и М такие, что любой член xn, этой
последовательности удовлетворяет неравенствам m xn М.

4.

Последовательность (xn,) называется бесконечно большой,
если для любого положительного числа А существует номер N такой,
что при n N выполняется неравенство xn А.
Последовательность ( n) называется бесконечно малой,
если для любого положительного числа ε существует номер N такой,
что при n N выполняется неравенство n ε.
Теорема.
Если (xn,) – бесконечно большая последовательность, xn 0,
то последовательность ( n) =(1/ xn) - бесконечно малая, и, обратно,
если ( n)- бесконечно малая последовательность, ( n) 0,
то последовательность (xn) =(1/ n)- бесконечно большая.

5.

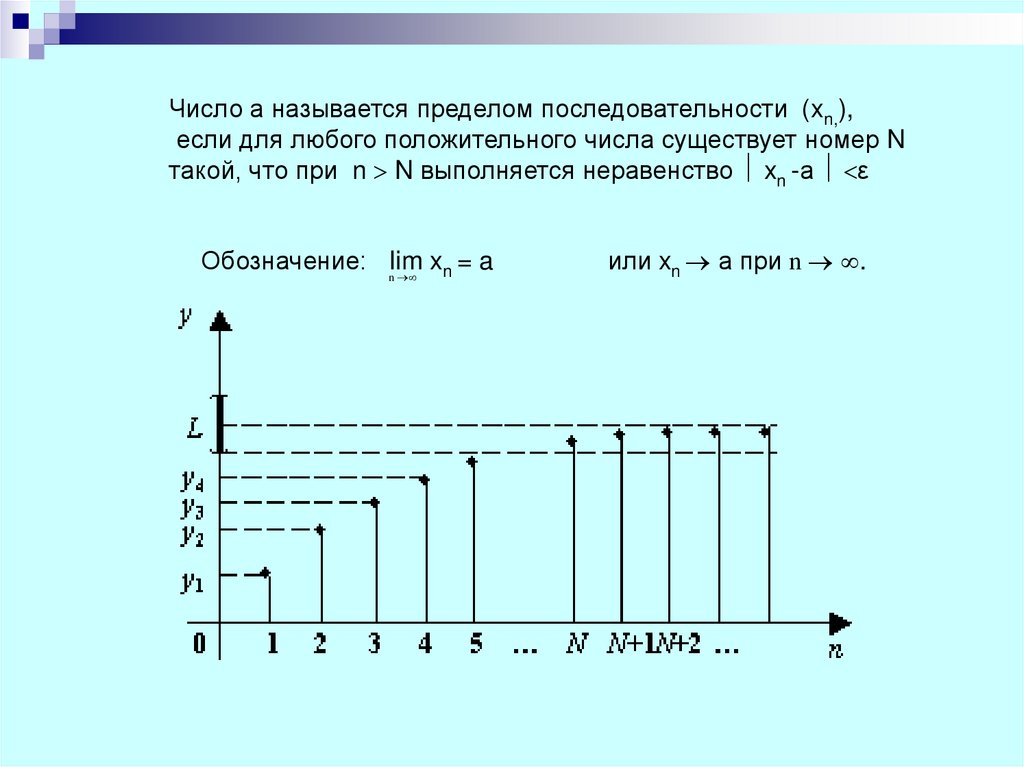
Число а называется пределом последовательности (xn,),
если для любого положительного числа существует номер N
такой, что при n N выполняется неравенство xn -а ε
Обозначение: Iim
xn = a
n
или xn а при n .

6.

7.

Основные свойства сходящихся последовательностей.
Т1. Сходящаяся последовательность ограничена.
Т2. Если lim xn = a, lim yn = b, тогда:
n
n
а) lim (x + y ) = a +b, b) lim (x y ) = a b, c) lim ( Xn /у ) =a/b (b 0).
n
n
n
n n
n n
n
Т3. Если lim xn = а, lim zn =а и для всех n выполняются неравенства
n
n
xn yn zn , то lim yn = 0
n
( произведение бесконечно малой на ограниченную есть бесконечно малая).