Решение задач на окружность

1.

Тридцатое марта
Классная работа
Решение задач на окружность

2.

Геометрическим местом точек
(ГМТ)
называют множество всех точек,
обладающих определённым
свойством.

3.

А
СЕРЕДИННЫЙ ПЕРПЕНДИКУЛЯР
отрезка является геометрическим
местом точек, равноудалённых
от концов этого отрезка

4.

А
БИССЕКТРИСА угла является
геометрическим местом точек,
принадлежащих углу и равноудалённых
от его сторон

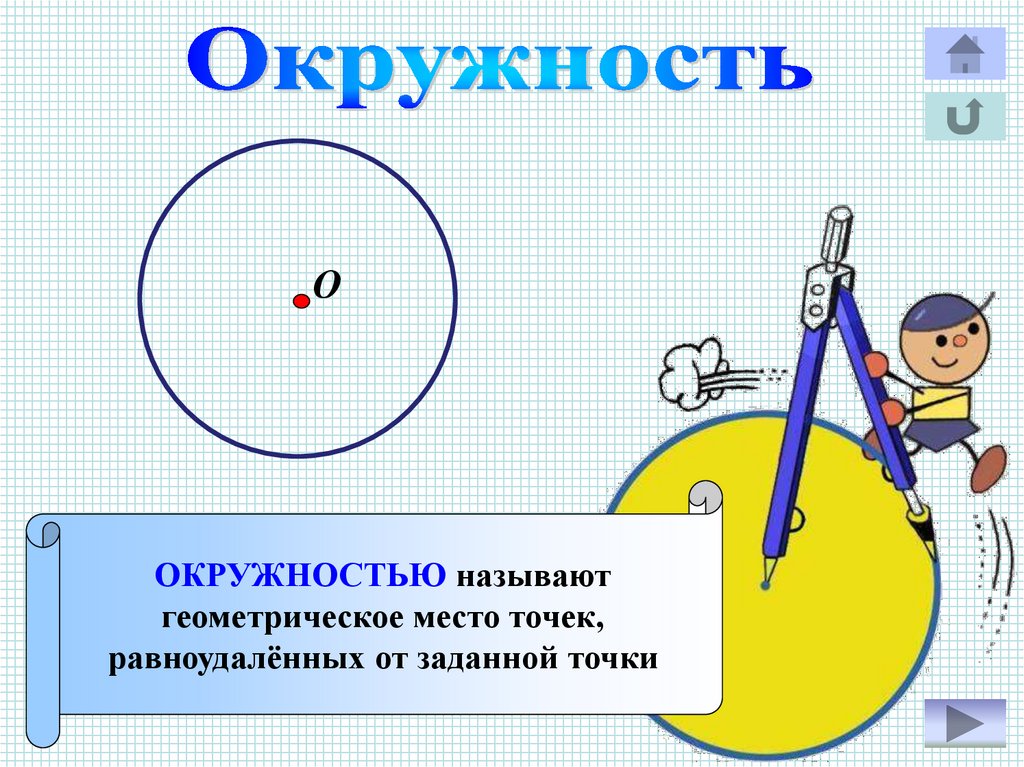
5.

О
ОКРУЖНОСТЬЮ называют
геометрическое место точек,
равноудалённых от заданной точки

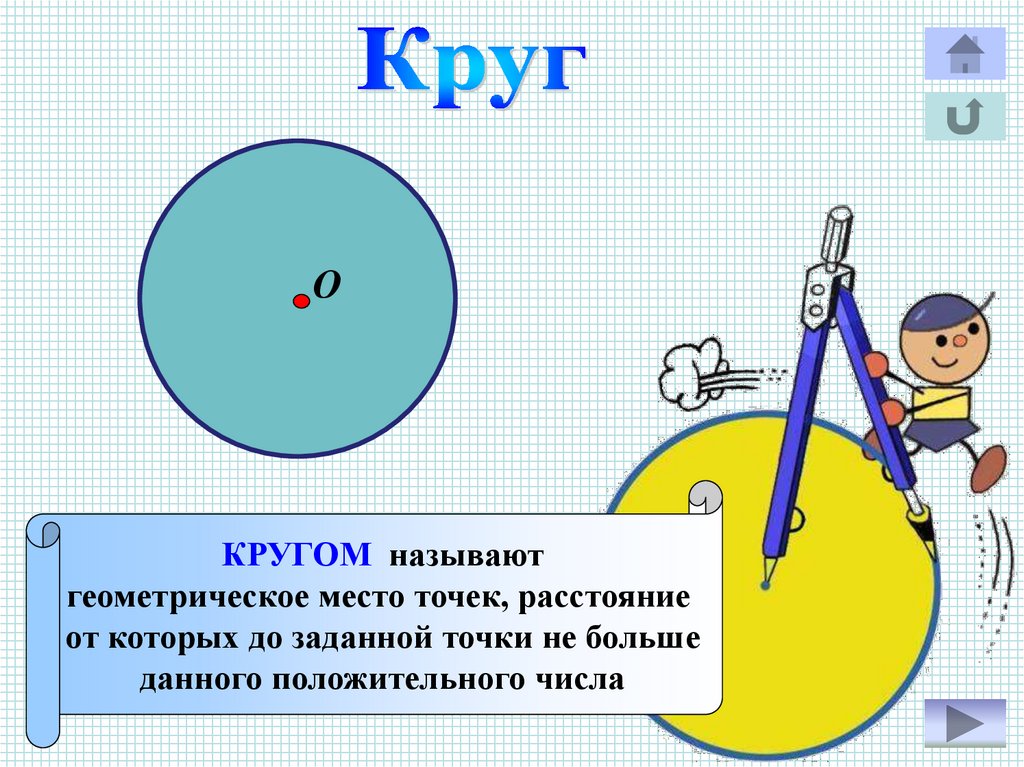
6.

О
КРУГОМ называют
геометрическое место точек, расстояние
от которых до заданной точки не больше
данного положительного числа

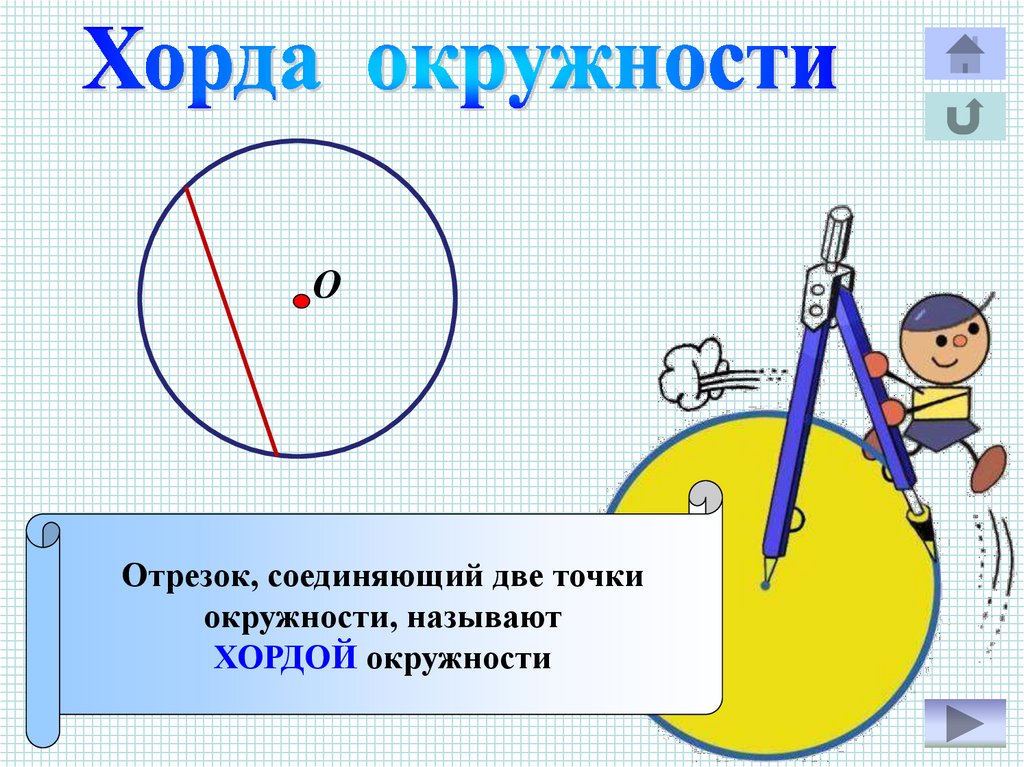
7.

О
Отрезок, соединяющий две точки
окружности, называют
ХОРДОЙ окружности

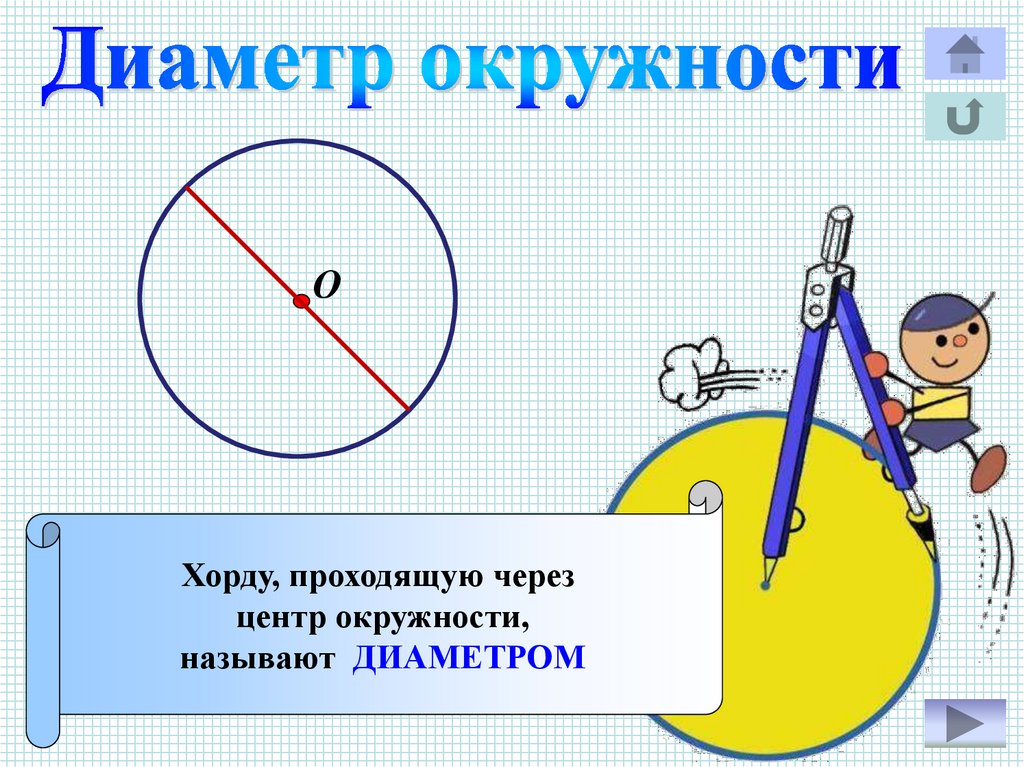
8.

О
Хорду, проходящую через
центр окружности,
называют ДИАМЕТРОМ

9.

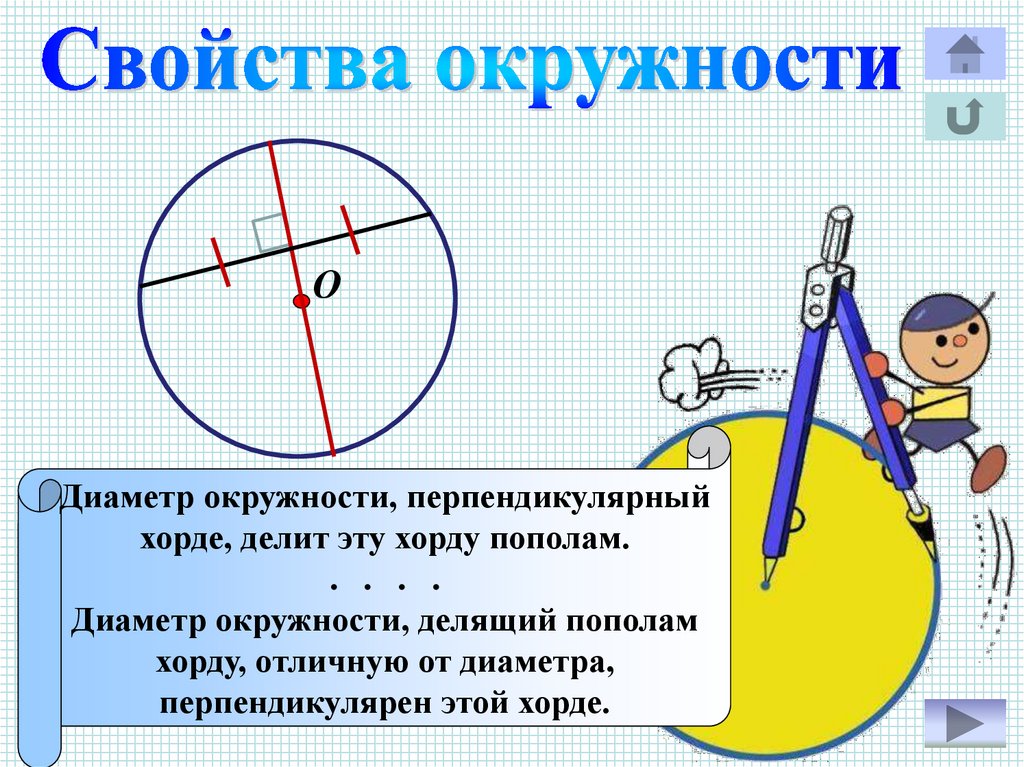
О
Диаметр окружности, перпендикулярный
хорде, делит эту хорду пополам.
. . . .
Диаметр окружности, делящий пополам
хорду, отличную от диаметра,
перпендикулярен этой хорде.

10.

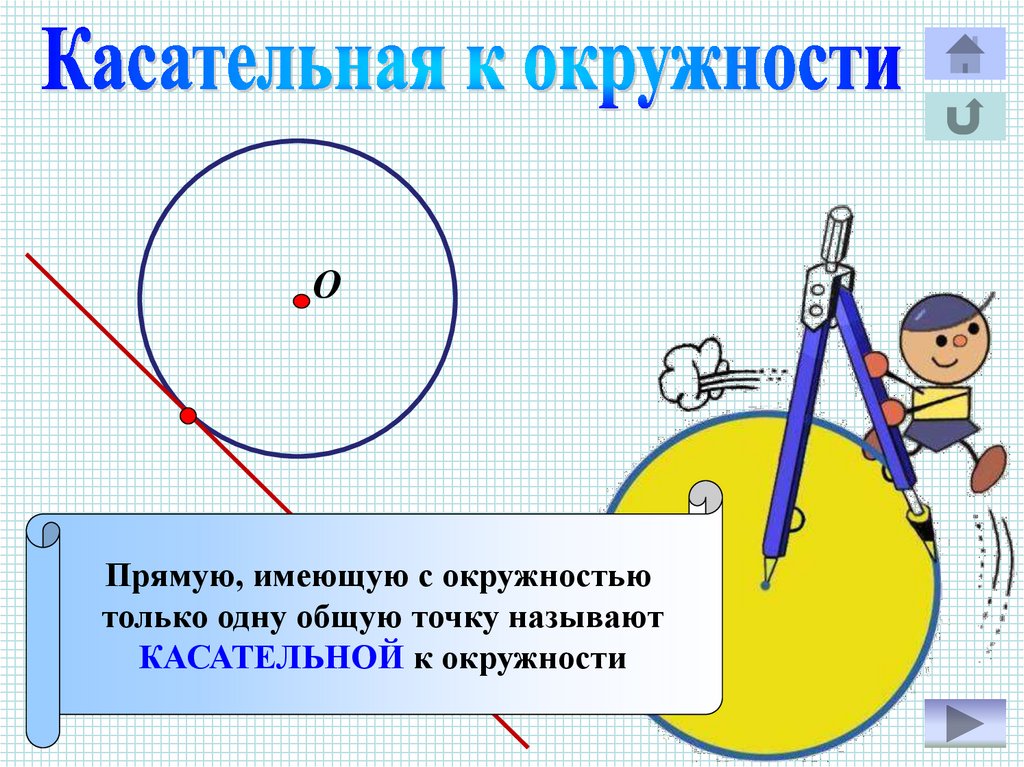
О
Прямую, имеющую с окружностью
только одну общую точку называют
КАСАТЕЛЬНОЙ к окружности

11.

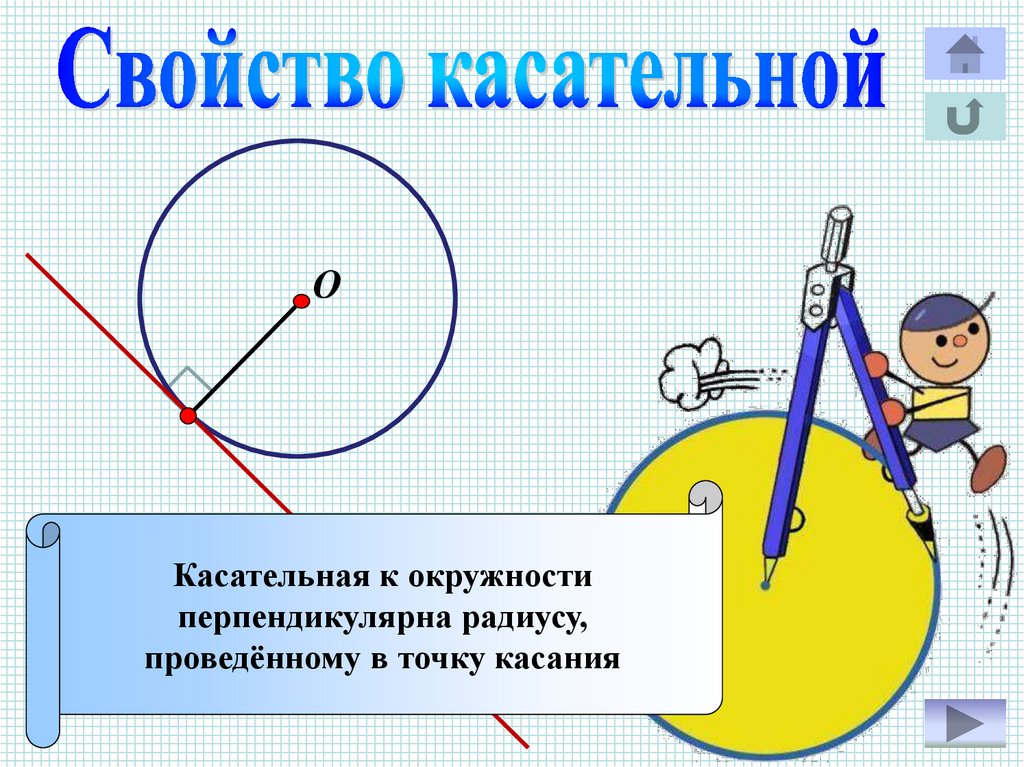
О
Касательная к окружности
перпендикулярна радиусу,
проведённому в точку касания

12.

О
Если прямая, проходящая через точку
окружности, перпендикулярна радиусу,
проведённому в эту точку то эта прямая
является касательной к данной окр-ти

13.

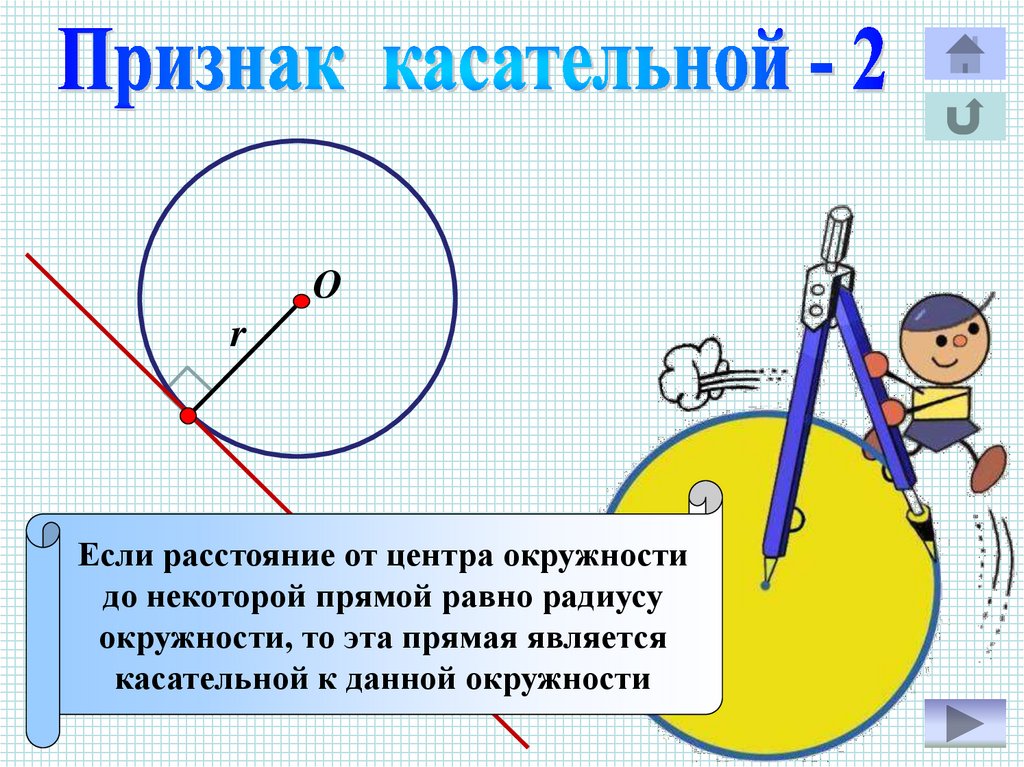
О
r
Если расстояние от центра окружности
до некоторой прямой равно радиусу
окружности, то эта прямая является
касательной к данной окружности

14.

О
r
Если расстояние от центра окружности
до некоторой прямой равно радиусу
окружности, то эта прямая является
касательной к данной окружности

15.

О
А
Отрезки касательных
к окружности,
проведённых из одной точки, равны
п составляют равные углы с прямой,
проходящей через эту точку и центр окр-ти

16.

О
Окружность называют описанной около
треугольника, если она проходит через
все вершины этого треугольника

17.

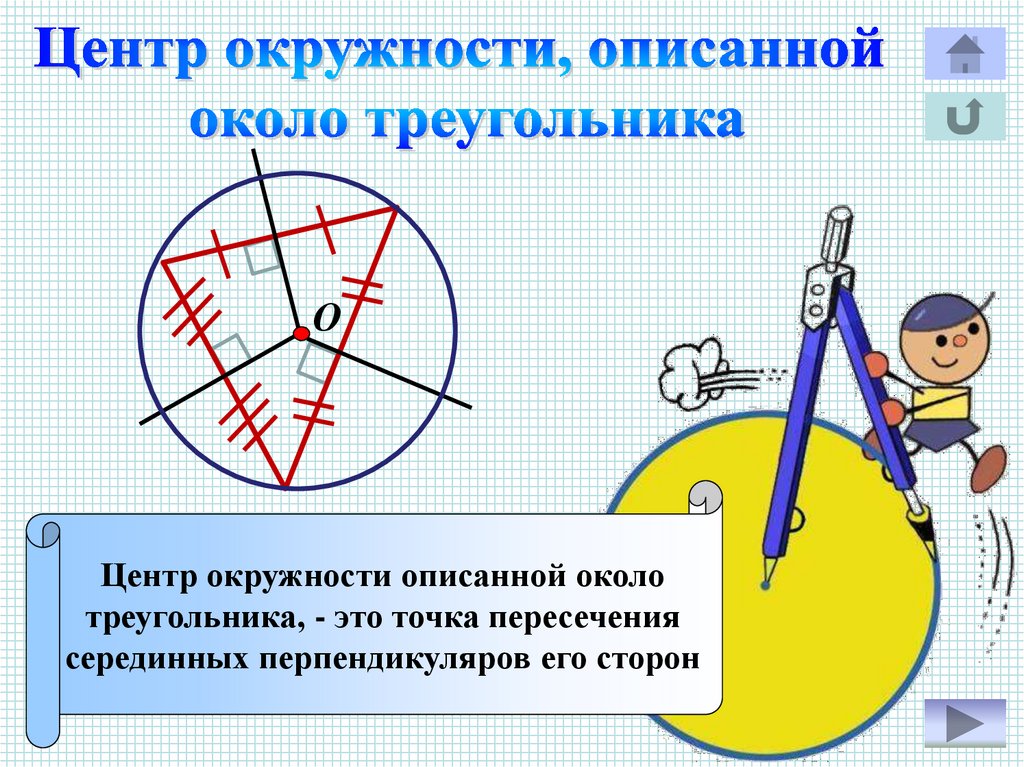
О
Центр окружности описанной около
треугольника, - это точка пересечения
серединных перпендикуляров его сторон

18.

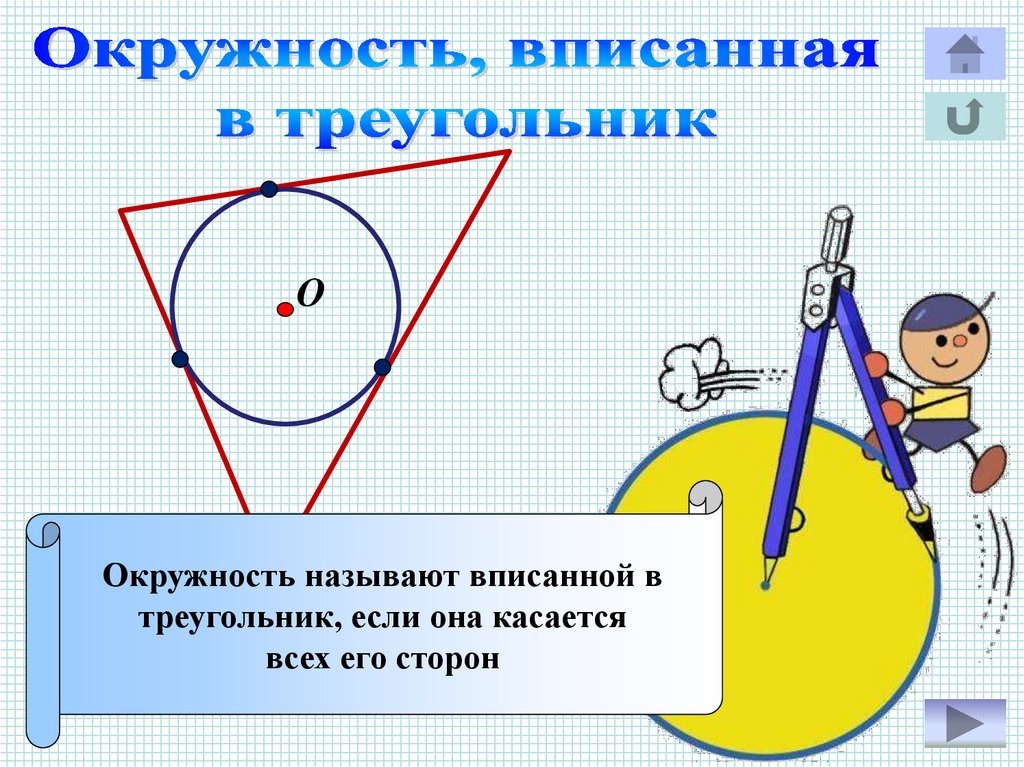
О
Окружность называют вписанной в
треугольник, если она касается
всех его сторон

19.

О
Центр окружности, вписанной в
треугольник, - это точка пересечения
его биссектрис

20.

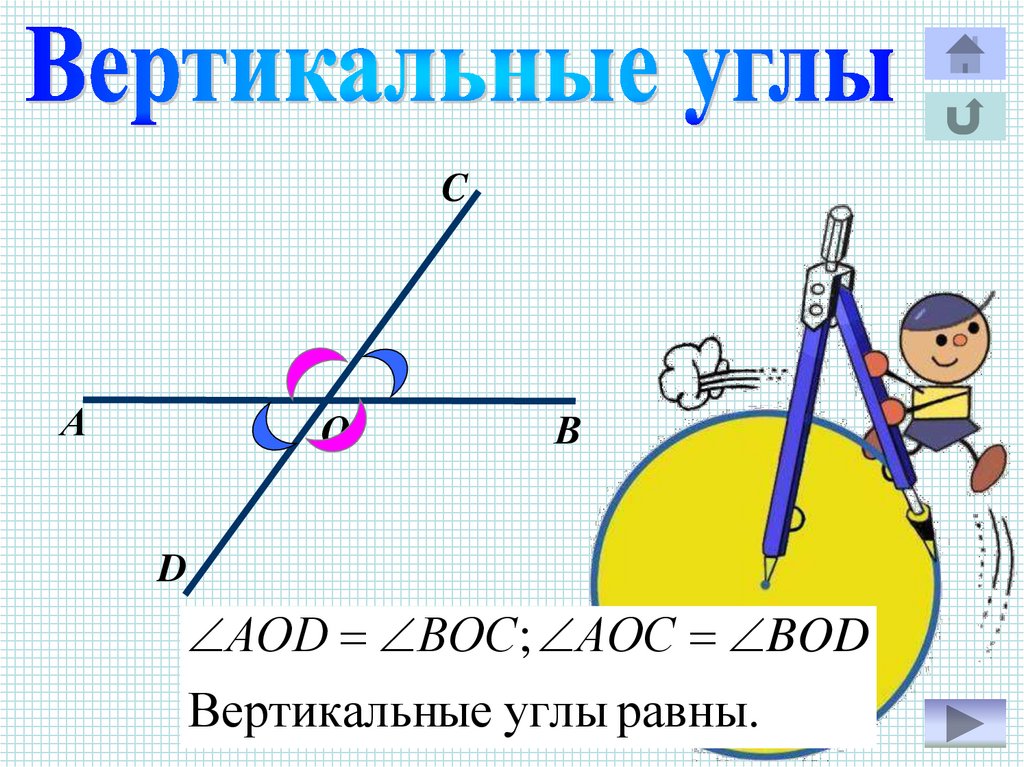
C
А
О
В
D
АОD ВОC; АОС BOD
Вертикальные углы равны.

21.

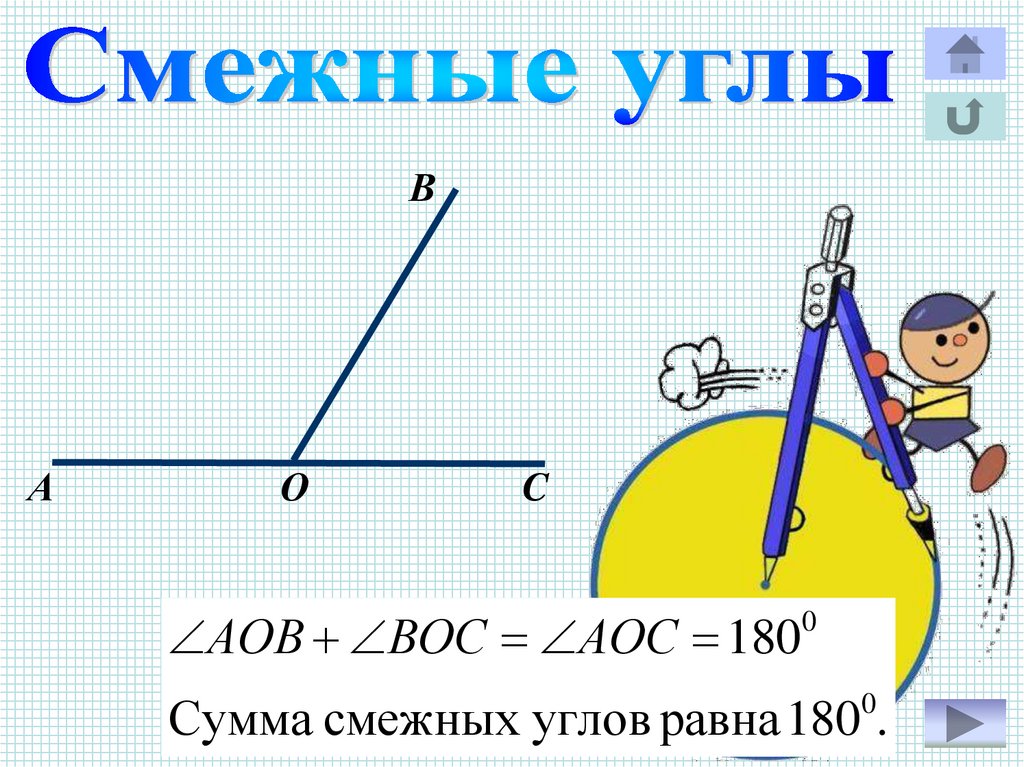
В
А
О
C
АОB ВОC АОС 180
0
Сумма смежных углов равна 180 .
0

22.

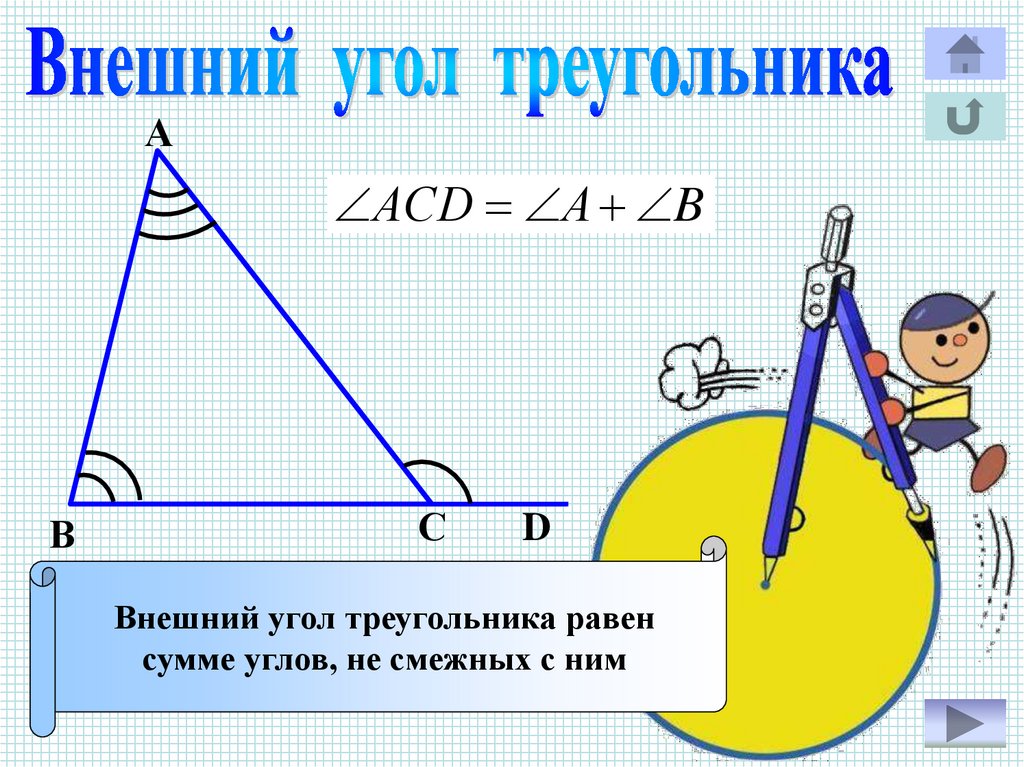
А
АСD А B
В
С
D
Внешний угол треугольника равен
сумме углов, не смежных с ним

23.

А
С
1
АC АВ
2
30º
В
Против угла в 30º лежит катет
равный половине гипотенузы

24.

А
По катетам
КАТЕТ
По катету и гипотенузе
С
По катету и прилеж.
острому углу
По гипотенузе
и острому углу
КАТЕТ
В

25.

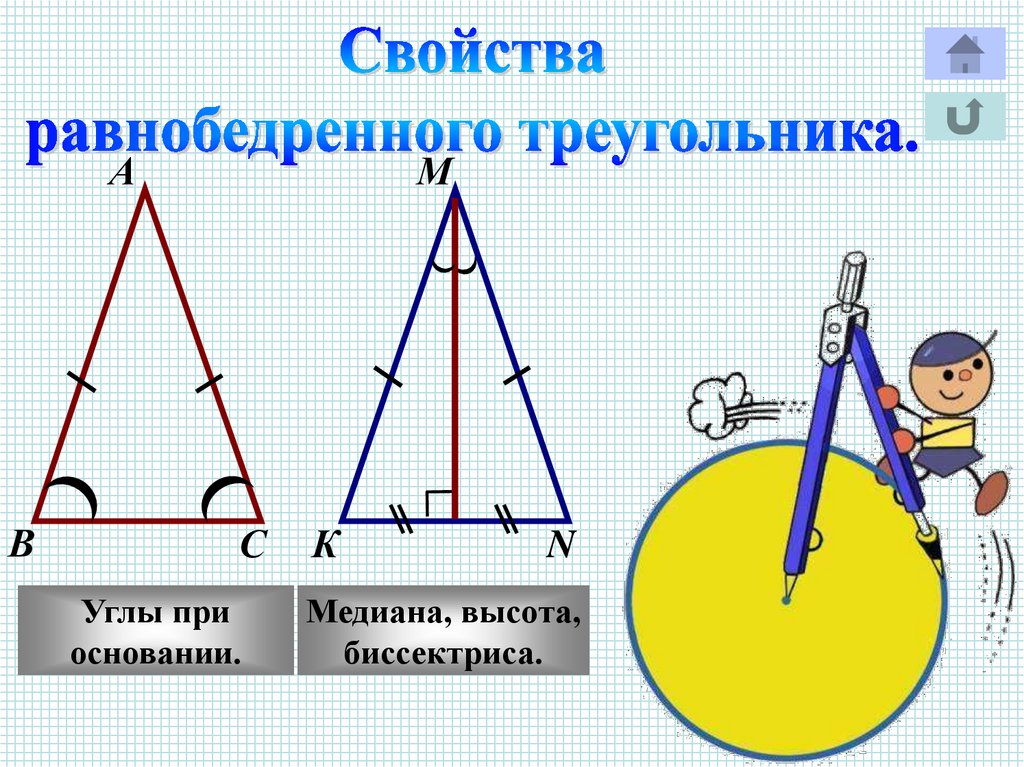
А
В
М
С
Углы при
основании.
К
N
Медиана, высота,
биссектриса.

26.

27.

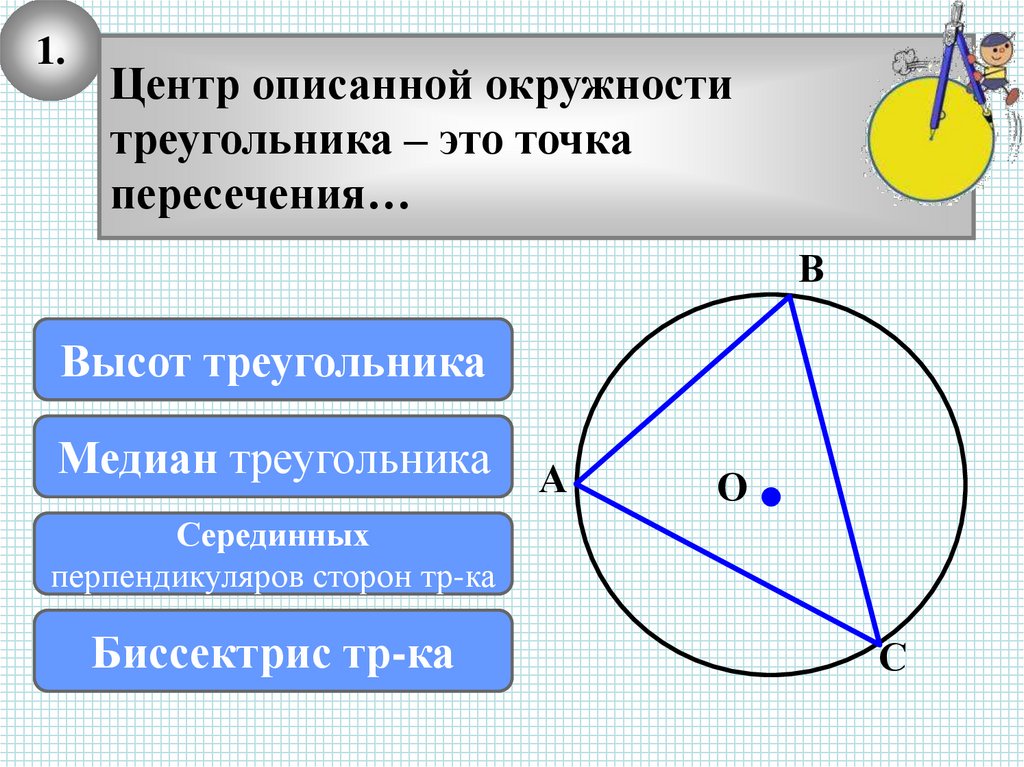
1.
Центр описанной окружности
треугольника – это точка
пересечения…
В
Высот
треугольника
Подумай!
Медиан
треугольника
Подумай!
А
O
Серединных
МОЛОДЕЦ
перпендикуляров
сторон тр-ка
Биссектрис
тр-ка
Подумай!
С

28.

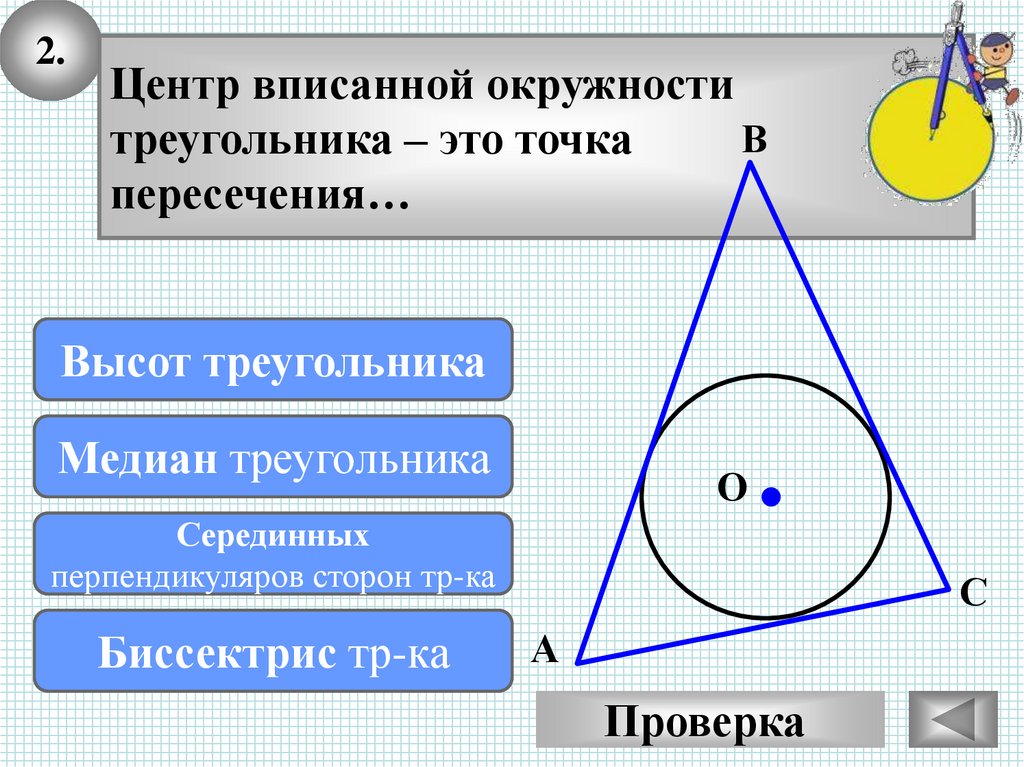
2.
Центр вписанной окружности
В
треугольника – это точка
пересечения…
Высот
треугольника
Подумай!
Медиан
треугольника
Подумай!
O
Серединных
Подумай!
перпендикуляров
сторон тр-ка
Биссектрис
тр-ка
МОЛОДЕЦ
С
А
Проверка

29.

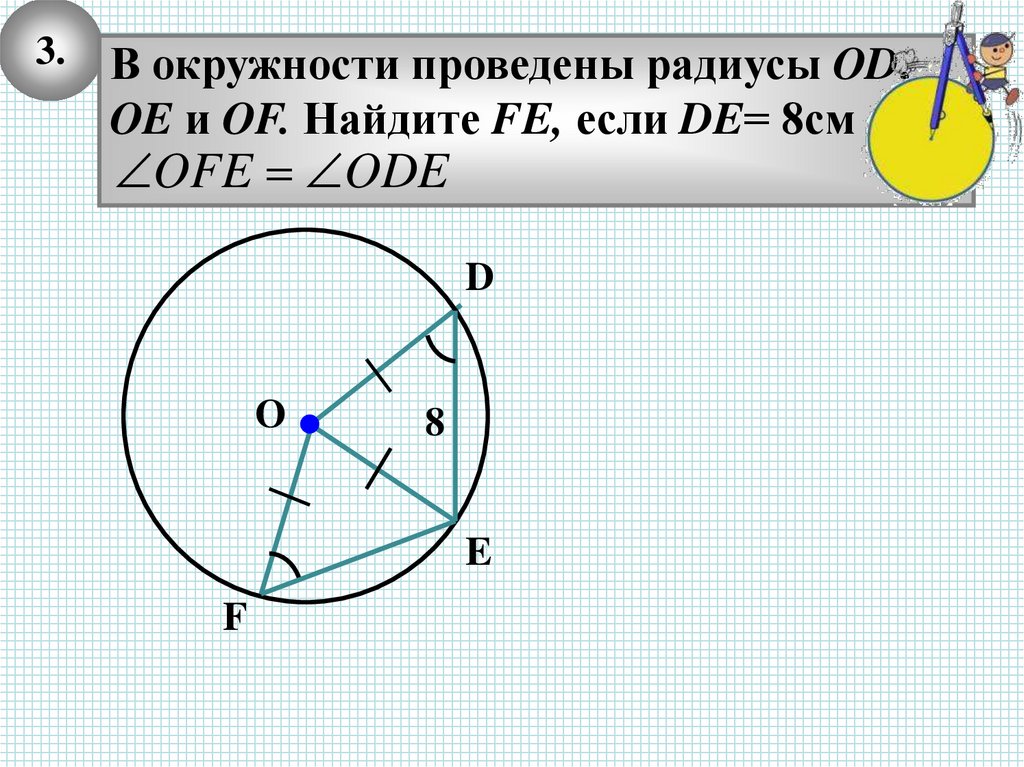
3.
В окружности проведены радиусы OD,
OE и OF. Найдите FE, если DE= 8см
OFE ODE
D
O
8
E
F

30.

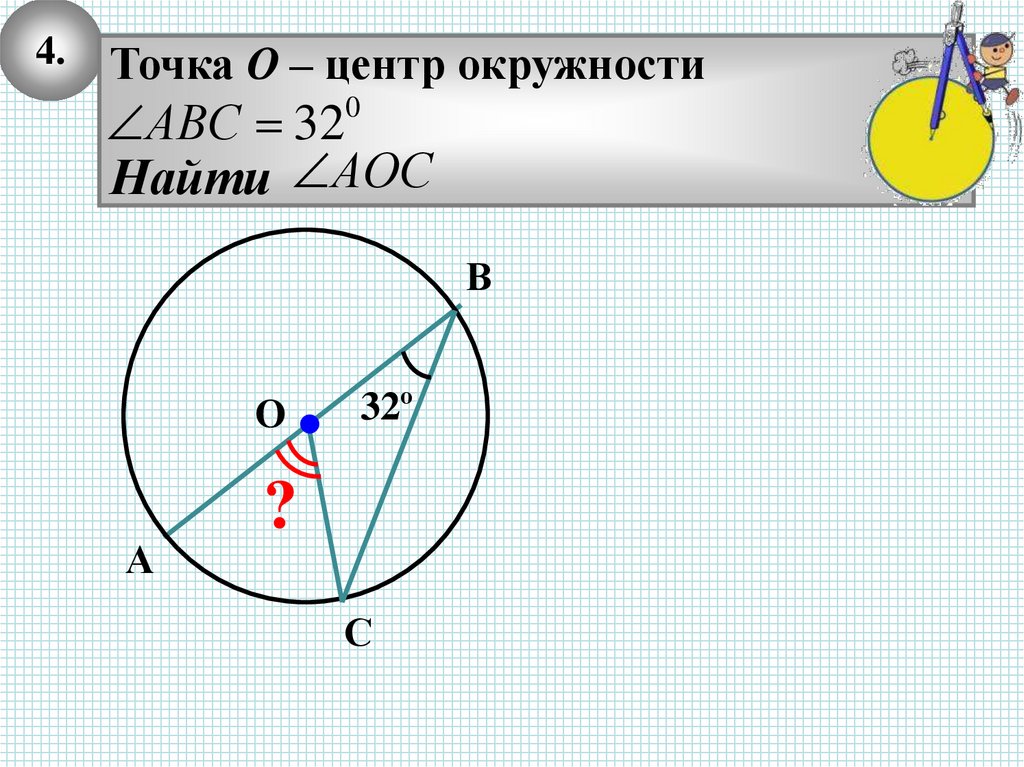
4.
Точка О – центр окружности
АВС 32
Найти АОС
0
В
O
А
32º
?
С

31.

5.
В окружности хорда CD пересекает
0
диаметр АВ в точке К, DKА 60
0
DEK CFK 90 , EF = 10 см
Найдите хорду CD
D
А
O F
60º
E
K
С
В

32.

Домашнее задание:
Выучить: п.70-78
Выполнить: №653(а, в), №655