Решение задач по геометрии. Нахождение угла между прямой и плоскостью

1.

Решение задач
по геометрии
Нахождение угла
между прямой и
плоскостью

2.

Прямая и плоскость пересекаются, если они имеют одну
единственную общую точку, которую называют точкой
пересечения прямой и плоскости.
Прямая перпендикулярна к плоскости, если она
перпендикулярна к любой прямой, лежащей в этой
плоскости.

3.

Проекцией точки М на плоскость α называется либо сама точка М,
если М лежит в плоскости α , либо точка пересечения плоскости α и прямой,
перпендикулярной к плоскости α и проходящей через точку М, если точка М
не лежит в плоскости α .
α
α

4.

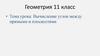
Проекцией прямой a на плоскость α называют
множество проекций всех точек прямой a на плоскость
.
α
α

5.

6.

Определение.
Нормальным вектором плоскости (или нормалью плоскости) называют вектор,
перпендикулярный данной плоскости.
Плоскости, пересекаясь, образуют четыре двугранных
угла: два тупых и два острых или четыре прямых,
причем оба тупых угла равны между собой, и оба
острых тоже равны между собой. Мы всегда будем
искать острый угол. Для определения его величины
возьмем точку на линии пересечения плоскостей и в
этой точке в каждой из плоскостей проведем
перпендикуляры к линии пересечения. Нарисуем
также нормальные векторы к каждой плоскости.
Отложим их от точки О.

7.

Вычислять угол между векторами мы умеем по формуле
Но! Мы при решении задач можем выбрать нормали
так, что угол между векторами будет тупой. А угол
между плоскостями не может быть тупой.

8.

Итак, если угол между нормалями острый, то мы сразу получаем угол между плоскостями
(формула со знаком «+»).
Если угол между нормалями тупой, то чтобы получить косинус острого угла, надо взять
полученное числовое значение для косинуса со знаком «–».
А лучше и проще применить знак модуля.

9.

10.

Основание прямой четырехугольной призмы ABCDA1B1C1D1 прямоугольник
ABCD, в котором AB = 5, AD =
. Найдите тангенс угла33между плоскостью
грани AA1D1D и плоскостью, проходящей через середину ребра CD
перпендикулярно прямой B1D, если расстояние
3
между прямыми A1C1 и BD равно .
D1
C1 Расстояние между прямыми
A1C1 и BD?
Решим задачу методом координат.
B1
Введем нормали к плоскостям.
A
z
1
1. Нормаль к плоскости АDD1
DC
3
D
C
33
x A
5
B
y
2. Нормаль ко второй плоскости ,
которую я и строить не берусь… Но по
условию это сечение проходит
перпендикулярно прямой В1D. Значит,
В1D перпендикуляр к плоскости.
Выберем нормаль B1D.
DB1

11.

Основание прямой четырехугольной призмы ABCDA1B1C1D1 прямоугольник
33 между плоскостью
ABCD, в котором AB = 5, AD =
. Найдите тангенс угла
грани AA1D1D и плоскостью, проходящей через середину ребра CD
перпендикулярно прямой B1D, если расстояние
3
между прямыми A1C1 и BD равно .
z
A1
D1
C1
B1 ( 33; 5; )3
3
Я выбрала очень удобно нормальные
векторы. Ведь это радиус-векторы.
Координаты радиус-вектора такие же,
как и координаты конца вектора.
Значит, нам надо найти координаты
точек В1 и С.
3
1. DB1
D
C (0; 5; 0)
y
33
x A
5
B
2. DC

12.

DC (0; 5; 0)
DB1 ( 33; 5; )3
3. cos
Теперь найдем тангенс.
2
tg A 1
x1 x2 y1 y2 z1 z2
x12 y12 z12 x22 y22 z22
tg 1
1
2
cos
33 0 5 5 3 0
33 5 3 0 5 0
2
2
2
2
2
5
61
2
61
tg 1
25
2
0 25 0
25
5
.
61
5
61
33 25 3 25
cos
2
1
cos2 A
5
61
tg 2
61
1
25
36
tg
25
2
tg
6
5
6
tg
5
т.к. – острый угол