Нерівності, що містять змінну під знаком модуля

1. Розв'яжіть нерівність ( усно)

2х < 8,
0х < -7,
3х 6,
0х < 8,
0х > 11,
-3х > 12,
-6х < -18,
- х < 1,
- х > 0,
-5х < 1,
-5 < 2х <6,
-7 3х 9
14 2х < 11
-16 < 4х -24
-1 < 7х< 2

2. Яка нерівність відповідає кожному з проміжків?

3
х
6
х
-7
-5
3
х
8
х
9
х
-3
2
х

3.

Знайдіть помилку
Чи правильно записана множина розв'язків системи?
0
х
5
-5
( 5; )
0
х
2
(-5;2)
7
розв'язків немає
х
6
(- ; 8 )
8
х

4. Розв'яжіть систему

х 1;
х 2,
х 4;
х 7,
х 1;
х 4,

5.

ТЕМА УРОКУ:
“Нерівності, що містять
змінну під знаком модуля”

6. Що таке модуль?

1)
2)
3)
4)
5)
Чому дорівнює модуль нуля?
Чому дорівнює модуль додатного числа?
Чому дорівнює модуль від'ємного числа?
Чому дорівнює модуль числа, яке позначене на
координатній прямій?
Що означає |3|= 3? |-3|= 3?
-3
0
х

7. Нерівність |х|<а,(а>0).

Нерівність |х|<а,(а>0).
Приклад1.|х|=6. Що означає ця рівність?
Приклад 2. |х|<6. Що означає ця нерівність?
Де розміщені на координатній прямій точки, координати яких
мають таку властивість?
-6
6
x
Яка нерівність відповідає цьому проміжку?
Отже, нерівність |х|<6 рівносильна подвійній нерівності :
- 6 < x <6.
Відповідь: (-6;6)

8. Нерівність |х|>а,(а>0)

Нерівність |х|>а,(а>0)
|х|> 5. Що означає ця нерівність?
Де розміщені на координатній прямій точки, що мають таку
властивість?
-5
0
5
х
Які нерівності відповідають цим числовим проміжкам?
х< -5
і х > 5, або
х 5;
х 5.

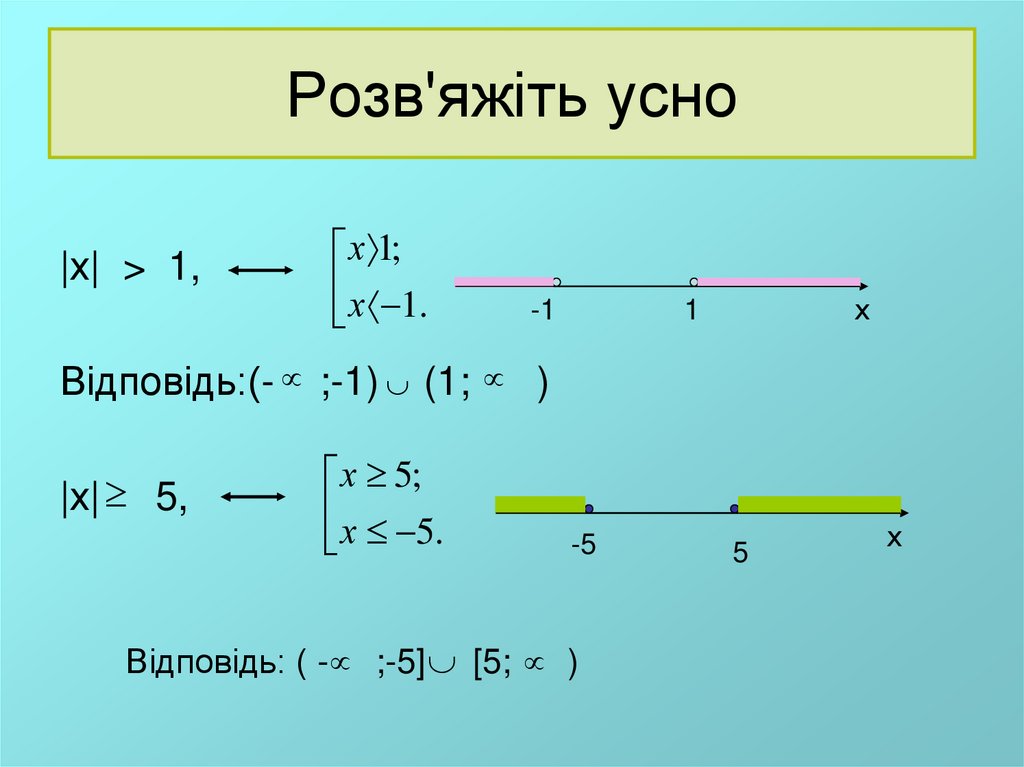
9. Розв'яжіть усно

|х| > 1,
х 1;
х 1.
-1
х
1
Відповідь:(- ;-1) (1; )
|х| 5,
х 5;
х 5.
-5
Відповідь: ( - ;-5] [5; )
5
х

10.

Розв'язати нерівності усно
|х| < -7,
|х| -76,
|х| >-32,
|х| -6

11.

Приклади:
|х|< 2,
|х| 4
-2<х<2,
(-2;2).
-2
2
-4
х
х 4, або [-4;4].
-4
4
х

12. Колективне розв'язання: |2x-3|<5.

Колективне розв'язання: |2x-3|<5.
Розв'язання :
|2x-3|<5.
-5<2x-3<5,
-5+3<2x-3+3<5+3,
-2<2x<8,
-1<x<4.
Геометрична інтерпретація:
Відповідь: х (-1; 4).

13. Колективне розв'язання: |x-2|>3.

Колективне розв'язання: |x-2|>3.
Розв'язання:
|x-2|>3,
x 2 3;
x 2 3,
x 3 2;
x 3 2,
Геометрична інтерпретація:
Відповідь: х (-∞; -1) (5; ∞).
x 5;
x 1,

14.

15.

16.

Метод інтервалів
Роза'язати нерівність |х+2| +|х-2|< 6
Знайдемо значення х, для яких значення виразів, які стоять під
знаком модуля, дорівнюють нулю:
Х+2 = 0 , х = -2
і
х – 2 = 0, х = 2
Значення х=-2 і х=2 розбивають координатну пряму на три проміжки.
-2
х
2
1.х< -2,
Дана нерівність набуде вигляду: -х-2-х+2<6,
враховуючи , що х< -2 , маємо систему
-2х<6, х>-3, але
Х >-3;
х< -2, тобто хє (-3;-2)

17.

|х+2| +|х-2|< 6
2.
-2 х 2
Дана нерівність набуде вигляду:
Х+2 –х+2<6, 0х+4<6, 0х<2.
3. х > 2.
Немає розв'язків.
Дана нерівність набуде вигляду:
Х+2+х-2< 6, 2х< 6, х< 3.
Враховуючи
х >2 маємо систему:
х< 3
х>2
2
(2;3)
Відповідь:
(-3;-2) (2;3)
3
х

18. Схема розв'язування нерівностей методом інтервалів

1.Знайти значення х, при яких підмодульні вирази дорівнюють
нулю.
2.Нанести знайдені значення на координатну пряму.
3.Методом пробної точки розкрити модулі і розв'язати
дану нерівність на кожному з утворених проміжків.
4.Отримані розв'язки на кожному з проміжків
об'єднати.

19.

Колективне розв'язання: |x-1|+2х<5.
Розв'язання :
|x-1|+2х<5.
За означенням модуля числа, якщо:1) х-1 0, то маємо х -1 +2х < 5, тобто
має місце система: x 1 0;
x 1 2 x 5.
x 1 0;
2)х-1< 0, то –(х-1)+2х<5 , тобто має місце система:
( x 1) 2 x 5.
Тому дана нерівність рівносильна сукупності двох систем нерівностей:
x 1 0;
x 1 0;
і ( x 1) 2 x 5;
Розв'яжемо кожну з них.
x
1
2
x
5
;
x 1;
x 1;
x 1 2 x 5.
і
3x 6;
x 1;
x 1;
(- ;1)
х<1.
і
x
1
;
x
4
;
x 1 2 x 5;
x 2.
[1;2)
Відповідь. х (-∞; 2).
1
2
х

20. Самостійна робота