Стандартные распределения непрерывной случайной величины. Теория вероятности и математическая статистика

1.

Стандартные
распределения
непрерывной случайной
величины
Теория вероятности и математическая
статистика

2.

Цель урока
Формирование
знаний
о
равномерно
распределенных
непрерывных
случайных
величинах и их числовых характеристиках.

3.

Повторение
Числовая величина значение которой может меняться в
зависимости от результата эксперимента называется …
случайной
2. Случайная величина, принимающая конечное множество
значений, называется …
дискретной
3. Случайная величина, значения которой принадлежит
интервалу (конечному или бесконечному) называется …
непрерывной
1.

4.

Указать непрерывные случайные величины?
1. Число выпавших очков игральной кости
2. Вес наудачу выбранного ученика
3. Оценка за контрольную работу
4. Число учеников, отсутствующих в классе
5. Расстояние, которое пролетит снаряд при выстреле
Ответ: 2, 5

5.

Повторение
Чем можно задать непрерывную случайную величину?
a) Функцией распределения F (x )
b) Функцией плотности распределения f (x )
c) Математическим ожиданием M (x)
d) Дисперсией D(x)
f ( x) F ( x)

6.

Обзор стандартных распределений
Непрерывные
случайные величины
Равномерное
распределение
Показательное
распределение
Нормальное
распределение

7.

Равномерное распределение
Определение:
Непрерывная
случайная
величина
Х
имеет
равномерное
распределение на отрезке [а, в], если на этом отрезке плотность
распределения вероятности случайной величины постоянна, т.е.
если функция плотности распределения f(х) имеет следующий вид:
С , если x [a, b]
f ( x)
0, если x [a, b]

8.

Равномерное распределение
С , если x [a, b]
f ( x)
0, если x [a, b]
Как найти число С?
f ( x)dx 1
bb
bb
aa
aa
bb
Сdx CC dx
dx Cx
Cx| | CC((bb aa)) 11
ff((xx))dxdx Сdx
aa
b
b
a
a
b
Сdx C dx Cx | C (b a) 1
a
a
1
C
b a

9.

Плотность распределения
1
, если x [a, b]
f ( x) b a
0 , если x [a, b]
Как найти функцию распределения F(x)?
x
F ( x) f (t )dt
f (x )
a
b
x

10.

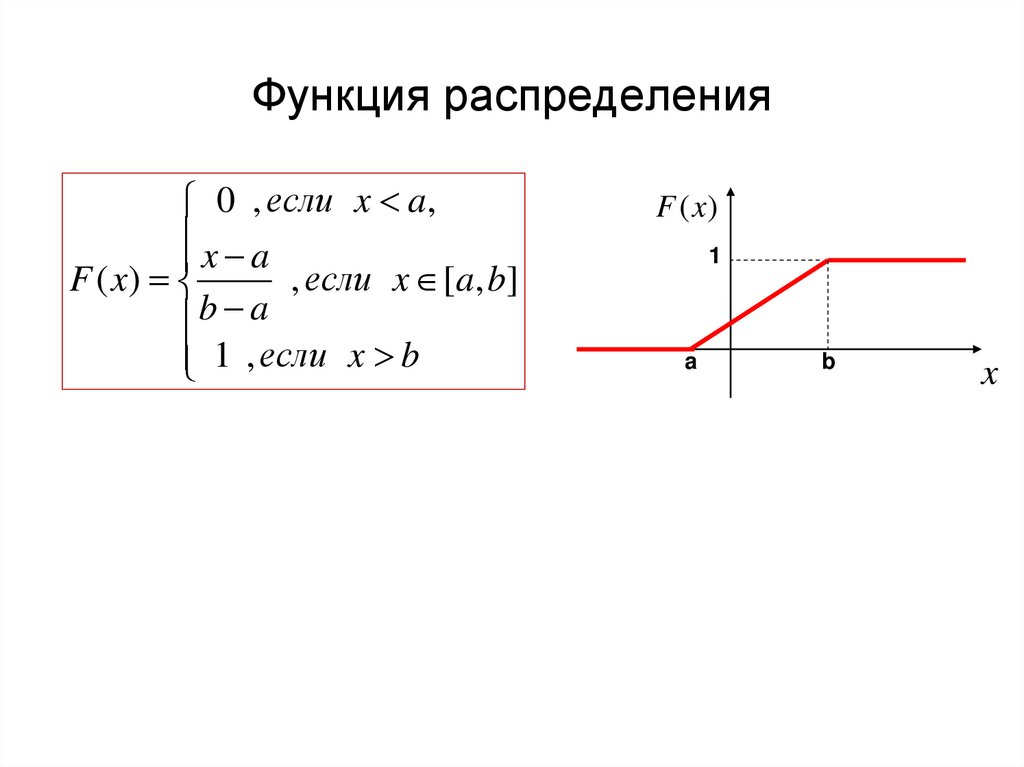
Функция распределения
0 , если x a,
x a
F ( x)
, если x [a, b]
b a
1 , если x b
F (x )
1
a
b
x

11.

Числовые характеристики равномерной
непрерывной случайной величины

12.

Математическое ожидание
Как найти математическое ожидание непрерывной величины?
1
, если x [a, b]
f ( x) b a
0 , если x [a, b]
M ( X ) x f ( x) dx
x
1
1 x2 b b2 a2
M ( X ) x f ( x) dx
dx
x dx
|a
b a
b a a
b a 2
2 b a
a
b
b
(b a)(b a) (b a)
2(b a)
2
M (X )
a b
2

13.

Дисперсия
Как найти дисперсию непрерывной величины?
2
x
a b
D( X ) x 2 f ( x) dx ( M ( X )) 2
dx
b a
2
a
2
b
3 b
2
3
2
1
(
a
b
)
1
x
(
a
b
)
(
b
a
)
(
a
b
)
2
x
dx
b a a
4
b a 3 a
4
3 b a
4
b
2
(b a )(b 2 ab a 2 ) a 2 2ab b 2 b 2 ab a 2 a 2 2ab b 2
3 b a
4
3
4
4b 2 4ab 4a 2 3a 2 6ab 3b 2 ab 2 2ab ab 2 (ba ab)) 2
12
12
12
12
2
(b a) 2
D( X )
12
2
2

14.

Числовые характеристики
Математическое ожидание
Дисперсия
a b
M (X )
2
(b a) 2
D( X )
12
Среднеквадратическое отклонение
b a
2 3
X ( , )

15.

Вероятность попасть в интервал (α,β)
dx
1
x
P( x ) f ( x)dx
dx
b
a
b
a
b a b a
P( x )
b a
Числа a и b называются параметрами распределения и они
однозначно определяют равномерное распределение.

16.

Учим формулы
Константа плотности
Дисперсия
Математическое ожидание
P( x )
M (X )
b a
1
b a
D(X )
a b
2
Среднеквадратичное
отклонение
Вероятность попадания
в интервал
b a
2 3
(b a) 2
C
12

17.

Задача 1
Непрерывная случайная величина задана плотностью
вероятности
С , если x [1,5]
f ( x)
0, если x [1,5]
Вычислить константу C, математическое ожидание,
дисперсию и среднее квадратичное отклонение.

18.

Решение
С , если x [1,5]
f ( x)
0, если x [1,5]
1
1
C
b a 4
a b 1 5
M (X )
3
2
2
(b a) 2 (5 1) 2 4
D( X )
12
12
3
b a
2
2 3
3
(5 1) 2 4 2
Ответ: 0,25; 3; ; 3
12
3

19.

Самостоятельная работа на 5 минут
Непрерывная случайная величина задана плотностью вероятности
A, если x [1,8]
f ( x)
0, если x [1,8]
Вычислить константу A, математическое ожидание, дисперсию и
среднее квадратичное отклонение.

20.

Задача 3

21.

Задача 4

22.

Домашнее задание