Похожие презентации:
Числовые и функциональные ряды
1. Числовые и функциональные ряды
Кулиш Н.В.,доцент
кафедры прикладной
математики
2.
1.1 Понятие числового рядаСходимость и расходимость рядов
• Понятие числового ряда
• Пример
• Теорема 2(сравнения)
• Теорема 3(сравнения)
• Интегральный признак сходимости
• Общий признак Даламбера
• Предельный признак Даламбера
• Общий признак Коши
• Предельный признак Коши
• Функциональные ряды
В конец
3. Понятие числового ряда Сходимость и расходимость рядов
Перейти к началуПонятие числового ряда
Сходимость и расходимость
рядов
Пусть дана числовая
последовательность
u n
Выражение un u1 u2 ... un ...(1) называется числовым
n 1
рядом
Числа u1, u2,…un…-члены
последовательности, un-n –й член ряда.
n
Рассмотрим сумму n первых S n u k -частичная сумма
k 1
ряда (1) .
S1 u1 , S2 u1 u2 ,...Sn u1 u2 ... un ,...
S n последовательность частичных сумм.
Определение: Если существует lim S n S ,то ряд
n
сходится, S –сумма. В противном
случае –расходится.
В конец
4. Понятие числового ряда
• Если члены ряда положительны, то егоназ. рядом с положительными членами
• k N : U 0
n
• Если знаки членов ряда чередуются :
u1 u2 u3 ... ( 1) k 1 un ......( k N : U k 0)
• то ряд наз. знакочередующимся.
5. Понятие числового ряда
• Если знаки членов ряда чередуютсяпроизвольно , то ряд наз.
знакопеременным(с произвольными
знаками)
6.
Перейти к началуПример1
4
4
4
4
...
...
1* 3 3 * 5 5 * 7
(2n 1)(2n 1)
1
1
4
2(
)
2n 1 2n 1 (2n 1)( 2n 1)
1
1 1
1 1
S 2(1 ) 2( ) 2( ) .... 2
3
3 5
5 7
В конец
7.
Перейти к началу• Пример2 Геометрическая прогрессия
a ax ax ax ... ax ...
2
3
n
n 1
S n a ax ax ... ax
2
3
n
S n x ax ax ax ax
2
a(1 x )
S n S n x a ax S n
1 x
n
n
В конец
8.
Перейти к началуa
lim S n
n
1 x
При IxI<1
При IxI>1
Sn
При IxI=1
Sn (n 1)a
X=1
X=-1
a , n 2 k 1
Sn
0, n 2k
В конец
9. Свойства сходящихся рядов
Перейти к началуСвойства сходящихся рядов
Теорема1
Если ряд сходится , то прибавление и
отбрасывание конечного числа членов не
влияет на сходимость ряда.
Доказательство
Пусть сумма отброшенных членов Ck
S n Ck n k
lim S n S , lim Ck Ck
n
n
lim n k S Ck
n
В конец
10. Свойства сходящихся рядов
Перейти к началуСвойства сходящихся рядов
Теорема2
Если ряд (1) сходится и его сумма S, то
сходится ряд (2)
Cu1 Cu2 ...Cun ...
и сумма его равна CS.
Теорема3Если сходятся ряды u1 u2 u3 ... un ...(1)
и v1 v2 ... vn ...(3) и суммы их равны
соответственно S1uS 2 то сходятся ряды
(u1 v1 ) (u2 v2 ) ... (un vn ) ...
И суммы их равны
S1 S 2
В конец
11. Необходимые признаки сходимости
Перейти к началуНеобходимые признаки
сходимости
Теорема1 Если ряд (1) сходится, то предел его
общего члена lim u 0
n
n
Д-во
S n 1 S
Пусть ряд (1) сходится, lim S n S , lim
n
n
lim u n lim ( S n S n 1 ) S S 0
n
n
Cледствие.Если
то ряд расходится.
lim u n 0
n
В конец
12. Необходимые признаки сходимости
Перейти к началуНеобходимые признаки
сходимости
Замечание Существуют расходящиеся ряды,
общий член которых стремится к нулю.
1 1 1
1
Это гармонический ряд
1 ... ...
2 3 4
n
он расходится
Пример1
3 5
2n 1
...
....
4 6
2n 2
2n 1
lim
1 0
n 2n 2
В конец
13. Необходимые признаки сходимости
Перейти к началуНеобходимые признаки
сходимости
Теорема 2 Если ряд (1) сходится, то
последовательность его частичных сумм
ограничена.
M 0 : n : Sn M
В конец
14. Необходимые признаки сходимости
Перейти к началуНеобходимые признаки
сходимости
Замечание1
Существуют расходящиеся ряды,
последовательность частичных сумм
которых ограничена
Пример: 1-1+1-1+….+…
Замечание2
Если ряд (1) состоит из положительных членов,
то из т2 следует его сходимость.
В конец
15. Ряды с положительными членами
Перейти к началуРяды с положительными
членами
I Признаки, основанные на сравнении
u , u 0, k N ...(1)
k 1
k
k
v , v 0, k N ...(2)
k
k
k 1
Теорема1 Если
члены ряда (1) не
превышают соответствующих членов
ряда(2), то из сходимости ряда (2)
следует сходимость ряда (1), из
расходимости ряда (1) следует
расходимость ряда (2).
В конец
16. Доказательство
Перейти к началуДоказательство
Пусть выполнено u v ...(3).. n. N
n
n
Положим S n u n
Соответственно частичные суммы рядов (1) и
n
n
(2)
S n u k , n vk
k 1
k 1
Из (3) S n vn ..(4)
n
Т.к. (2) сходится, то lim
n
n ... n N ... S n n
Т.е. S n Возрастает и ограничена сверху
В конец
17. Доказательство
Перейти к началуДоказательство
Sn S
Следовательно .. lim
n
Если ряд (1) расходится, то из
положительности членов ряда
lim S n ,... lim n
n
из (4)
n
В конец
18. Примеры
Перейти к началуПримеры
Установить сходимость или расходимость
рядов
1) 1 1 1 ... 1 .....(1)
2
3
n
1 1
1
1 ... .....(2)
2 3
n
1
1
n
n
т.к. расх. ряд(2), то расх-ся и ряд(1)
В конец
19. Примеры
Перейти к началуПримеры
2)
1
1
1
1 2 3 ... n ...(1)
2
3
n
1
1
1
1 2 3 ... n ...( 2)
2
2
2
1
1
n
n
n
2
Т.к. ряд (2) сх-ся, то ряд (1) сходится
В конец
20. Теорема2
Перейти к началуТеорема2
2) Если для рядов с положительными
un
членами (1) и (2)
lim
conct
n v
то либо оба ряда
n
сходятся, либо оба ряда расходятся
В конец
21. Пример
Перейти к началуПример
1) Исследовать на сходимость
1
;....
n 1 5n 2
1 1
1* n
1
lim
: lim
const
n 5n 2 n
n (5n 2) *1
5
Т.к. гармонический ряд расходится, то
расходится и данный ряд
В конец
22. II Признак Даламбера
Перейти к началуII
Признак Даламбера
Если в ряде с положительными
членами lim u n 1 l
n
un
То при l<1 ряд сходится,
при l>1 ряд расходится,
при l=1 признак не дает ответ на
вопрос о сходимости ряда.
В конец
23. Доказательство
Перейти к началуДоказательство
1)Пусть
u n 1
lim
l 1
n u
n
q : ...l q 1
1 l
q
2
l q
u n 1
N : ( n N )
l q
un
В конец
24. Доказательство
Перейти к началуДоказательство
u N 1
uN 2
u N 3
q;
q;
q;...
uN
u N 1
uN 2
u N 2 qu N 1; u N 3 qu N 2 q u N 1...
2
В конец
25. Рассмотрим ряд
Перейти к началуРассмотрим ряд
u u
k N 1
k
N 1
u N 2 u N 3 .....(1)
И ряд u N 1 qu N 1 q u N 1 .... q u N 1 .....(2)
2
k
Ряд (2) сходится как геометрическая
прогрессия, а значит сходится ряд (1),
т.к. прибавление и отбрасывание
конечного числа членов не влияет на
сходимость ряда
В конец
26.
Перейти к началу2) Пусть
un 1
un 1
lim
l 1 0( N ) : ( n N )
1
n u
un
n
: l 1
u N 1 u N ; u N 2 u N 1 ; u N 3 u N 2 .....
u N 1 u N 2 u N 3 ..... u N k ...(3)
u N 1 u N 2 u N 3 ......
В конец
27. значит ряд(3)
Перейти к началузначит ряд(3)
расходится , т.к. предел общего члена не
равен 0 .
значит расходится и ряд (1)
3) Пусть
u n 1
lim
1
n
un
Тогда признак Даламбера не дает ответ на
вопрос о сходимости ряда.
u n 1
1
Но, если
то ряд расходится
un
т.к. общий член ряда не стремится к 0
В конец
28. Примеры
Перейти к началуПримеры
1
1 1
1
1) 1 ... ...
2! 3!
n!
n 1 n!
1
1
un ; un 1
;
n!
(n 1)!
un 1
1
1
n!
n!
1
:
0
un (n 1)! n! (n 1)! n!(n 1) n 1
0<1, значит ряд сходится
В конец
29. Примеры
Перейти к началуПримеры
2 * 5 * 8 * ...(3n 1)
2 *5*8
...
...
2
1* 5 * 9 * ...(4n 3)
1* 5 1* 5 * 9
2 * 5 * 8 * ...(3n 1)(3n 2)
2 * 5 * 8 * ... * (3n 1)
;
; un 1
un
1* 5 * 9 * ...(4n 3)( 4n 1)
1* 5 * 9 * ...(4n 3)
un 1 3n 2 3
1 cx.
u n 4n 1 4
2) 2 * 5
В конец
30. Примеры
Перейти к началуПримеры
3)tg 2tg 3tg ... ntg n 1 ...
4
8
16
2
un ntg n 1 ; un 1 (n 1)tg n 2
2
2
tg n 2
tg n 2
tg n 2
un 1 n 1 2
n 1 2
n 1
2
un
n tg
n tg 2
n 2tg
2 n 1
2n 2
2n 2
2
1 tg n 2
2
В конец
31.
Перейти к началуn 1
n
(1 tg
2
2
2
n 2
)
n 1
1
2
(1 tg n 2 ) 1 cx.
2n
2
2
В конец
32. Примеры
Перейти к началуПримеры
4)
n
n
n 1
8
2
2
2
2 1 ... 2 ...; un 2 ; un 1
2
9
n
n
(n 1)
n 1
2
un 1
2
n
lim
lim
2 *1 2 1
2
n
n u
n ( n 1) 2
n
расходится
В конец
33. Примеры
Перейти к началуПримеры
5)
1 2 3
n
n
n 1
...
...; un
; un 1
;
2 3 4
n 1
n 1
n 2
2
2
un 1 (n 1) (n 1) (n 1)
un 1 n 2n 1
1; 2
1
un (n 2) n n(n 2)
un
n 2n
расходится
В конец
34. Радикальный признак Коши
Перейти к началуРадикальный признак Коши
Т.1
Если для ряда с положит. членами
существует конечный lim n u n
n
То
при l<1 ряд сходится,
при l>1 ряд расходится,
при l=1 нужны дополнительные
исследования (без д-ва)
В конец
35. Исследовать на сходимость
Перейти к началуИсследовать на сходимость
1)
1 22 33
n n
( ) ( ) ... (
) ...
3 5
7
2n 1
n
n
1
n
lim n un lim n (
) lim
1 cx.
n
n
2n 1 n 2n 1 2
В конец
36. Исследовать на сходимость
Перейти к началуИсследовать на сходимость
2)
2 1 34
1 n 1 n2
1
n
1
n
n
( ) ... n (
) ....... un (
)
3 9 2
3 n
3 n
1
1 n 1
n
lim un lim (1 ) e 1 cx.
n
3 n n
3
В конец
37. Интегральный признак сходимости
Перейти к началуИнтегральный признак
сходимости
Т 2.
Пусть члены ряда (1) положительны и не
возрастают, т.е. u1 u2 u3 ... un ...
И функция f(x)-непрерывная,
невозрастающая функция такая, что
f (1) u1; f (2) u2 ;... f (n) un ;....
Тогда 1)
1 f ( x )dx сходится, то ряд
сходится
2) f ( x ) dx расходится, то ряд расходится
1
В конец
38. Исследовать на сходимость
Перейти к началуИсследовать на сходимость
1
1
1 1
1 p p ... p ...;.. p 0;.. f ( x) p ;1) p 1
x
n
2 3
b
b
1
dx
1
1 p
p
lim x
lim x dx
p
1 x p dx blim
b
b
x
p
1
1
1
a) p 1 cx; b) p 1; pacx; c) p 1; lim ln n
n
В конец
39. Знакочередующиеся ряды
Перейти к началуЗнакочередующиеся ряды
Т. Лейбница
Если в знакочередующемся ряде члены не
возрастают и предел общего члена
равен нулю, то ряд сходится, сумма его
положительна и не превышает его
первого члена.Знакочередующийся ряд
n 1
u1 u2 u3 ... ( 1) un .......(1); un 0( n N )
Рассм-м четные и нечетные суммы ряда
В конец
40. Доказательство
Перейти к началуДоказательство
u1 u2 u3 ... un ....
S 2 m (u1 u2 ) (u3 u4 ) .... (u2 m 1 u2 m ) 0...u.bo3 pacmaem
S 2 m u1 (u2 u3 ) (u4 u5 ) ... u1 lim S 2 m S
n
0 S u1; lim S 2 m 1 lim ( S 2 m u2 m 1 ) S 0 S
n
n
В конец
41. Остаток ряда
Перейти к началуОстаток ряда
u1 u2 u3 ... ( 1) n 1 un .......(1); un 0( n N )
k n 1
k n 1
S S n uk S n rn ;..rn uk ; rn un 1
В конец
42. Примеры
Перейти к началуПримеры
2n
( 1)
n
(
4
n
1
)
5
n 1
n
1) Сколько членов ряда
нужно взять, чтобы вычислить его сумму с
точностью до 0,001?
2n
2
4
6
8
n
lim un 0; ( 1)
...
n
n
(4n 1)5
25 225 13 *125 1250
S3 u1 u2 u3 S
В конец
43. Оценить ошибку
Перейти к началуОценить ошибку
1
Допускаемую при замене суммы ряда ( 1)
n
n 1
суммой его первых n членов
n
Оценить погрешность приближения при
n=11
1
1
u n 1
; n 11; u n 1
0,1
n 1
12
В конец
44. Знакопеременные ряды абсолютная и условная сходимость
u ( 2)Перейти к началу
k
Знакопеременный ряд
k 1
Т.1.Если знакопеременный ряд таков, что
сходится ряд, составленный из
абсолютных величин членов ряда, то и
данный ряд сходится.
Доказательство u k u1 u 2 ... u n ...(3)
k 1
Пусть S n частичная сумма ряда (2)
n частичная сумма ряда (3)
В конец
45. Сумма положительных и суммамодулей отрицательных членов в частичной сумме
S nПерейти к началу
соответственно
I
n
S uS
S n S S ; n S S
I
n
II
n
I
n
II
n
II
n
n ; S 0; S 0возрастают сходятся
I
n
II
n
S S ;S S n S S
I
n
I
II
n
II
I
II
S n S S S ч.т.д.
I
II
В конец
46. Замечание
Перейти к началуЗамечание
Существует много рядов, которые сходятся,
а ряды, составленные из абсолютных
величин их членов расходятся
1 1 1
1 1 1
1 ....и1 .....
2 3 4
2 3 4
В конец
47. О.1 Знакопеременный ряд(2) наз.абсолютно сходящимся, если сходится ряд (3)
Перейти к началуО.1 Знакопеременный ряд(2)
наз.абсолютно сходящимся,
если сходится ряд (3)
О.2 Если ряд (2) сходится, а ряд (3)
расходится, то ряд (2) наз. условно
сходящимся
Т.2.Если ряд сх-ся абсолютно, то он
остается абсолютно сходящимся при
любой перестановке его членов. При
этом сумма ряда не зависит от порядка
его членов.
В конец
48.
Перейти к началуТ.3.
Если ряд сходится условно, то какое бы
число А ни взяли, можно так
переставить члены этого ряда , что он
останется сходящимся и его сумма будет
равна А. Более того, можно сделать
такую перестановку его членов, что он
будет расходиться.
В конец
49. Функциональные ряды
Перейти к началуФункциональные ряды
u1 ( x) u 2 ( x) ... u n ( x) .... u n ( x )....(1)
Ряд
n 1
наз. функциональным, т.к. членами ряда
служат функции ui ( x); i 1,2,.....
Придавая x фиксированное значение, мы
обращаем функциональный ряд в
числовой, для которого уже можно
применять признаки сходимости.
Совокупность значений x , для которых ряд
(1) сходится, наз. областью сходимости
этого ряда.
В конец
50. Пример 1. определить область сходимости ряда(абсолютной и условной)
Перейти к началу( 1) n 1 x n
1 1 x 2
1 x
) ......( 2)
(
) ...
) (
(
2n 1 1 x
3 1 x
1 x
составим... ряд.( 2* )..из..абс.величин
2n 1
1 x
2n 1 (1 x) n 1 (1 x) n
lim
lim
lim
n
1
n
n 2n 1 (1 x )
n u ( x )
1 x n 2n 1
(1 x)
n
u n 1 ( x)
1 x
1 x
В конец
51.
Перейти к началу1 x
npu..x 0
1 (2)u (2* ) pacx
1 x
1 x
npu..x 0
1 (2* )cx (2)cx..абсолютно
1 x
1 1
npu..x 0 : 1 ....сх..т.Лейбница
3 5
1 1
*
но.. ряд.из.абс.величин(2 )...1 .... расх. ( 2)сх. условно
3 5
В конец
52. Вывод
Перейти к началуВывод
Область сходимости
0 x
на..промежутке0 x ...абсолютно.сх.
В конец
53. Пример 2
Перейти к началуПример 2
xn
2n
1
x
n 1
lim
n
x
n 1
1 x
2n
1 x 2n 2 x n
x (1 x 2 n )
lim
n 1 x 2 n 2
В конец
54.
Перейти к началуx(1 x 2 n )
x 1 lim
x 1 абс.сх ся
2
n
2
n 1 x
1
1
2n
2
n
1
1 x
1
x
x
x 1 lim
lim
1 cx
n 2 n 1
n
1
1
x
x (1 2 n 2
1 2n 2
x
x
1
n 1 2
x 1
n расх ся , D : ( ; 1) ( 1;1) (1; ) абс
( 1)
2
n 1
В конец
55.
Перейти к началуn
S n ( x) u k ( x).частичная.сумма. ряда (1)
k 1
rn u k ( x) u n 1 u n 2 ....остаток. ряда (1)
k n 1
если. ряд (1).сх ся.и.S ( x).его..сумма , то
S ( x) S n ( x) rn ( x) lim S n ( x) S ( x)
n
lim rn ( x) lim ( S ( x) S n ( x) S ( x) S ( x) 0
n
n
В конец
56. Вывод: если x т. сх-сти ряда, то остаток ряда стремится к нулю
Перейти к началуО.
Функциональный ряд наз. мажорируемым в
некоторой области изменения x, если
существует сходящийся числовой ряд с
положительными членами 1 2 ... n .....(3)
Такой, что для всех x из этой области и при
любом n un ( x) n
Ряд (3) наз.мажорантой ряда (1)
В конец
57. Степенные ряды
Перейти к началуСтепенные ряды
О.
Функциональный ряд вида
a x a a x a x ... a x ....(4)
n
n 0
n
2
0
1
2
n
n
наз. степенным рядом.
Эти ряды всегда сходятся в точке x=0,т.е.
область сходимости степенного ряда е
является пустой.
Коэффициенты степенного ряда
В конец
58. Теорема Абеля
Перейти к началуТеорема Абеля
Если степенной ряд (4) сходится в
некоторой точке x0 , то он абсолютно
сходится в любой точке x, такой , что
x x0
Если ряд (4) расходится в точке x0 , то он
расходится в любой точке x такой, что
x x0
В конец
59. Доказательство:
Перейти к началуДоказательство:
По условию сходится
2
n
a0 a1 x0 a2 x0 ... an x0 ....(5)
тогда
n
n
lim an x0 0 0( N 0 ) : ( n N 0 ) an x0
n
выберем..наибольшее..среди.конечного..числа..чисел
2
max( a0 ; a1 x0 ; a2 x0 ;.... a N 0 x0
N0
; ) K an x0 K ( n N )
n
a0 a1 x a2 x 2 a3 x 3 ... an x n ...(6)
x
2 x 2
n x n
ряд (4) (6 ) : a0 a1 x0 a2 x0 ( ) ... an x0 ( ) ...
x0
x0
x0
I
2
n
x
2 x
n x
a0 a1 x0
a2 x0
... an x0
...(7)
x0
x0
x0
В конец
60. Доказательство:
Перейти к началуK K
2
n
Доказательство:
x
x
x
x0
K
x0
... K
.....(8)
x0
x
q
1 : ..K Kq Kq 2 ... Kq n ...(9)
x0
2) Пусть ряд (4) расходится в т. x0 ,
рассмотрим точки x: x x
0
Если предположить , что ряд сходится
в точке x тогда он должен сходиться в т. x0
А это противоречит условию. Ч.т.д.
В конец
61. Замечание:
Перейти к началуЗамечание:
Из доказанной т-мы следует, что
R 0 : ( x : x R) ряд (4)сх ся
( x : x R) (4) расх ся
интервал( R; R) интервал..сх сти
R радиус..сх сти
В конец
62. Для определения радиуса сх-сти воспользуемся признаком Даламбера:
Для определения радиуса схсти воспользуемся признакомДаламбера:
Перейти к началу
n 1
an 1 x
lim
n a x n
n
an 1
x lim
1
n a
n
an
an
x lim
R lim
n a
n a
n 1
n 1
в.точках...x R.u.x R..сх сть.. ряда (4)
устанавливается.особо
В конец
63. Пример 1
Перейти к началуПример 1
n
(2 x) 2 (2 x) 3
(
2
x
)
2x
... ( 1) n 1
...
2
3
n
u n 1
( 2 x) n 1 n
lim
lim
2 x 1
n
n u
n ( n 1)( 2 x )
n
1
1
1
x x
2
2
2
1
1 1
1
1
1
x 1 ... ... (1 ... ...) расх
2
2 3
n
2
n
1
1 1
n 1 1
x 1 ... ( 1)
... сх. условно
2
2 3
n
1 1
ответ : область.сх сти ;
2 2
В конец
64. Пример 2
Перейти к началуПример 2
n
9 2n
x sin( 3x n)
n 1 2n
un 1
9 x
sin( 3x n )2n
2
lim
lim
9x 1
n
2
n
n u
n 2( n 1)9 x
sin( 3x n)
n
n 1
2n 2
1
1
1
1
x x x
9
3
3
3
2
В конец
65. Проверим на границах интервала:
Перейти к началуПроверим на границах
интервала:
1 2n
n 1
9 ( )
9
n
1
1
x 3 sin( 3 * n ) 9 ( sin( 1 n))
3 n 1 2n
3
n 1 2n
n
sin( 1 n)
;
2n
n 1
sin( 1 n) sin 1cos n cos1sin n) sin 1cos n;
1 1 1
sin 1( ....) сх ся.. условно
2 4 6
В конец
66. Проверим на границах интервала:
Перейти к началуПроверим на границах
интервала:
1 2n
9 ( )
1
1
sin( 1 n)
3
x
sin( 3 * n ) (
)
3
2n
3
2n
n 1
n
sin 1cos n cos1sin n
сх ся.. условно
2n
n 1
1 1
ответ : ; область....сх сти
3 3
В конец
67. Пример 3:
Перейти к началуПример 3:
n 1
lim
n
n
3
n 1 n 1
un 1
3
x
n 1
; lim
lim
n n
2
2
n u
n
n 1
(n 1) 1 3 x
n
3
x
n
n n 1
1
x
n 1
lim
3
2
(n 1) 1 n
2
n n 1
n n 1
2
x x 1
1 x 1
В конец
68. На границах интервала:
Перейти к началуНа границах интервала:
3 n
n 1
n 1
x 1
3
1
dx
x
2
n 1
1
3
n
n 1
2
1
; но
3
n
n 1
2
1
3 n n
x
dx
3
2 x
2 lim 3 x d ( x ) 2 lim
b
b ln 3
2 x
x
1 3
1
b
1
2
2 1
2
b
1
lim (3 3 )
( )
сх ся
ln 3 b
ln 3 3
3 ln 3
x 1
3
n
( 1)
n
( 1)
n
знакочередующ ся
n
n 1 3
n2 1
n2 1
сх ся ответ : 1;1 обл сть....сх сти
n 1
В конец
69. Без доказательства сформулируем :
Перейти к началуБез доказательства
сформулируем :
Теорема 1
Cтепенной ряд мажорируем на любом
отрезке ; R; R и его сумма
непрерывна на этом отрезке.
Теорема 2
Степенной ряд можно почленно
интегрировать на промежутке сх-сти.
Теорема 3 Степенной ряд можно почленно
дифференцировать на промежутке схI
2
n 1
S
(
x
)
a
2
a
x
3
a
x
...
na
x
...
сти.
1
2
3
n
В конец
70. Ряды по степеням x-a
Перейти к началуРяды по степеням x-a
Рассмотрим ряд
n
2
n
a
(
x
a
)
a
a
(
x
a
)
a
(
x
a
)
...
a
(
x
a
)
...(1)
n
0
1
2
n
n 0
x a z a0 a1 z a2 z ... an z ... an z ...(2)
2
n
n
n 0
R 0 радиус...сх сти.. ряда (2) ( R; R)интервал..сх сти
( R z R) ( R x a R)
a R x a R интервал..сх сти(1)...( a R; a R)
В конец
71. Свойства степенных рядов по степеням x-a
Перейти к началуСвойства степенных рядов по
степеням x-a
Теорема1
Cумма степенного ряда(1) внутри его
интервала сх-сти является непрерывной
функцией.
Теорема 2
Ряд(1) можно почленно интегрировать на
его промежутке сх-сти.Полученный в
результате почленного интегрирования
ряд имеет тот же промежуток сх-сти, что
и ряд(1).
В конец
72. Свойства степенных рядов по степеням x-a
Перейти к началуСвойства степенных рядов по
степеням x-a
Теорема3
Cтепенной ряд внутри его промежутка схсти можно почленно дифференцировать
сколько угодно раз. Полученный при этом
ряд имеет тот же промежуток сх-сти, что
и ряд(1).
На практике интервал сх-сти степенного
ряда по степеням x-a можно находить с
помощью признака Даламбера.
В конец
73. Пример: найти область сх-сти
Перейти к началуПример: найти область сх-сти
x 2 ( x 2) 2 ( x 2) 3
( x 2) n
...
....
2
3
n
1* 2
2*2
3* 2
n2
( x 2) n 1 n 2 n
1
lim
x 2 1 x 2 2
n
n
(n 1) ( x 2)
2
( 2 x 1 2) (0 x 4) т.е. ряд..сх ся..абс.на (0,4)
( 2) n
( 1) n
x 0
сх ся.. усл.
n
n
n 1 n 2
n 1
1 1
ч 4 : 1 .... расх ся
2 3
ответ : 0;4
В конец
74. Разложение функции в степенные ряды.Единственность разложения
Перейти к началуРазложение функции в степенные
ряды.Единственность разложения
До сих пор, рассматривая тот или иной ряд, мы
устанавливали область его сходимости и
решали задачу о нахождении его суммы
S(x).Теперь рассмотрим обратную задачу:
Имеем функцию f(x) .Требуется найти такой
степенной ряд, который бы имел эту
функцию своей суммой в области
сходимости
В конец
75. определение
Перейти к началуопределение
Говорят, что функция f(x) разлагается на
данном промежутке L в степенной ряд, если
n
a
(
x
a
)
...(1)
существует такой степенной ряд n
n 0
Который на этом промежутке сх-ся к данной
функции так, что выполняется равенство
f ( x) a0 a1 ( x a) a2 ( x a) ... an ( x a) ...(3)
2
n
При этом говорят,что в промежутке L функция
f(x) разлагается в ряд по степеням ( x-a), а
правую часть равенства наз. разложением
функции f(x) по степеням ( x-a)
В конец
76.
Перейти к началуТеорема1
Если в некотором интервале, содержащем
данную точку a, функция f(x) имеет
разложение по формуле (3), то это
разложение единственно.
Доказательство
Пусть в интервале (a-R;a+R) имеет место
равенство (3), в котором коэффициенты
a0 , a1 , a2 ,....an ,...
нам не известны , пользуясь свойством
дифференцируемости степ.рядов
В конец
77. Доказательство
Перейти к началуДоказательство
Найдем эти коэф-ты, выразив их через данную
функцию f(x) и ее производные.
Т.к. f(x) в интервале (-R;R) есть сумма
степенного ряда, то она дифференцируема
любое число раз и
ее производные можно найти путем
почленного дифференцирования
степенного ряда
В конец
78. Доказательство
Перейти к началуДоказательство
f ( x) a0 a1 ( x a) a2 ( x a) 2 ... an ( x a) n ....
f I ( x) a1 2a2 ( x a) 3a3 ( x a) 2 ... nan ( x a) n 1 ...
f II ( x) 2a2 3 * 2a3 ( x a) ... n(n 1)an ( x a) n 2 ...
....
f ( n ) ( x) n(n 1)( n 2)...3 * 2 *1an (n 1)n(n 1)...( n n 1)an 1 ( x a) ...
В конец
79. Доказательство
Перейти к началуx a
Доказательство
f ( a ) a0
I
f
( a ) a1
f II ( a ) 1* 2a2
( 4)
..........
f ( n ) ( x) n( n 1)...2 *1an
..............
f I (a)
f II ( a )
f ( n ) (a)
( 4)......a0 f ( a ); a1
; a2
;...an
;...
1!
2!
n!
В конец
80. Таким образом
Перейти к началуТаким образом
Коэффициенты ряда (3) однозначно
определяются в (4)
Значит представление функции f(x) степенным
рядом единственно.
В конец
81. Ряды Тейлора
Перейти к началуРяды Тейлора
Пусть функция f(x) бесконечно
дифференцируема в т. a,тогда по
формулам (4) можно вычислить
коэффициенты, которые ей соответствуют
Определение
Степенной ряд с коэффициентами,
вычисленными по формулам(4),наз.рядом
Тейлора функции f(x) в окрестности точки
a(независимо от того, является функция f(x)
Его суммой или нет)
В конец
82. Т.е. ряд Тейлора имеет вид:
Перейти к началуТ.е. ряд Тейлора имеет вид:
I
II
(n)
f (a)
f (a)
f (a)
2
(5)... f (a)
( x a)
( x a) ...
( x a) n ...
1!
2!
n!
если...a 0, то.. ряд.........Маклорена
I
II
(n)
f (0) f (0) 2
f (0)
(6).... f (0)
x
x ...
...
1!
2!
n!
В конец
83. Таким образом
Перейти к началуТаким образом
Если функция в некоторой окрестности точки
А разлагается в степенной ряд, то этим рядом
непременно является ряд Тейлора
В конец
84. Остаток ряда
Перейти к началуОстаток ряда
Теорема1
Для того, чтобы ряд Тейлора (5) функции f(x)
сходился к ней в некотором интервале
(-R;R) , необх.и д., чтобы остаточный член Rn (x)
формулы Тейлора стремился к 0 при всех x
из того интервала, когда n неограниченно
возрастает.
f I (a)
f II (a)
f ( n ) (a)
2
f ( x) f (a)
( x a)
( x a ) ...
( x a) n Rn ( x)
1!
2!
n!
f I (a)
f II (a )
f ( n ) (a)
2
S n ( x) f (a )
( x a)
( x a) ...
( x a) n
1!
2!
n!
формула....Тейлора.принимает...вид. f ( x) S n ( x) Rn ( x)
В конец
85. Доказательство
Перейти к началуДоказательство
I . Необходимость
Дано : lim S n ( x) f ( x)..( x (a R; a R)д ть : lim Rn ( x) 0
n
lim ( f ( x) S n ( x)) 0, т.к. f ( x)не..зависит.от.n
n
lim Rn ( x) lim( f ( x) S n ( x)) 0
n
n
ч.т.д.
В конец
86. II. Достаточность
Перейти к началуII. Достаточность
Дано : lim Rn ( x) 0 lim ( f ( x) S n ( x)) 0
n
n
т.к. f ( x)не.зависит...от...п lim S n ( x) f ( x)
n
ч.т.д.
В конец
87. Доказанная теорема
Перейти к началуДоказанная теорема
Позволяет установить план решения задач на
разложение данной функции в ряд Тейлора
1) Найти производные функции f(x)
2) Вычислить значения производных в т.а
3) Записать формально ряд Тейлора
4) Найти интервал сходимости записанного
ряда
5) Записать остаточный член формулы
Тейлора
6) Найти множество значений x,для которых
В конец
остаточный член стремится к нулю
88.
Перейти к началу1) f I ( x), f II ( x),... f ( n ) ( x).....
2) f (a), f I (a), f II (a)... f ( n ) (a)...
f I (a)
f II (a)
f ( n ) (a)
2
3) f (a)
( x a)
( x a) ...
( x a) n ...
1!
2!
n!
f ( n 1) ( )
5) Rn
( x a) n 1 , a ( x a),0 1
(n 1)!
f I (a)
f II (a)
f ( n ) (a)
2
6) f ( x) f (a)
( x a)
( x a) ...
( x a) n Rn ( x)
1!
2!
n!
В конец
89. Разложим в ряд
Перейти к началуРазложим в ряд
1) f ( x) e x , a 0,
I
II
(n)
f
(
0
)
f
(
0
)
1
f
(0) 1
a0 f (0) e 0 1; a1
1; a2
;...an
...
1!
2!
2!
n!
n!
x x2
xn
1
...
....Признак.. Даламбера :
1! 2!
n!
un 1
x n 1 n!
1
lim
lim
x lim
0 1 ряд.сх ся x R
n u
n ( n 1)! x n
n n 1
n
e x
Rn ( x)
( x a) n 1 0 ряд..сх ся x R
(n 1)!
2
n
x
x
x
ex 1
...
....
1! 2!
n!
В конец
90.
Перейти к началу2 n 1
x3 x5
x
n
2) f ( x) sin x x ... ( 1)
...
3! 5!
(2n 1)!
2
4
2n
x
x
x
I
n
3) f ( x) cos x (sin x) 1 ... ( 1)
...
2! 4!
(2n)!
В конец
91. 4)Биномиальный ряд
Перейти к началу4)Биномиальный ряд
f ( x ) (1 x ) m , m R
m( m 1) 2 m( m 1)( m 2) 3
m
(1 x ) 1 mx
x
x ...
2!
3!
m( m 1)( m 2)...( m ( n 1)) n
x ....(1)
n!
1
m 1 :
1 x x 2 ... ( 1) n 1 x n ...( 2)
1 x
1
1
1
1* 3
2
m : 1 x 1 x
x
x 3 ...(3)
2
2
2*4
2*4*6
1
1
1
1* 3 2 1* 3 * 5 3
m :
1 x
x
x ...( 4)
2
2
2*4
2*4*6
1 x
В конец
92. Разложить в ряд
Перейти к началуРазложить в ряд
1
m 1 :
1 x x 2 x 3 ... ( 1) n 1 x n 1 ...(2)..( 1;1)
1 x
1
2
4
n 1 2 n 2
1 x x ... ( 1) x
...(3)...( 1;1)
2
1 x
x
x
dt
2
4
n 1 2 n 2
arctgx
(
1
t
t
...
(
1
)
t
...)dt
2
1 t
0
0
2 n 1
x3 x5
x
x ... ( 1) n 1
...(4).....( 1;1)
3 5
2n 1
В конец
93. При построении этого ряда Тейлора применили
Перейти к началуПри построении этого ряда
Тейлора применили
1)Замена x.на.x
2)Дифференцирование функции ( cosx )
3)Интегрирование при построении arctgx.
Эти приемы применяются для получения
разложений других функций
2
В конец





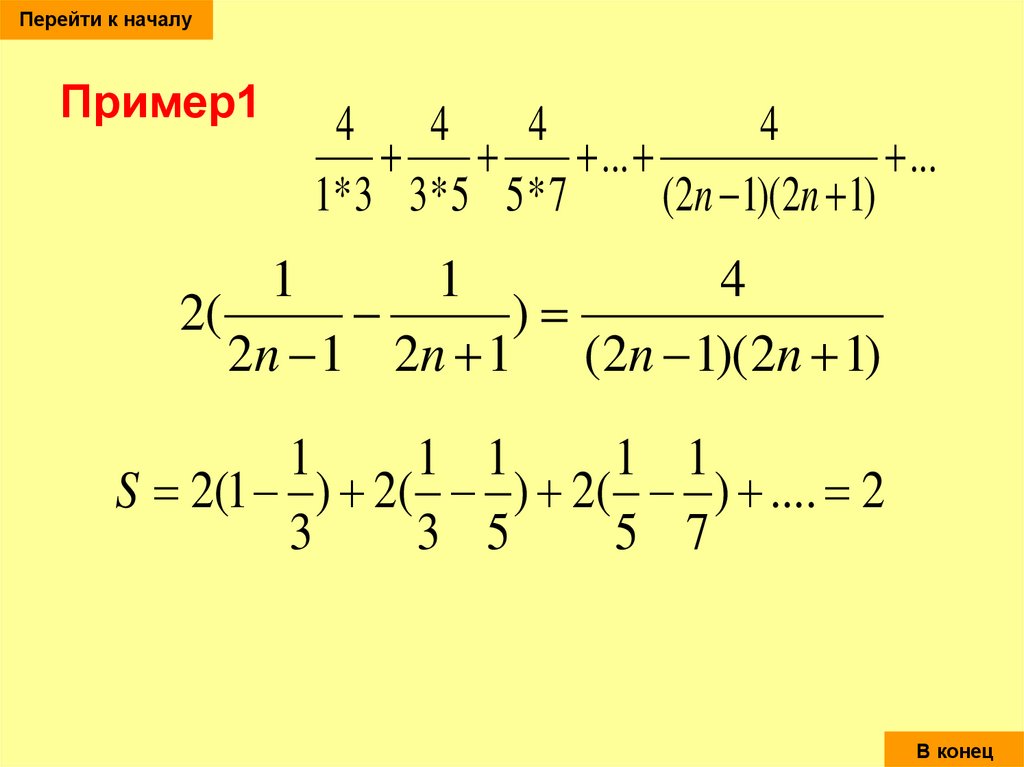
























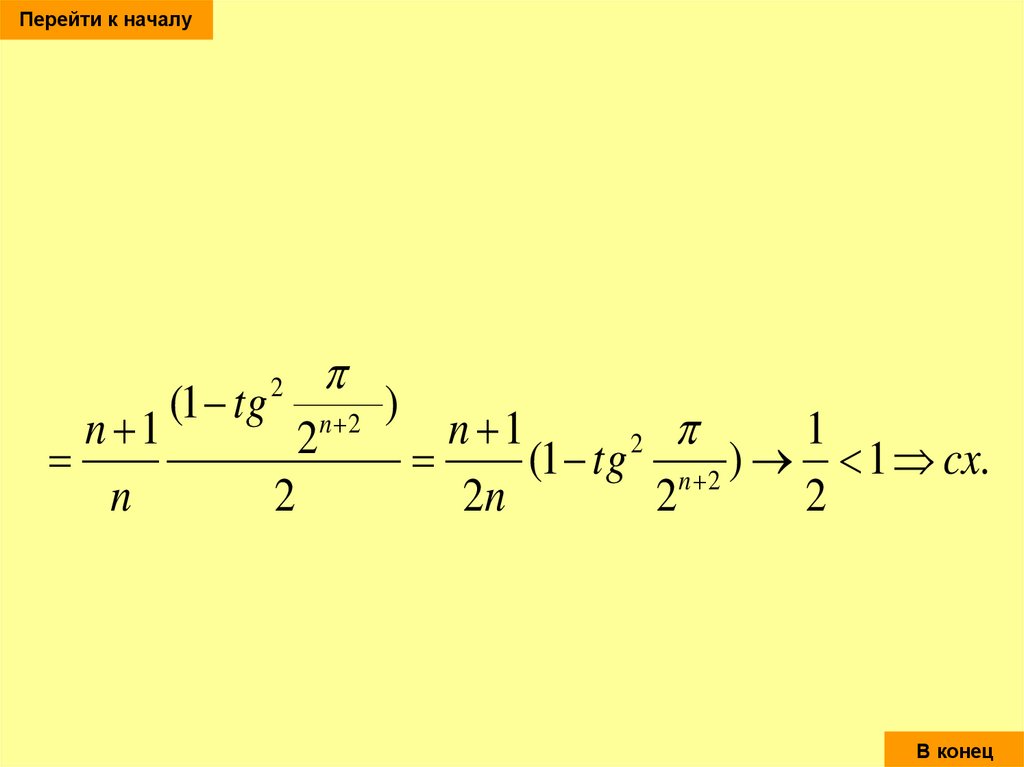
























































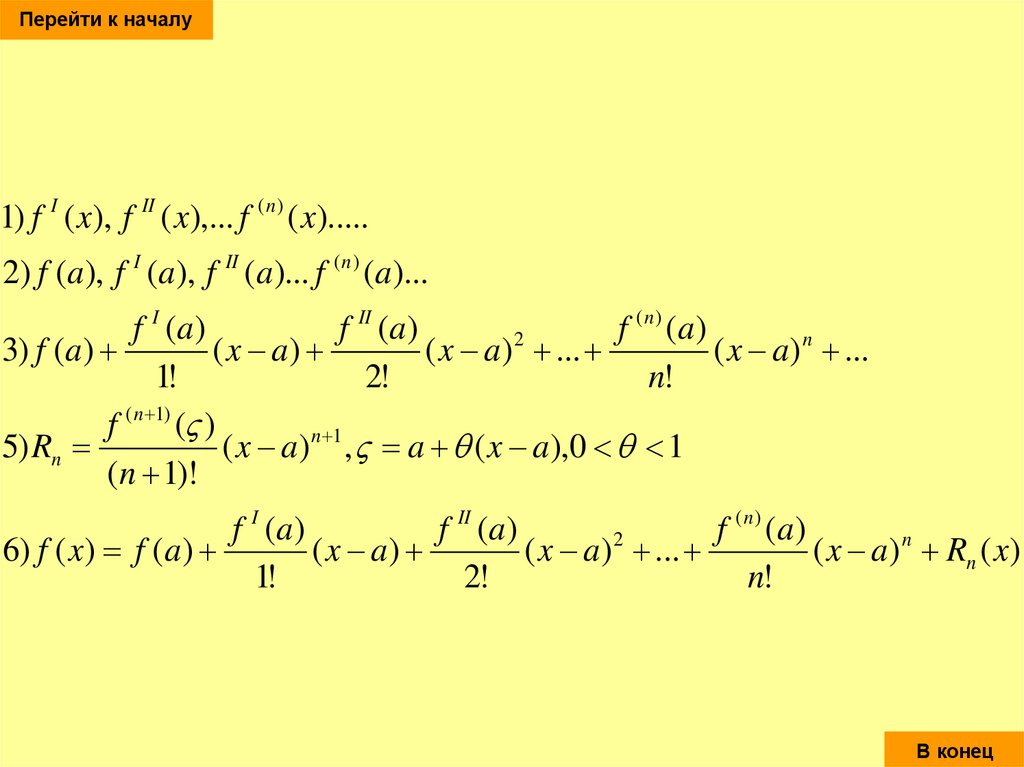





 Математика
Математика








