Кинематика точки. Тема №2

1.

2.

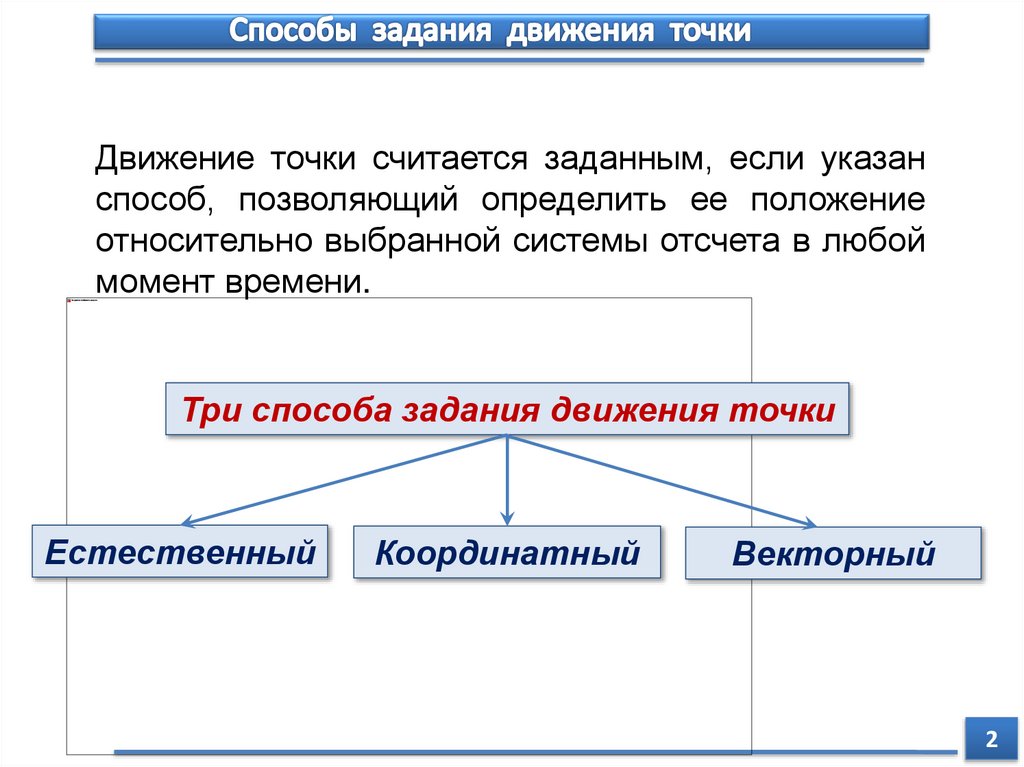
Движение точки считается заданным, если указан
способ, позволяющий определить ее положение
относительно выбранной системы отсчета в любой
момент времени.
Три способа задания движения точки
Естественный
Координатный
Векторный
2

3.

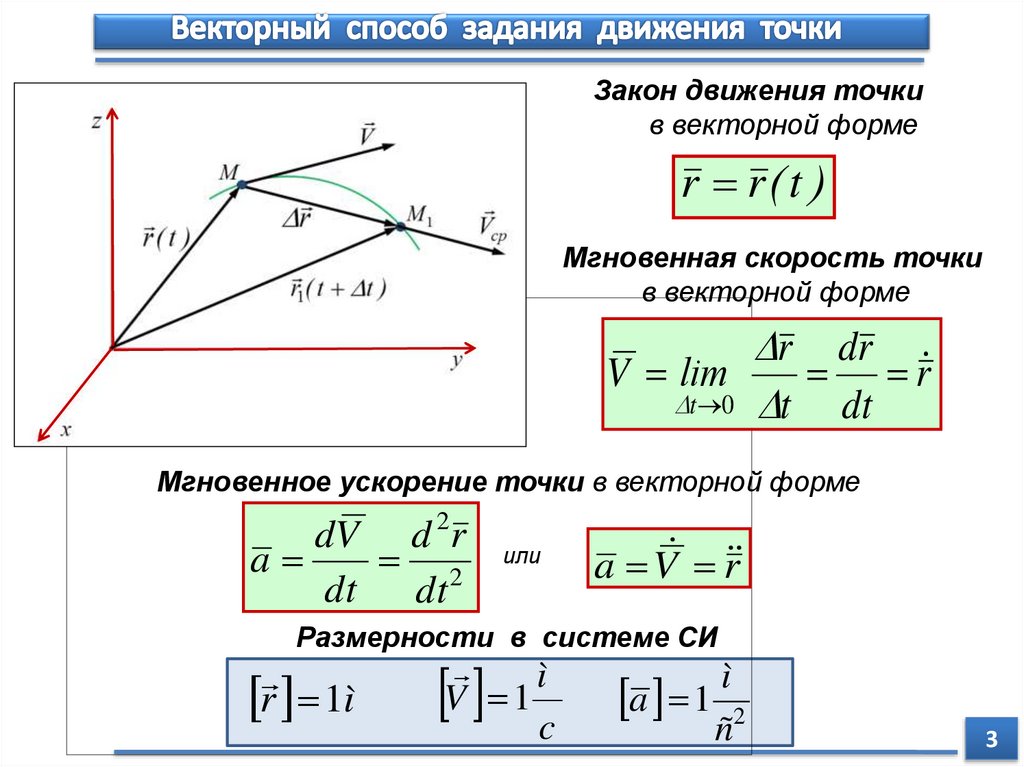
Закон движения точки
в векторной форме
r r( t )
Мгновенная скорость точки
в векторной форме
r dr
V lim
r
t 0 t
dt
Мгновенное ускорение точки в векторной форме
dV d 2r
a
2
dt
dt
или
a V r
Размерности в системе СИ
r 1ì
ì
V 1
c
ì
a 1 2
ñ
3

4.

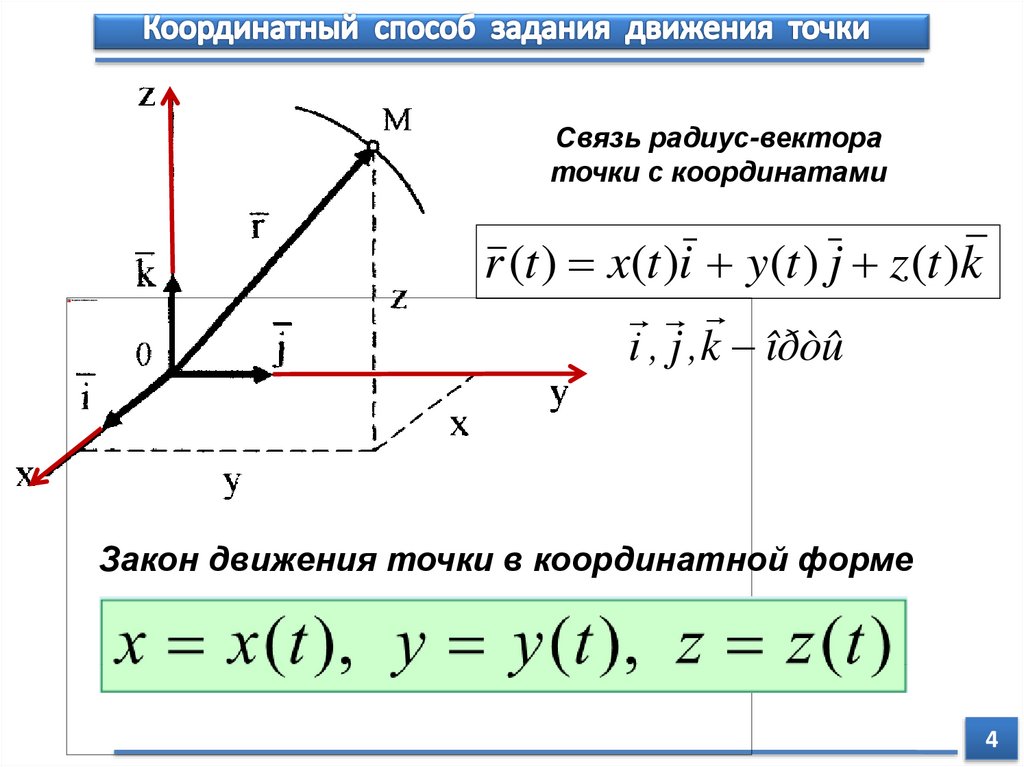
Связь радиус-вектора
точки с координатами
r (t ) x(t )i y(t ) j z (t )k
i , j ,k îðòû
Закон движения точки в координатной форме
4

5.

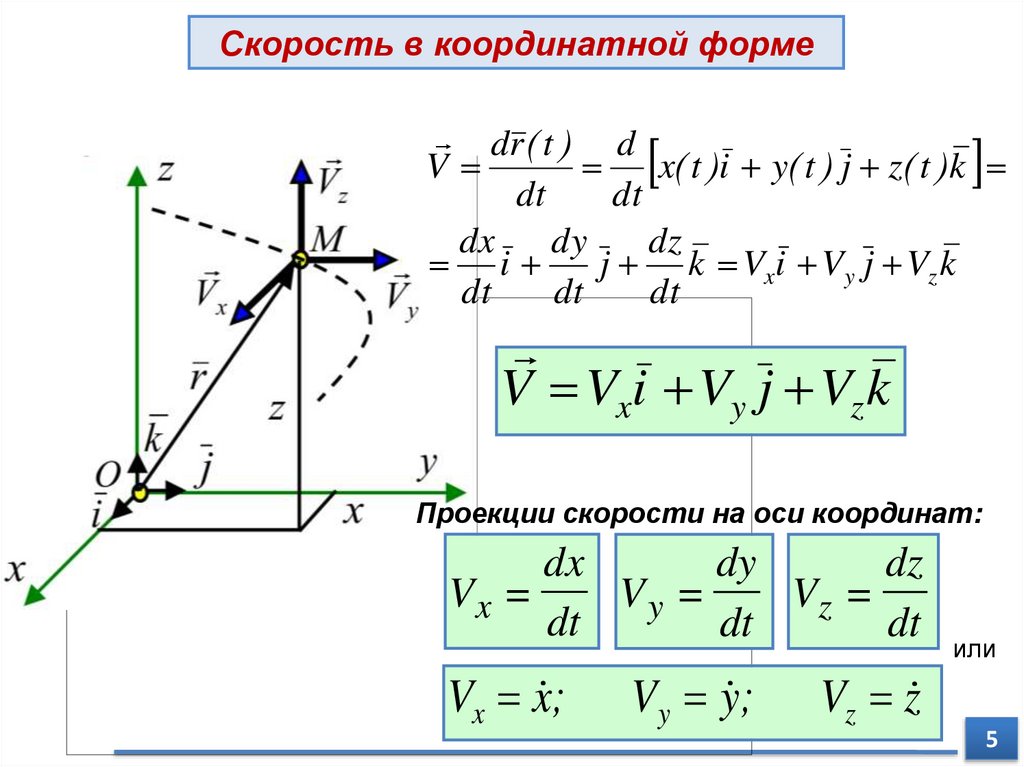
Скорость в координатной форме
dr ( t ) d
V
x( t )i y( t ) j z( t )k
dt
dt
dx
dy
dz
i
j k Vxi Vy j Vz k
dt
dt
dt
V Vxi Vy j Vz k
Проекции скорости на оси координат:
dx
dy
dz
Vx =
Vy =
Vz =
dt
dt
dt
Vx x ;
Vy y ;
Vz z
или
5

6.

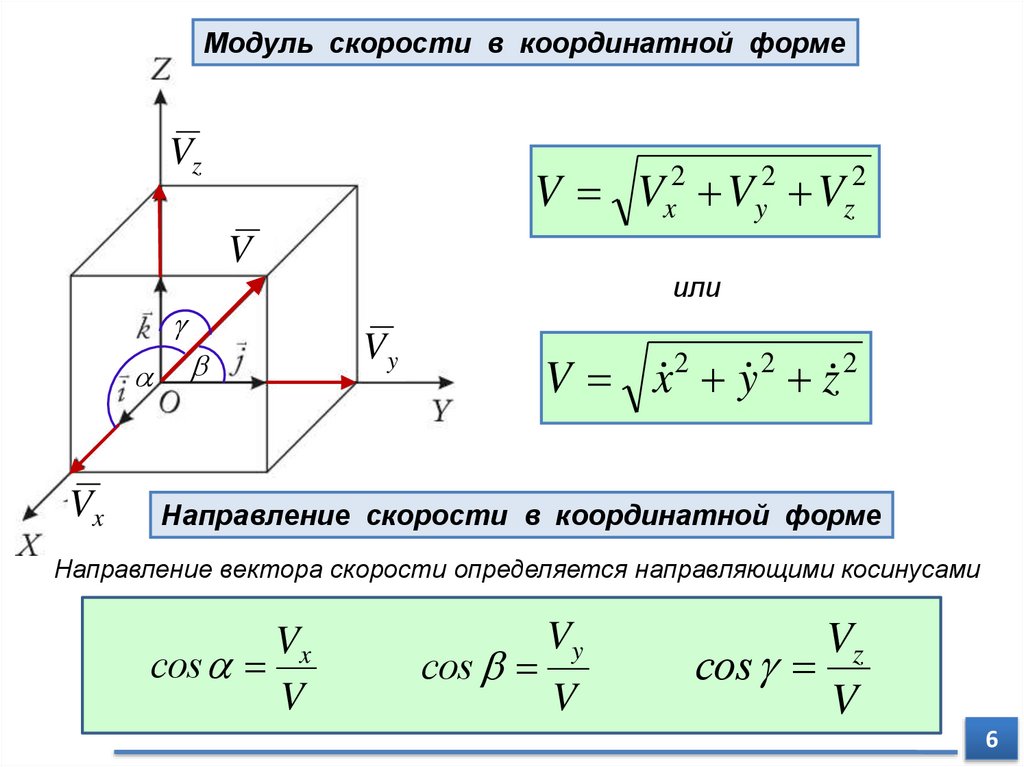
Модуль скорости в координатной форме
Vz
V
V
Vx
2
2
2
Vx Vy Vz
или
Vy
2
2
2
V x y z
Направление скорости в координатной форме
Направление вектора скорости определяется направляющими косинусами
Vx
cos
V
cos
Vy
V
Vz
cos
V
6

7.

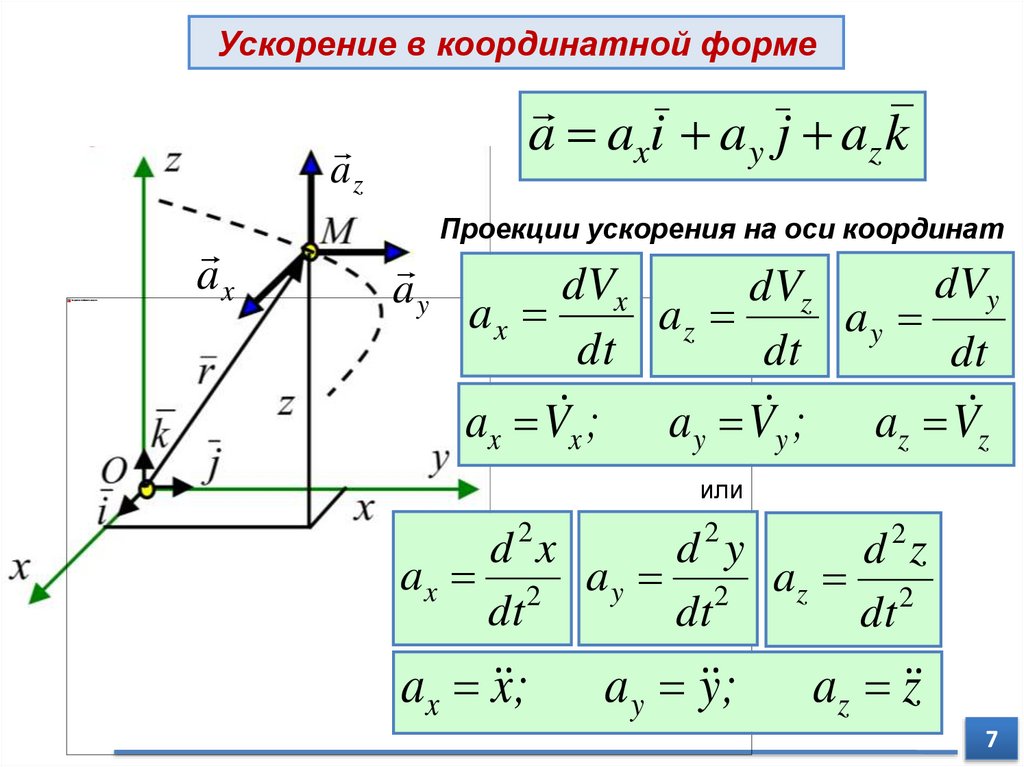
Ускорение в координатной форме
a axi a y j az k
az
ax
ay
Проекции ускорения на оси координат
dVy
dVx
dVz
ax
az
ay
dt
dt
dt
ax V x ; ay V y ; az V z
или
d 2x
d2y
d 2z
ax 2 a y 2 az 2
dt
dt
dt
ax x ;
a y y ;
az z
7

8.

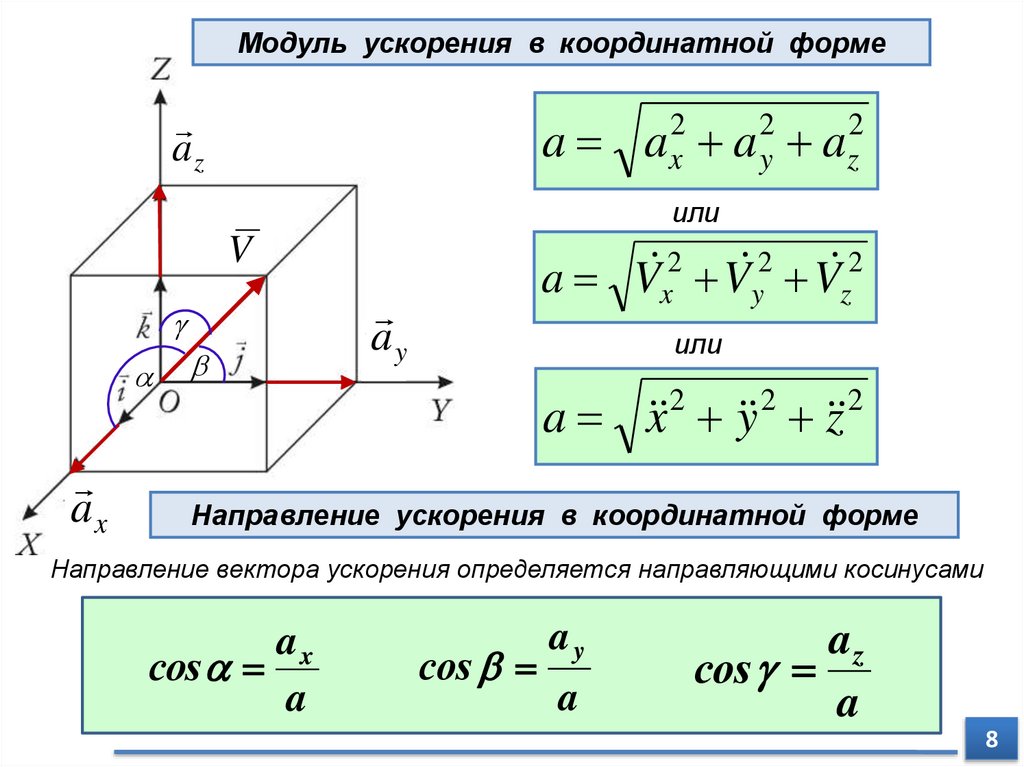
Модуль ускорения в координатной форме
az
V
a
2
2
2
ax a y az
или
V
V
axx
2
2
2
a Vx Vy Vz
Vayy
или
a x 2 y 2 z 2
Направление ускорения в координатной форме
Направление вектора ускорения определяется направляющими косинусами
ax
cos
a
cos
ay
a
az
cos
a
8

9.

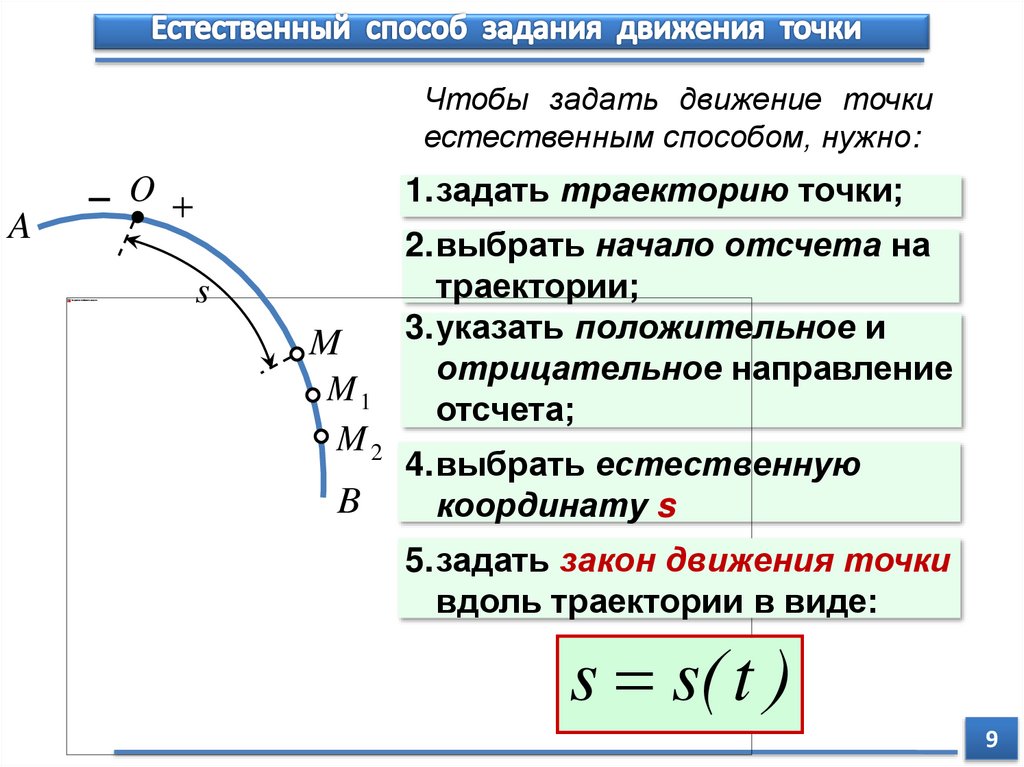
Чтобы задать движение точки
естественным способом, нужно:
A
1.задать траекторию точки;
O
s
M
M1
M2
B
2.выбрать начало отсчета на
траектории;
3.указать положительное и
отрицательное направление
отсчета;
4.выбрать естественную
координату s
5.задать закон движения точки
вдоль траектории в виде:
s s( t )
9

10.

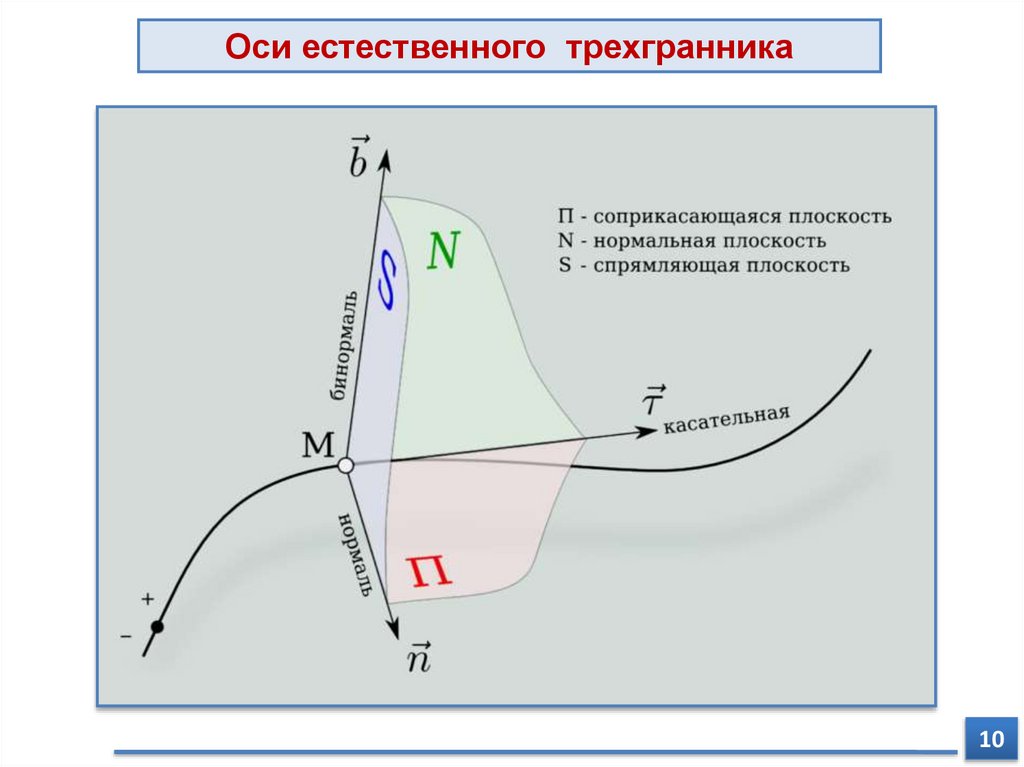
Оси естественного трехгранника
10

11.

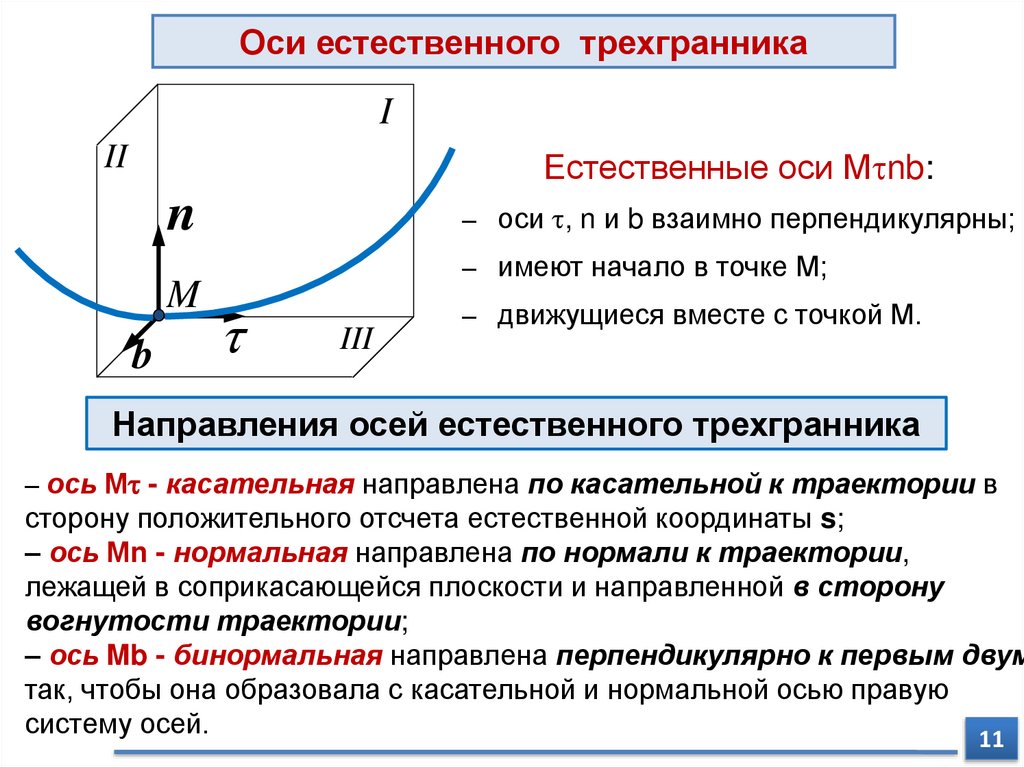
Оси естественного трехгранника
I
II
Естественные оси М nb:
n
M
b
– оси , n и b взаимно перпендикулярны;
– имеют начало в точке М;
III
– движущиеся вместе с точкой М.
Направления осей естественного трехгранника
– ось М - касательная направлена по касательной к траектории в
сторону положительного отсчета естественной координаты s;
– ось Мn - нормальная направлена по нормали к траектории,
лежащей в соприкасающейся плоскости и направленной в сторону
вогнутости траектории;
– ось Mb - бинормальная направлена перпендикулярно к первым двум
так, чтобы она образовала с касательной и нормальной осью правую
систему осей.
11

12.

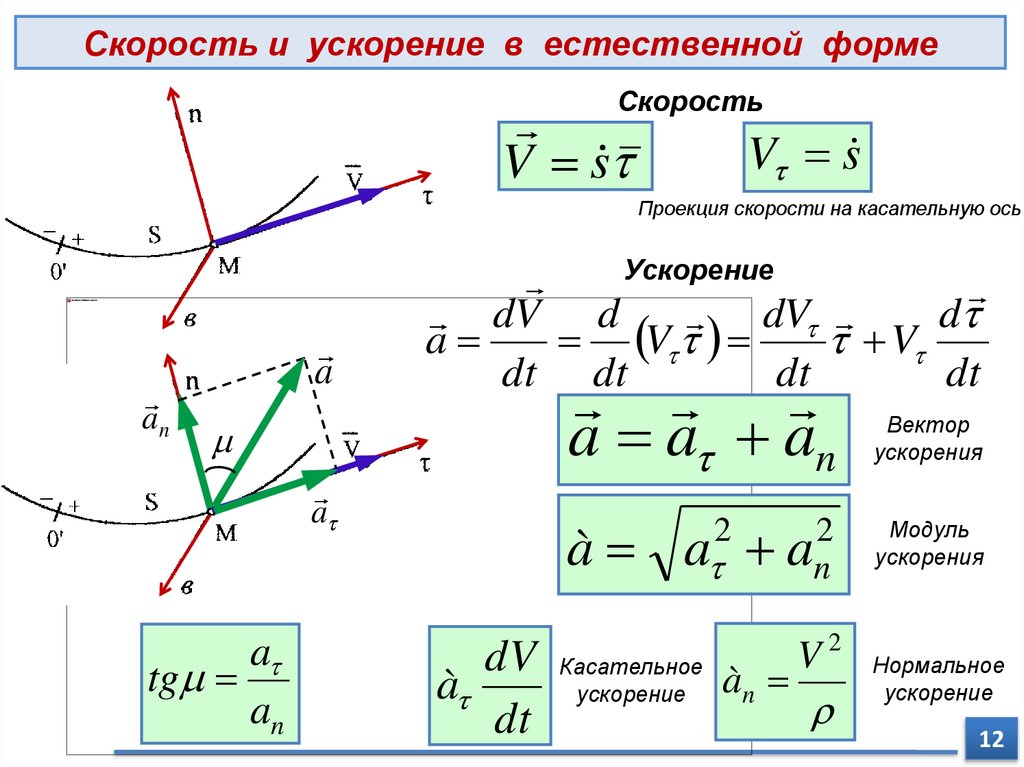
Скорость и ускорение в естественной форме
Скорость
V s
V s
Проекция скорости на касательную ось
an
a
a
a
tg
an
Ускорение
d
dV d
dV
a
V
V
dt dt
dt
dt
a a an
à
2
a an
2
dV Касательное à V 2
à
ускорение
n
dt
Вектор
ускорения
Модуль
ускорения
Нормальное
ускорение
12

13.

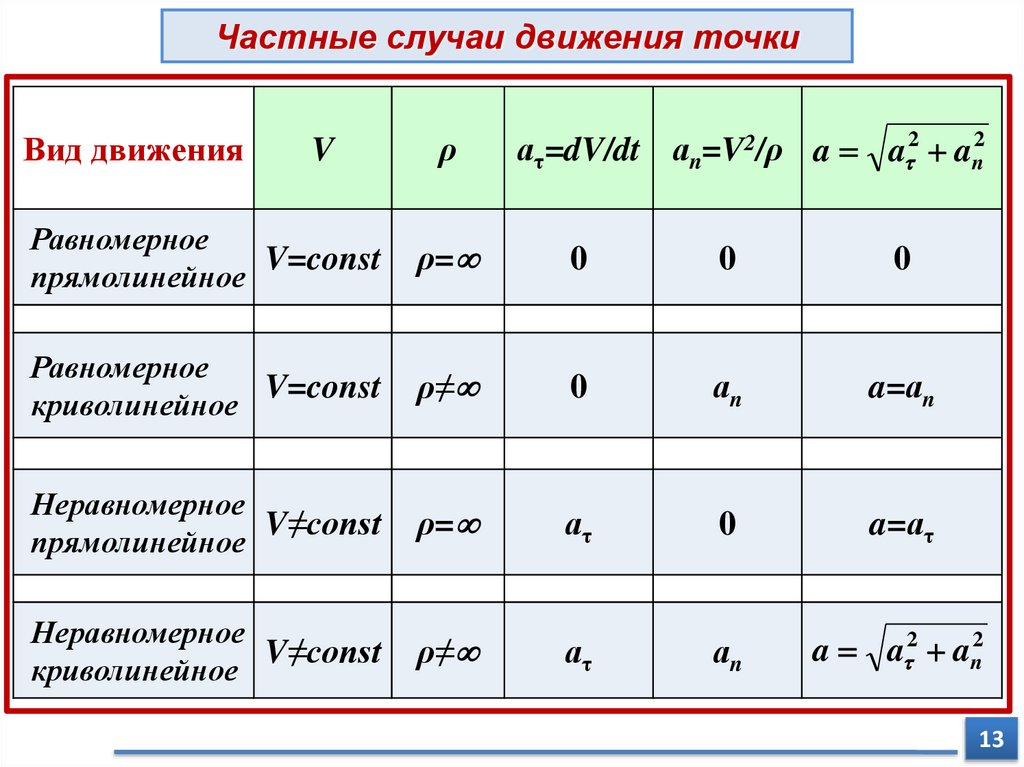
Частные случаи движения точки
Вид движения
V
ρ
аτ=dV/dt аn=V2/ρ a a 2 an2
Равномерное
V=const
прямолинейное
ρ=
0
0
0
Равномерное
V=const
криволинейное
ρ≠
0
аn
a=аn
Неравномерное
V≠const
прямолинейное
ρ=
аτ
0
a=аτ
Неравномерное
V≠const
криволинейное
ρ≠
аτ
аn
a a 2 an2
13

14.

ЛИТЕРАТУРА
1. Яблонский А.А., Никифорова В.М. Курс теоретической
механики – М.: Интеграл-Пресс, 2007. – 608 с.
2. Тарг С.М. Краткий курс теоретической механики. – М.:
Высшая школа, 1986. – 416 с.
3. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической
механики. СПб.: Лань. 2009. – 736 с.
4. Бухгольц Н.Н. Основной курс теоретической механики. В
2-х ч. Ч. 1. Кинематика, статика, динамика материальной
точки. СПб.: Лань, 2009. – 480 с.
5. Диевский В.А. Теоретическая механика – СПб.: Лань,
2005. – 320 с.