Межатомные взаимодействия в конденсированных средах

1. Межатомные взаимодействия в конденсированных средах

2. Уравнения движения классических частиц с потенциальным взаимодействием

U (r1 , r2 ,..., rN )
mi ai Fi
(i 1,2,..., N )
ri
Движение системы классических частиц (материальных точек),
взаимодействие которых характеризуется потенциальной
энергией, описывается системой уравнений II закона Ньютона

3. Классический потенциал и сила взаимодействия

U (r1 , r2 ,..., rN )
Потенциальная энергия системы N атомов
U (r1 , r2 ,..., rN )
Fi
iU (r1 , r2 ,..., rN )
ri
Сила, действующая на i-й атом
Взаимодействие атомов носит квантовый характер и осуществляется
через электроны. Имеет ли обоснование понятие межатомного
потенциала?

4. Но атомы – квантовые объекты !

Строго говоря, взаимодействие атомов носит квантовый характер
и осуществляется через электроны.
Можно ли описывать их взаимодействие классическим
межатомным потенциалом, а движение – классическими
уравнениями движения ?
В этой лекции ниже дается положительный ответ на первую часть
вопроса. Ответ на вторую часть вопроса – в лекции об основах
МД.

5. Уравнение Шредингера для N атомов

( Ri , r )
Ri
r
H ( Ri , r ) E ( Ri , r )
полная волновая функция системы
радиусы-векторы ядер системы
радиусы-векторы электронов
Zi Z j e2
Pˆi2
pˆ 2 1
Zi e2
1
e2
H
i 2M i
2m 2 ij | Ri R j | 2 | r r | i | Ri r |
оператор Гамильтона системы

6. Адиабатическое приближение (Борн, Оппенгеймер, 1923)

me M
( Ri , r ) (r ; Ri ) ( Ri )
(r ; Ri ) - ВФ электронов
( Ri ) - ВФ ядер
Zi Z j e2
Pˆi 2
pˆ 2 1
Zie2
1
e2
i 2 M 2m 2 ij | Ri R j | 2 | r r | i | Ri r
(r ; Ri ) ( Ri )
|
E (r ; Ri ) ( Ri )
Не
содержит
операторов,
воздействующих на координа-ты
ядер Ri
Соответствует взаимодействию ядер
непосредственно через кулоновское
поле и через электронную подсистему

7. Адиабатическое приближение продолжение

2
2
2
Z
Z
e
p
Z
e
1
1
e
H el
i j i
2 ij | Ri R j | 2 | r r | i | Ri r |
2m
2
H el (r ; Ri ) U ( Ri ) (r ; Ri )
2
ˆ
P
i
U ( Ri ) (r ; Ri ) ( Ri ) E (r ; Ri ) ( Ri )
i 2M
H n ( Ri ) E ( Ri )
Pi 2
Hn
U ( Ri )
i 2M i
U ( Ri ) имеет смысл потенциальной энергии системы

8. Парные потенциалы

U (r1 , r2 ,..., rn ) U 1 (ri ) U 2 (ri , r j ) U 3 (ri , r j , rk ) ...
i
i
j i
i
j i k l
U1 – одночастичный член (энергия частиц во внешнем поле или обусловленная
граничными условиями (давлением стенок контейнера))
U2 – двухчастичный (парный) член; взаимодействие каждой пары атомов
определяется только их расстоянием друг от друга и не зависит от присутствия
других атомов
U3 – трехчастичный член, учитывающий влияние третьего атома на
взаимодействие двух атомов
При отсутствии внешнего поля и пренебрежении трех- и многочастичными
взаимодействиями:
1
1
U (r1 , r2 ,..., rn ) (ri , r j ) (ri , r j ) (ri r j )
2 i j 1
2 i j 1
i j i

9. Потенциал Леннарда-Джонса

12 6
(rij ) 4
r
rij
ij
Rmin=1,12
Параметры подгоняются к равновесному
межатомному расстоянию rmin и энергии связи
Потенциал ЛД дает хорошее описание ван-дер-ваальсовских взаимодействий между
атомами инертных газов и молекулами (Ar, Kr, CH4, O2, H2, C2H4 и т.д.). Для Ar: ε=0.0104
эВ, σ=3.40 Å), Ne: ε=0.0031 эВ, σ=2.74 Å, Kr: ε=0.0140 эВ, σ=3.65 Å, Xe: ε=0.020 эВ,
σ=3.98 Å. Для металлов не подходит.
Широко применяется как generic потенциал (отражающий основные черты межатомных
взаимодействий) для качественного изучения явлений в многочастичных системах, в том
числе кристаллических твердых телах (например, общие, качественные, черты
распространения трещины)

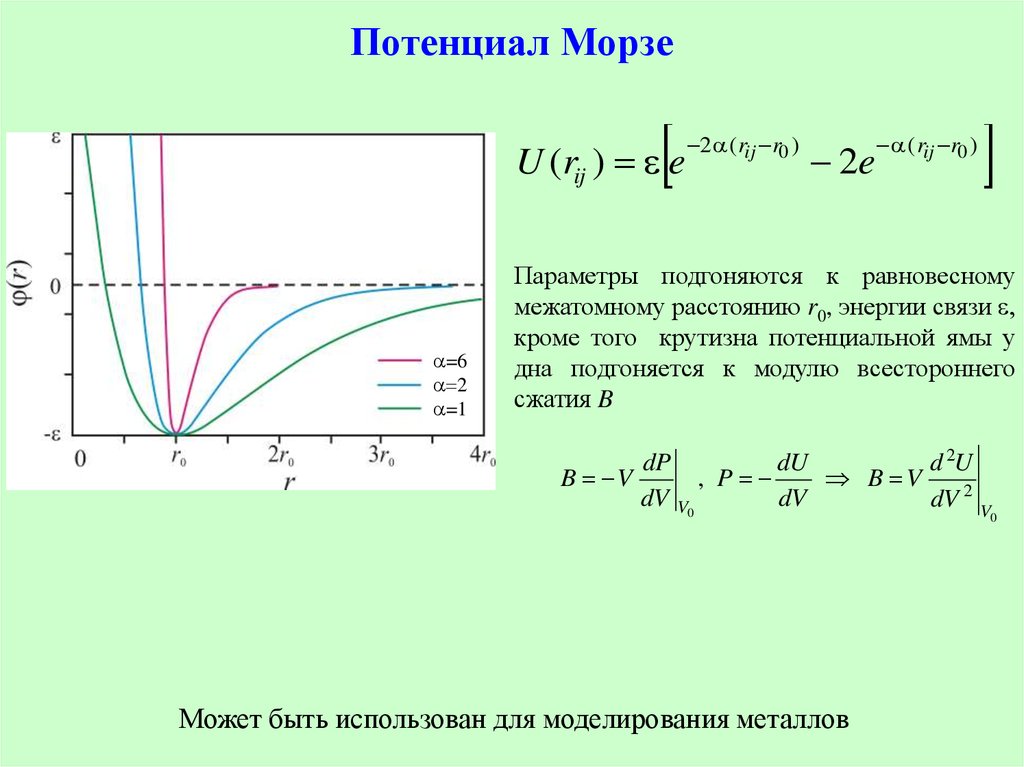
10. Потенциал Морзе

U (rij ) e
=6
2
=1
2 ( rij r0 )
2e
( rij r0 )
Параметры подгоняются к равновесному
межатомному расстоянию r0, энергии связи ,
кроме того крутизна потенциальной ямы у
дна подгоняется к модулю всестороннего
сжатия B
dP
dU
d 2U
B V
, P
B V
dV V0
dV
dV 2
Может быть использован для моделирования металлов
V0

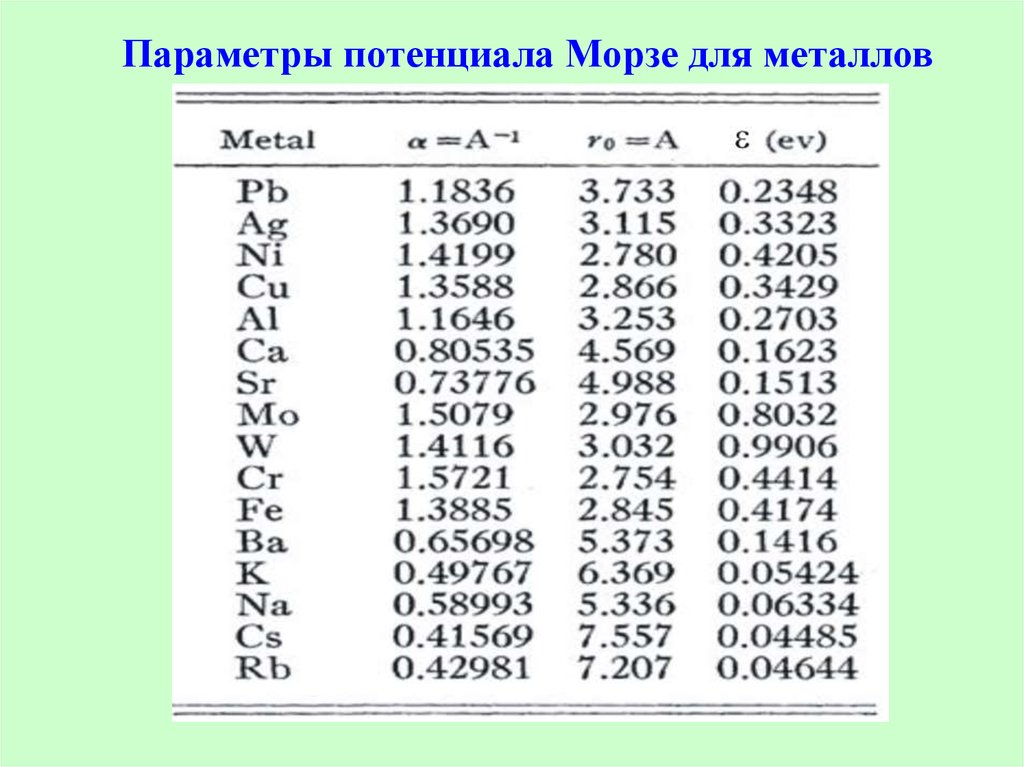
11. Параметры потенциала Морзе для металлов

12. Расчет силы для парных потенциалов

1 N N
Fi iU (r1 , r2 ,..., rN ) (| ri r j
ri
2 i 1 j 1 ( j i )
|) i (| ri r j |)
j i
r
r
r d (| ri r j |)
(| ri r j |) ex ij e y ij ez ij
ex
ey
ez
xi
yi
zi
xi
yi
zi
drij
j i
j i
xij yij zij d (| ri r j |)
ri r j d (| ri r j |)
ex
ey
ez
f ij
rij
rij
rij
drij
rij
drij
j i
j i
j i
Для потенциала ЛД
d (| ri r j |)
drij
6
6
12
6
(ri r j )
1 2
4 12 13 6 7 , Fi 24
8
rij
rij
rij
rij
j i

13. Обрезание потенциалов

U(r)=0 при r>rc
Причины:
1. Число взаимодействующих пар N2
N=3000: N2/2=4 500 000
Радиус обрезания потенциала rc 8-10 Å число соседей 150 000
2. Периодические граничные условия взаимодействие атома
со своим периодическим образом
U (rij ) U (rc ), rij rc
U (rij )
rij rc
0

14. Обрезание потенциалов. Простейший способ

U (rij ) U (rc ), rij rc
U (rij )
rij rc
0
«Приподнять» функцию на величину –U(rс), задав значение радиуса
обрезания rс. При этом функция в точке обрезания будет непрерывной, но ее
производная испытывает скачок, что приводит к скачкообразным изменениям
сил.

15. Обрезание потенциала ЛД без скачка производной

rc

16. Недостатки парных потенциалов

1. Не учитывают насыщение связей: энергия на одну связь в
объеме меньше, чем на поверхности.
2. Не учитывают зависимость силы связи от направления
3. Дают завышенную энергию образования вакансий
против E f (0,25 0,35) св
E f св
4. Неправильно оценивают упругие константы (выполняется
соотношение Коши: c12 c44 ); в действительности:
c12 / c44 1,5 для Cu; 1,9 для Ag и 3,7 для Au

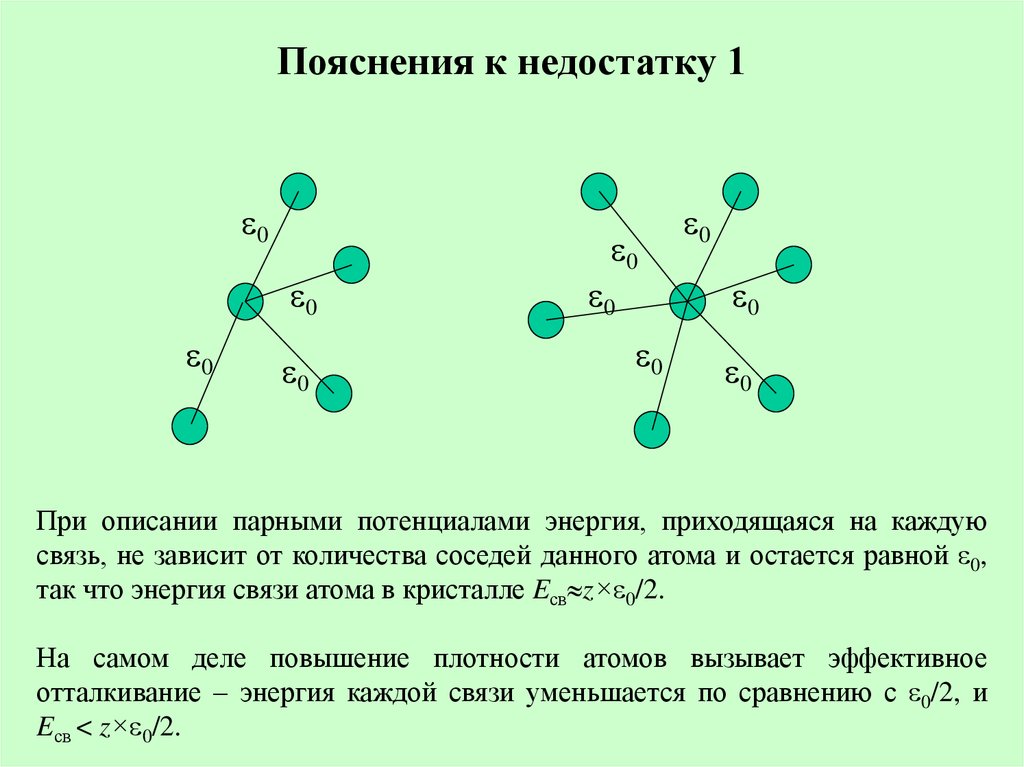
17. Пояснения к недостатку 1

0
0
0
0
0
0
0
0
0
0
При описании парными потенциалами энергия, приходящаяся на каждую
связь, не зависит от количества соседей данного атома и остается равной 0,
так что энергия связи атома в кристалле Eсв z× 0/2.
На самом деле повышение плотности атомов вызывает эффективное
отталкивание – энергия каждой связи уменьшается по сравнению с 0/2, и
Eсв < z× 0/2.

18. Тензор упругих постоянных кристаллов: основные формулы теории упругости

u (r ) r r - поле упругих смещений
1 u u
, - тензор деформации
2 x x
, - тензор напряжений
xx
{ } yx
zz
xy
yy
xy
xz
yz
zz
Обобщенный закон Гука : c
c тензор упругих постоянных, имеет 34 81 компоненту
c c c c
1 1
c - упругая энергия в единице объема
2
2

19. Тензор упругих постоянных кристаллов: независимые постоянные для кубической решетки

Обозначения Фойгта : xx 1, yy 2, zz 3, yz 4, zx 5, xy 6
В кубических кристаллах только три коэффициен та независимы :
c11 с xxxx , c12 с xxyy , c44 с yzyz (или с xyxy )
c11
c12
c
cIJ 012
0
0
c12
c11
c12
0
0
0
c12
c12
c11
0
0
0
0
0
0
c44
0
0
0
0
0
0
c44
0
0
0
0
0
0
c44
Для парных потенциалов :
c12 c44

20. Понятие о теории функционала плотности

Hohenberg P., Kohn W., 1964:
Все аспекты электронной структуры системы взаимодействующих электронов,
находящейся во внешнем потенциальном поле V(r) и невырожденном состоянии,
полностью определяются плотностью электронного заряда (r) (внешнее
потенциальное поле в данном случае означает поле ядер).
Энергия основного состояния взаимодействующего электронного
газа при данном внешнем потенциале является однозначным
функционалом функции (r) , и этот функционал минимизируется
определенной функцией (r).
G[ (r )]
1
E[ ] G[ (r )] V (r ) (r )dr
2
(r ) (r )
dr
| r r |
-функционал кинетической, обменной и корреляционной энергии электронов

21. Энергия связи твердого тела

Z
Z
Z
(
r
) 1
1
i j
i
Eсв G[ ] dr
2 i , j i | Ri R j | i | r Ri |
2
(r1 ) (r2 )
dr1dr2 Eat
| r1 r2 |
суммирование по i и j производится по ядрам твердого тела,
Zi
Ri
- заряд и радиус-вектор i-го ядра,
интегралы берутся по координатам электронов.
Eat - суммарная энергия изолированных атомов

22. Методы описания межатомного взаимодействия, основанные на теории функционала плотности

• Метод погруженного атома (Embedded
atom method, EAM)
• Метод эффективной среды (Effective
medium theory, EMT)
• Потенциал Финниса-Синклера
• Клеевая модель Ерколесси (F. Ercolessi)
• …

23. Метод погруженного атома

N
Etot Ei ,
i 1
1 N
Ei Fi ( i ) ij (rij )
2 j 1
j i
i f j ( Rij ).
j i
i плотность электронов в узле i
Fi
энергия внедрения атома i в эту электронную плотность
ij
энергия парного взаимодействия между атомами i и j
f
электронная плотность, создаваемая одним атомом

24. Составляющие энергии в МПА: схема

25. Парное взаимодействие в МПА

2
1 Z i ( r ) Z j ( r )e
ij (r )
4 0
r
Эффективный заряд атома
Z (r ) Z 0 (1 )r e r
Для атомов разных элементов:
Эффективные заряды для разных металлов;
сплошные линии – Cu, Ag, Au; пунктир –
Ni, Pd, Pt. Заряд в единицах e
A
B
2
Z
(
r
)
Z
(
r
)
e
1
i
j
ijAB (r )
4 0
r
Z0- число внешних электронов (Z0=10, =1 для Ni, Pd, Pt, Z0=11, =2 для Cu,
Ag, Au); =1. Параметры и получаются подгонкой

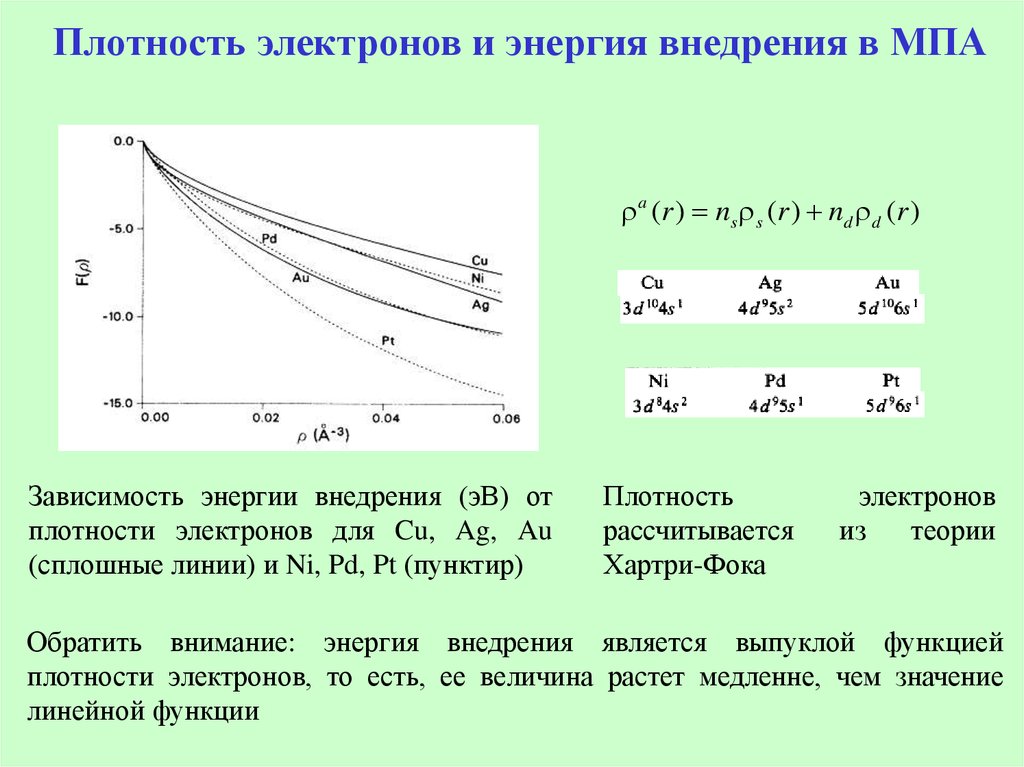
26. Плотность электронов и энергия внедрения в МПА

a (r ) ns s (r ) nd d (r )
Зависимость энергии внедрения (эВ) от
плотности электронов для Cu, Ag, Au
(сплошные линии) и Ni, Pd, Pt (пунктир)
Плотность
рассчитывается
Хартри-Фока
электронов
из
теории
Обратить внимание: энергия внедрения является выпуклой функцией
плотности электронов, то есть, ее величина растет медленне, чем значение
линейной функции

27. Аналитический потенциал МПА Джонсона (1988)

r
f (r ) f e exp 1 ,
re
r rc ;
r
(r ) e exp 1 , r rc
re
F ( ) Eсв 1 ln
e e
3 Va B / Eсв
e 12 f e
B- модуль всестороннего сжатия
/
e
e
/
e 6 e
Va - атомный объем
e , , , rc -параметры, подгоняемые к параметру решетки a или
атомному объему Va, энергии связи Eсв, энергии вакансии Ev,
модулю всестороннего сжатия B и модулю сдвига G

28. Графики функций МПА Джонсона

Энергия внедрения – функция с положительной кривизной
(нелинейная), поэтому взаимодействие становится более
отталкивательным при увеличении плотности

29. Димер и кристалл Ni в МПА

b a / 2 =2,49 Å
b2 2,07 Å

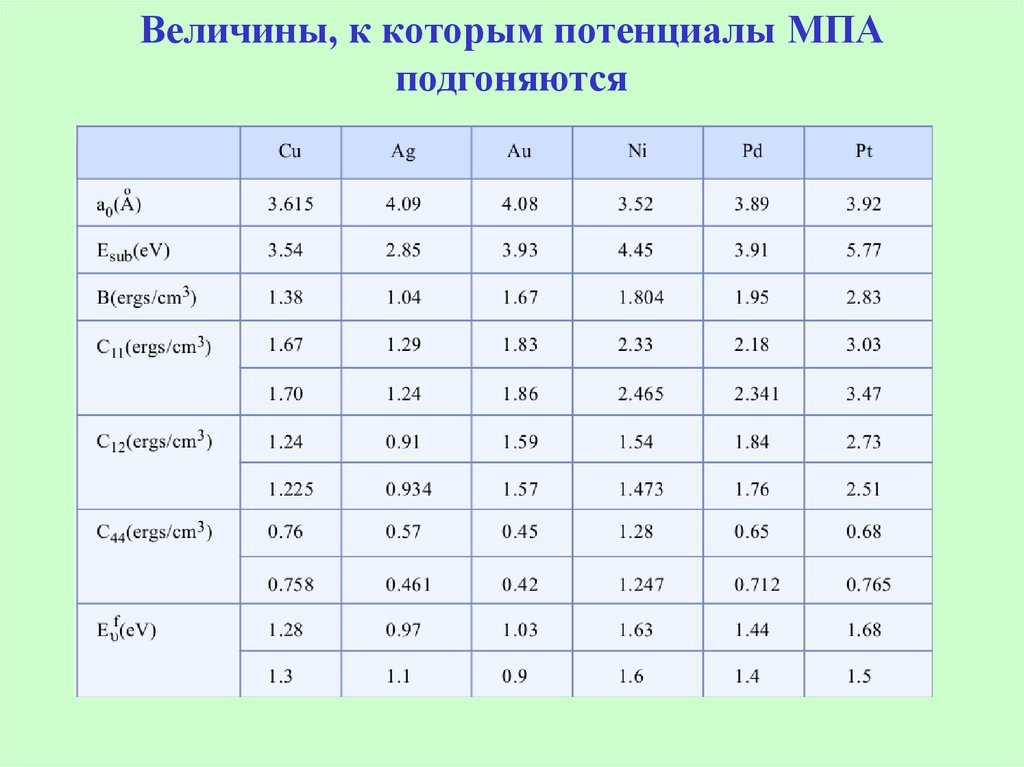
30. Величины, к которым потенциалы МПА подгоняются

31. Результаты расчета физических свойств материалов

Коэффициент термического расширения металлов, 10-6 К-1

32. Результаты расчета физических свойств материалов

Энергия активации самодиффузии в металлах (в эВ)

33. Результаты расчета физических свойств материалов

Рассчитанные энергии низкоиндексных поверхностей металлов
и экспериментальное значение средней энергии поверхности

34. Результаты расчета физических свойств материалов

Температуры плавления металлов, К

35. Таблица потенциала niu3 для никеля

eunit eV
potential set eam 1
potential embed 1
500 0.000000 0.250000
0.0000000000000000E+00 -0.5051701604899677E+00 -0.7931785384826711E+00
...........................................................................
-0.3095312048460391E+02 -0.3102562225632869E+02
potential pair 1 1
499 0.009697 4.838788
0.1454117941298843E+06
0.7133742661881313E+05
0.4665632980925746E+05
...........................................................................
0.0000000000000000E+00
potential dens 1
500 0.000000 4.838788
0.0000000000000000E+00
0.5901012631981482E-04
0.9512300176593089E-03
...........................................................................
0.0000000000000000E+00
0.0000000000000000E+00

36. Потенциал метода МПА для титана

4
Ei F ( i ) (rij )
(r ) ai (ri r ) 3 (ri r )
i 1
j i
i (rij )
j i
При >48
F ( i ) i
При 48 – приближение
кубическим сплайном
8
(r ) ai (ri r ) 3 (ri r )
i 1

37. Таблица потенциала метода МПА для титана

# EAM potential for Ti, T. Hammerschmidt et al. PRB 71, 205409 (2005)
# Tabulated 26 January 2007 by A. Nazarov
# Lattice constants for T=0 K given by XMD: a=2.9664 A, c=4.7226 A, c/a=1.5920
# Reference data: a=2.965 A, c=4.721 A, c/a=1.5920
# Cohesive energy: e0=-4.852832 eV, vacancy formation energy: ef=1.4246 eV
# Reference data: e0=-4.86 eV, vacancy formation energy: ef=1.43 eV
#
eunit eV
potential set eam 1
#
potential pair 1 1 1501
0.500000E+00
0.509113E+01
0.753560E+02
0.750959E+02
0.748364E+02
0.745774E+02
............................................................
-0.144189E-05 -0.608296E-06 -0.180236E-06 -0.225295E-07
0.000000E+00
potential dens 1 1501
0.500000E+00
0.509113E+01
0.246672E+03
0.245784E+03
0.244898E+03
0.244014E+03
............................................................
0.100494E-05
0.423960E-06
0.125618E-06
0.157022E-07
0.000000E+00
potential embed 1 1501
0.000000E+00
0.144000E+03
0.000000E+00 -0.286934E-01 -0.571759E-01 -0.854506E-01
............................................................
-0.119840E+02 -0.119880E+02 -0.119920E+02 -0.119960E+02
-0.120000E+02

38. Потенциал Клери-Росато (приближение второго момента модели сильной связи)

E Ei
i
Ei EiB EiR
EiB
rij
2 q 1
2
r0
e
j
EiR Ae
j
rij
p 1
r0

39. Потенциал Финниса-Синклера

E Ei
i
1
Ei (rij ) A ni
2 j i
ni (rij )
j i

40. Межатомные потенциалы для сплавов. Потенциал Морзе

AA
U KL (r ) KL e 2 RLr 2e KLr
KL =АА, ВВ, АВ
AB
BB
Подгонка характеристик материала:
1)
2)
3)
4)
Параметр решетки,
Энергия связи
Модули упругости,
Теплота смешения сплава

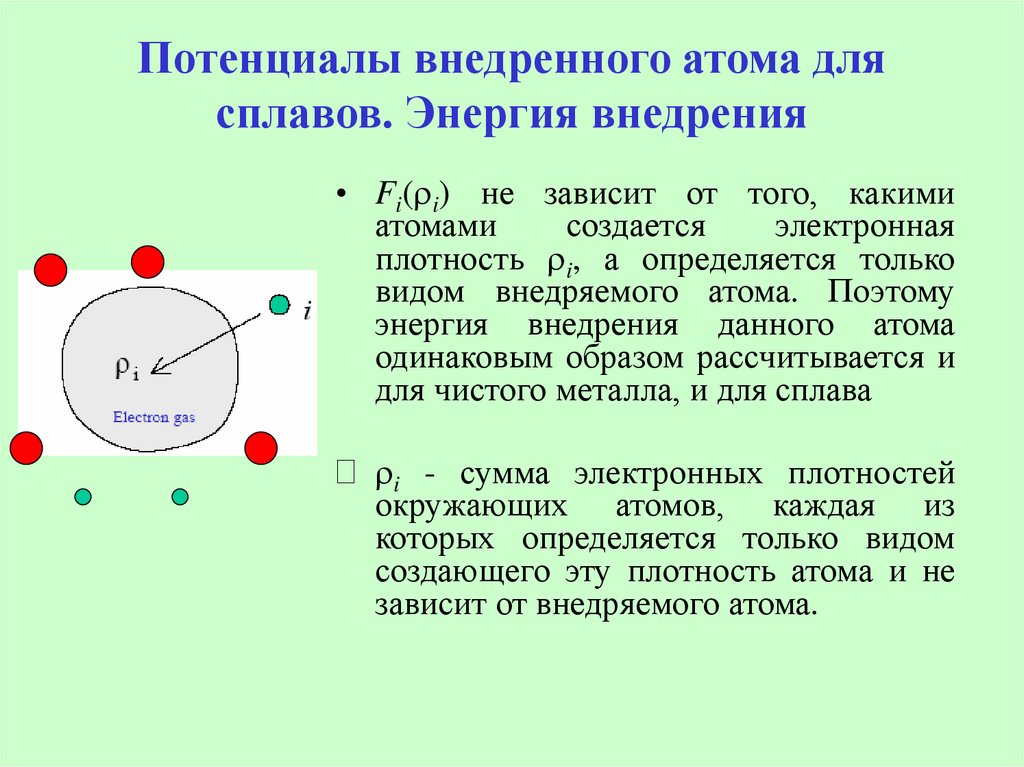
41. Потенциалы внедренного атома для сплавов. Энергия внедрения

• Fi( i) не зависит от того, какими
атомами
создается
электронная
плотность i, а определяется только
видом внедряемого атома. Поэтому
энергия внедрения данного атома
одинаковым образом рассчитывается и
для чистого металла, и для сплава
i - сумма электронных плотностей
окружающих атомов, каждая из
которых определяется только видом
создающего эту плотность атома и не
зависит от внедряемого атома.

42. Потенциалы внедренного атома для сплавов. Энергия парного взаимодействия

Z A (r ) Z B (r )
AB (r )
r
Z A (r ) Z B (r )
- эффективные заряды атомов А и В
Z (r ) Z 0 (1 r )e
r
• Z0, , , подгоночные параметры

43. Функции, необходимые для двухкомпонентного сплава

f B (r )
• Электронные
плотности,
создаваемые атомами А и В
FA ( ) FB ( )
• Энергии внедрения атомов А и В в
электронную плотность
Z A (r ) Z B (r )
f A (r )
Эффективные заряды атомов А и В

44. Потенциалы для ковалентных материалов

• C
• Ge
• Si
(He)2(2s)2(2p)2
(Ne)10(3s)2(3p)2
(Ar)18(4s)2(4p)2
109,5

45. Потенциал Стиллингера-Вебера

U (r1 , r2 ,..., rN ) U 2 (ri , r j ) U 3 (ri , r j , rk ) ...
i
j i
i
p
ij
U 2 (rij ) A( Br
j i k j
c
r ) exp
rij rc
k
U 3 (rij , rik , rjk ) h(rij , rik , jik ) h(rji , rjk , ijk ) h(rki , rkj , ikj )
2
h(rij , rik , jik ) exp
cos jik
rij rc rik rc
cos109,47 1 / 3 :
j
ijk
q
ij
зависящий от угла член проводит к энергетически
выгодной кристаллической структуре алмаза с
тетраэдрическими углами для Si
i

46. Недостатки потенциала Стиллингера-Вебера и другие потенциалы

Недостатки потенциала СтиллингераВебера и другие потенциалы
• Трехчастичный член определяет только одну равновесную
конфигурацию 109.47 , поэтому его трудно распространить на
углерод, для которого существует множество равновесных углов:
180 , 120 и 109.47 , благодаря чему углерод имеет множество
модификаций, как графит, алмаз, фуллерены, нанотрубки и т.д.
• Слишком жесткая установка тетраэдрического расположения связей
приводит к неправильному описанию релаксации на поверхности и
около дефектов, где координация нарушена
• Для элементов IV группы были разработаны потенциалы кратной
связи (bond order potentials), основанные на учете зависимости
прочности связи от локального окружения (потенциалы ТерсоффаАбеля для Si и Ge, потенциал Бреннера для C). Эти потенциалы
являются в настоящее время наиболее употребительными при
моделировании ковалентных кристаллов

47. Использование табулированных межатомных потенциалов

Значения всех функций, определяющих потенциальную энергию, в конечном
числе равномерно расположенных точек записываются в таблицу потенциалов – в
отдельный файл. Для любого значения аргумента в интервале между двумя
соседними точками, в которых значения потенциала заданы таблично,
неизвестное значение потенциала определяется интерполяцией