Похожие презентации:
Сложное движение точки и твердого тела
1.
Дудко Ольга Николаевна, Лидскийколледж УО ГрГУ им.Я.Купалы
2.
Перечень вопросов:1. Плоскопараллельное движение. Скорость
и ускорение.
2.Мгновенный центр скоростей.
3.Сложное движение точки.
Дудко Ольга Николаевна
2
3.
Дудко Ольга Николаевна3
4.
1. Плоскопараллельное движениетвердого тела (плоское)
Плоскопараллельным (плоским) движением
твердого тела называется такое движение, при
котором все точки тела движутся в плоскостях,
параллельных одной неподвижной плоскости,
которая называется основной плоскостью.
Дудко Ольга Николаевна
4
5.
ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕz
Рассмотрим произвольное сечение.
Произвольные точки сечения А и B
спроецируем на основную плоскость.
A
B
Прямые АА1, ВВ1,
параллельны , следовательно
движение этих прямых
поступательное
C
D
y
В1
x
А1
Основная плоскость
Вывод: Для исследования
плоскопараллельного движения
тела достаточно изучить
движение одной плоскости
этого тела параллельной
основной.
Дудко Ольга Николаевна
5
6.
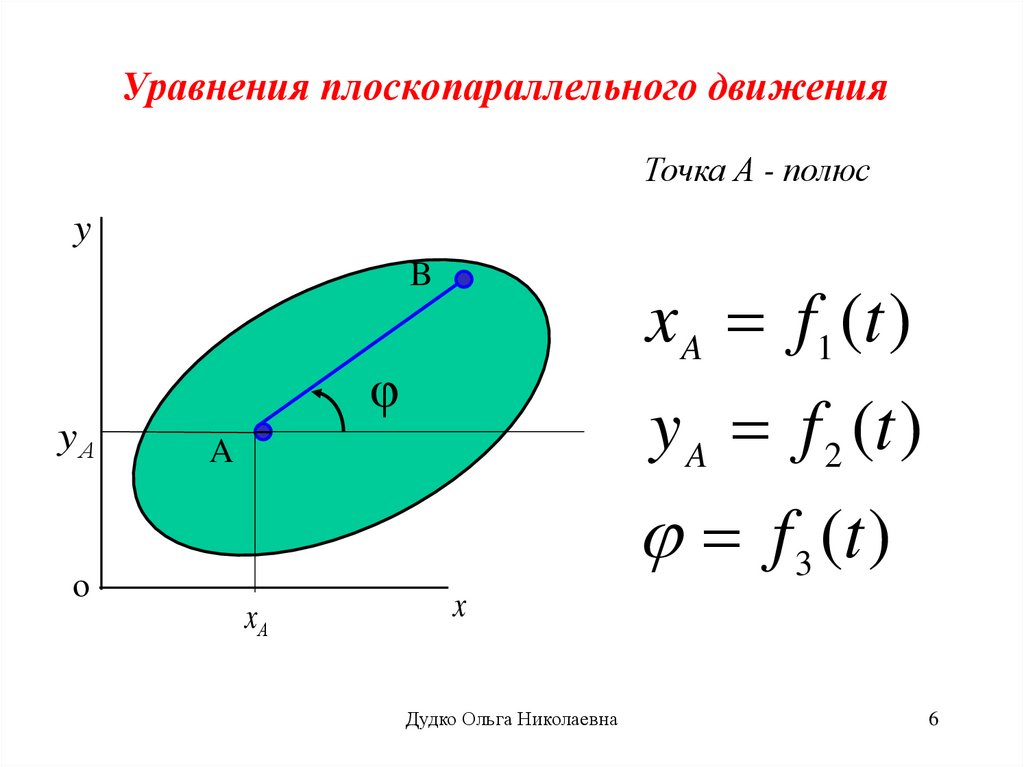
Уравнения плоскопараллельного движенияТочка А - полюс
y
B
x A f1 (t )
φ
yА
y A f 2 (t )
A
f 3 (t )
o
xА
x
Дудко Ольга Николаевна
6
7.
Пример плоскопараллельного движения твердоготела
z
y
O
c
x
Vc
8.
Разложение плоскопараллельного движения напростейшие виды движения
Плоскопараллельное движение можно разложить на поступательное
движение вместе с полюсом и вращательное вокруг оси,
проходящей через полюс.
Было АВ
Стало А1В1
y
А
k
z
Угол φ не зависит
от выбора полюса
В
А2
В1
φ
А1
x
k
Дудко Ольга Николаевна
φ
В2
k
8
9.
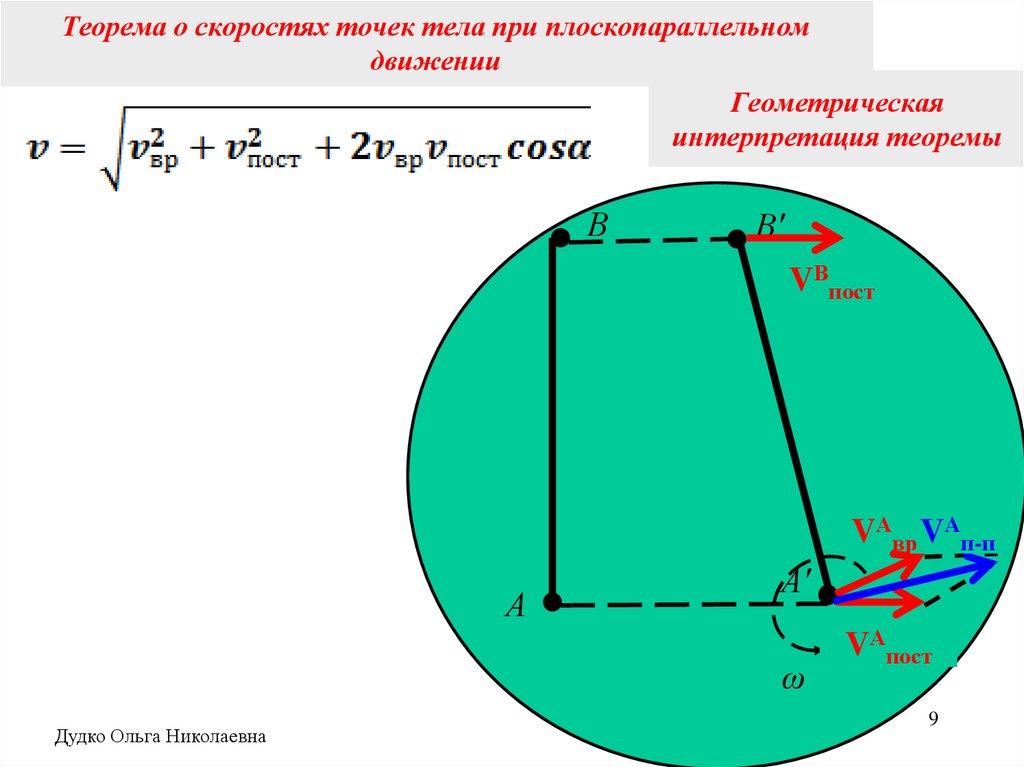
Теорема о скоростях точек тела при плоскопараллельномдвижении
Геометрическая
интерпретация теоремы
В
В′
VВпост
VАвр VАп-п
А
А′
ω
Дудко Ольга Николаевна
VАпост
9
10.
Теорема о сложении ускорений точек приплоскопараллельном движении тела
A
ап-п
авр
аn
В
Ускорение произвольной точки тела при
плоско- параллельном движении состоит из
двух частей: поступательного и
вращательного.
Но так как вращательное ускорение
раскладывается на две составляющие:
центростремительную и касательную, то
вектор ускорения можно представить так:
aB a пост a a пост an at
вр
аt
В
апост
Дудко Ольга Николаевна
10
11.
.Пример: материальная точка совершает плоскопараллельное движение.
Сначала движется поступательно по закону S=3t2+2t+4 в течение 3
секунд, а затем поворачивается на угол φ=2t2-4t+5 на протяжении 2
секунд. Определить v и а точки, если известно, что R=2м.
1.Найдем поступательную
движении.
составляющую
скорости
при
плоскопараллельном
2.Найдем вращательную составляющую скорости
3.Найдем полную скорость при плоскопараллельном движении.
Угол φ=2·22-4·2+5=5рад=5·57=285˚ cos285=0.8
4.Найдем поступательную составляющую ускорения
движении.
Дудко Ольга Николаевна
при плоскопараллельном
11
12.
Пример: материальная точка совершает плоскопараллельное движение.Сначала движется поступательно по закону S=3t2+2t+4 в течение 3
секунд, а затем поворачивается на угол φ=2t2-4t+5 на протяжении 2
секунд. Определить v и а точки, если известно, что R=2м.
5.Найдем вращательную составляющую ускорения. Для этого сначала необходимо
найти угловое ускорение.
6.Найдем полное ускорение точки при плоскопараллельном движении
Ответ:
v=26,8 м/с
а=37,8 м/с2
Дудко Ольга Николаевна
12
13.
Дудко Ольга Николаевна13
14.
VAМгновенный центр
скоростей
B
A
VB
P
Выберем точку P за полюс
Мгновенным центром скоростей
(МЦС) называется точка связанная
с телом, скорость которой в
данный момент времени равна
нулю.
Точка P – мгновенный центр
скоростей. VP=0
VA VP VAP
VAP AP
VB VP VBP
VBP BP
Точка P находится на пересечении перпендикуляров,
восстановленных к скоростям в точках «А» и «В»
Дудко Ольга Николаевна
14
15.
Соотношения между скоростями точек тела иугловой скоростью
VA
VA VB VC
AP BP CP
B
A
VB
С
P
VС
Скорости точек прямо пропорциональны
расстояниям от точек до МЦС
Угловая скорость тела равна отношению
скорости любой точки тела на расстояние
от этой точки до МЦС.
Вывод
Плоскопараллельное движение можно рассматривать
как мгновенное вращение вокруг мгновенной оси
(ось, проходящая через МЦС).
15
Дудко Ольга Николаевна
16.
Скорости двух точек тела параллельны другдругу, не равны между собой и перпендикулярны
прямой соединяющей эти точки.
А
VA
А
VA
Р
В
VB
В
VB
Р
16
Дудко Ольга Николаевна
17.
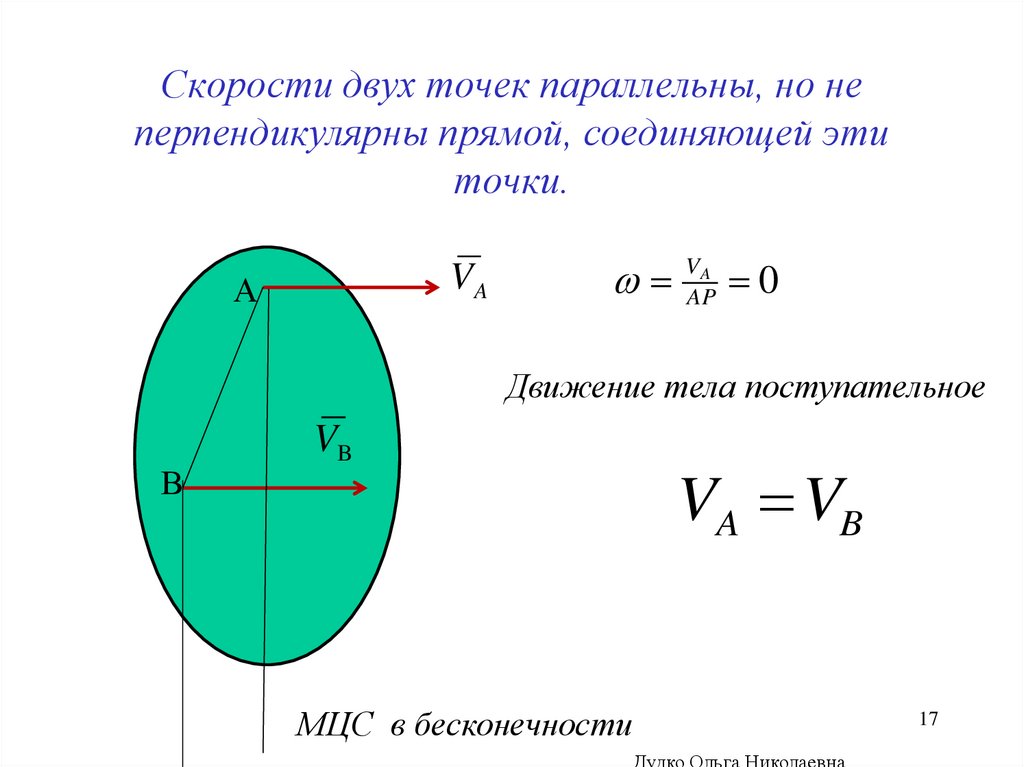
Скорости двух точек параллельны, но неперпендикулярны прямой, соединяющей эти
точки.
VA
А
VA
AP
0
Движение тела поступательное
В
VB
VA VB
МЦС в бесконечности
17
Дудко Ольга Николаевна
18.
4. Тело катится без скольжения по неподвижнойповерхности.
VA
А
VС
С
ω
P МЦС
Дудко Ольга Николаевна
Vp 0
18
19.
Пример 1VA
A
P
ωAB
VС
C
O
VB
ωOA
B
ωAB = 0
A
C
(.) P в ∞
ωOA
!! мгн.поступат.движ. O
VB
VС
VA
ωOA
A
O
VA
C
VС
Дудко Ольга Николаевна
B
B
VB
ωAB (.)P в (.)В
19
20.
Дудко Ольга Николаевна20
21.
Сложное движение точкиСложное движение точки
Сложное движение точки - такое движение,
которое может быть составлено из двух
(нескольких) простых.
Движение рассматривается в двух системах
отсчета: основной (неподвижной) и движущейся.
22.
Сложное движение точким
z
z'
r
o'
x'
o
x
y'
y
23.
Примеры: движение человека по вагонудвижущегося поезда, движение человека по салону
движущегося автобуса, движение человека в лодке,
которая движется по течению реки и т.д.
23
24.
Сложное движение точкиПри сложном движении различают три вида
движения:
1.Переносное – это движение подвижной
системы координат относительно неподвижной.
2.Относительное – это движение материальной
точки М в подвижной системе относительно
неподвижной.
3.Абсолютное – это движение материальной
точки М в подвижной системе координат
относительно неподвижной системы координат.
25.
Дудко Ольга Николаевна25
26.
Сложное движение точкиАбсолютная
относительно
скорость точки - скорость
неподвижной системы отсчета.
Относительная скорость точки - скорость
относительно
подвижной
системы
отсчета
Скорость неизменно связанной с подвижными
осями точки, с которой в данный момент совпадает
движущаяся точка, называется переносной
скоростью.
27.
Сложное движение точкиТеорема о сложении скоростей:
V Vотн Vпер
Абсолютная скорость точки равна геометрической
сумме переносной и относительной скоростей
28.
Сложное движение точкиСкорости и ускорения при сложном движении
обозначаются
Va ,
aa - абсолютные
Vr ,
ar - относительные
Ve ,
ae - переносные
Сложение векторов скорости по теореме косинусов
Va
Ve
Vr
Va Vr Ve
Va Vr2 Ve2 2VrVe cos
29.
Сложное движение точкиТеорема Кориолиса
a aотн апер аКор
Абсолютное
ускорение
точки
равно
геометрической сумме переносного ускорения,
относительного ускорения и ускорения Кориолиса
30.
Домашнее задание:Дудко Ольга Николаевна
30
31.
Дудко Ольга Николаевна31




























 Физика
Физика








