Похожие презентации:
Тренажер по тригонометрии
1. Тренажер по тригонометрии
МБОУ Якшур-Бодьинская гимназияТренажер по тригонометрии
Автор: учитель математики
Малых Ольга Александровна
2. Аннотация
Для успешного решения тригонометрических уравненийи неравенств нужно усвоить формулы приведения,
знать определение обратных функций и их свойства,
определять
знаки
тригонометрических
функций,
работать с единичной окружностью.
Данный тренажер поможет вам в этом.
Перейти
к оглавлению
Выход
3. Выбери тренажер
• Нахождение числа соответствующей точке наединичной окружности
• Нахождение на единичной окружности точки с
заданными координатами
• Определение знаков тригонометрических функций
• Таблица значений arcsinα, arccosα
• Обратные тригонометрические функции
• Математическое лото по решению простейших
тригонометрических уравнений
• Тест по простейшим тригонометрическим уравнениям
4. Нахождение числа по соответствующей точке на единичной окружности
ПравилаСделайте
клик
мышью
по
числу,
соответствующему выделенной точке на
числовом круге.
Для перехода на следующий слайд щелкните
по ссылке «Далее», которая появляется в
случае верно выполненного задания
НАЧАТЬ
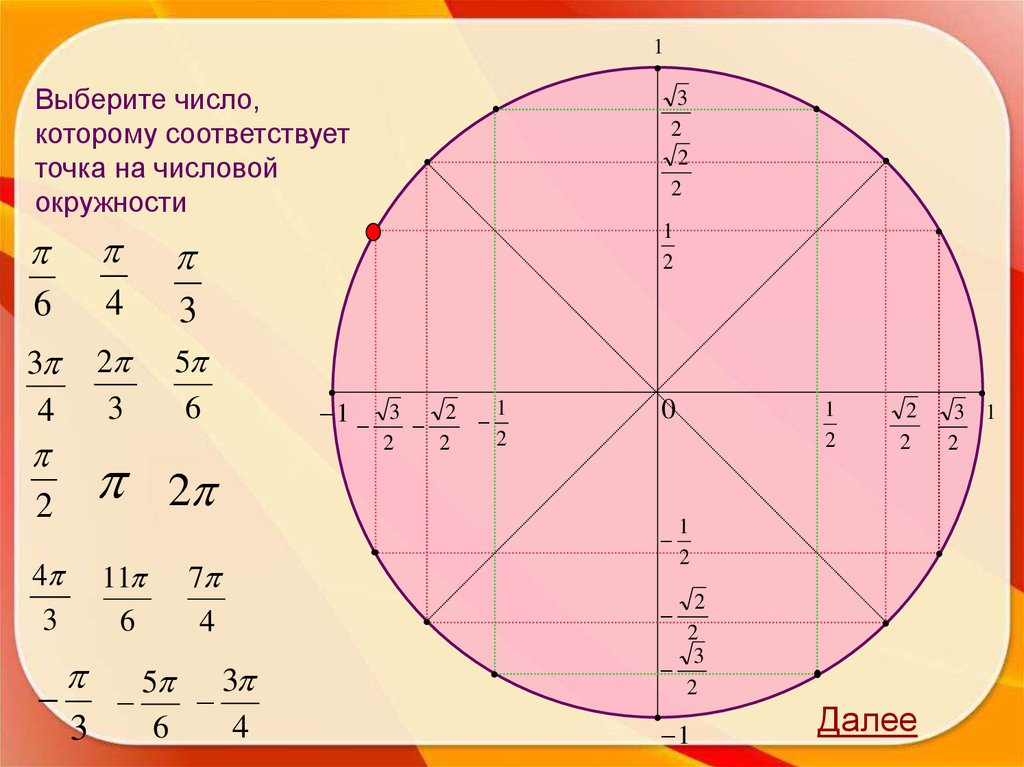
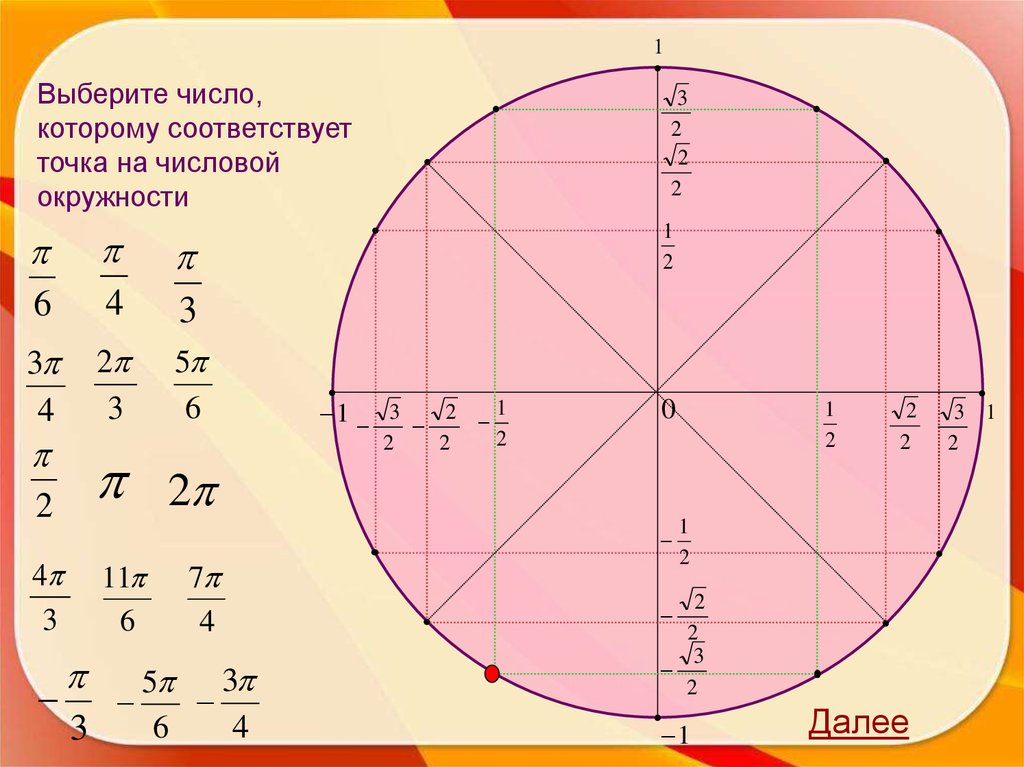
5.
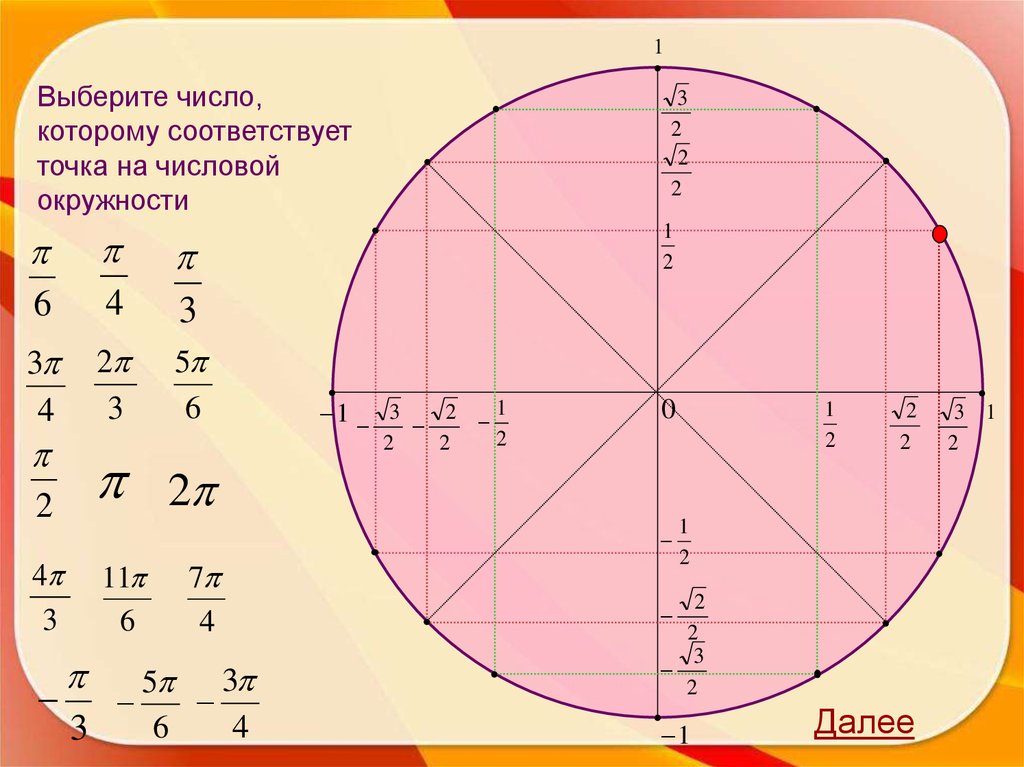
1Выберите число,
которому соответствует
точка на числовой
окружности
6
4
3
3
4
2
3
5
6
2
2
3
2
2
2
1
2
1 3 2 1
2
2
0
2
4
3
11
6
7
4
5 3
6
4
3
1
2
2
2
1
2
2
2
3
2
1
Далее
3 1
2
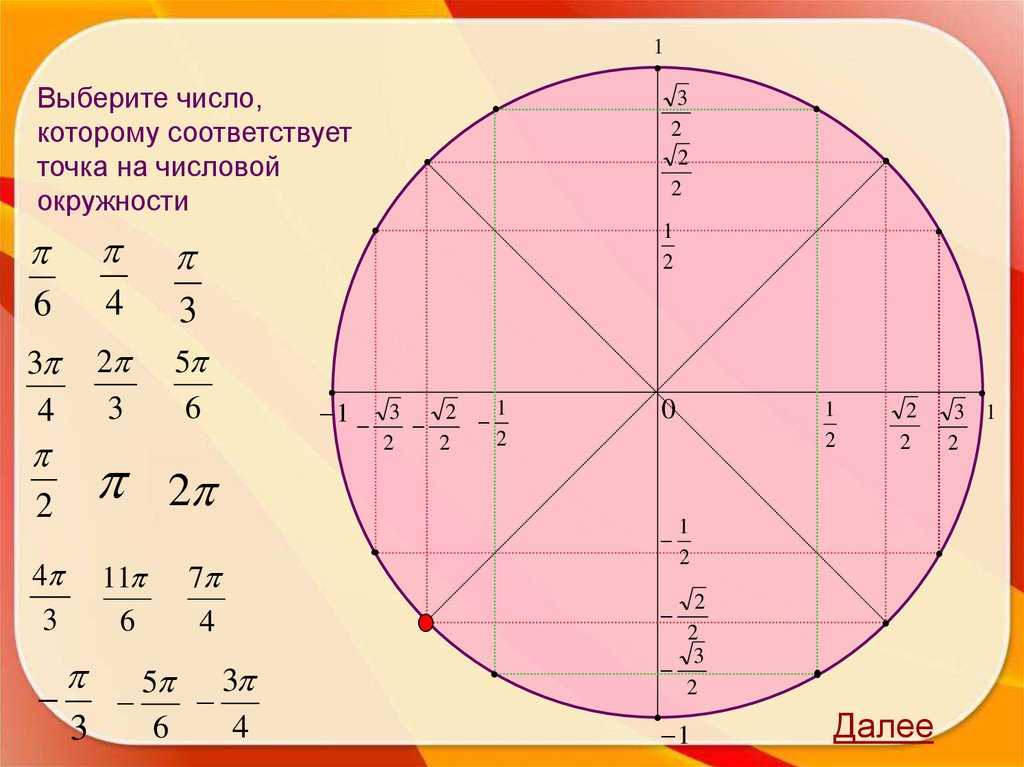
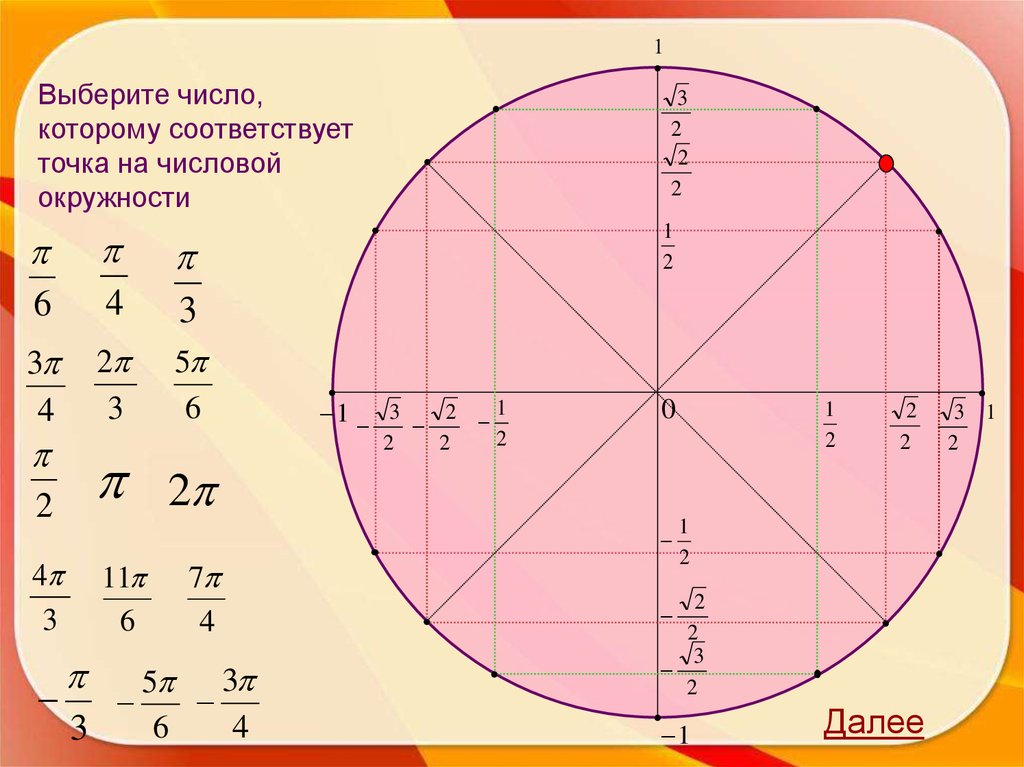
6.
1Выберите число,
которому соответствует
точка на числовой
окружности
6
4
3
3
4
2
3
5
6
2
2
3
2
2
2
1
2
1 3 2 1
2
2
0
2
4
3
11
6
7
4
5 3
6
4
3
1
2
2
2
1
2
2
2
3
2
1
Далее
3 1
2
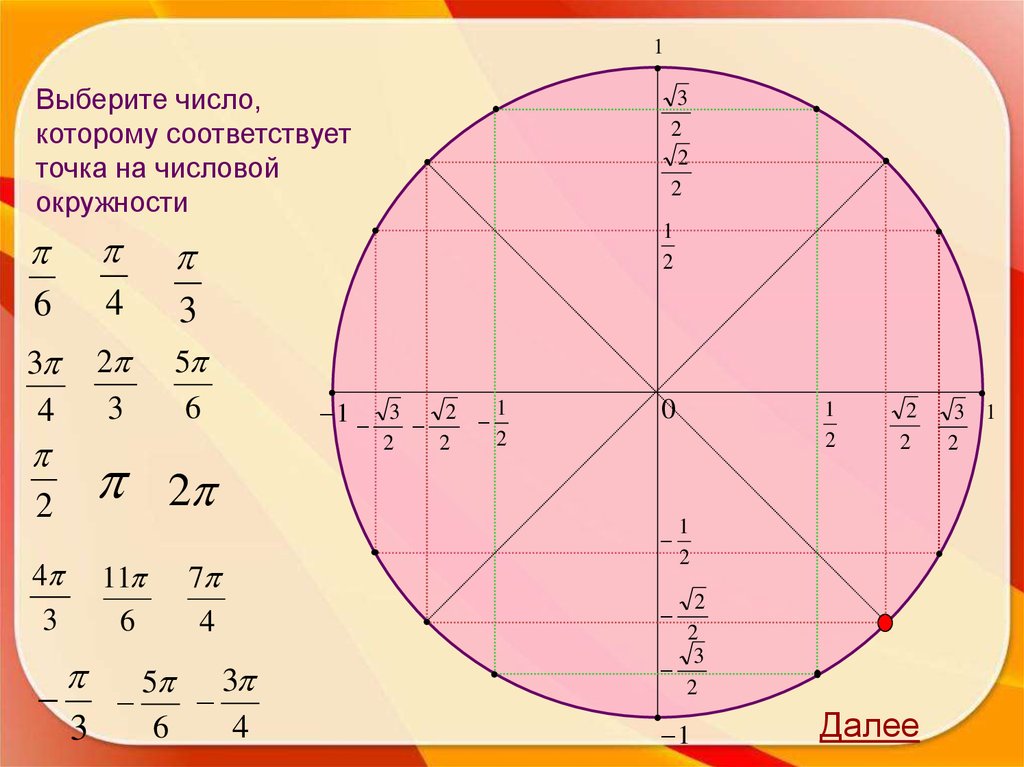
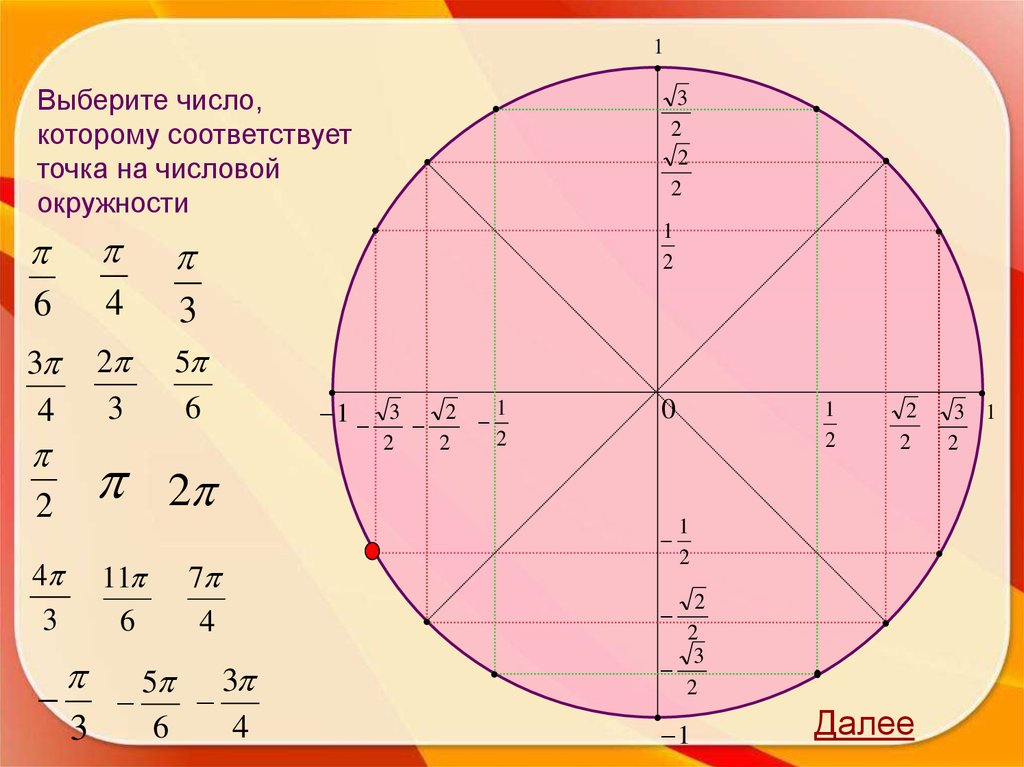
7.
1Выберите число,
которому соответствует
точка на числовой
окружности
6
4
3
3
4
2
3
5
6
2
2
3
2
2
2
1
2
1 3 2 1
2
2
0
2
4
3
11
6
7
4
5 3
6
4
3
1
2
2
2
1
2
2
2
3
2
1
Далее
3 1
2
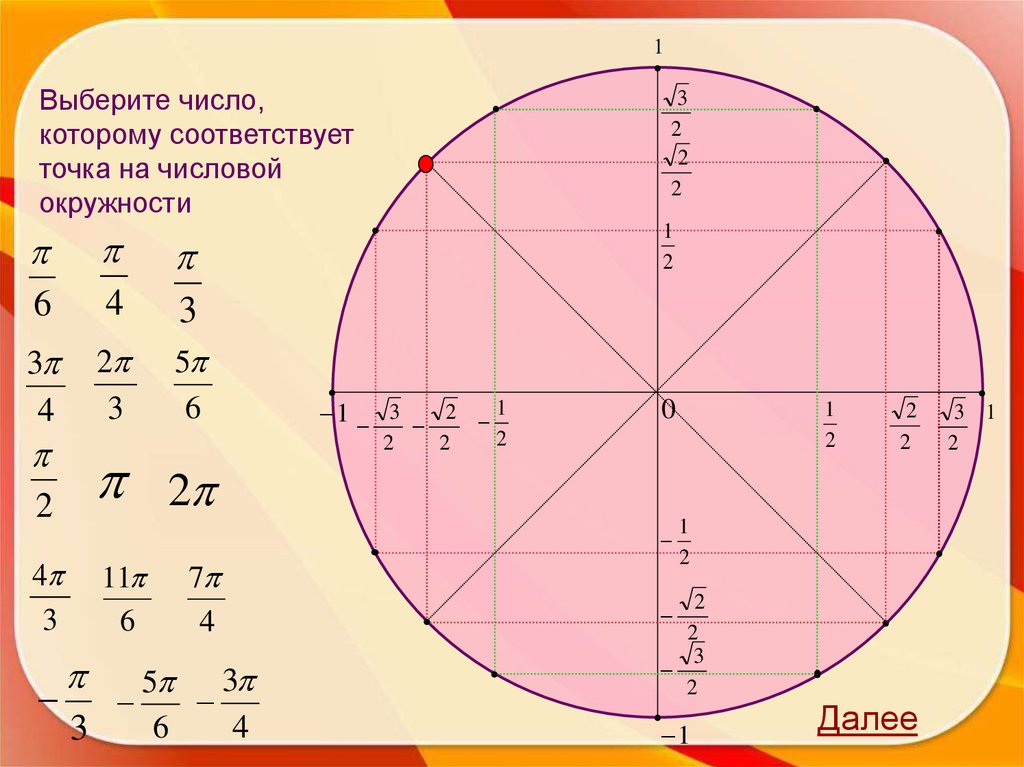
8.
1Выберите число,
которому соответствует
точка на числовой
окружности
6
4
3
3
4
2
3
5
6
2
2
3
2
2
2
1
2
1 3 2 1
2
2
0
2
4
3
11
6
7
4
5 3
6
4
3
1
2
2
2
1
2
2
2
3
2
1
Далее
3 1
2
9.
1Выберите число,
которому соответствует
точка на числовой
окружности
6
4
3
3
4
2
3
5
6
2
2
3
2
2
2
1
2
1 3 2 1
2
2
0
2
4
3
11
6
7
4
5 3
6
4
3
1
2
2
2
1
2
2
2
3
2
1
Далее
3 1
2
10.
1Выберите число,
которому соответствует
точка на числовой
окружности
6
4
3
3
4
2
3
5
6
2
2
3
2
2
2
1
2
1 3 2 1
2
2
0
2
4
3
11
6
7
4
5 3
6
4
3
1
2
2
2
1
2
2
2
3
2
1
Далее
3 1
2
11.
1Выберите число,
которому соответствует
точка на числовой
окружности
6
4
3
3
4
2
3
5
6
2
2
3
2
2
2
1
2
1 3 2 1
2
2
0
2
4
3
11
6
7
4
5 3
6
4
3
1
2
2
2
1
2
2
2
3
2
1
Далее
3 1
2
12.
1Выберите число,
которому соответствует
точка на числовой
окружности
6
4
3
3
4
2
3
5
6
2
2
3
2
2
2
1
2
1 3 2 1
2
2
0
2
4
3
11
6
7
4
5 3
6
4
3
1
2
2
2
1
2
2
2
3
2
1
Далее
3 1
2
13.
1Выберите число,
которому соответствует
точка на числовой
окружности
6
4
3
3
4
2
3
5
6
2
2
3
2
2
2
1
2
1 3 2 1
2
2
0
2
4
3
11
6
7
4
5 3
6
4
3
1
2
2
2
1
2
2
2
3
2
1
Далее
3 1
2
14.
1Выберите число,
которому соответствует
точка на числовой
окружности
6
4
3
3
4
2
3
5
6
2
2
3
2
2
2
1
2
1 3 2 1
2
2
0
2
4
3
11
6
7
4
5 3
6
4
3
1
2
2
2
1
2
2
2
3
2
1
Далее
3 1
2
15.
1Выберите число,
которому соответствует
точка на числовой
окружности
6
4
3
3
4
2
3
5
6
2
2
3
2
2
2
1
2
1 3 2 1
2
2
0
2
4
3
11
6
7
4
5 3
6
4
3
1
2
2
2
1
2
2
2
3
2
1
Далее
3 1
2
16.
1Выберите число,
которому соответствует
точка на числовой
окружности
6
4
3
3
4
2
3
5
6
2
2
3
2
2
2
1
2
1 3 2 1
2
2
0
2
4
3
11
6
7
4
5 3
6
4
3
1
2
2
2
1
2
2
2
3
2
1
Далее
3 1
2
17.
1Выберите число,
которому соответствует
точка на числовой
окружности
6
4
3
3
4
2
3
5
6
2
2
3
2
2
2
1
2
1 3 2 1
2
2
0
2
4
3
11
6
7
4
5 3
6
4
3
1
2
2
2
1
2
2
2
3
2
1
Далее
3 1
2
18.
1Выберите число,
которому соответствует
точка на числовой
окружности
6
4
3
3
4
2
3
5
6
2
2
3
2
2
2
1
2
1 3 2 1
2
2
0
2
4
3
11
6
7
4
5 3
6
4
3
1
2
2
2
1
2
2
2
3
2
1
Далее
3 1
2
19.
1Выберите число,
которому соответствует
точка на числовой
окружности
6
4
3
3
4
2
3
5
6
2
2
3
2
2
2
1
2
1 3 2 1
2
2
0
2
4
3
11
6
7
4
5 3
6
4
3
1
2
2
2
1
2
2
2
3
2
1
Далее
3 1
2
20.
Вы можете выйти изтренажера, перейти на
главную страницу или начать
заново
Выберите нужное действие
Начать заново
Перейти на главную
Выход
21. Тренажер по тригонометрии
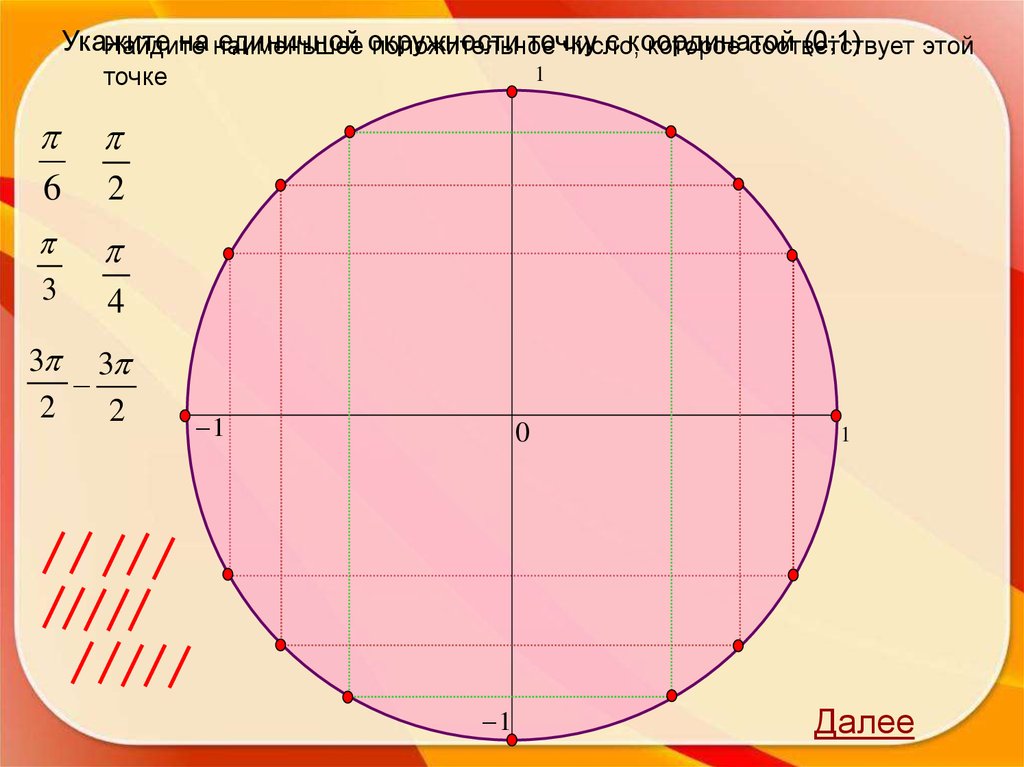
«Тригонометрический круг 2»22.
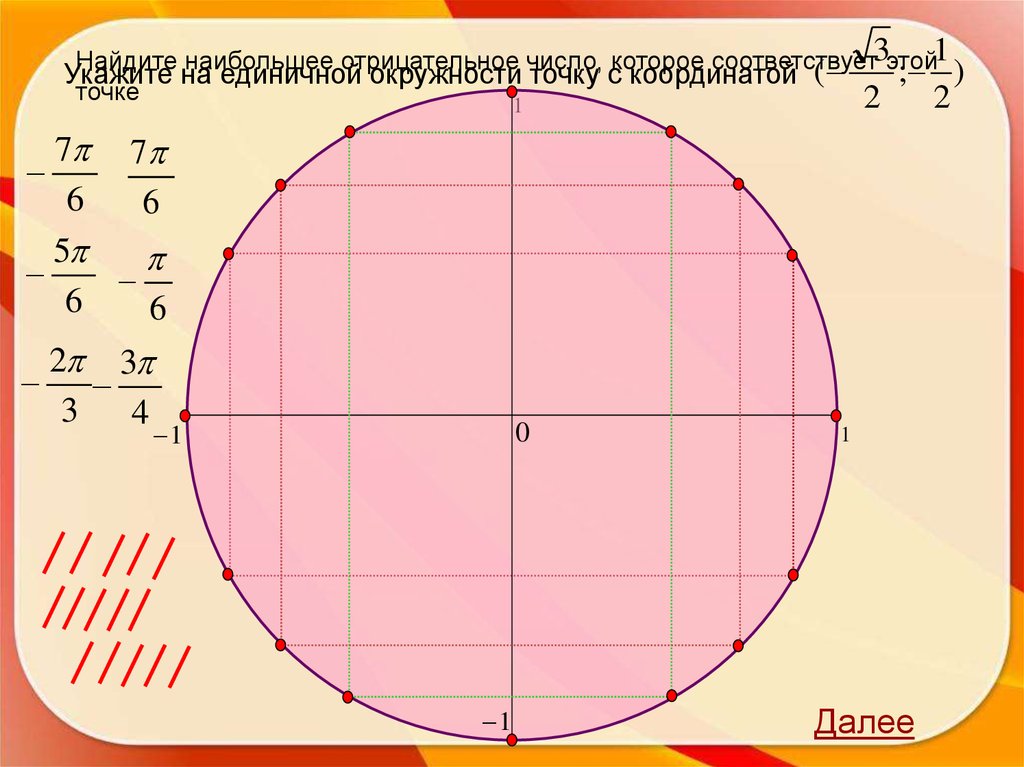
Укажитена наименьшее
единичной окружности
точку
с координатой
(0;1)
Найдите
положительное
число,
которое соответствует
этой
точке
6
2
3
4
3 3
2
2
1
1
0
1
1
Далее
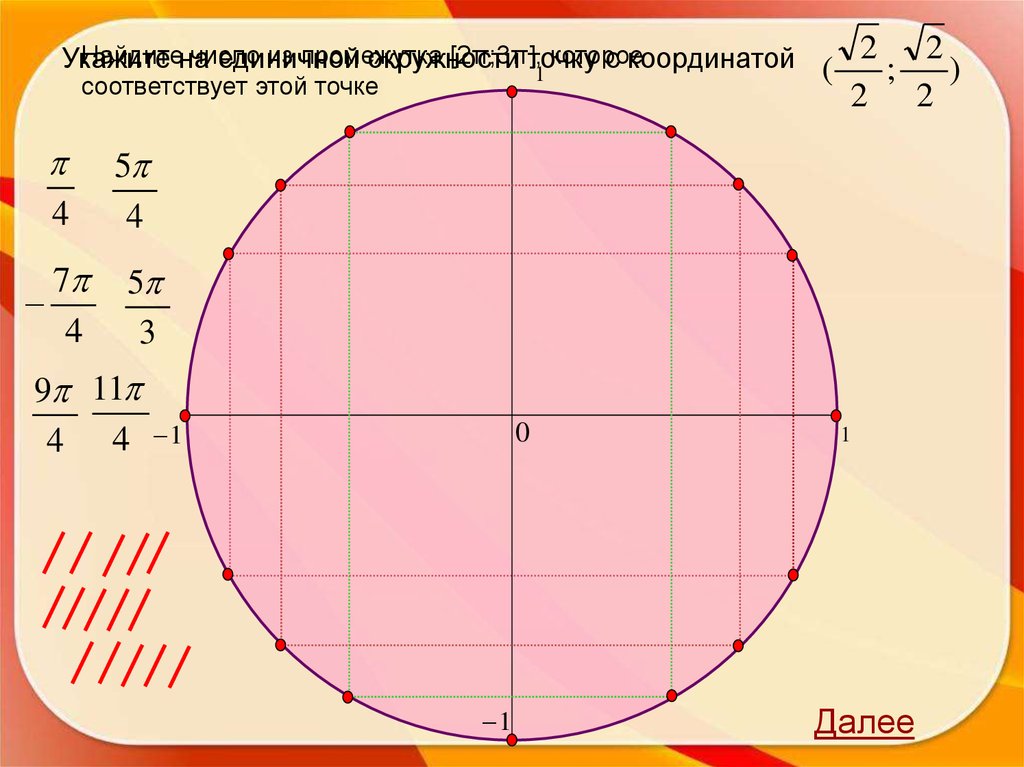
23.
2Найдитена
число
из промежутка
[2π;3π],
которое
Укажите
единичной
окружности
точку
с
координатой
(
;
1
соответствует этой точке
4
7
4
2
5
4
5
3
9 11
4 4
1
0
1
1
Далее
2
)
2
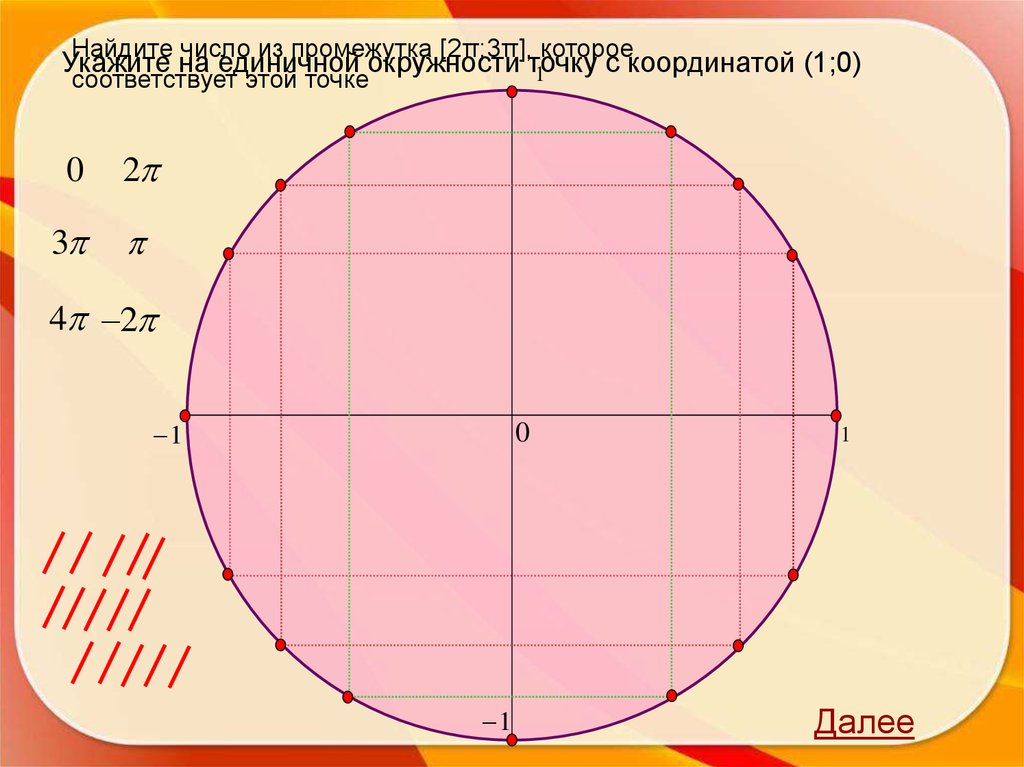
24.
Найдите число из промежутка [2π;3π], котороесоответствует этой точке
Укажите на единичной окружности точку
с координатой (1;0)
1
0
2
3
4 2
1
0
1
1
Далее
25.
3 этой1
Найдитена
наименьшее
положительное
число,скоторое
соответствует
Укажите
единичной
окружности точку
координатой
(
;
)
1
точке
2 2
11
3
6
5
6
6
5
3
4
1
0
1
1
Далее
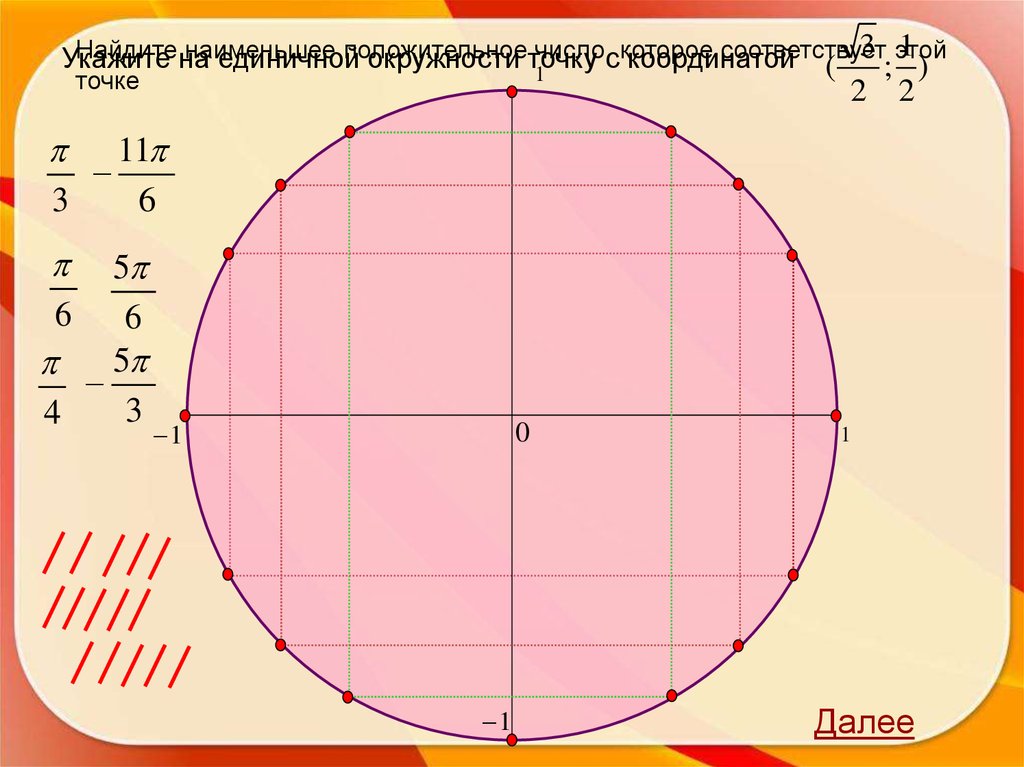
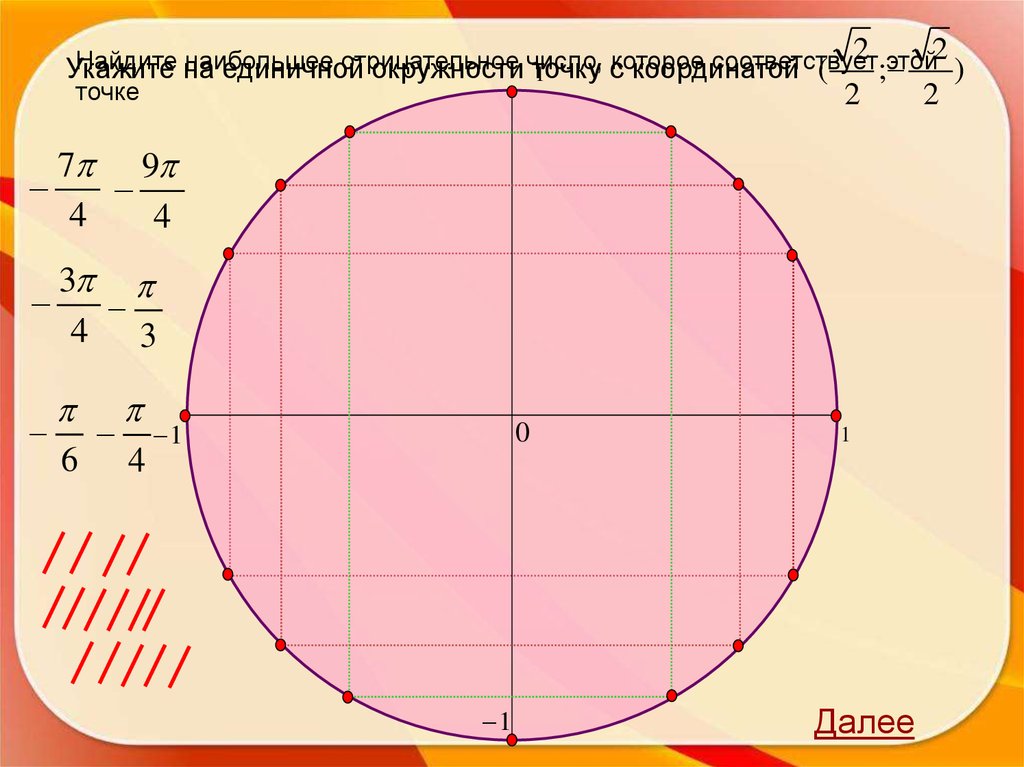
26.
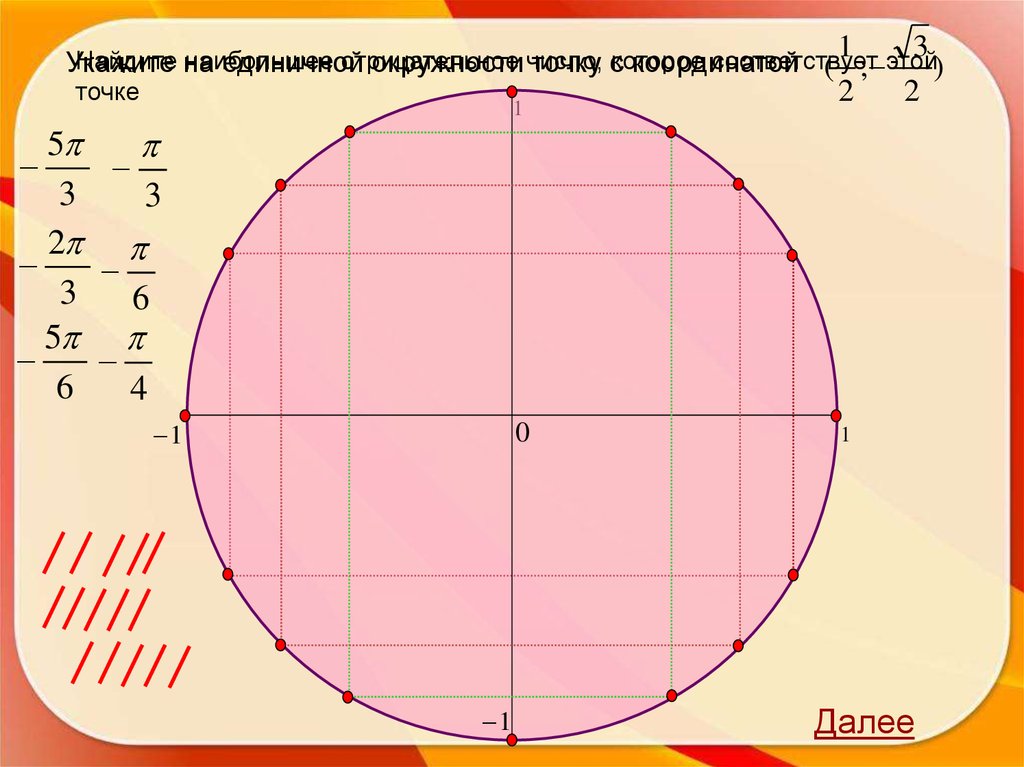
2 этой2Найдите
наибольшее
отрицательное
число,
которое
соответствует
Укажите на единичной окружности точку
с координатой (
;
)
1
точке
2
2
7 9
4
4
3
4 3
1
6 4
0
1
1
Далее
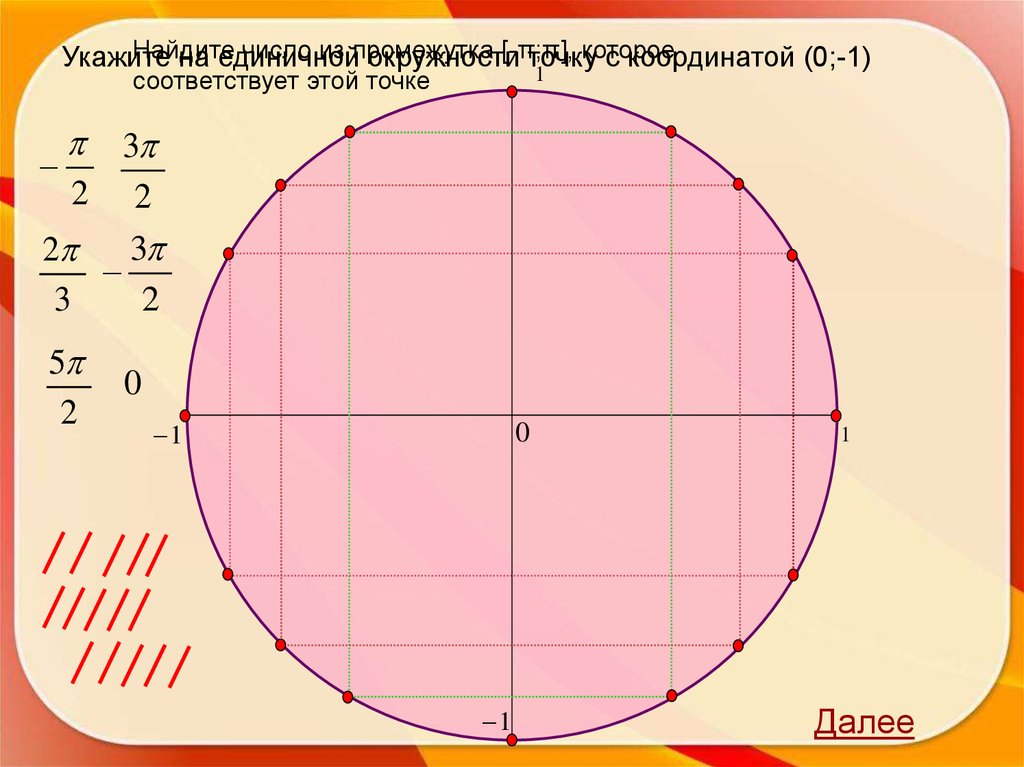
27.
Найдитечисло из промежутка
[-π;π],
которое
Укажите
на единичной
окружности
точку
с координатой (0;-1)
1
соответствует этой точке
3
2 2
3
2
2
3
5
2
0
1
0
1
1
Далее
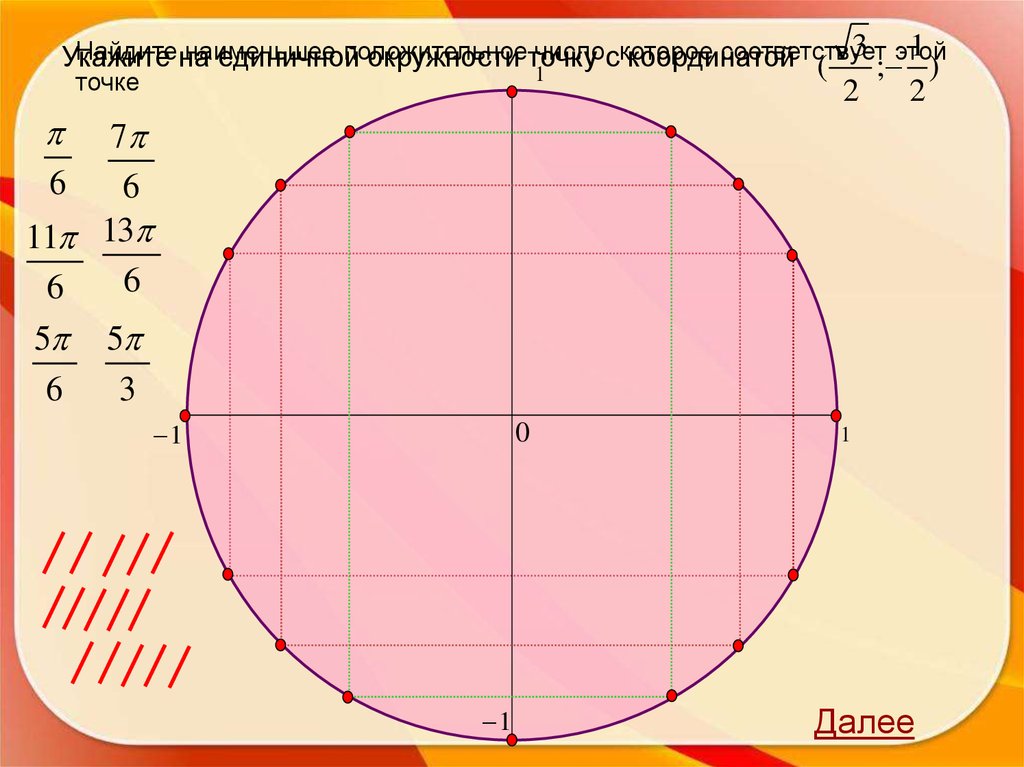
28.
3 этой1
Найдитена
наименьшее
положительное
число,скоторое
соответствует
Укажите
единичной
окружности точку
координатой
(
;
)
1
точке
2
7
6
6
11 13
6
6
5 5
6
3
1
0
1
2
1
Далее
29.
13
Найдите на
число
из промежутка
[3π;4π],точку
которое
Укажите
единичной
окружности
с
координатой
(
;
)
1
2
2
соответствует этой точке
4 10
3
3
7 19
6 6
11 2
3
4
1
0
1
1
Далее
30.
Найдите наименьшее положительное число, которое соответствует2 этой
2
Укажите на единичной окружности точку
с координатой (
1
точке
4
5
4
7
4
3
4
5 3
4
4
1
0
1
2
;
1
Далее
2
)
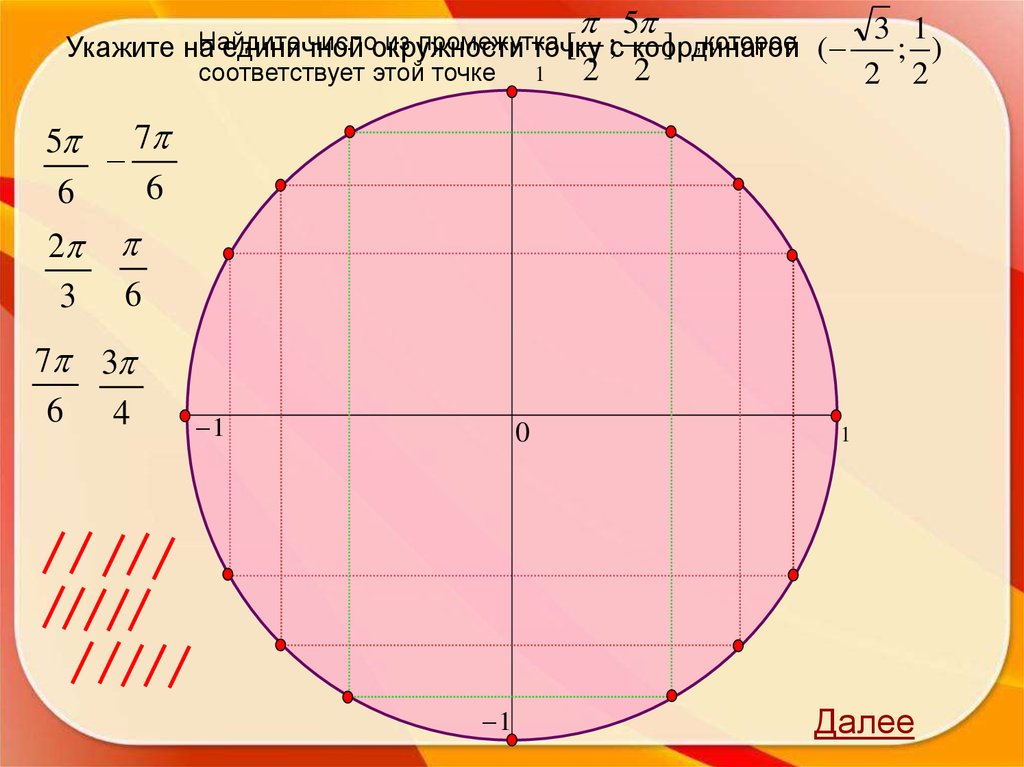
31.
Найдите числоиз промежутка
[5π;7π),точку
которое
Укажите
на единичной
окружности
с координатой (-1;0)
1
соответствует этой точке
7
6 11
2
5 6,5
1
0
1
1
Далее
32.
3этой1Найдите наибольшее отрицательное число, которое соответствует
; )
Укажите на единичной окружности точку с координатой (
точке
2
2
1
7 7
6
6
5
6
6
2 3
3
4
1
0
1
1
Далее
33.
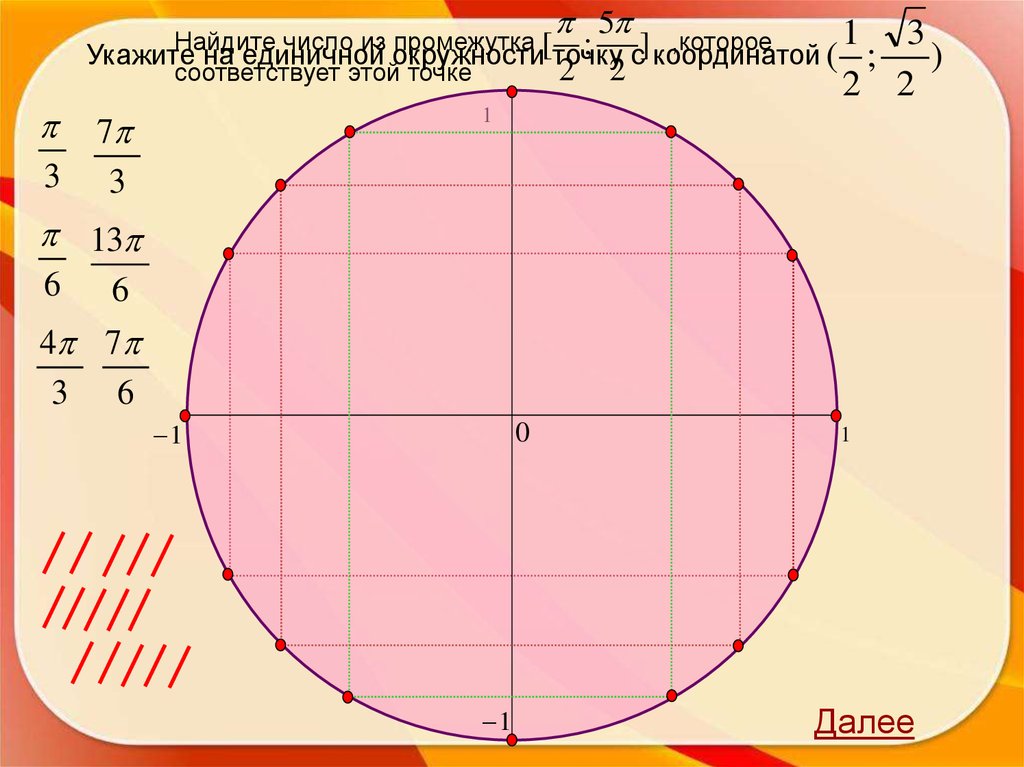
5Найдите
числоокружности
из промежутка
[ ;с координатой
] ,которое
Укажите на
единичной
точку
соответствует этой точке 1 2 2
(
3 1
; )
2 2
7
5
6
6
2
3 6
7 3
6 4
1
0
1
1
Далее
34.
51
Найдите число из промежутка [ ;
,которое
Укажите
на единичной окружности точку с] координатой
( ;
2 2
соответствует этой точке
7
3 3
13
6 6
3
)
2 2
1
4 7
3 6
1
0
1
1
Далее
35.
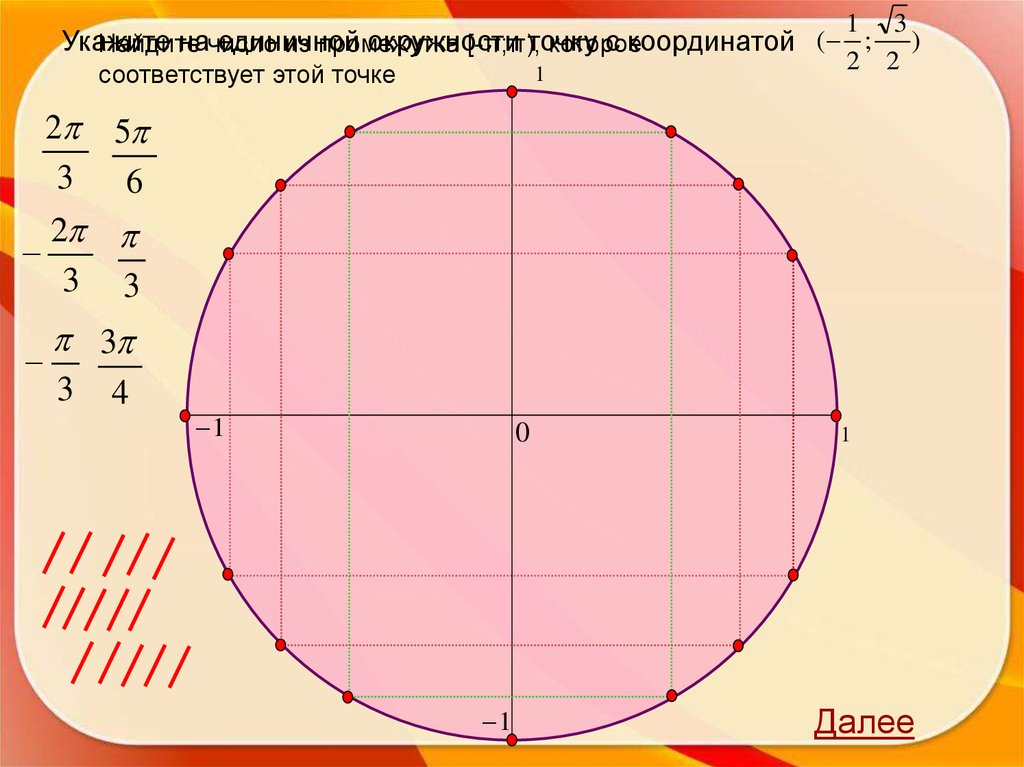
1 3(
; )
Укажите
начисло
единичной
окружности
точку
с координатой
Найдите
из промежутка
[-π;π),
которое
2 2
1
соответствует этой точке
2 5
3 6
2
3 3
3
3 4
1
0
1
1
Далее
36.
2 23
(
;
)
Найдите
из промежутка
Укажите
начисло
единичной
окружности
координатой
[ точку
; ]с,которое
2 2
2
2
соответствует этой точке
3
4
4
1
3
5
2
4
5
6
7
4
1
0
1
1
Далее
37.
12
3
2
Найдите на
наибольшее
отрицательное
соответствует
Укажите
единичной
окружности число,
точку скоторое
координатой
( ; этой)
точке
1
5
3
3
2
3
6
5
6
4
1
0
1
1
Далее
38.
Вы можете выйти изтренажера или начать заново
Выберите нужное действие
Начать заново
Перейти на главную
Выход
39. Тренажер
«Знаки тригонометрическихфункций»
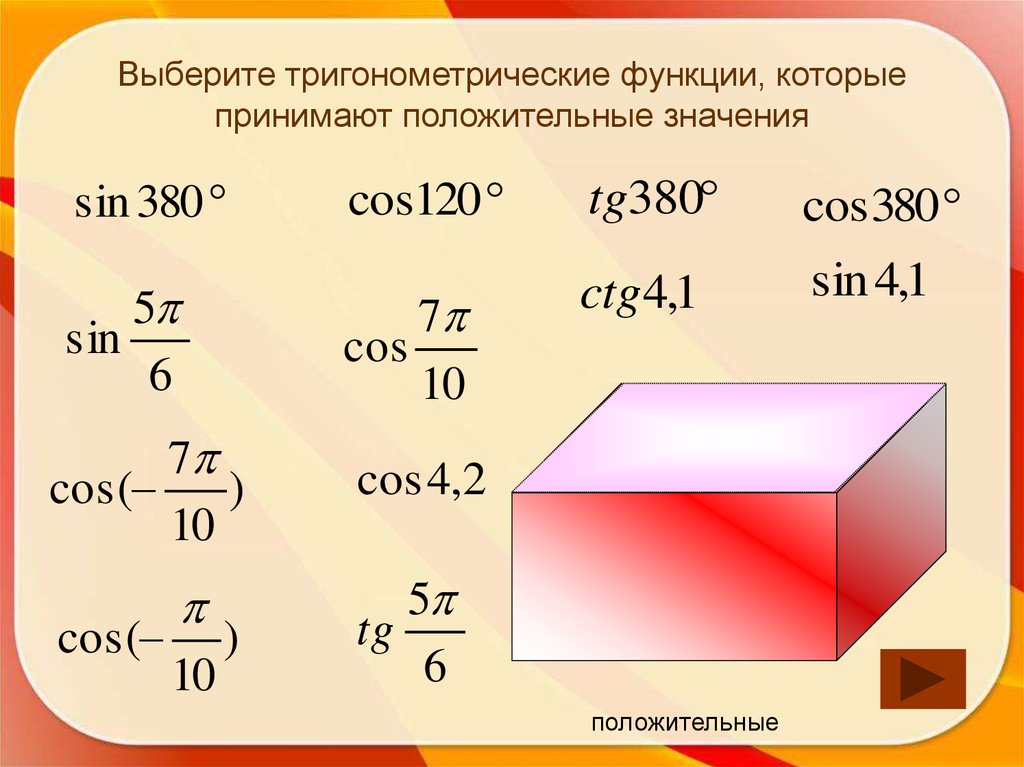
40. Выберите тригонометрические функции, которые принимают положительные значения
sin 3805
sin
6
7
cos(
)
10
cos(
10
)
cos120
tg380
cos 380
7
cos
10
ctg 4,1
sin 4,1
cos 4,2
5
tg
6
положительные
41. Выберите тригонометрические функции, которые принимают отрицательные значения
sin( 50 )2
cos
3
2
sin
3
cos( 200 )
cos( 45 )
tg ( 50 )
7
cos
10
ctg2
cos 4,2
tg
3
отрицательные
2
tg
3
sin 300
42. Выберите те значения аргумента , при которых произведение будет принимать положительное значение
Выберите те значения аргумента , при которых произведениеsin cos tg ctg будет принимать положительное значение
160º
2
3
210
3
4
3,8
9
4
6,1
4
3
2,2
5
6
70º
5
4
280º
Ошибка!
6,4
sin cos tg ctg 0
720º
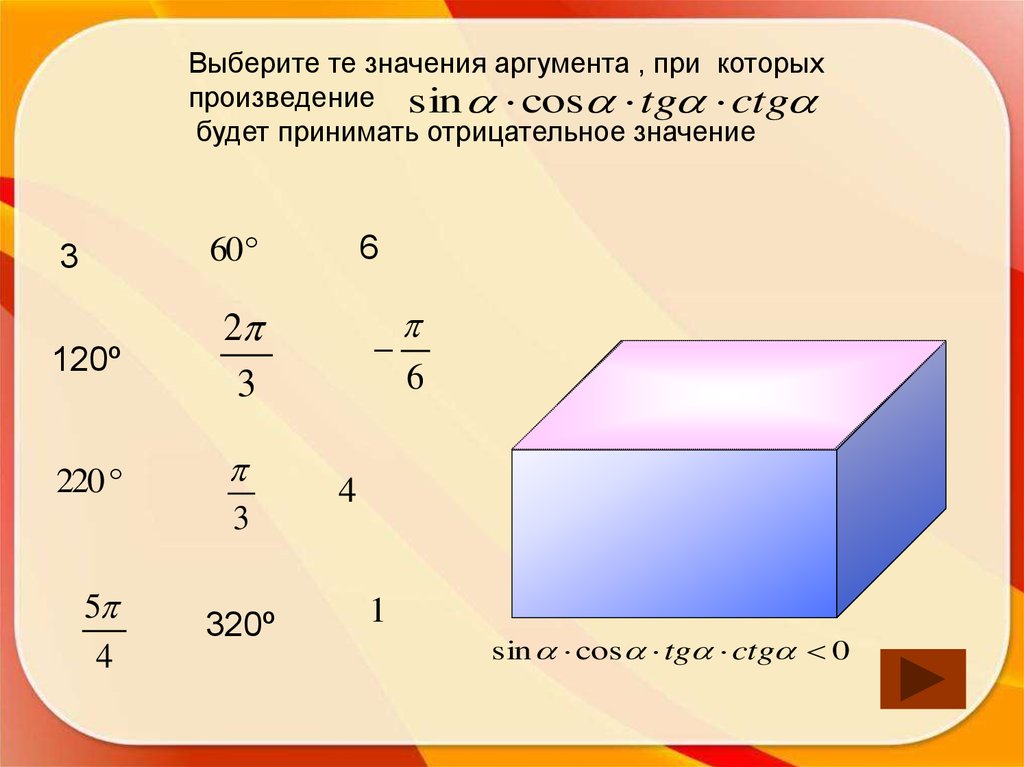
43. Выберите те значения аргумента , при которых произведение будет принимать отрицательное значение
Выберите те значения аргумента , при которыхпроизведение sin cos tg ctg
будет принимать отрицательное значение
60
3
120º
2
3
220
3
5
4
320º
6
6
4
1
sin cos tg ctg 0
44. Известно, что . Выберите те тригонометрические функции, которые принимают положительные значения.
Известно, что(0; ) . Выберите те тригонометрические
4
функции, которые принимают положительные значения.
Сделайте клик мышью в ячейках, удовлетворяющих условию.
sin
cos
tg
ctg
-
3
2
+
2
3
2
3
2
3
2
+
-
2
2
2
-
+
-
2
+
+
2
-
2
+
+
+
2
В случае правильного ответа в ячейке появляется знак «+»,
неправильного – знак «-»
45. Известно, что . Выберите те тригонометрические функции, которые принимают отрицательные значения.
Известно, что(0; ) . Выберите те тригонометрические
4
функции, которые принимают отрицательные значения.
Сделайте клик мышью в ячейках, удовлетворяющих условию.
sin
cos
tg
ctg
-
3
2
2
+
2
3
2
3
2
3
2
2
2
-
2
+
+
+
2
-
+
2
-
+
+
+
2
В случае правильного ответа в ячейке появляется знак
«+», неправильного – знак «-»
46.
Вы можете выйти изтренажера, начать заново или
перейти на главную страницу
Выберите нужное действие
Начать заново
Перейти на главную
Выход
47. Тренажер
«Таблица значенийarcsin,arccos»
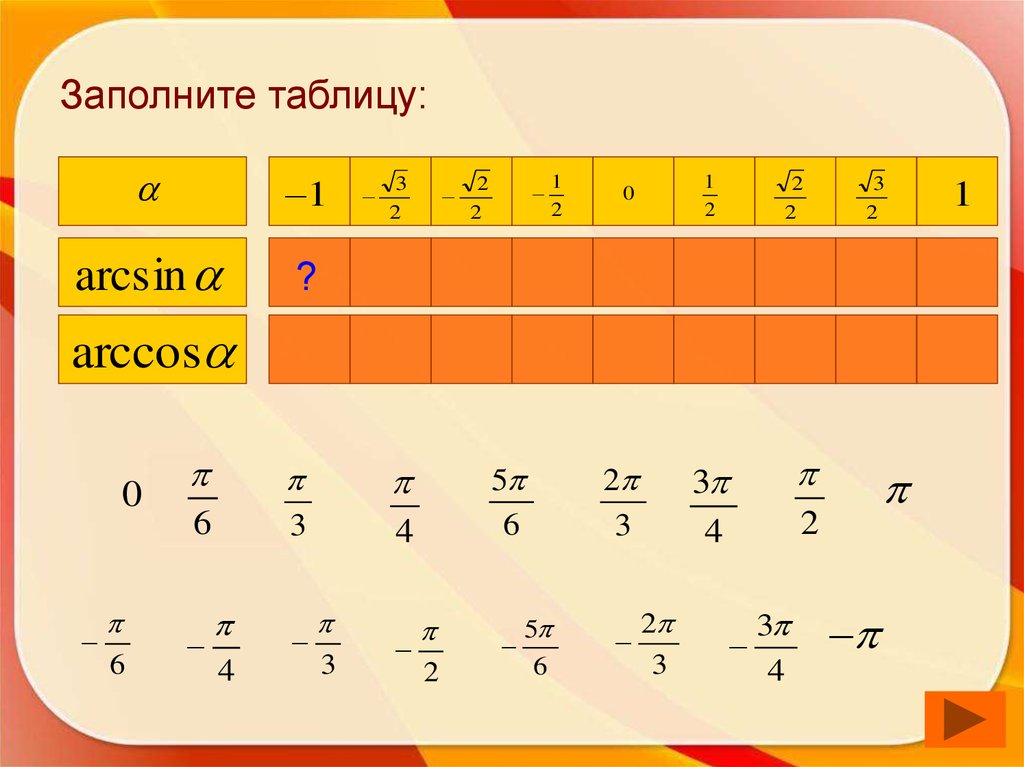
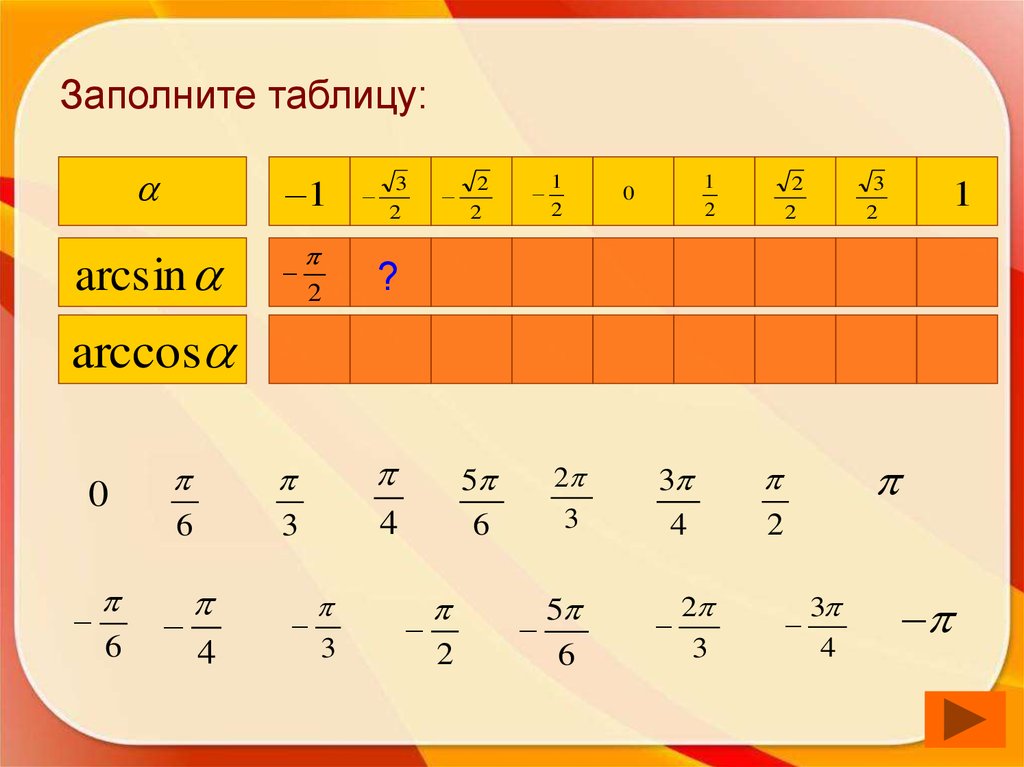
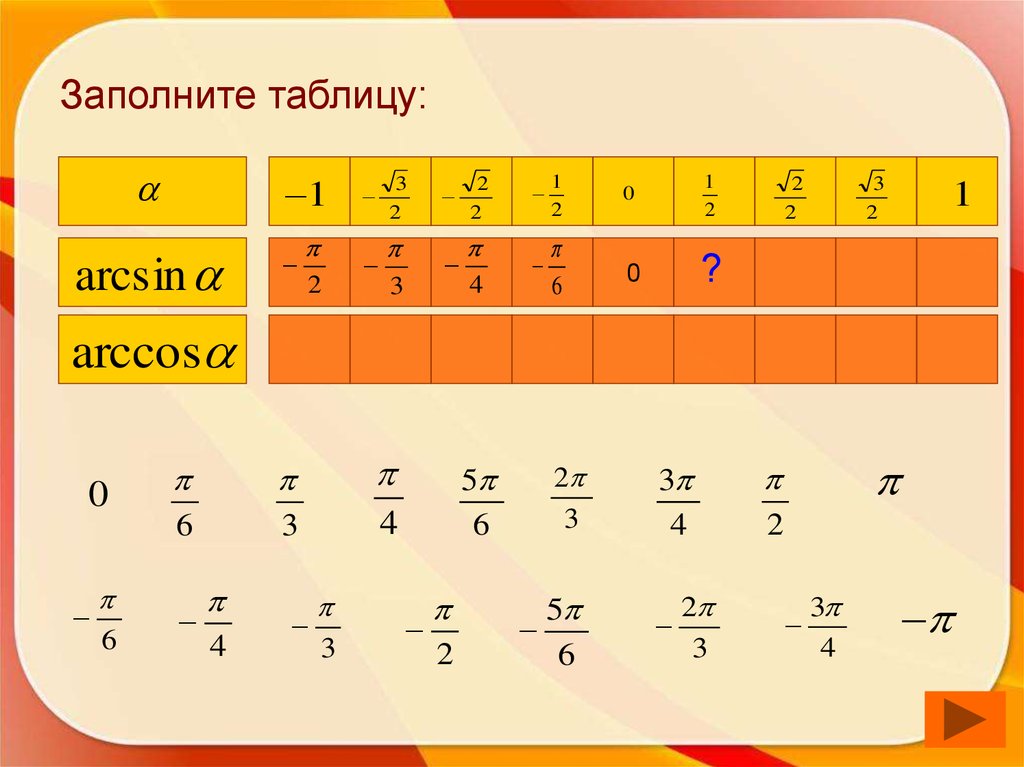
48. Заполните таблицу:
1arcsin
?
3
2
2
2
1
2
1
2
0
2
2
3
2
arccos
0
6
6
3
4
4
3
5
6
2
5
6
3
4
2
3
2
3
2
3
4
1
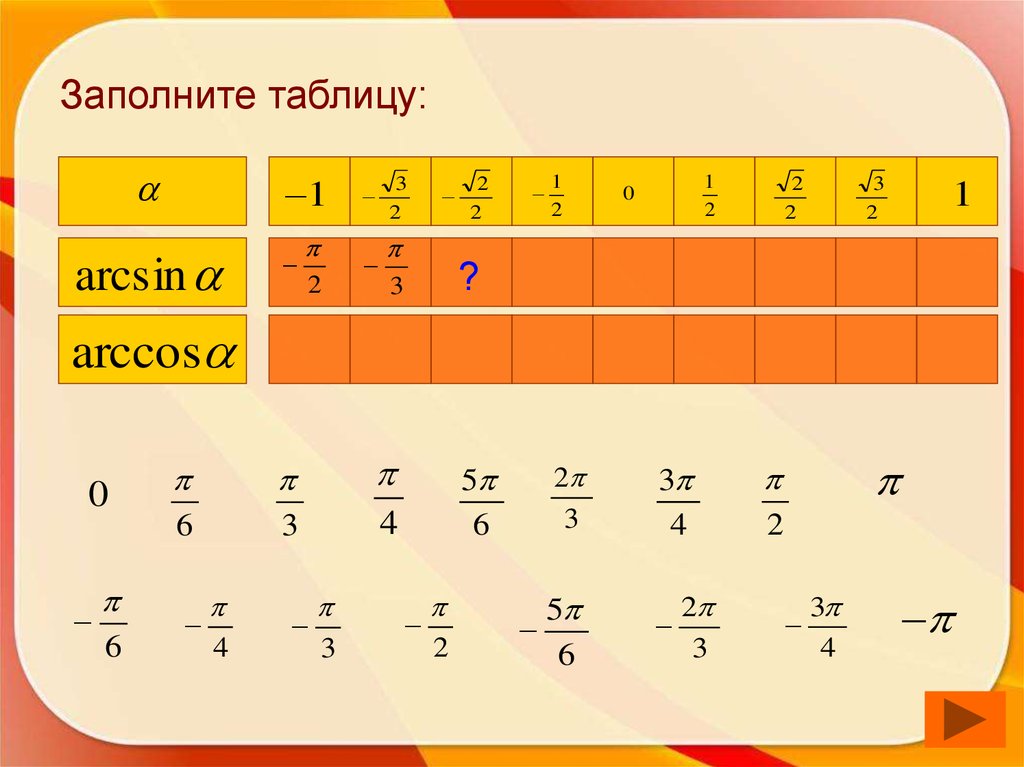
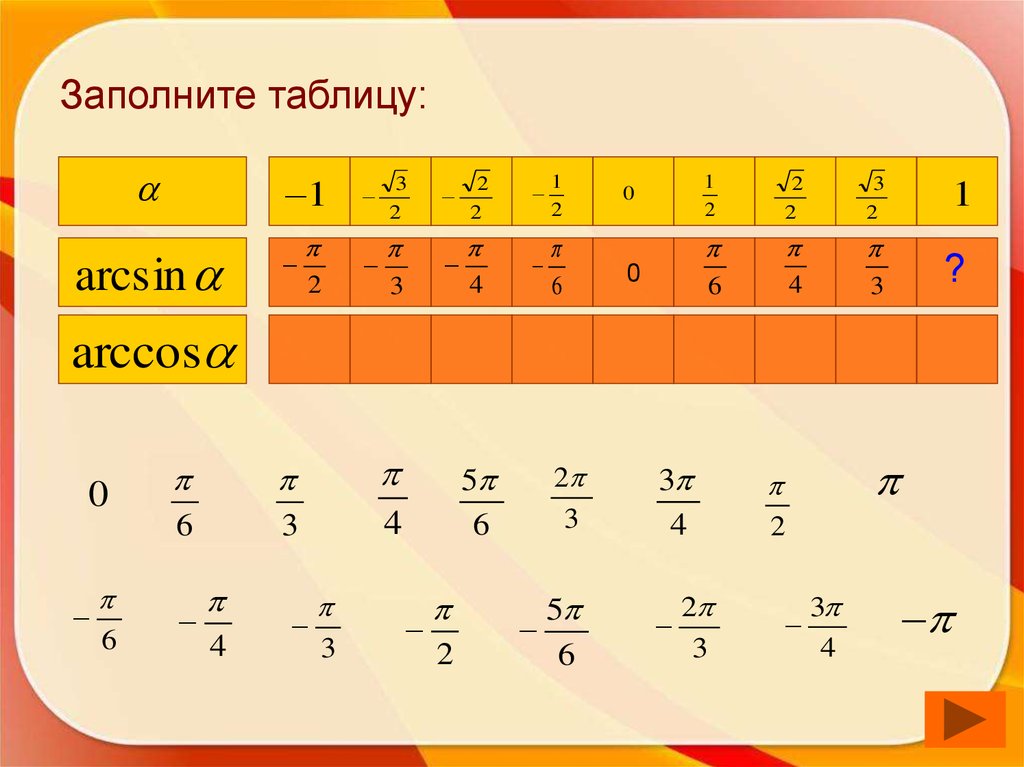
49. Заполните таблицу:
1arcsin
2
3
2
2
2
1
2
1
2
0
2
2
3
2
1
?
arccos
0
6
6
3
4
4
3
5
6
2
2
3
5
6
3
4
2
3
2
3
4
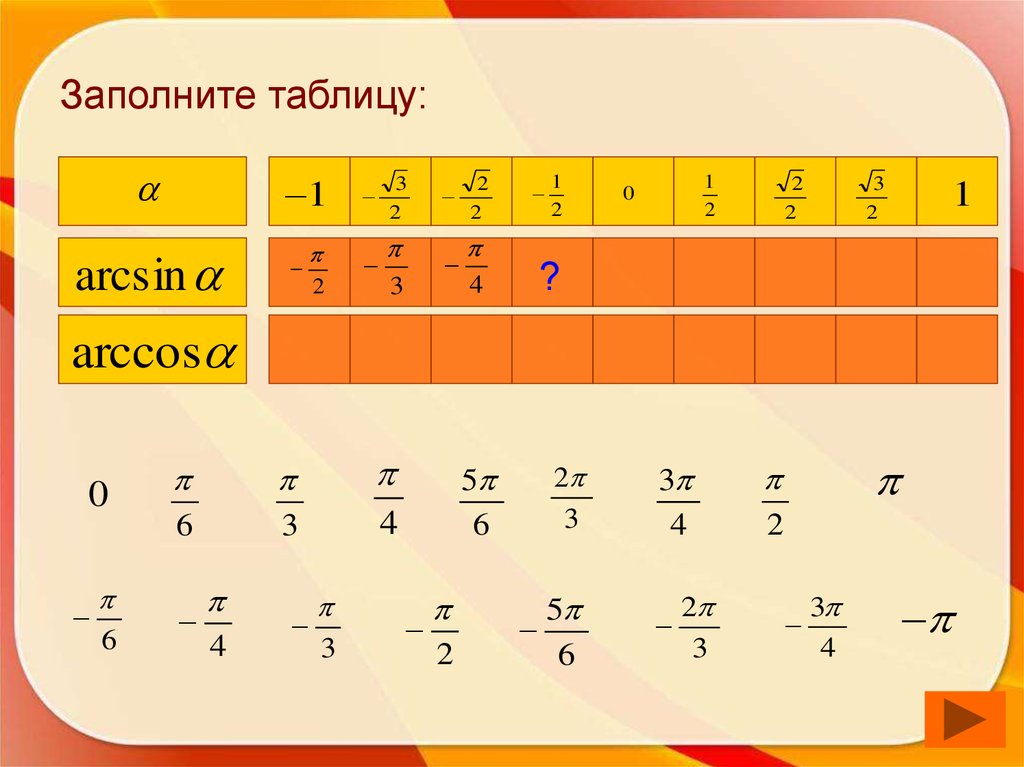
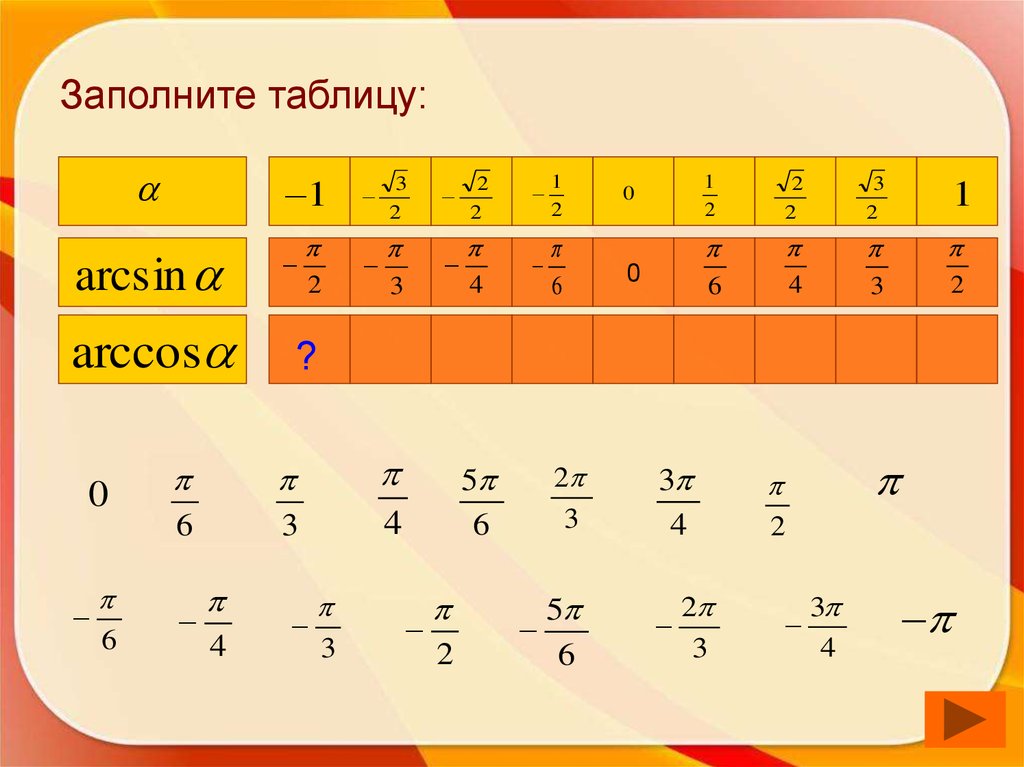
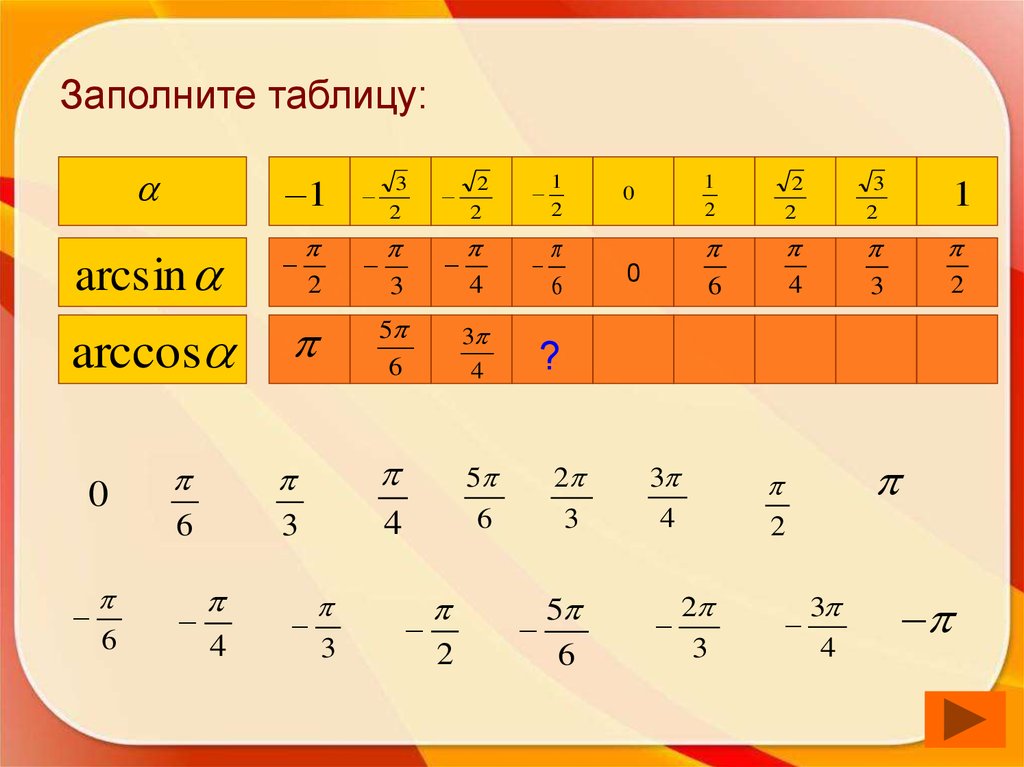
50. Заполните таблицу:
1arcsin
2
3
2
2
2
1
2
1
2
0
2
2
3
2
1
?
3
arccos
0
6
6
3
4
4
3
5
6
2
2
3
5
6
3
4
2
3
2
3
4
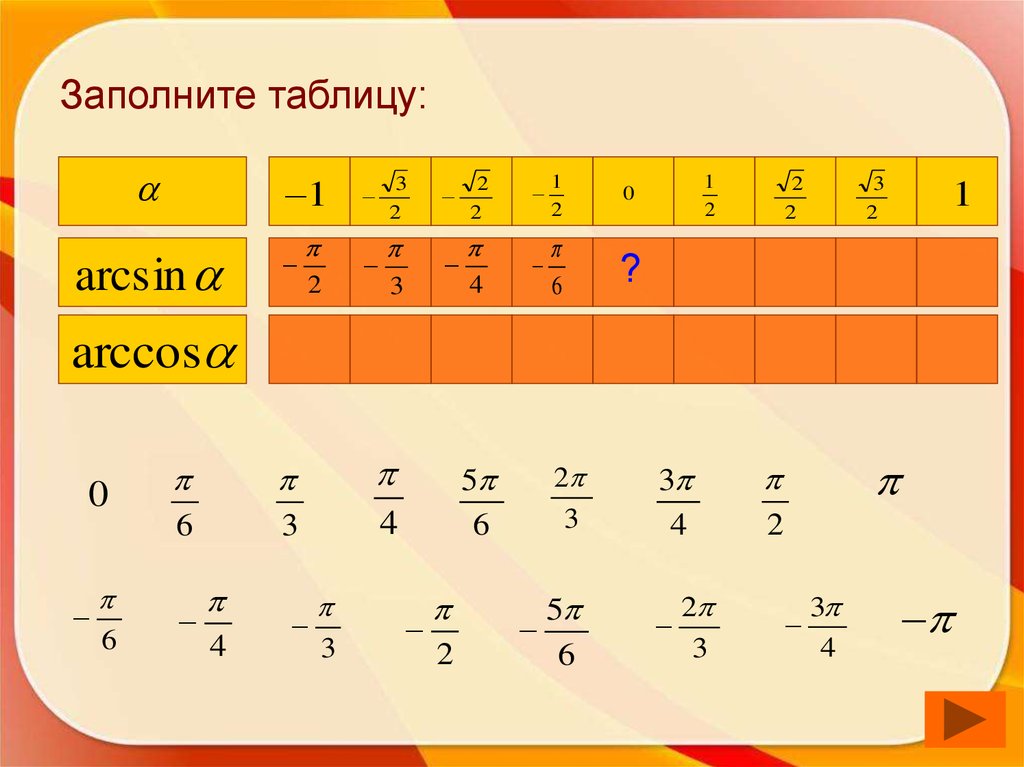
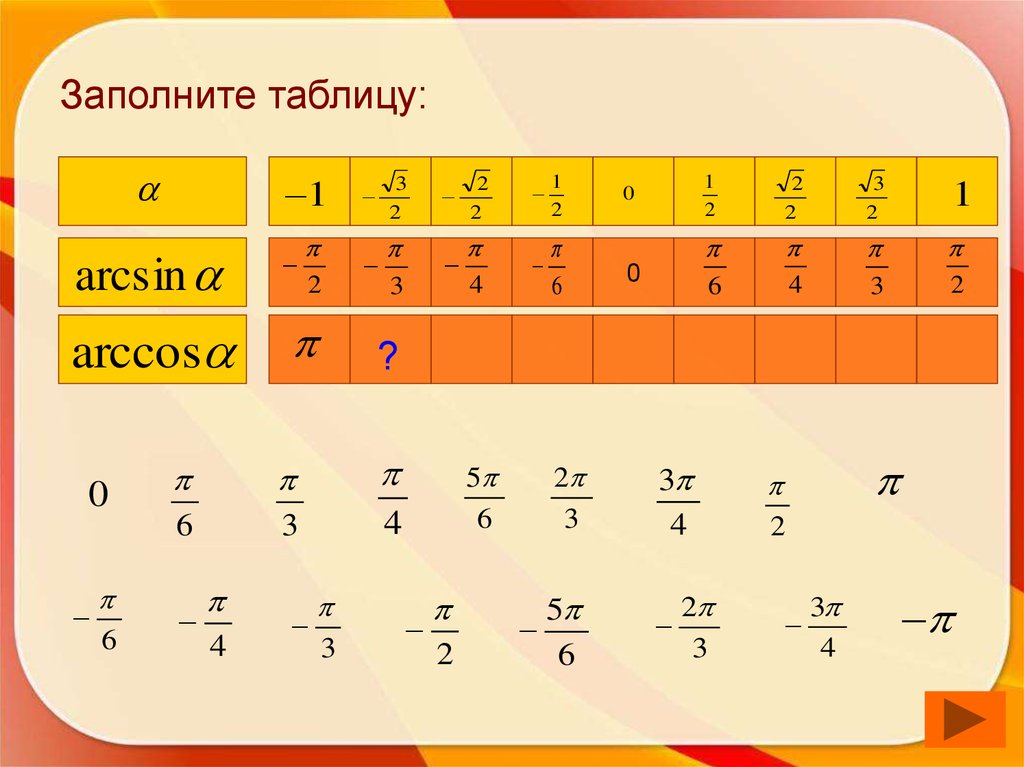
51. Заполните таблицу:
1arcsin
2
3
2
3
2
2
4
1
2
1
2
0
2
2
3
2
1
?
arccos
0
6
6
3
4
4
3
5
6
2
2
3
5
6
3
4
2
3
2
3
4
52. Заполните таблицу:
1arcsin
2
3
2
3
2
2
4
1
2
0
6
?
1
2
2
2
3
2
1
arccos
0
6
6
3
4
4
3
5
6
2
2
3
5
6
3
4
2
3
2
3
4
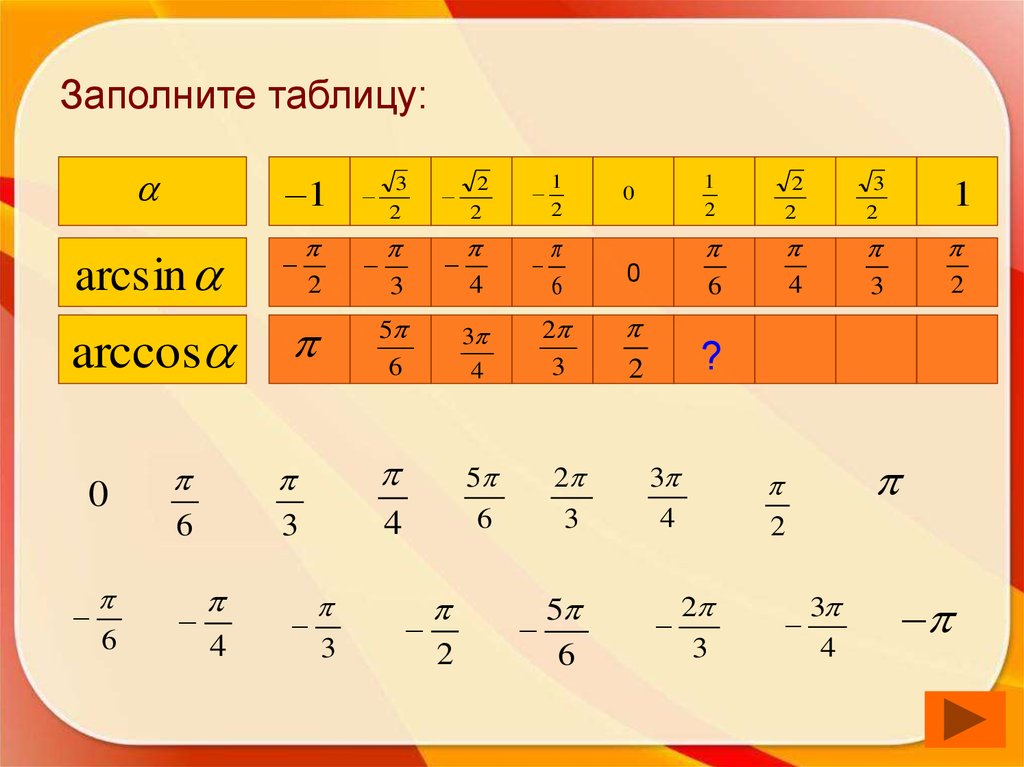
53. Заполните таблицу:
1arcsin
2
3
2
3
2
2
4
1
2
6
0
1
2
0
?
2
2
3
2
1
arccos
0
6
6
3
4
4
3
5
6
2
2
3
5
6
3
4
2
3
2
3
4
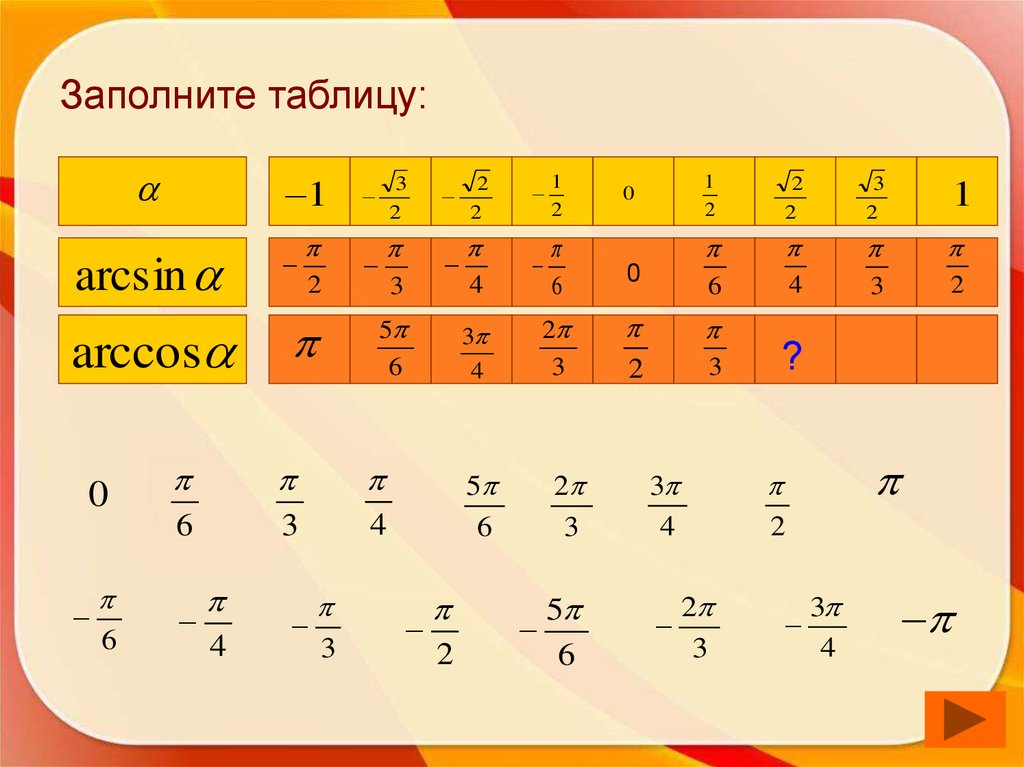
54. Заполните таблицу:
1arcsin
2
3
2
3
2
2
4
1
2
6
1
2
0
2
2
0
3
2
1
?
6
arccos
0
6
6
3
4
4
3
5
6
2
2
3
5
6
3
4
2
3
2
3
4
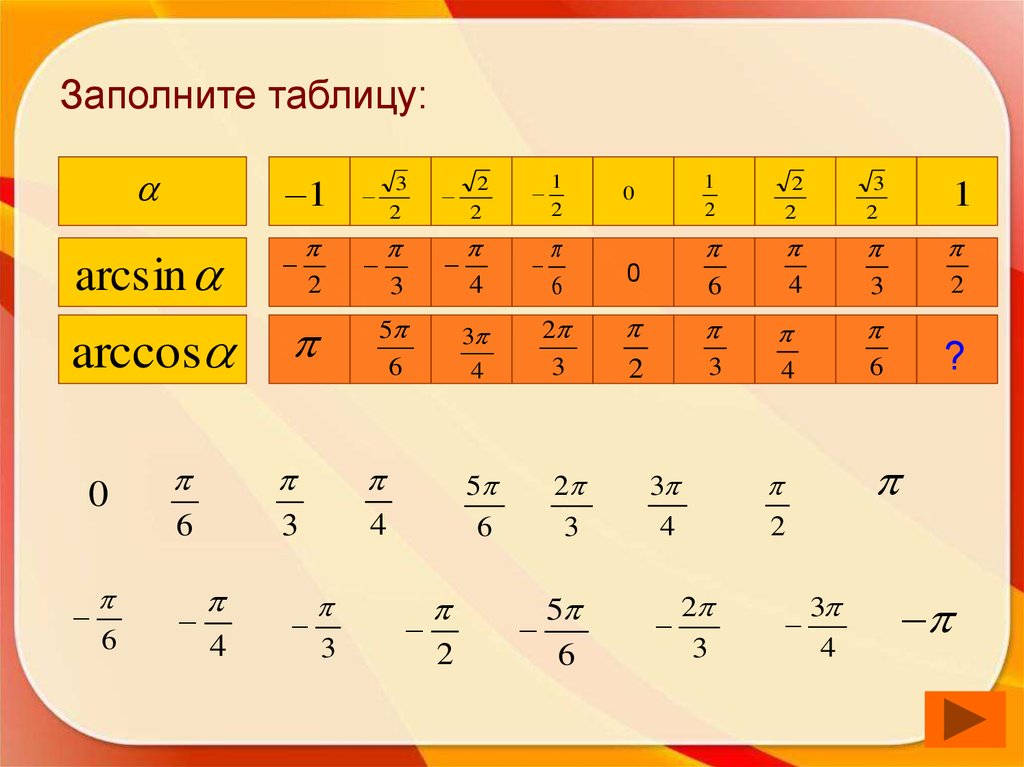
55. Заполните таблицу:
1arcsin
2
3
2
3
2
2
4
1
2
6
0
0
1
2
2
2
6
4
3
2
1
?
arccos
0
6
6
3
4
4
3
5
6
2
2
3
5
6
3
4
2
3
2
3
4
56. Заполните таблицу:
1arcsin
2
3
2
3
2
2
4
1
2
6
0
0
1
2
2
2
3
2
6
4
3
1
?
arccos
0
6
6
3
4
4
3
5
6
2
2
3
5
6
3
4
2
3
2
3
4
57. Заполните таблицу:
1arcsin
arccos
0
6
2
3
2
6
3
4
4
2
2
4
1
2
6
0
0
1
2
2
2
3
2
1
6
4
3
2
?
3
3
5
6
2
2
3
5
6
3
4
2
3
2
3
4
58. Заполните таблицу:
1arcsin
arccos
0
6
2
3
2
6
3
4
4
2
2
4
1
2
6
0
0
1
2
2
2
3
2
1
6
4
3
2
?
3
3
5
6
2
2
3
5
6
3
4
2
3
2
3
4
59. Заполните таблицу:
1arcsin
arccos
0
6
2
3
2
3
6
3
4
4
5
6
3
2
2
4
1
2
6
0
0
1
2
2
2
3
2
1
6
4
3
2
?
5
6
2
2
3
3
4
5
6
2
2
3
3
4
60. Заполните таблицу:
1arcsin
arccos
0
6
2
3
2
3
4
4
3
4
5
6
6
3
4
2
2
5
6
3
2
1
2
6
0
0
1
2
2
2
3
2
1
6
4
3
2
?
2
3
3
4
5
6
2
2
3
3
4
61. Заполните таблицу:
1arcsin
arccos
0
6
2
3
2
3
4
4
3
4
5
6
6
3
4
2
2
5
6
3
2
1
2
6
0
2
3
?
0
2
3
3
4
5
6
1
2
2
2
3
2
1
6
4
3
2
2
2
3
3
4
62. Заполните таблицу:
1arcsin
arccos
0
6
2
3
2
3
4
4
3
4
5
6
6
3
4
2
2
5
6
3
2
1
2
6
2
3
0
0
1
2
2
2
3
2
1
6
4
3
2
?
2
2
3
3
4
5
6
2
2
3
3
4
63. Заполните таблицу:
1arcsin
arccos
0
6
2
3
2
5
6
6
3
4
4
3
3
2
2
4
3
4
5
6
2
1
2
6
2
3
1
2
2
2
3
2
1
0
6
4
3
2
2
3
0
2
3
3
4
5
6
?
2
2
3
3
4
64. Заполните таблицу:
1arcsin
arccos
0
6
2
3
2
5
6
6
3
4
4
3
3
2
2
4
3
4
5
6
2
1
2
6
2
3
1
2
2
2
3
2
1
0
6
4
3
2
2
3
4
?
0
2
3
3
4
5
6
2
2
3
3
4
65. Заполните таблицу:
1arcsin
arccos
0
6
2
3
2
5
6
6
3
4
4
3
3
2
2
4
3
4
5
6
2
1
2
6
2
3
1
2
2
2
3
2
1
0
6
4
3
2
2
3
4
6
0
2
3
3
4
5
6
?
2
2
3
3
4
66. Заполните таблицу:
1arcsin
arccos
2
Начать заново
3
2
3
5
6
2
2
4
3
4
1
2
6
2
3
1
2
2
2
3
2
1
0
6
4
3
2
2
3
4
6
0
Выход
Перейти на главную
0
67. Тренажер
Обратные тригонометрическихфункций
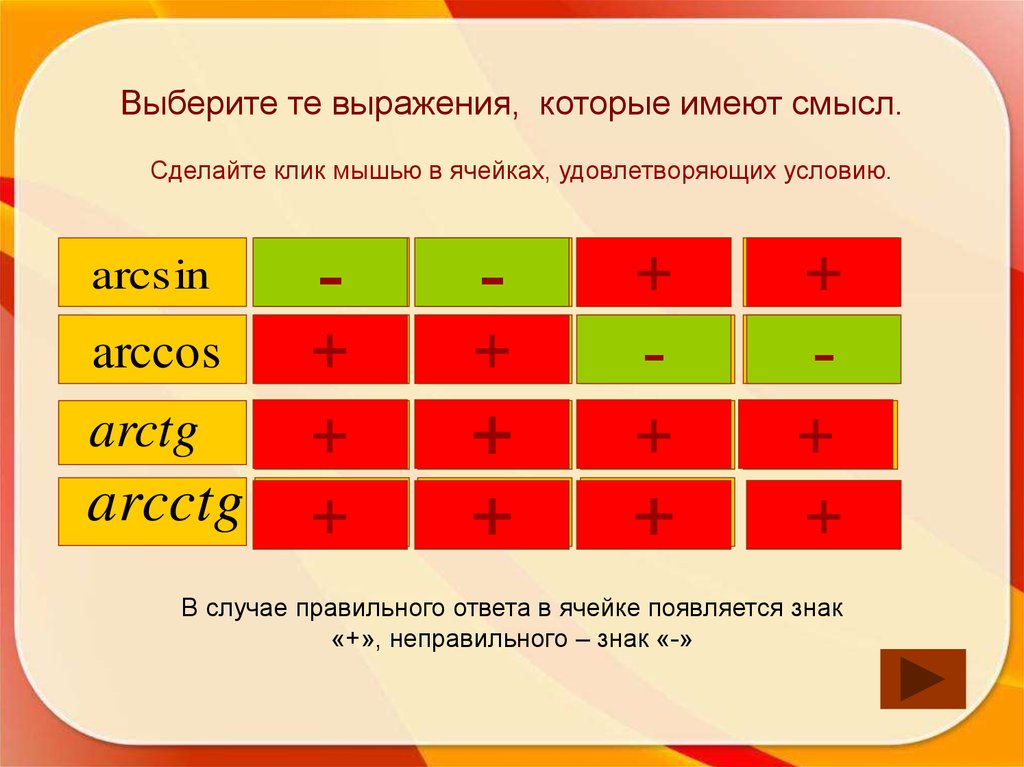
68. Выберите те выражения, которые имеют смысл.
Сделайте клик мышью в ячейках, удовлетворяющих условию.arcsin
1
3
+
-
arccos
1,5
-
+
+5
arcctg +
+
+
arctg
1
2
1,6
2
5
1,4
3
5
3
+
2
+5
2
3
+
7
+
-5
+2
1,9
+
В случае правильного ответа в ячейке появляется знак «+»,
неправильного – знак «-»
3
2
69. Выберите те выражения, которые имеют смысл.
Сделайте клик мышью в ячейках, удовлетворяющих условию.arcsin
-
3 20
3 1
4
5
+
3 2
2
+
+
+
arctg
+
arcctg +
arccos
-
5
2
2
3
7
2
+
+
4 20
3
2
1
3
+
+
+
+
2
4
3
2
3
3 17
В случае правильного ответа в ячейке появляется знак
«+», неправильного – знак «-»
70.
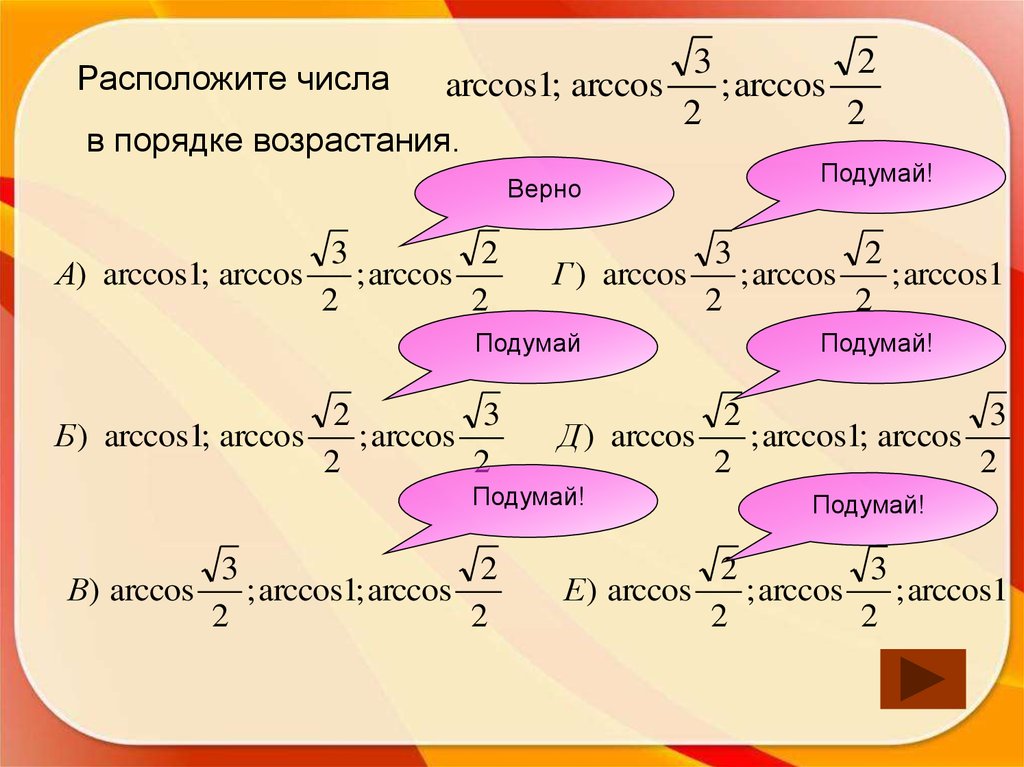
Расположите числа1
3
2
arcsin ; arcsin
; arcsin
2
2
2
в порядке возрастания.
Подумай!
1
3
2
А) arcsin ; arcsin
; arcsin
2
2
2
3
2
1
Г ) arcsin
; arcsin
; arcsin
2
2
2
Верно
1
2
3
Б ) arcsin ; arcsin
; arcsin
2
2
2
Подумай!
2
1
3
Д ) arcsin
; arcsin ; arcsin
2
2
2
Подумай!
3
1
2
В) arcsin
; arcsin ; arcsin
2
2
2
Подумай!
Подумай!
2
3
1
Е ) arcsin
; arcsin
; arcsin
2
2
2
71.
Расположите числа3
2
arccos1; arccos
; arccos
2
2
в порядке возрастания.
Верно
3
2
А) arccos1; arccos
; arccos
2
2
3
2
Г ) arccos
; arccos
; arccos1
2
2
Подумай
2
3
Б ) arccos1; arccos
; arccos
2
2
Подумай!
2
3
Д ) arccos
; arccos1; arccos
2
2
Подумай!
3
2
В) arccos
; arccos1; arccos
2
2
Подумай!
Подумай!
2
3
Е ) arccos
; arccos
; arccos1
2
2
72.
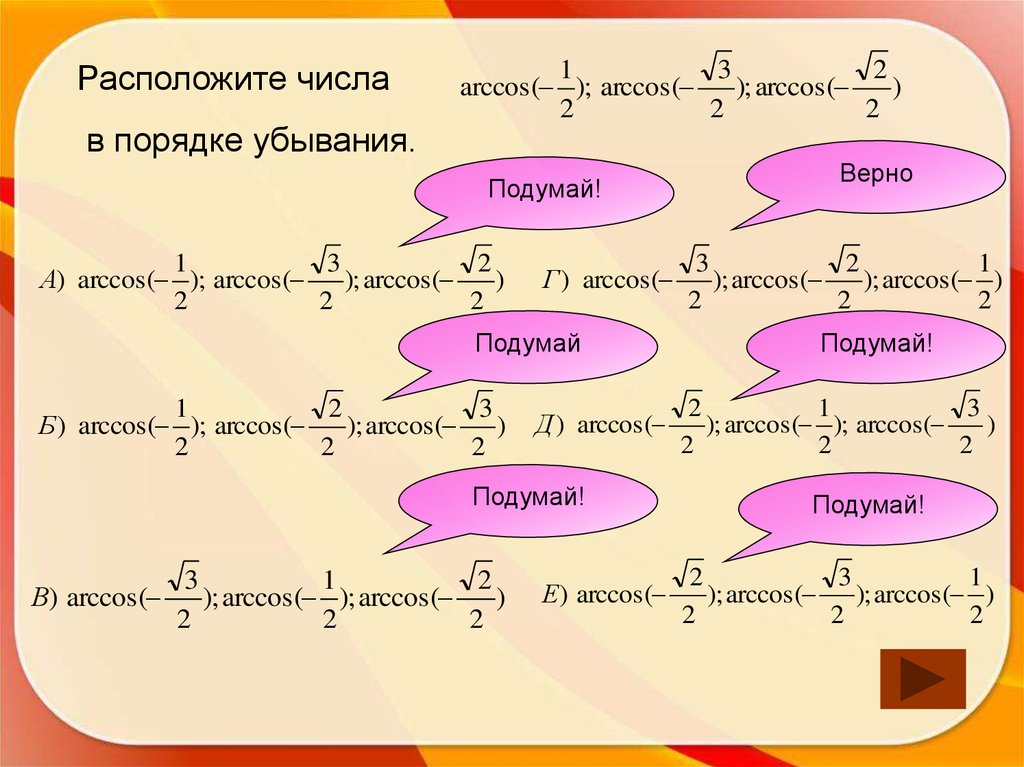
Расположите числав порядке убывания.
1
3
2
arccos( ); arccos(
); arccos(
)
2
2
2
Подумай!
1
3
2
А) arccos( ); arccos(
); arccos(
)
2
2
2
Г ) arccos(
Подумай
1
2
3
Б ) arccos( ); arccos(
); arccos(
)
2
2
2
Д ) arccos(
Подумай!
3
1
2
В) arccos(
); arccos( ); arccos(
)
2
2
2
Е ) arccos(
Верно
3
2
1
); arccos(
); arccos( )
2
2
2
Подумай!
2
1
3
); arccos( ); arccos(
)
2
2
2
Подумай!
2
3
1
); arccos(
); arccos( )
2
2
2
73.
Расположите числав порядке убывания.
1
2
arcsin( 1); arcsin( ); arcsin(
)
2
2
Подумай!
Подумай!
1
2
А) arcsin( ); arcsin( 1); arcsin(
)
2
2
Г ) arcsin( 1); arcsin(
Верно
1
2
Б ) arcsin( ); arcsin(
); arcsin( 1)
2
2
Д ) arcsin(
Подумай!
1
2
В) arcsin( 1); arcsin( ); arcsin(
)
2
2
Е ) arcsin(
2
1
); arcsin( )
2
2
Подумай!
2
1
); arcsin( ); arcsin( 1)
2
2
Подумай!
2
1
); arcsin( 1); arcsin( )
2
2
74.
Вы можете выйти изтренажера, начать заново или
перейти на главную страницу
Выберите нужное действие
Начать заново
Перейти на главную
Выход
75. МАТЕМАТИЧЕСКОЕ ЛОТО
Тема: «Решение простейшихтригонометрических уравнений»
76.
На каждом слайде нужно решить четыре уравнения ивыбрать правильный ответ.
В случае правильного ответа, откроется фрагмент
портрета известного ученого-математика.
НАЧАТЬ ИГРУ
77.
• Тригонометрические функции (получившие название отгреч. trigonon – треугольник и meteo – измеряю) играют
огромную роль в математике и ее приложениях.
• Исследованием тригонометрических функций практически
занимались ещё древнегреческие математики, изучая
взаимное изменение величин в геометрии и астрономии.
Соотношения между сторонами в прямоугольных
треугольниках, по своей сути являющиеся
тригонометрическими функциями, рассматривались уже в
III в. до н.э. в работах Евклида, Архимеда, Аполлония и
других ученых.
• Развитие теории тригонометрических функций было
продолжено в работах многих ученых.
78.
1cos x 1
2
sin 2 x 1
1)
3)
4
4
n, n Z
n
2
,n Z
2) 4 n, n Z
4) n, n Z
1) 2 n, n Z
2) 4 n, n Z
3) 2 n, n Z
4) n, n Z
1
cos x
0
2
2
sin x
0
2
1)
3)
4
4
2 n, n Z
n, n Z
2) ( 1) n
4)
4
4
n, n Z
2 n, n Z
1)
3)
3
3
2 n, n Z
n, n Z
2)
6
4)
2 n, n Z
3
2 n, n Z
79.
Кла́вдий Птолеме́й (ΚλαύδιοςΠτολεμαῖος, ок. 87—165) —
древнегреческий астроном,
математик, оптик, теоретик музыки и
географ.
•Ещё древнегреческие ученые
создали «тригонометрию хорд»,
выражавшую зависимости между
центральными углами круга и
хордами, на которые они опираются.
Этой тригонометрией пользовался во
II в. до н.э. в своих расчетах
древнегреческий астроном Гиппарх.
•Во II в. н.э. греческий ученый
Птоломей в своей работе «Алмагест»
(«Великая книга») также вывел
соотношения в круге, которые по
своей сути аналогичны
современным формулам синуса
половинного и двойного углов,
синуса суммы и разности двух углов.
80.
tgx2 cos x 3
1)
6
3) ( 1) n
2 n, n Z
3
2 n, n Z
2)
3
4) ( 1) n
2 n, n Z
6
n, n Z
1)
3)
3
2 n, n Z
3
3)
4
4
2 n, n Z
n, n Z
2)
4)
6
2)
n, n Z
tgx 1
1)
3
4)
n, n Z
6
n
2
,n Z
1
sin x 0
2
6
n, n Z
2 n, n Z
1) ( 1) n
3)
6
6
n, n Z
n, n Z
2)
6
2 n, n Z
4) ( 1) n
6
2 n, n Z
81.
• Франсуа Виет - выдающийсяфранцузский математик, один из
основоположников алгебры. По
образованию и основной
профессии — юрист
• Дополнил и систематизировал
различные случаи решения
плоских и сферических
треугольников, открыл "плоскую"
теорему косинусов и формулы для
тригонометрических функций от
кратных углов
Франсуа́ Вие́т
(фр. François Viète, seigneur de la
Bigotière; 1540—1603)
82.
Укажите наименьший положительныйкорень уравнения
sin(35 x)
1) 5
3)15
Укажите наименьший положительный
корень уравнения
tg (45 3 x)
2
2
1
3
2)110
1) 5
2) 55
4)10
3) 16 5
4) 45
Найдите сумму корней уравнения
cos2 x 2 cos x 3
на промежутке ( 5 ;8 )
Вычислите сумму корней уравнения
2 sin x tgx ctgx 0
на промежутке ( ; )
1) 12
2) 9
1)
2) 0
3) 4
4) 21
3) 2
4)
83.
Исаа́к Нью́то́н( 1643 — 1727)
Исаа́к Нью́ то́ н ( 1643 — 1727) —
английский физик, математик и астроном,
один из создателей классической физики.
Автор фундаментального труда
«Математические начала натуральной
философии», в котором он изложил закон
всемирного тяготения и три закона
механики, ставшие основой классической
механики. Разработал дифференциальное и
интегральное исчисление, теорию цвета и
многие другие математические и
физические теории.
Разложил тригонометрические функции в
ряды и открыл путь для их использования в
математическом анализе
84.
ctgx 32
cos x
2
1)
3
2 n, n Z
4
3) ( 1) n
4
n, n Z
2)
4
4) ( 1) n
2 n, n Z
3
n, n Z
4
1)
3)
3
n, n Z
2
n, n Z
3
tgx 1
1)
4
3)
2 n, n Z
4
n, n Z
2)
4
2)
4)
3
6
n, n Z
n, n Z
ctg x 0
n, n Z
3
4)
n, n Z
4
1)
2
3) ( 1) n
n, n Z
2
n, n Z
2) n, n Z
4) n, n Z
85.
Леонардо Эйлер - российский ишвейцарский математик, внёсший
значительный вклад в развитие
математики, а также механики,
физики, астрономии и ряда
прикладных наук.
Леонард Эйлер ввел и само
понятие функции и принятую в
наши дни символику.
Он придал всей тригонометрии
ее современный вид
Леона́рд Э́йлер
(нем. Leonhard Euler; 1707 — 1783)
86.
Вы можете выйти изтренажера, перейти на
главную страницу или начать
заново
Выберите нужное действие
Начать заново
Перейти на главную
Выход
















































 Математика
Математика