Единичная окружность в тригонометрии

1. «Единичная окружность в тригонометрии»

Элективный курс в форме уроков дистанционного обучения для учащихся 11 для
подготовки учащихся к решению задач повышенной сложности по теме «Тригонометрические уравнения и неравенства».
Работа выполнена учителем математики МОУ «Курлекская СОШ» Томского района Томской области
Логуновой Л.В.
Курлек - 2006

2. Зачем нужна единичная окружность?

Автоматический показ
Зачем нужна единичная окружность?
Единичная окружность
необходима при изучении
тригонометрических функций и
построении их графиков, часто
используется в решении
тригонометрических уравнений и
неравенств при отборе корней.
Цель: повторить, как
устанавливается соответствие
между действительными
числами на числовой прямой
и точками единичной
окружности; рассмотреть
использование единичной
окружность при решении
различных задач.
Рис.1

3. Содержание

Автоматический показ
Содержание
Урок 1 –
«Отображение точек числовой прямой на точки единичной окружности»
Урок 2 –
«Способ записи координаты точки единичной окружности»
Урок 3 – «Метод лепестков»
Урок 4 –
«Числовые промежутки на единичной окружности»
Урок 5 –
«Решение тригонометрических неравенств»
Итог

4. Урок 1

Определение
Способ задания соответствие ме
жду множеством действительных
чисел и точками единичной окру
жности
(криволинейная система координат)
Упражнения (тесты)
На содержание

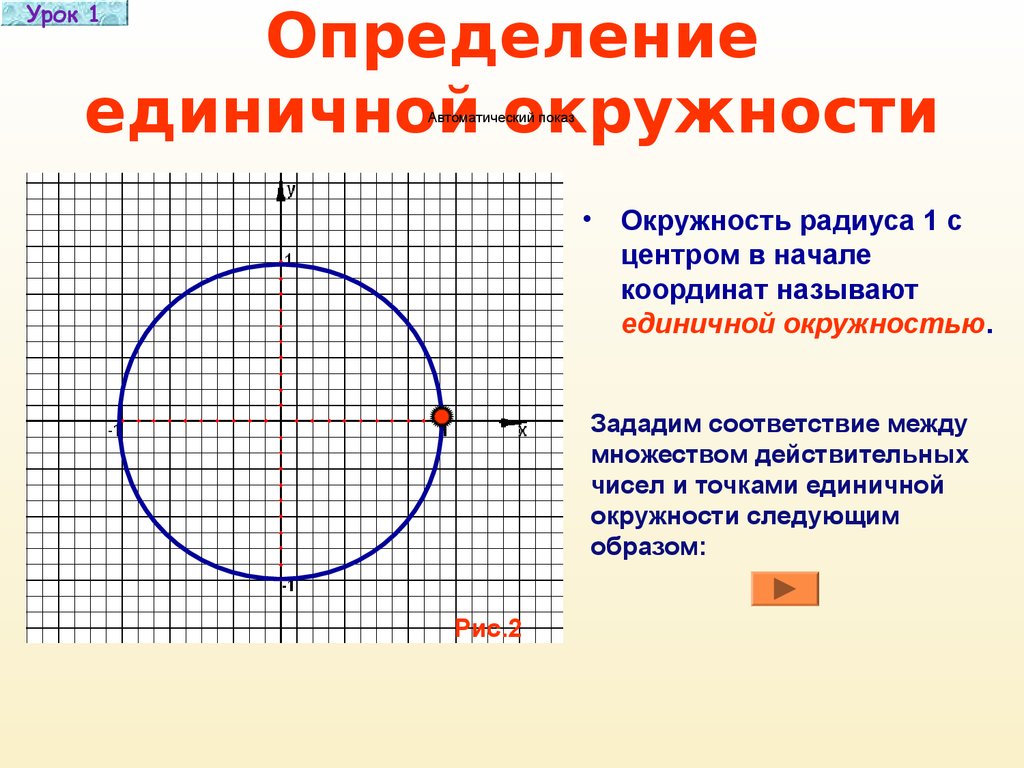
5. Определение единичной окружности

Урок 1
Определение
единичной окружности
Автоматический показ
Окружность радиуса 1 с
центром в начале
координат называют
единичной окружностью.
Зададим соответствие между
множеством действительных
чисел и точками единичной
окружности следующим
образом:
Рис.2

6. Способ задания соответствия между множеством действительных чисел и точками единичной окружности

Урок 1
Автоматический показ
Способ задания соответствия между множеством
действительных чисел и точками единичной окружности
Координатную прямую с началом отсчета в точке А будем
«наматывать», как нитку, на единичную окружность
сначала в положительном направлении – против хода
часовой стрелки,
потом в отрицательном – по ходу часовой стрелки.
4
4
4
4
Рис. 3
Вернуться

7.

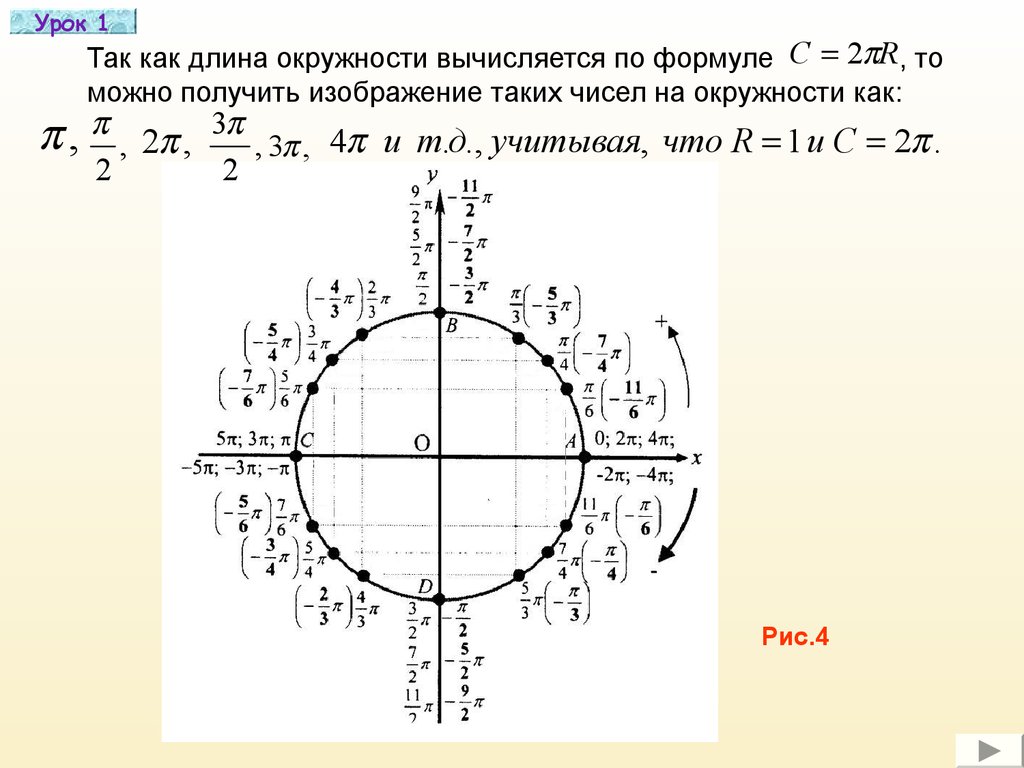
Урок 1
Так как длина окружности вычисляется по формуле С 2 R , то
можно получить изображение таких чисел на окружности как:
, , 2 ,
2
3
, 3 , 4 и т.д., учитывая, что R 1 и C 2 .
2
Рис.4

8.

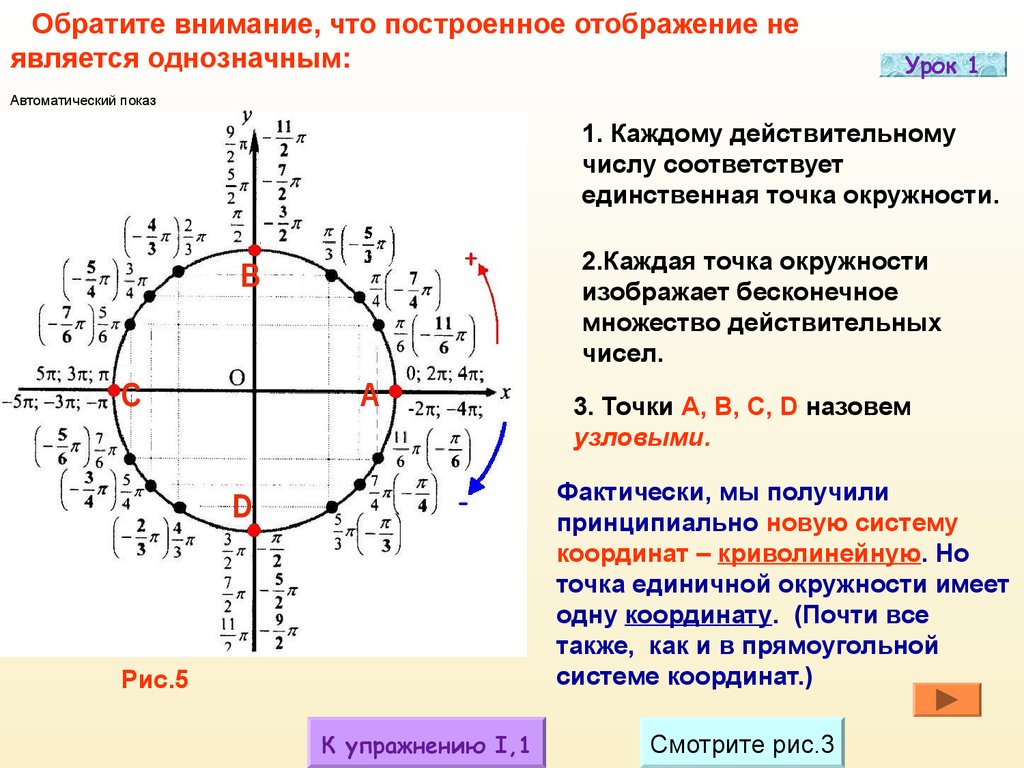
Обратите внимание, что построенное отображение не
является однозначным:
Урок 1
Автоматический показ
1. Каждому действительному
числу соответствует
единственная точка окружности.
2.Каждая точка окружности
изображает бесконечное
множество действительных
чисел.
В
С
А
3. Точки A, B, C, D назовем
узловыми.
Фактически, мы получили
принципиально новую систему
координат – криволинейную. Но
точка единичной окружности имеет
одну координату. (Почти все
также, как и в прямоугольной
системе координат.)
D
Рис.5
К упражнению I,1
Смотрите рис.3

9.

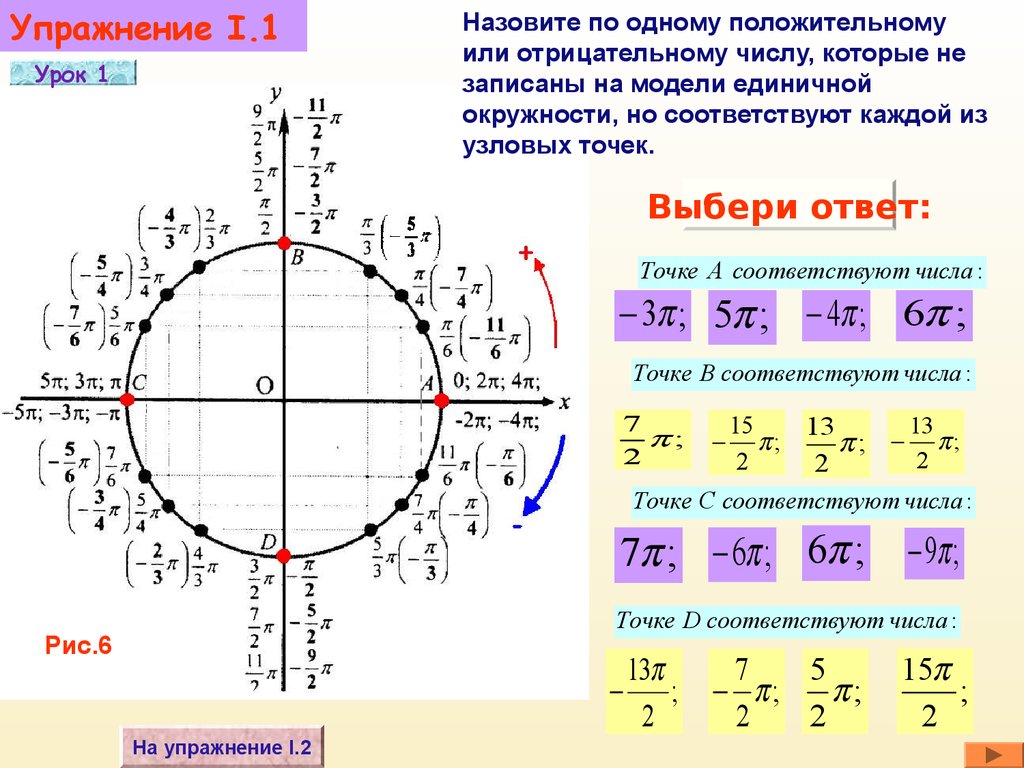
Упражнение I.1
Урок 1
Назовите по одному положительному
или отрицательному числу, которые не
записаны на модели единичной
окружности, но соответствуют каждой из
узловых точек.
Выбери ответ:
Точке А соответствуют числа :
3 ; 5 ; 4 ; 6 ;
Точке B соответствуют числа :
7
;
2
13
15
13
;
; ;
2
2
2
Точке С соответствуют числа :
7 ; 6 ; 6 ;
9 ;
Точке D соответствуют числа :
Рис.6
13
;
2
На упражнение I.2
7
5
;
;
2
2
15
;
2

10.

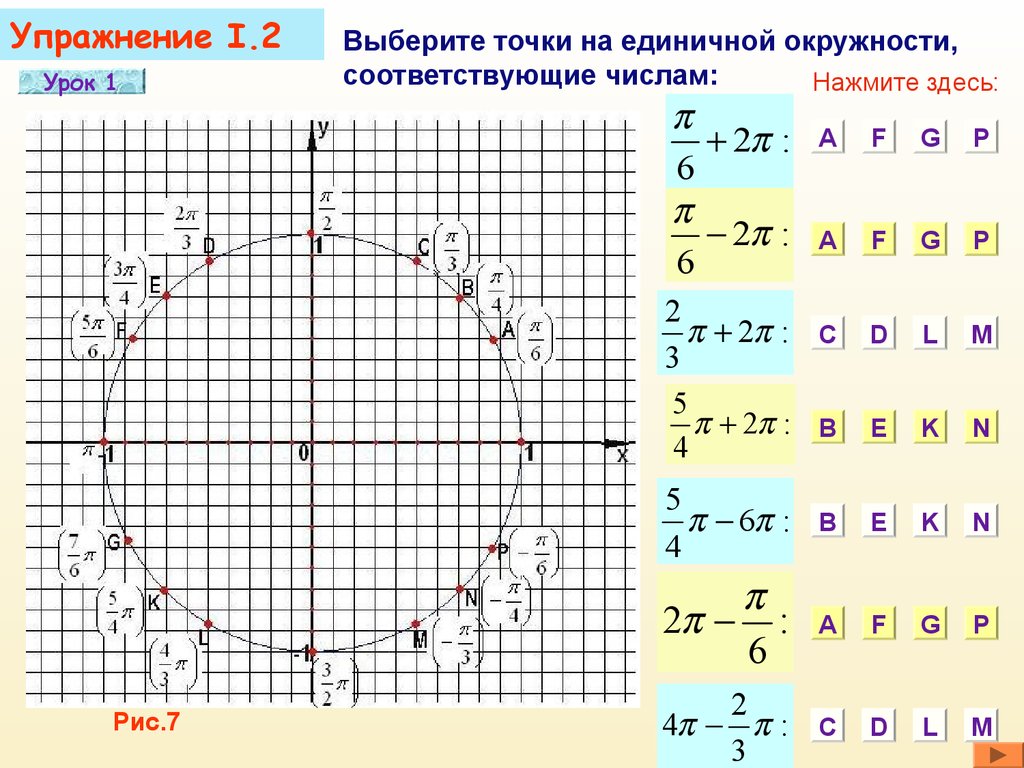
Упражнение I.2
Урок 1
Выберите точки на единичной окружности,
соответствующие числам:
Нажмите здесь:
2 :
6
2 :
6
A
F
G
P
A
F
G
P
C
D
L
M
5
2 : B
4
E
K
N
2
2 :
3
Рис.7
5
6 :
4
B
E
K
N
2 :
6
A
F
G
P
2
4 :
3
C
D
L
M

11. Урок 2

Способы записи чисел, соответс
твующих одной точке единичной
окружности
Упражнения:
II.1
II.2
На содержание

12.

Способы записи чисел, соответствующих
одной точке единичной окружности
Урок 2
Автоматический показ
Pt
Pt
На окружности дана произвольная
точка Pt , которая получается
поворотом точки P0 на угол t радиан
вокруг точки О.
При обходе окружности на целое число
оборотов мы попадаем в исходную точку, а
значит, точке окружности наравне с Pt
некоторым числом t соответствует и любое
число вида t 2 n, n Z
.
В данном случае точке Pt
соответствуют числа t 2 n, n Z.
К упражнению II.1

13.

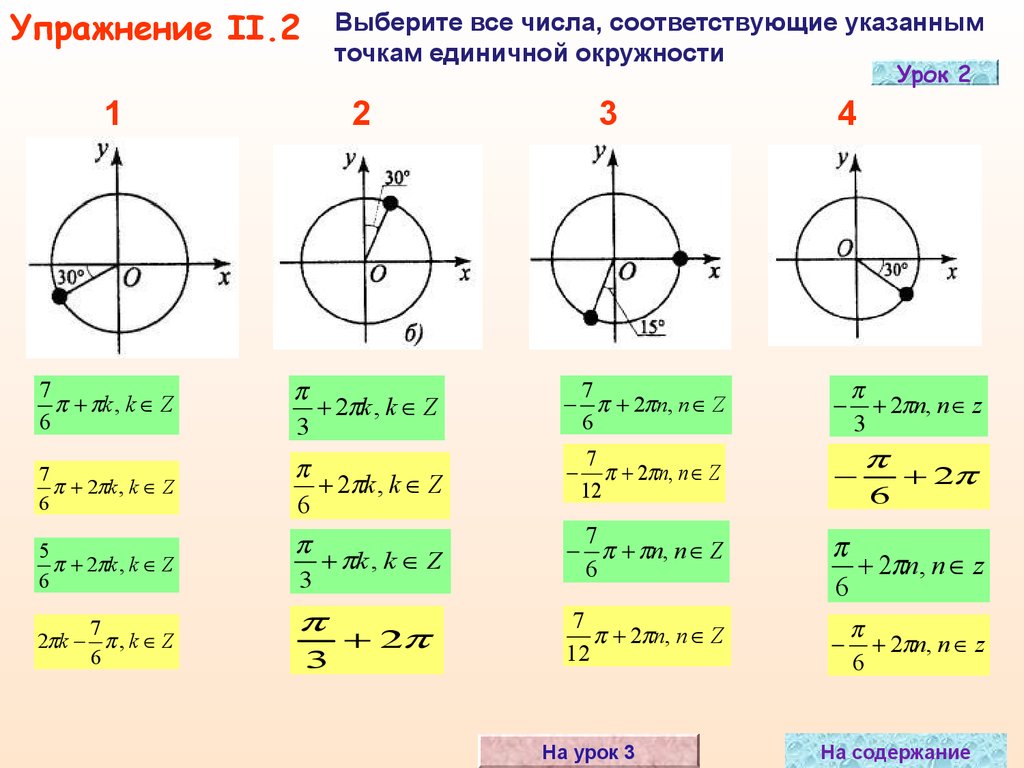
Упражнение II.1
1
Выберите все числа, соответствующие указанным
точкам единичной окружности
Урок 2
3
2
4
k , k Z
4
2 n, n Z
3
n, n Z
2
2 n, n Z
2 n, n Z
2
k , k Z
6
n, n Z
n, n Z
2
2 k , k Z
6
3
2 k , k Z
4
2 n , n Z
n, n Z
2
7
k , k Z
6
k , k Z
4
7
2 k , k Z
6
На упражнение II.2
2 k , k Z
4
На содержание

14.

Вернуться
к упражнению II.1

15.

Вернуться к
упражнению II.1

16.

Вернуться к
упражнению II.1

17.

Вернуться к
упражнению II.1

18.

Вернуться к
упражнению II.1
К упражнению II.2

19.

Упражнение II.2
Выберите все числа, соответствующие указанным
точкам единичной окружности
Урок 2
1
7
k , k Z
6
7
2 k , k Z
6
5
2 k , k Z
6
7
2 k , k Z
6
2
3
4
2 k , k Z
3
7
2 n, n Z
6
2 k , k Z
6
k , k Z
7
2 n, n Z
12
7
2 n, n Z
12
3
3
2
7
n, n Z
6
На урок 3
2 n, n z
3
6
2
2 n, n z
6
2 n, n z
6
На содержание

20.

На содержание
Вернуться к упражнению II.2

21.

Вернуться к упражнению II.2

22. Урок 3

Отбор чисел (Метод «лепестков»)
Пример1
Пример 2
Упражнения
На содержание

23. Отбор корней (Метод «лепестков»)

Отбор корней
Урок 3
лепестков»)
Автоматический показ
(Метод «
Решение многих тригонометрических уравнений приводит
к совокупности или системе их корней. Для грамотной
записи ответа, требующей, в частности, исключения
повторяющихся чисел, мы используем единичную
окружность.
Пример 1
Переписать данное условие так, чтобы в
них не было повторений.
Каждой серии чисел присваивается лепесток определенного
цвета:
m
x 4 , m Z
k
x , k Z
4 2
x 3 2 n, n Z
4

24.

Решение
Урок 3
Автоматический показ
m
x
, m Z
4
k
x , k Z
4 2
x 3 2 n, n Z
4
y
Теперь перенесем лепестки в нужные
места тригонометрической
окружности
Остается только записать числа,
соответствующие точкам, около
каждой из которых расположен хоть
один лепесток
Ответ:
О
х
l, l Z .
4

25.

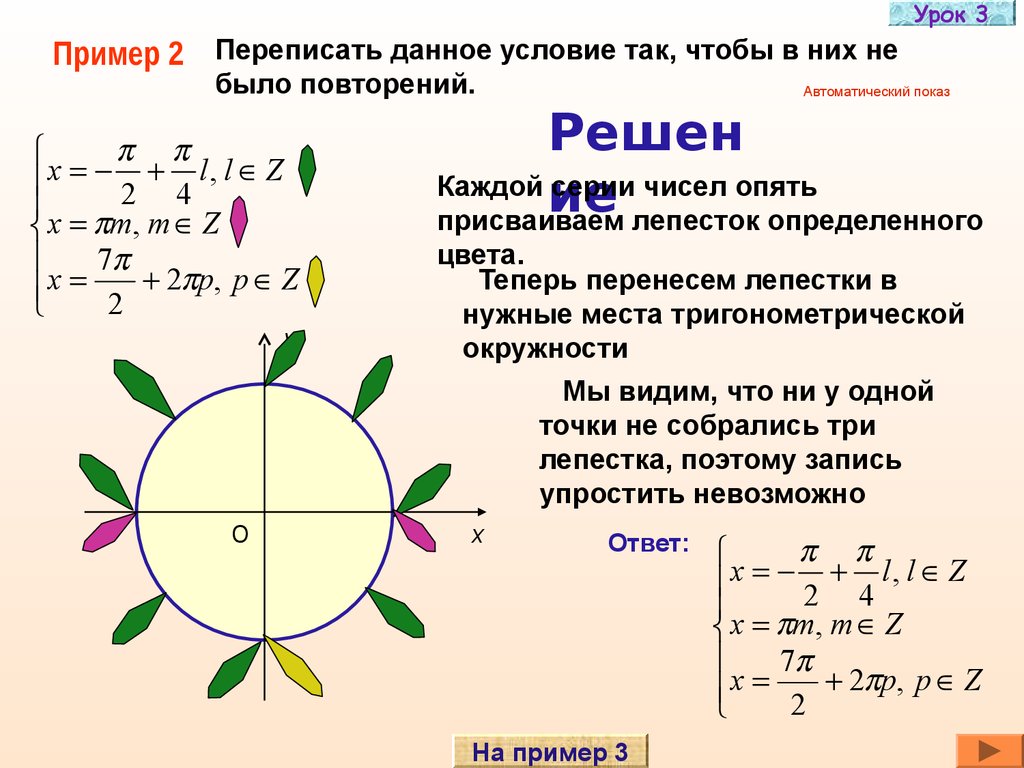
Урок 3
Пример 2 Переписать данное условие так, чтобы в них не
было повторений.
x
l, l Z
2 4
x m, m Z
7
x
2 p, p Z
2
y
О
Автоматический показ
Решен
Каждой серии чисел опять
ие
присваиваем лепесток определенного
цвета.
Теперь перенесем лепестки в
нужные места тригонометрической
окружности
Мы видим, что ни у одной
точки не собрались три
лепестка, поэтому запись
упростить невозможно
х
Ответ:
На пример 3
x 2 4 l, l Z
x m, m Z
7
x 2 2 p, p Z

26.

Пример 3
Запишите без повторений значения х, заданные следующими
условиями.
Урок 3
Решение
х
k , k Z
2
x t, t Z
2
Автоматический показ
Недопустимые точки на единичной окружности будем
отмечать крестиками, а точки вида
t, t Z
2
выделим светлыми лепестками.
y
Выражение
x
t, t Z
2
задает четыре точки единичной
окружности, из которых только две
допустимы.
О
х
Ответ:
x m, m Z .
На пример 4

27.

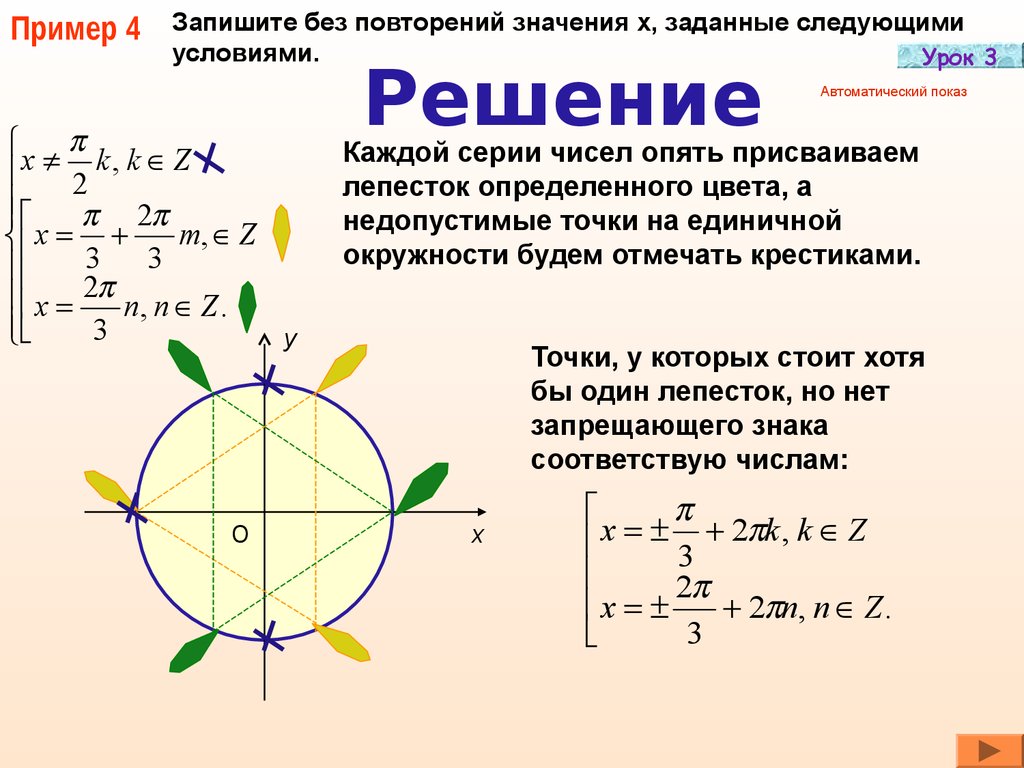
Пример 4
Запишите без повторений значения х, заданные следующими
условиями.
Урок 3
x
k, k Z
2
2
x
m, Z
3
3
x 2 n, n Z .
3
y
О
Решение
Автоматический показ
Каждой серии чисел опять присваиваем
лепесток определенного цвета, а
недопустимые точки на единичной
окружности будем отмечать крестиками.
Точки, у которых стоит хотя
бы один лепесток, но нет
запрещающего знака
соответствую числам:
х
x 3 2 k , k Z
2
x
2 n, n Z .
3

28.

Урок 3
Упражнения
Переписать данное условие так, чтобы в
них не было повторений в заданиях 1 и 2.
3)Выбрать наибольшее
отрицательное число.
4)Переписать данное
условие так, чтобы в них
не было повторений
m
x
, m Z
x 2 k , k Z
2
2 p
x 6 k
x
2 h, h Z
x 4 k
3) x
, p Z
2)
1)
6
5
4)
x 7 2 g , g Z
x 2 k : k Z x 2 k : k Z
6
x n, n Z .
4
6
2
k
x
, k Z
Выбери ответ: Выбери ответ:
Выбери ответ:
x k , k Z
2
x k , k Z
6
4
x , при p 1.
5
x k, k Z
4
x k, k Z
6
x
2
p, p Z
5
x
2 k , k Z
4
x
2 k , k Z
6
x
2
, при p 1.
5
x
k , k Z
4
x
5
k , k Z
6
x
2
p, p Z
2 5
На урок 4
6
3
Выбери ответ:
Нет решения
x p, p Z
x
m
2 m, m Z
2
x
5
k , k Z
6

29.

Упражнение I,1
Упражнение I,2

30.

Вернуться
к упражнению I,1
Вернуться
к упражнению I,2

31. Урок 4

Запись промежутков
Упражнения
На содержание

32.

Урок 4
Запись промежутков
Автоматический показ
Пример
Запиши все числа, соответствующие точкам выделенной дуги (или двух дуг)
на рисунке:
Решение
3
4
3
4
Ответ:
3
3
2
n
;
2
n
,
n
Z
4
4
Около одного из концов дуги записываем одно
из чисел, соответствующих этой точке.
Рисуем стрелку, направленную к другому концу
отмеченной дуги.
Стрелка снабжается знаком «+», если
движение направлено против хода часовой
стрелки, и знаком «-» минус, если оно идет по
ходу часовой стрелки.
Записываем соответствующее число около
второго конца дуги.
Записываем ответ с учетом, что каждой точке
единичной окружности соответствует
бесконечное множество действительных чисел.

33.

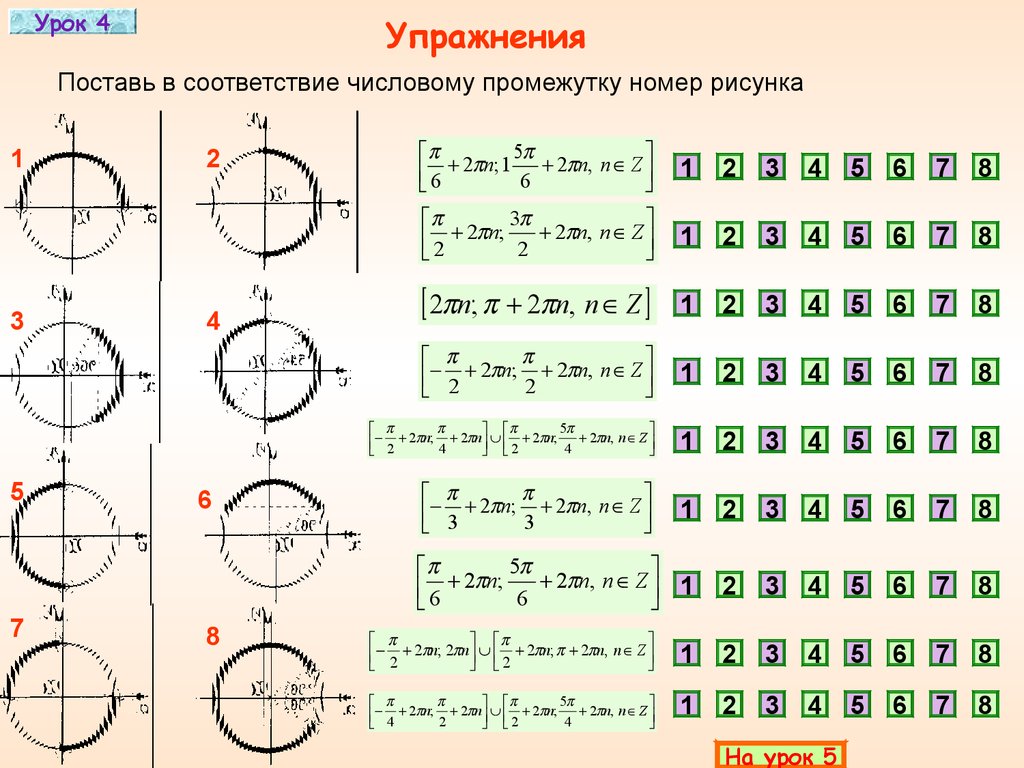
Урок 4
Упражнения
Поставь в соответствие числовому промежутку номер рисунка
1
3
5
7
2
4
6
8
5
2
n
;
1
2 n, n Z
6
6
1
2
3
4
5
6
7
8
3
2
n
;
2
n
,
n
Z
2
2
1
2
3
4
5
6
7
8
2 n; 2 n, n Z
1
2
3
4
5
6
7
8
2
n
;
2 n, n Z
2
2
1
2
3
4
5
6
7
8
5
2 2 n; 4 2 n 2 2 n; 4 2 n, n Z
1
2
3
4
5
6
7
8
2
n
;
2 n, n Z
3
3
1
2
3
4
5
6
7
8
5
2
n
;
2 n, n Z 1
6
6
2
3
4
5
6
7
8
2 2 n; 2 n 2 2 n; 2 n, n Z
1
2
3
4
5
6
7
8
5
4 2 n; 2 2 n 2 2 n; 4 2 n, n Z
1
2
3
4
5
6
7
8
На урок 5

34. Урок 5

Решение тригонометрических
неравенств (примеры)
Задание
На содержание

35.

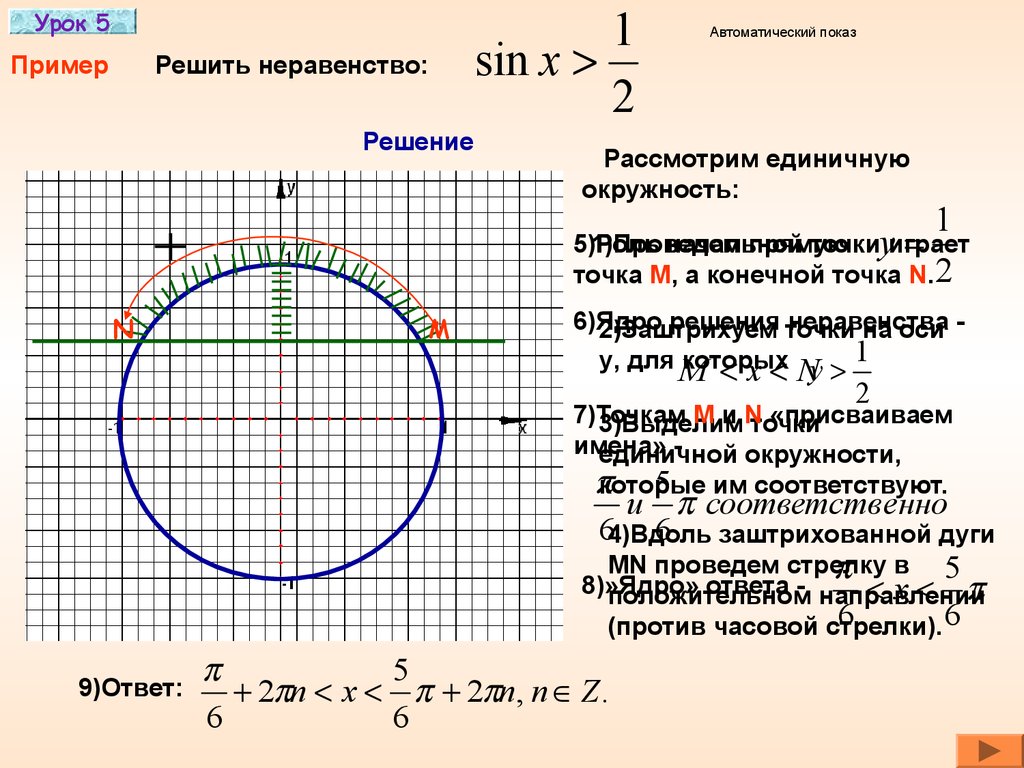
Урок 5
Пример
Решить неравенство:
Решение
Автоматический показ
Рассмотрим единичную
окружность:
1
5)Роль
1)Проведем
начальной
прямую
точкиyиграет
точка М, а конечной точка N. 2
N
1
sin x
2
M
6)Ядро
решения точки
неравенства
2)Заштрихуем
на оси 1
y, для M
которых
x Ny
2
7)Точкам
M и Nточки
«присваиваем
3)Выделим
имена»
единичной
окружности,
которые
5 им соответствуют.
и соответств енно
64)Вдоль
6 заштрихованной дуги
МN проведем стрелку
в 5
8)»Ядро»
ответа - направлении
x
положительном
6
6
(против часовой стрелки).
9)Ответ:
5
2 n x 2 n, n Z .
6
6

36.

Урок 5
Самостоятельная работа
Реши неравенство:
1)2 sin x 2 0
Ответ
3
2) cos x
2
Ответ
3)2 cos x 3 0
Ответ

37.

Урок 5
1)2 sin x 2 0
Ответ:
5
2 n x 2 n, n Z .
4
4
К самостоятельной работе

38.

Урок 5
3
2) cos x
2
Ответ:
2 n x 2 n, n Z .
6
6
К самостоятельной работе

39.

Урок 5
3)2 cos x 3 0
Ответ:
11
2 n x
2 n, n Z .
6
6
К самостоятельной работе
На итог

40. Подведем итог

Теперь ты можешь приступать к решению заданий
повышенной сложности по тригонометрии, то есть к
решению тригонометрических уравнений и задач. Ведь ты
теперь знаешь и умеешь
Смотри

41. Содержание

Урок 1 –
«Отображение точек числовой прямой на точки единичной окружности»
Урок 2 –
«Способ записи координаты точки единичной окружности»
Урок 3 – «Метод лепестков»
Урок 4 –
«Числовые промежутки на единичной окружности»
Урок 5 –
«Решение тригонометрических неравенств»
Смотри список литературы и
других ресурсов

42. Литература и другие ресурсы для самостоятельной работы

Практикум по элементарной математике.
Тригонометрия. Авторы – В.Н. Литвиненко, А.Г.
Мордкович, Москва, «Вербум – М», 2000.
Лев Великович "Лоцман абитуриента в океане
математики" http://www.trizway.com/show.php?id=63&pg=1#a1
(Подключись к Интернету, скопируй эту ссылку в адресную строку в обозревателе и нажми
«Enter» ).
Сайт элементарной математики Дмитрия Гущина
http://mathnet.spb.ru/
(Подключись к Интернету, скопируй эту ссылку в адресную строку в обозревателе и нажми
«Enter» ).
Не упускай своих возможностей!
Твой
На содержание
учител