Подготовка к ЕГЭ. Об особенностях решения заданий С2 ЕГЭ

1.

Подготовка к ЕГЭ
Об особенностях решения заданий
С2 ЕГЭ
1
Е.Ю.Фролова, учитель математики ГБОУ СОШ №2 г.о. Кинель

2.

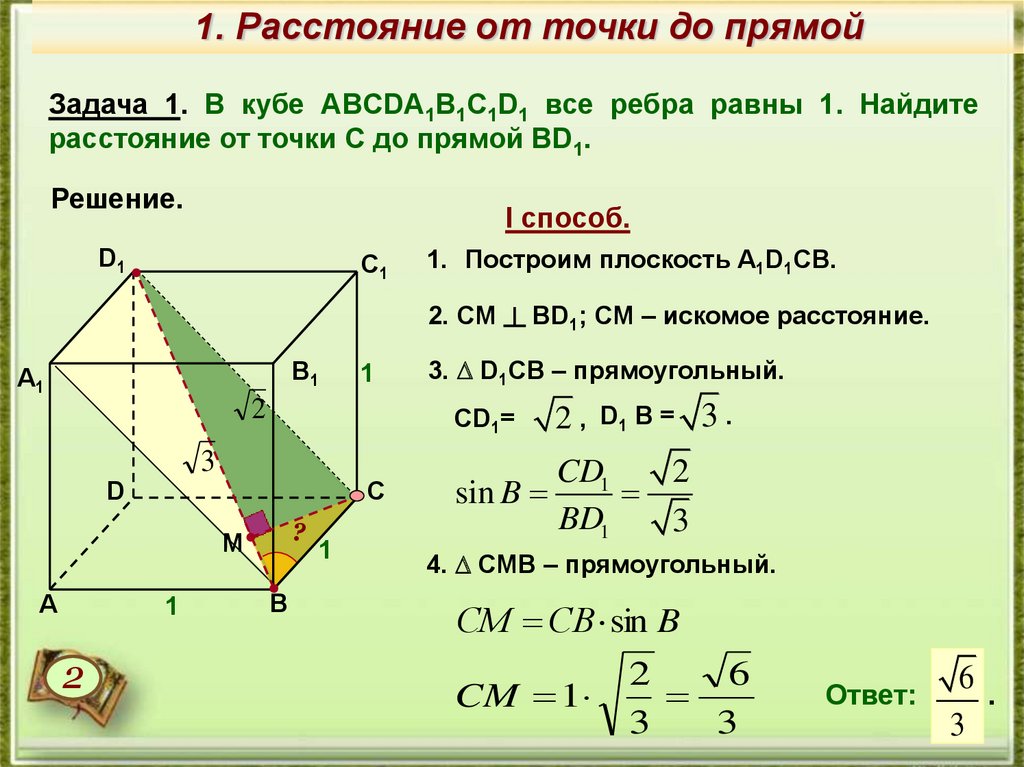
1. Расстояние от точки до прямой
Задача 1. В кубе ABCDA1B1C1D1 все ребра равны 1. Найдите
расстояние от точки С до прямой BD1.
Решение.
I способ.
D1
C1
1. Построим плоскость A1D1СВ.
2. СМ ┴ BD1; СМ – искомое расстояние.
B1
А1
1
2
CD1=
3
C
D
?
М
А
1
2
3. D1CB – прямоугольный.
B
1
2,
D1 В =
3.
CD1
2
sin B
BD1
3
4. CMB – прямоугольный.
СМ СВ sin B
CM 1
2
6
3
3
Ответ:
6.
3

3.

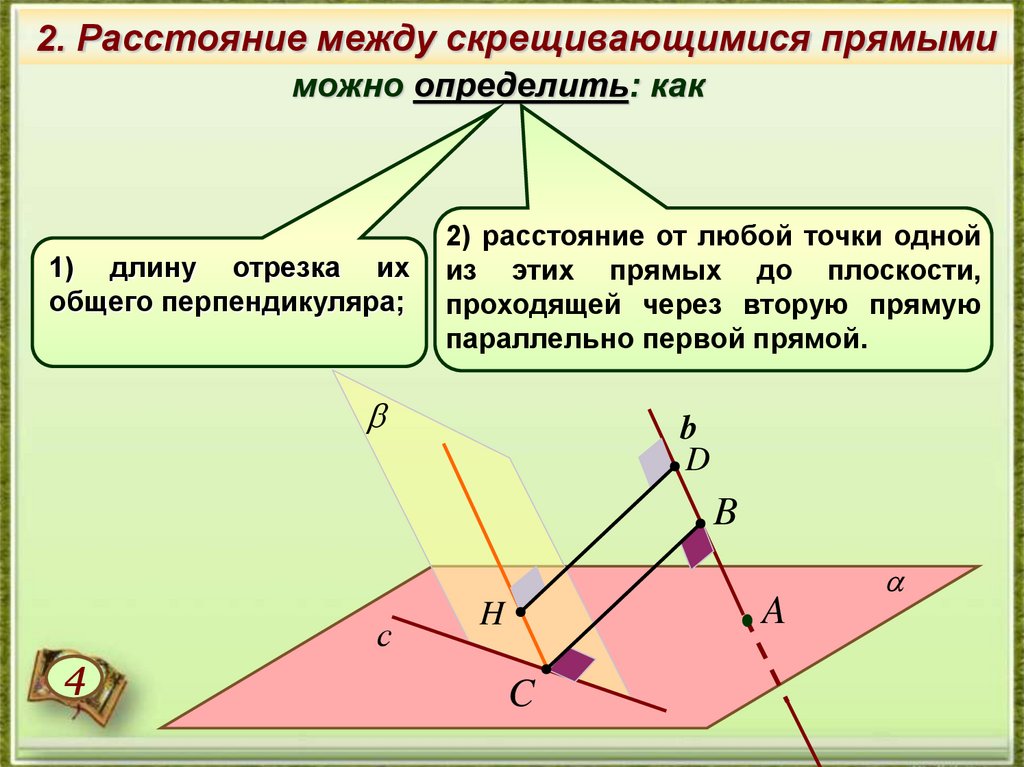
2. Расстояние между скрещивающимися прямыми
можно определить: как
1) длину отрезка их
общего перпендикуляра;
2) расстояние от любой точки одной
из этих прямых до плоскости,
проходящей через вторую прямую
параллельно первой прямой.
b
D
B
4
с
A
H
C

4.

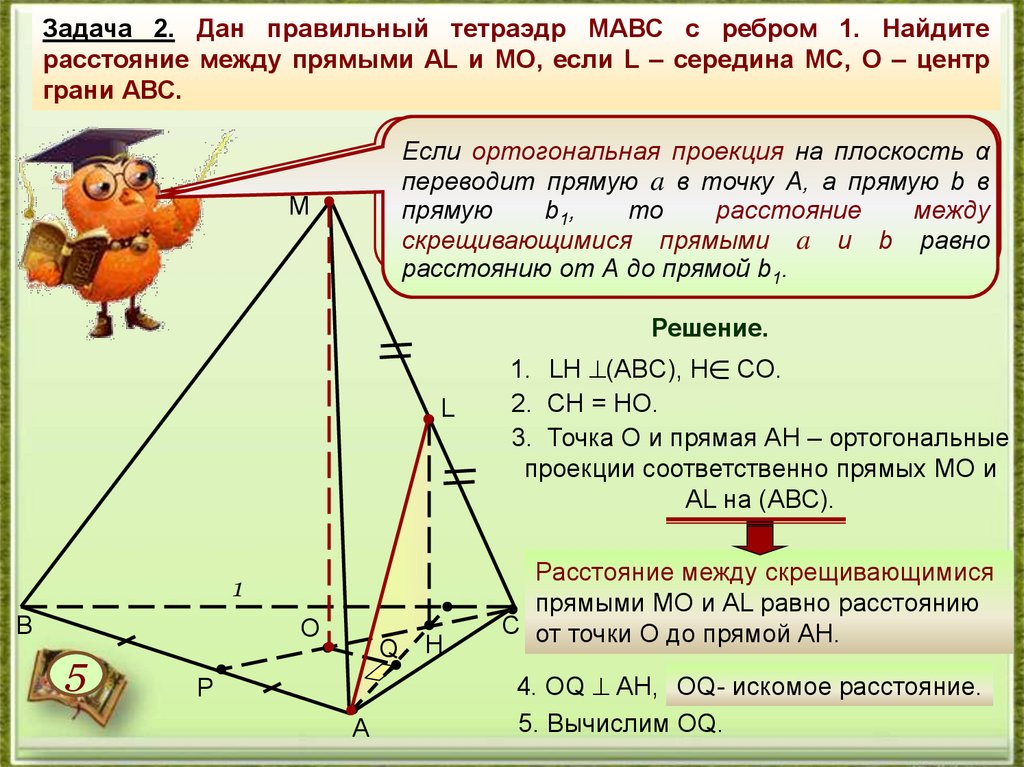
Задача 2. Дан правильный тетраэдр МАВС с ребром 1. Найдите
расстояние между прямыми АL и МО, если L – середина МС, О – центр
грани АВС.
Расстояние
между скрещивающимися
прямымиα
Если ортогональная
проекция на плоскость
равно
расстоянию
одной bизв
переводит
прямуюот
a влюбой
точку точки
A, а прямую
прямую
, плоскости,
то
расстояние
этих
прямыхb1до
проходящей между
через
скрещивающимися
прямыми
a ипрямой.
b равно
вторую
прямую параллельно
первой
расстоянию от А до прямой b1.
M
Решение.
L
1
В
О
5
Q
Р
А
Н
1. LН (ABC), Н СО.
2. СН = НО.
3. Точка О и прямая АН – ортогональные
проекции соответственно прямых МО и
АL на (АВС).
Расстояние между скрещивающимися
прямыми МО и АL равно расстоянию
С от точки О до прямой АН.
4. ОQ АН, ОQ- искомое расстояние.
5. Вычислим ОQ.

5.

M
AP
AHP : sin AHP
AH
Решение.
1
О
Q Н
Р
OQ
7 .
Ответ:
14
О ?
В
7
14
H
Q
OQ
OQH : sin OHQ
OQ OH sin OQH
OH
.
ОQ
OH AP
AP 2 PH 2
2
3
CP
2
3
ОН
6
3
РН
3
С
С
А
6
AP PH
2
1
OH CP
3
2
PH CP
3
CP AC sin 60
L
В
AP
1
К
60◦
Р
1
2
А

6.

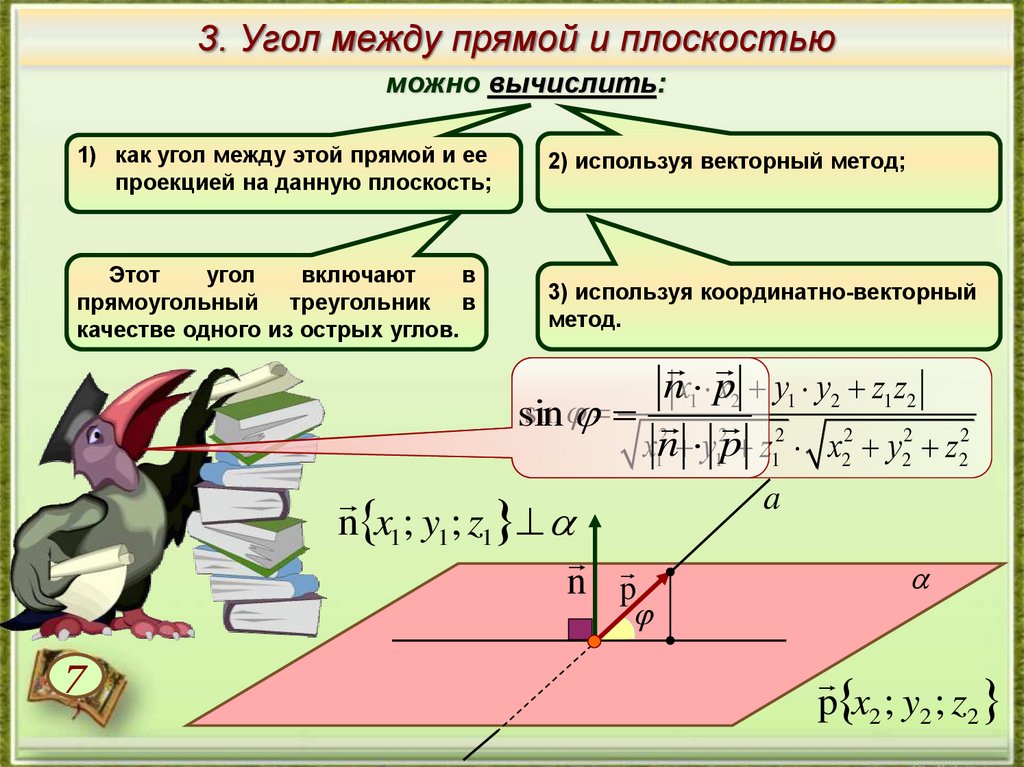
3. Угол между прямой и плоскостью
можно вычислить:
1) как угол между этой прямой и ее
проекцией на данную плоскость;
2) используя векторный метод;
Этот
угол
включают
в
прямоугольный треугольник в
качестве одного из острых углов.
3) используя координатно-векторный
метод.
nх1 pх2 у1 у2 z1 z2
sin
sin
2
х1n
у12p z12 х22 у22 z22
n x1; y1; z1
n p
7
a
p x2 ; y2 ; z2

7.

Задача 3. В правильной четырехугольной пирамиде SАВСD, все ребра
которой равны 1. Найдите угол между прямой DЕ, где Е - середина
апофемы SF грани АSВ, и плоскостью АSC.
S
Решение.
Е
В
С
F
8
D
А

8.

S
I способ.
1) ОD (АSC).
4)
1
ОD (а в )
2
5)
DE DA AF FE
OD – вектор нормали к (АSС).
2) DE – направляющий
вектор прямой DE.
3) Пусть
АD а
с
АВ в
АS c
Е
С
В
О
F
D
9
а
А
1
1
1
1
1
DE а в (с в ) а в с
2
2
2
4
2
в

9.

1
1
1
DE
OD
ОD (а в )
DE a b c
sin
2
4
2
DE ОD
2 2
а а
1 1
1 1
1 2 1 2 1
1
DE ОD ( а в с ) ( а в ) а в ас вс
4 2
2 2
2
8
4
4
5
DE ОD
8
2 1 1 2
15
DE DE a b c
4 2
4
2
10
ОD
2
5
sin
30
30
Ответ: arcsin
.
6

10.

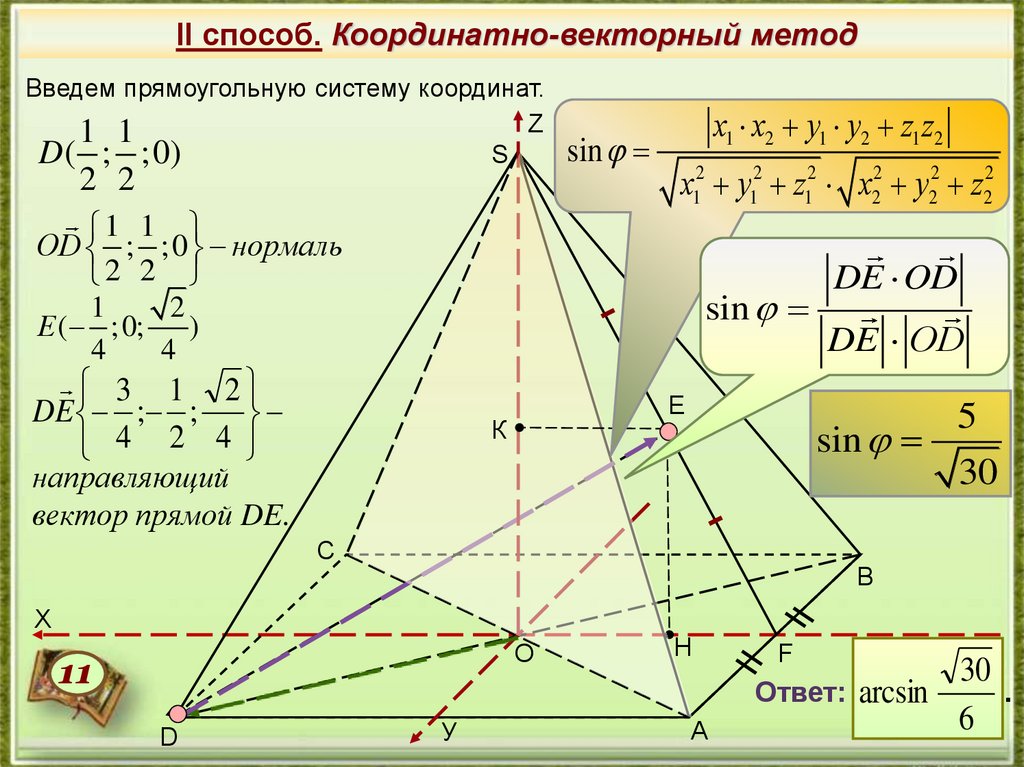
II способ. Координатно-векторный метод
Введем прямоугольную систему координат.
Z
1 1
D ( ; ;0)
S
2 2
1 1
ОD ; ;0 нормаль
2 2
1
2
Е ( ;0;
)
4
4
sin
х1 х2 у1 у2 z1 z2
х12 у12 z12 х22 у22 z22
sin
3 1 2
DE ; ;
4 2 4
Е
К
DE ОD
5
sin
30
направляющий
вектор прямой DE.
С
В
Х
О
11
D
DE OD
У
Н
А
F
30
Ответ: arcsin
.
6

11.

4. Угол между пересекающимися плоскостями
можно вычислить: как
1) угол между прямыми, лежащими в
этих плоскостях и перпендикулярными
к линии их пересечения;
2) угол между перпендикулярными
им прямыми.
Линейный угол двугранного
угла, если удается, включают в
некоторый треугольник.
М
D
12
а
А
О

12.

Задача 4. Основание прямой четырехугольной призмы прямоугольник
АВСD, в котором АВ=5, АD=√33. Найдите тангенс угла между плоскостью
грани АА1D1D призмы и плоскостью, проходящей через середину ребра
СD, перпендикулярно прямой В1D, если расстояние между прямыми А1С1 и
ВD равно√3.
Решение.
D1
С1
В1
A1
Пусть β - плоскость,
проходящая
через середину
По теореме
Пифагора
найдем
ребра СD
2 перпендикулярно
2
ВС
ВВ
В1С=прямой В1D.
1 6
Угол между данными
плоскостями - угол между
перпендикулярными к ним
прямыми.
3
D
С
33
А
5
13
СD┴(AA1D)
В1D ┴ β – по условию
В
В1С 6
tg В1DC
DC 5
В1DC
– ИСКОМЫЙ.

13.

Подготовка к ЕГЭ
17
Е.Ю.Фролова, учитель математики ГБОУ СОШ №2 г.о. Кинель