Решение метрических задач. Лекция 3

1. Лекция 3. Решение метрических задач

1. Метрические задачи.
2. Определение натуральной величины отрезка и
углов наклона к плоскостям проекций методом
прямоугольного треугольника.
3. Решение
метрических
задач
методами
преобразования проекций.
Положения геометрических образов, при которых
расстояния и углы не искажаются на плоскостях проекций.
4 основных задачи преобразования проекций.
Решение 1-ой и 2-ой задачи преобразования проекций
методом вращения, плоскопараллельного перемещения и
замены плоскостей проекций.
Решение 3-ой и 4-ой задачи преобразования проекций
методом плоскопараллельного перемещения и замены
плоскостей проекций.

2. 1. Метрические задачи

К метрическим задачам относятся задачи на
определение натуральной величины отрезков,
расстояний углов, площадей плоских фигур

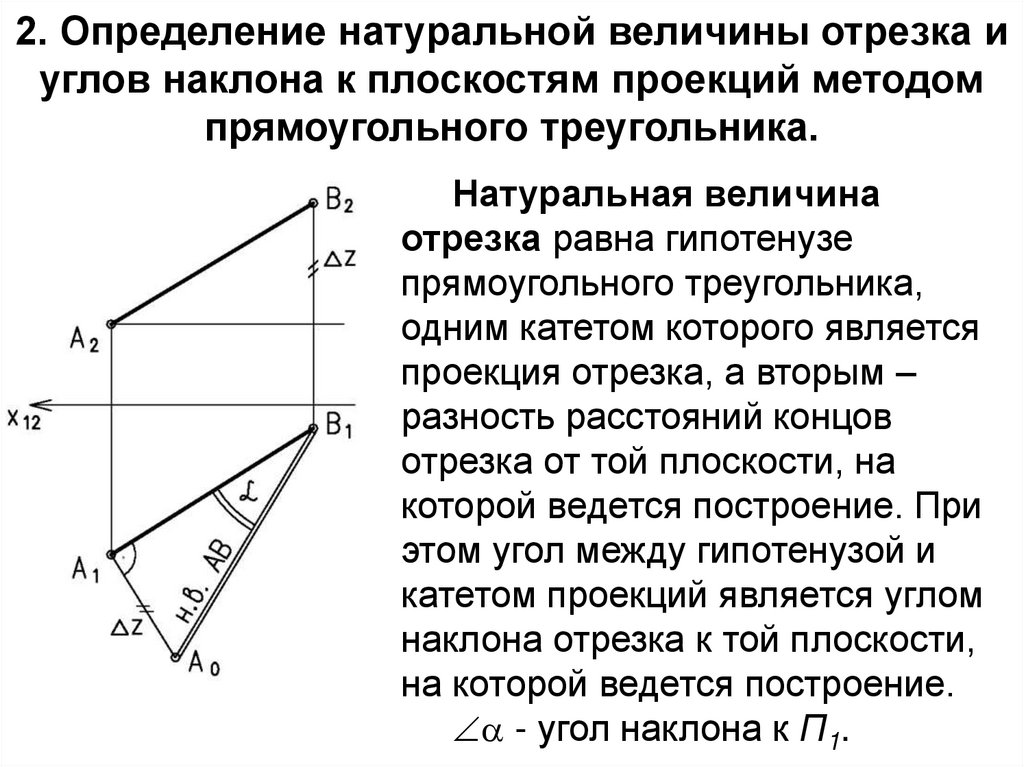
3. 2. Определение натуральной величины отрезка и углов наклона к плоскостям проекций методом прямоугольного треугольника.

Натуральная величина
отрезка равна гипотенузе
прямоугольного треугольника,
одним катетом которого является
проекция отрезка, а вторым –
разность расстояний концов
отрезка от той плоскости, на
которой ведется построение. При
этом угол между гипотенузой и
катетом проекций является углом
наклона отрезка к той плоскости,
на которой ведется построение.
- угол наклона к П1.

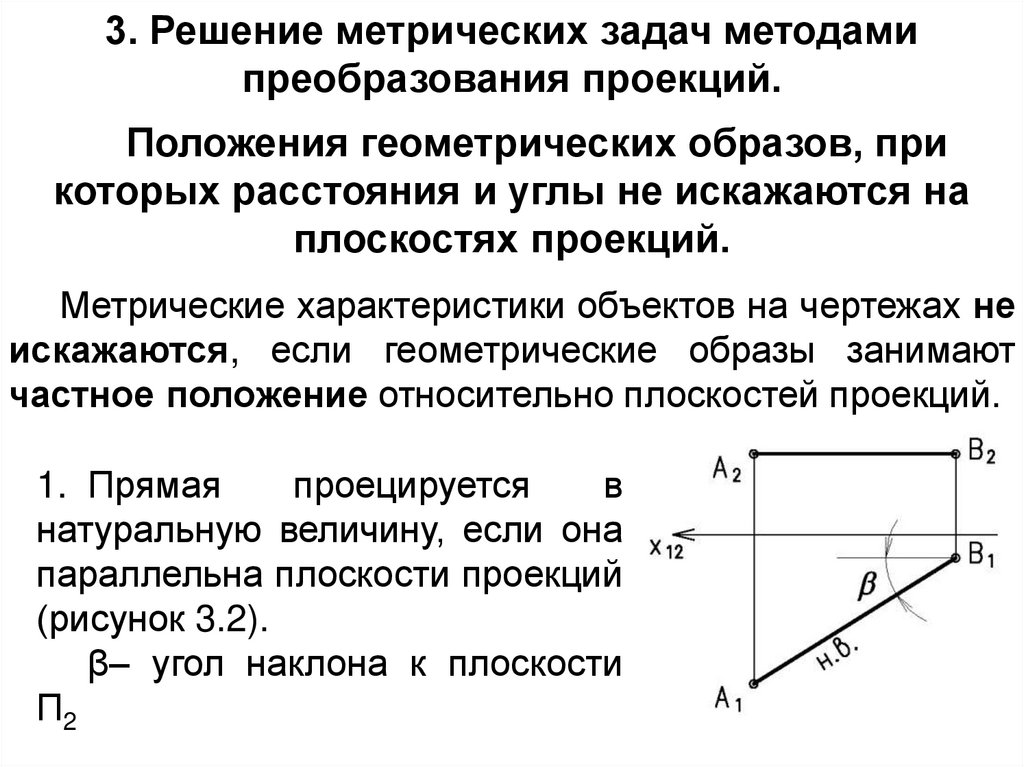
4. 3. Решение метрических задач методами преобразования проекций.

Положения геометрических образов, при
которых расстояния и углы не искажаются на
плоскостях проекций.
Метрические характеристики объектов на чертежах не
искажаются, если геометрические образы занимают
частное положение относительно плоскостей проекций.
1. Прямая
проецируется
в
натуральную величину, если она
параллельна плоскости проекций
(рисунок 3.2).
β– угол наклона к плоскости
П2

5.

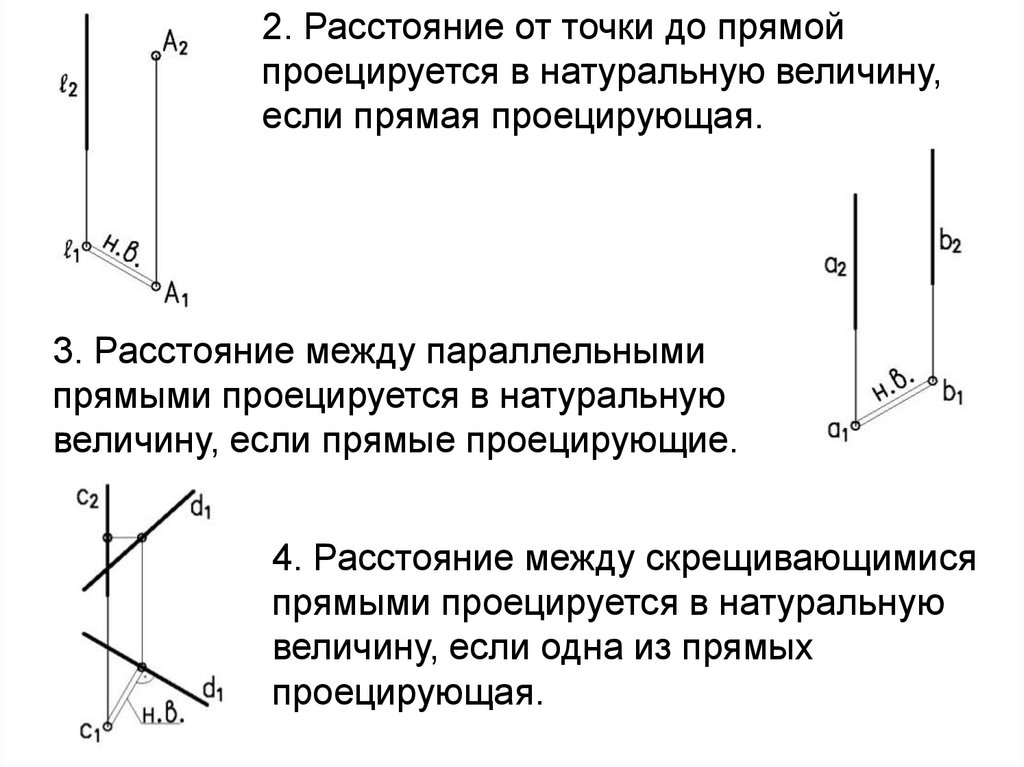
2. Расстояние от точки до прямой
проецируется в натуральную величину,
если прямая проецирующая.
3. Расстояние между параллельными
прямыми проецируется в натуральную
величину, если прямые проецирующие.
4. Расстояние между скрещивающимися
прямыми проецируется в натуральную
величину, если одна из прямых
проецирующая.

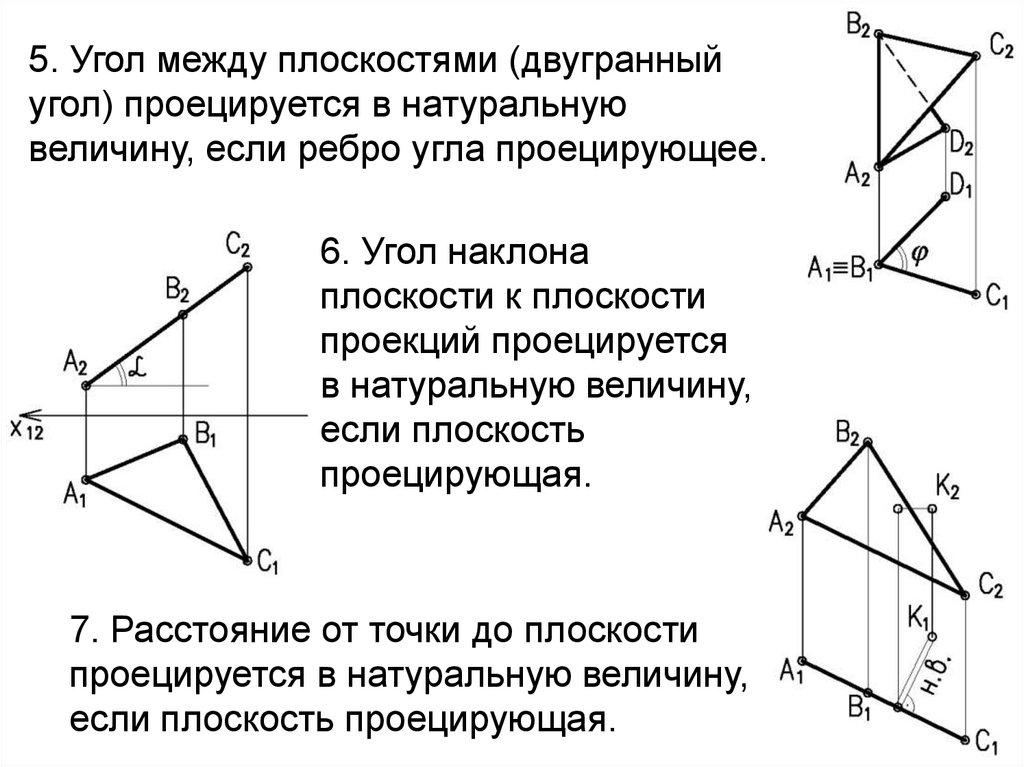
6. 5. Угол между плоскостями (двугранный угол) проецируется в натуральную величину, если ребро угла проецирующее.

6. Угол наклона
плоскости к плоскости
проекций проецируется
в натуральную величину,
если плоскость
проецирующая.
7. Расстояние от точки до плоскости
проецируется в натуральную величину,
если плоскость проецирующая.

7.

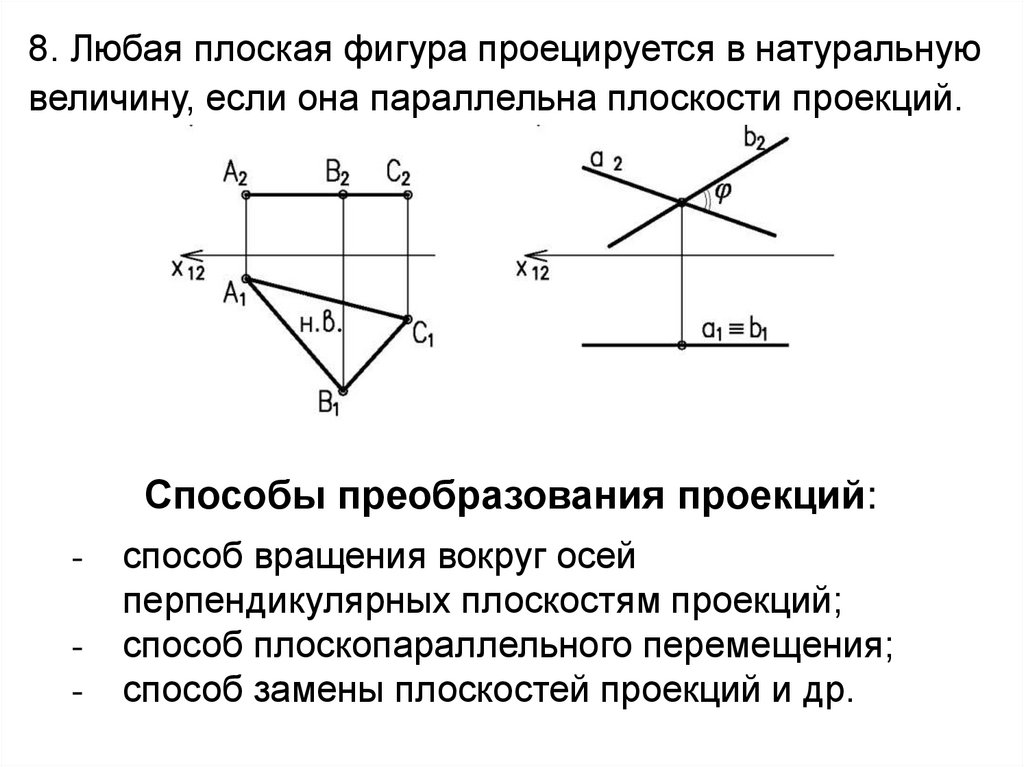
8. Любая плоская фигура проецируется в натуральную
величину, если она параллельна плоскости проекций.
Способы преобразования проекций:
-
-
способ вращения вокруг осей
перпендикулярных плоскостям проекций;
способ плоскопараллельного перемещения;
способ замены плоскостей проекций и др.

8. 4 основных задачи преобразования проекций.

Задача 1. Прямую общего положения преобразуем в
линию уровня (одно преобразование).
Задача 2. Прямую общего положения преобразуем в
проецирующую (два преобразования).
Задача
3.
преобразования
преобразование).
Плоскость
общего
положения
в
проецирующую
(одно
Задача 4. Плоскость общего положения преобразуем
в плоскость уровня (два преобразования).

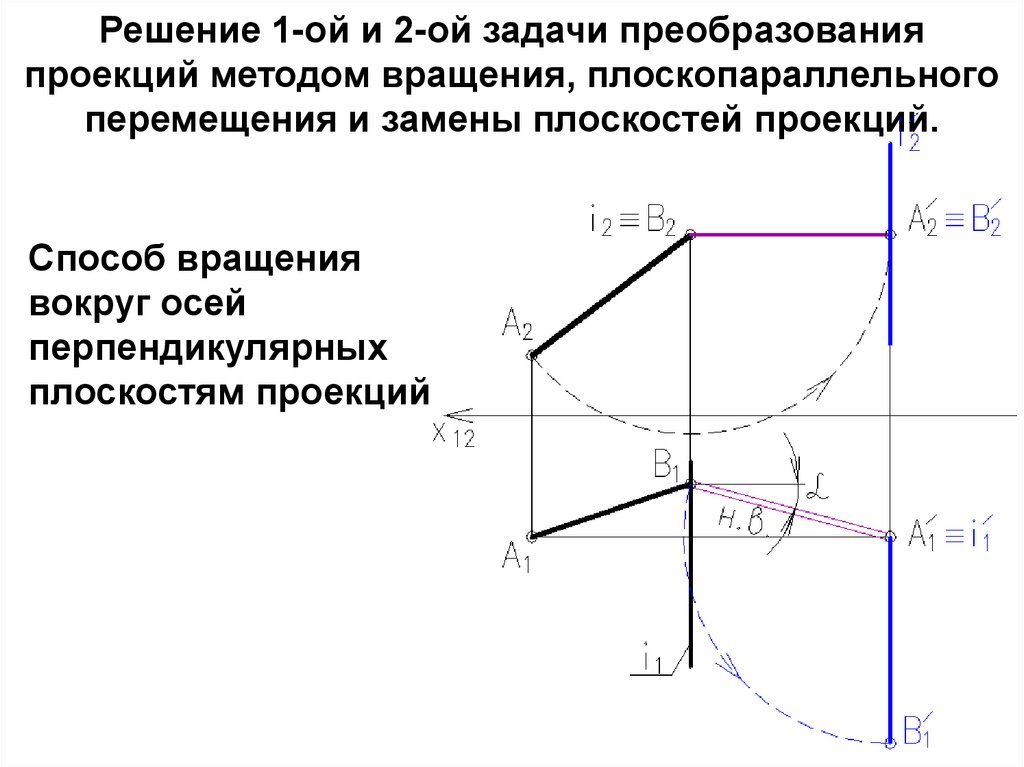
9. Решение 1-ой и 2-ой задачи преобразования проекций методом вращения, плоскопараллельного перемещения и замены плоскостей

проекций.
Способ вращения
вокруг осей
перпендикулярных
плоскостям проекций

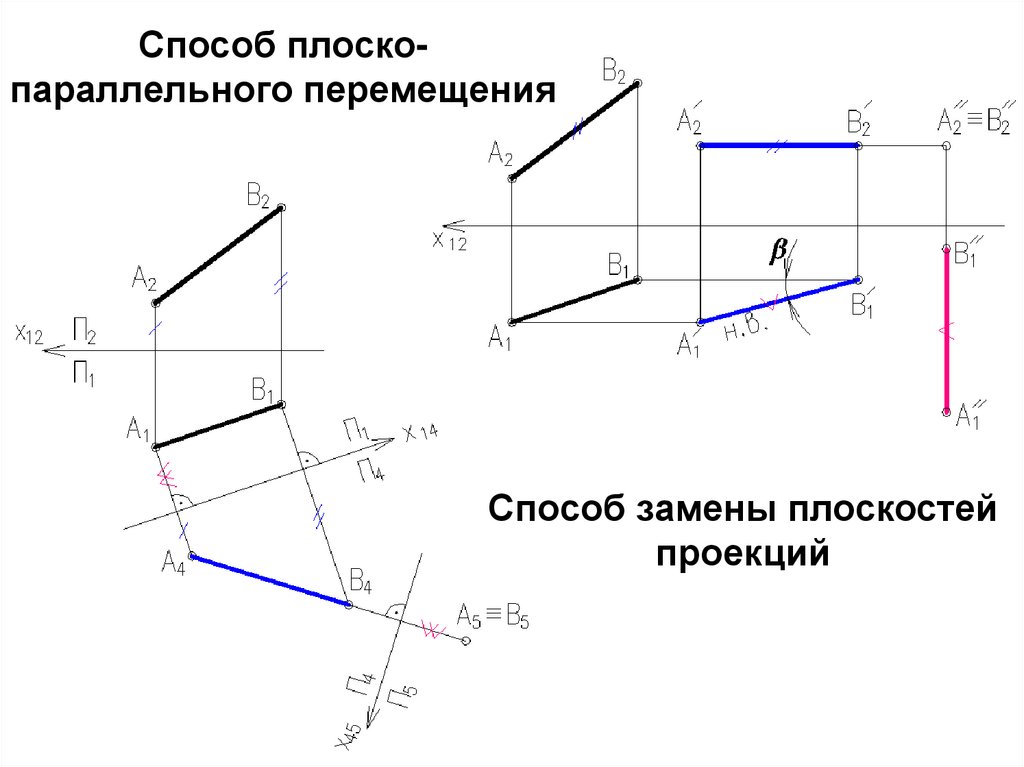
10. Способ плоско-параллельного перемещения

Способ плоскопараллельного перемещения
Способ замены плоскостей
проекций

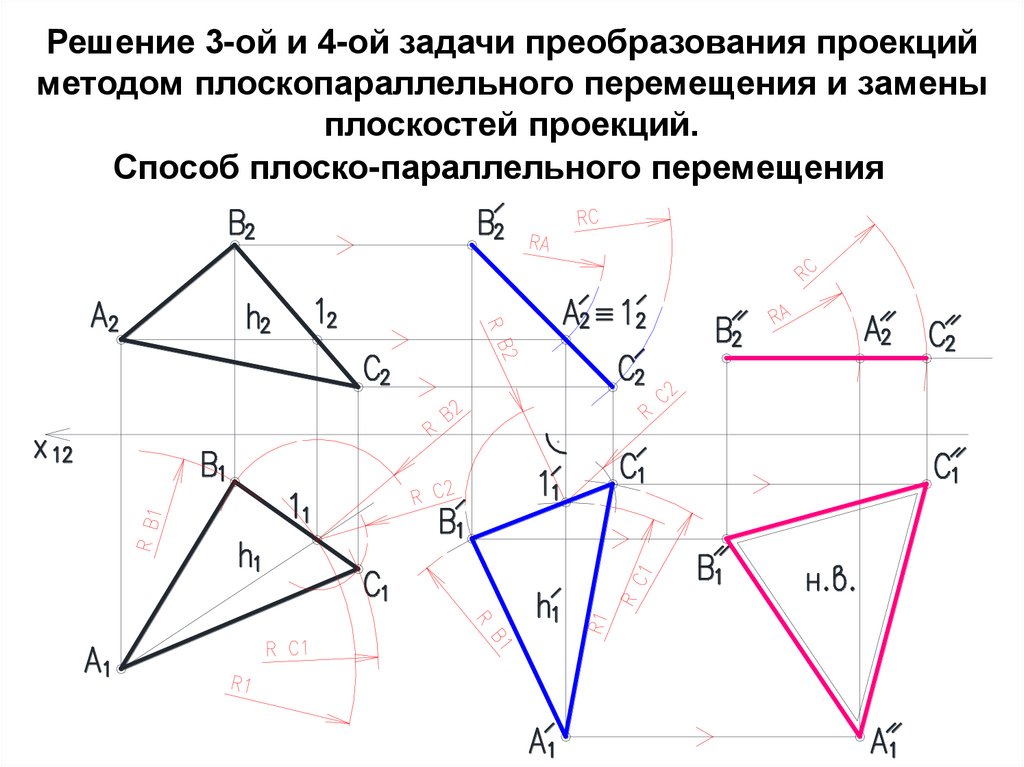
11. Решение 3-ой и 4-ой задачи преобразования проекций методом плоскопараллельного перемещения и замены плоскостей проекций.

Способ плоско-параллельного перемещения

12.

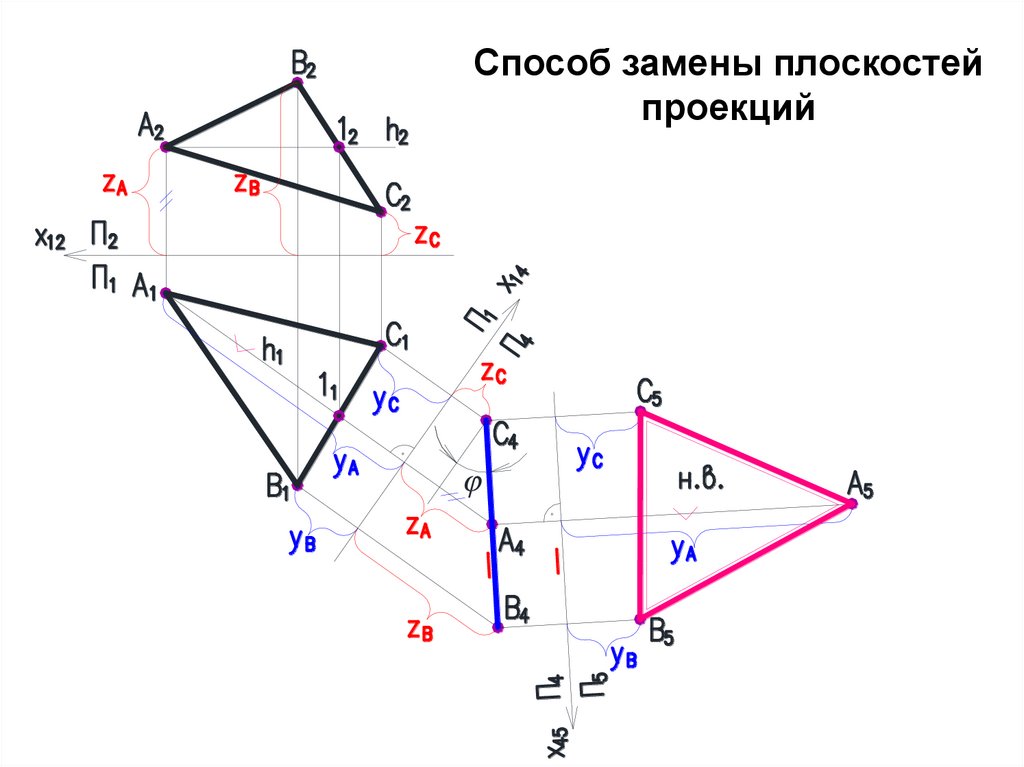
Способ замены плоскостей
проекций