Организация повторения в процессе преподавания математики

1.

Организация повторения в
процессе преподавания
математики

2. Актуальные вопросы для современной школы

как развить у ребенка потребность и
способность искать новое?
как научить его видеть проблемы?
как научить конструировать гипотезы?
как научить детей задавать вопросы?
как научить наблюдать, экспериментировать?
как научить делать умозаключения и выводы?
как научить классифицировать?
как научить давать определения понятиям?

3. Пути решения проблемы повышения и укрепления знаний

Основные принципы методик В.Ф. Шаталова народного учителя СССР и В. Ф. Антонова –
заслуженного учителя АРК.
-опережающее обучение;
-многовариативное повторение;
-изучение материала крупными блоками;
-применение опоры и опорного конспекта;
-решение снизу вверх;
личностно-ориентированный подход;
-открытие перспективы роста и успеха.

4. Повторение материала – одно из важнейших условий его запоминания

Необходимость повторения
обусловлена задачами обучения,
требующими прочного и сознательного
овладения знаниями.
Значение повторения: у учащихся
вырабатывается гибкость, подвижность
ума, обобщённость знаний.

5. Требования, предъявляемые к повторению

1) Когда повторять?
«Учить новое, повторяя, и повторять, изучая новое»
2) Что повторять?
-наиболее важные вопросы, вокруг которых группируется
новый материал
-самое главное и трудное
-такие темы и вопросы, которые недостаточно прочно
усваиваются, которые необходимо обобщить, углубить,
систематизировать.
3) Как повторять?
Применяя дидактические приёмы : анализ, синтез,
сравнение, классификация, обобщение.

6. Виды повторения

Восстанавливающее повторение( в
начале учебного года или в начале
темы)
текущее повторение
тематическое повторение
заключительное повторение(в конце
учебного года или курса школы 9 или 11
класс).

7. Приёмы организации повторения

первичной
проверки
игра
Деловая
«Найди себя в теме»
обобщения
контроля
подведения
Рефлексия
урока
Этап
домашнем задании
о
и
итогов
информирования
Этап коррекции
самоконтроля
в Этап
систематизации
Этап
домашнее Этап
Показательный отчёт
задание
Обговариваем
Заполни пропуски
компетентность
тем
Перекрёсток
рынок возможностей,
и
Этап закрепления изученного
понимания изученного
Этап
Дебаты «за» и «против», Этап применения изученного
«Экспресс-тест»
Повторяем с контролем
и способов деятельности
Этап изучения новых знаний
знаний
домашнего
актуализации
учащихся
своего Этап
Повторяем с расширением
конспекта
проверки
задания
парах, Этап
«Поймай Организационный этап
примеры»
в
опора»,
Составление
«Свои
Работа
ошибку»
«Своя
Приёмы организации повторения

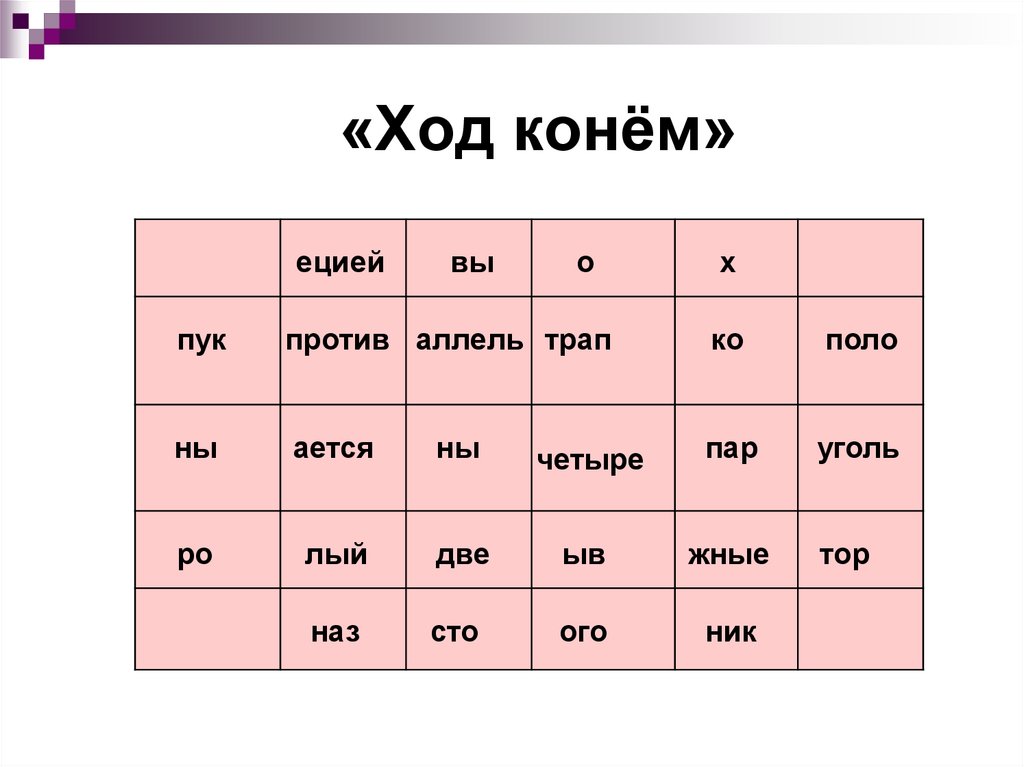
8. «Ход конём»

ецией
вы
о
х
пук
против аллель трап
ко
поло
ны
ается
ны
четыре
пар
уголь
ро
лый
две
ыв
жные
наз
сто
ого
ник
тор

9. Устный счёт «ДОМИНО»

x
2x
5x
10 x
2
sin x
1
x
2
x 1
1
(4 x 3 )
3
(ln x)
cos x
44 x
18x
2x
2
log x
1
x ln x
( x )
1
3 x
3
3
3
sin x
2
tgx
cos x
1
cos x
2
x 4
2
6x
3

10. Задачи на отработку понятий для текущего повторения

Какая связь между равнобедренным
треугольником и ромбом? Какие свойства
ромба являются следствием свойств
равнобедренного треугольника?
Что это за четырёхугольник , у которого
диагональ перпендикулярна двум неравным
сторонам? А если эта диагональ
перпендикулярна двум равным сторонам?
Укажите не менее 8 свойств числа 16
Что вы можете сказать
о выражении
?

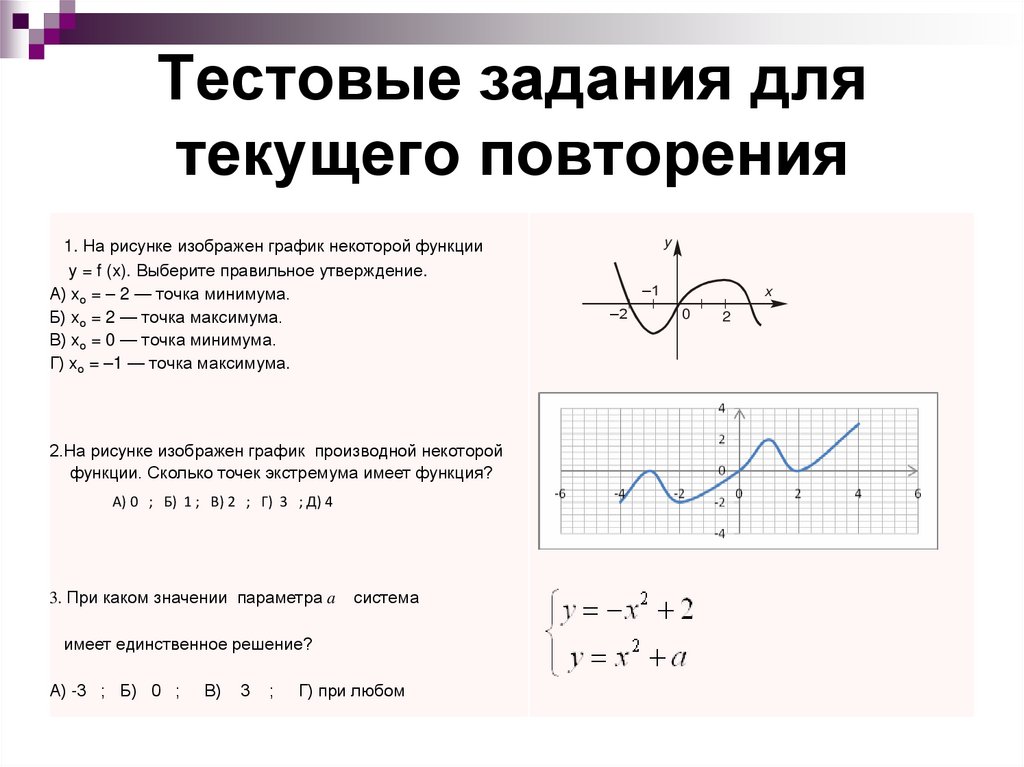
11. Тестовые задания для текущего повторения

1. На рисунке изображен график некоторой функции
y = f (x). Выберите правильное утверждение.
А) хо = – 2 — точка минимума.
Б) хо = 2 — точка максимума.
В) хо = 0 — точка минимума.
Г) хо = –1 — точка максимума.
2.На рисунке изображен график производной некоторой
функции. Сколько точек экстремума имеет функция?
А) 0 ; Б) 1 ; В) 2 ; Г) 3 ; Д) 4
3. При каком значении параметра a
система
имеет единственное решение?
А) -3 ; Б) 0 ;
В)
3
;
Г) при любом
y
–1
–2
x
0
2

12. Набор упражнений для итогового повторения

Модуль числа.
Элементарные функции (их графики,
свойства, область определения)
Производная, её механический и
геометрический смысл
Монотонность и экстремумы функции
Исследование функции с помощью
производной и построение графика функции

13. Интеллектуальные конкурсы

« Что? Где? Когда?»
«Вокруг да около тригонометрии»
«Математик-бизнесмен»
«Математический бой»
«А вы знаете, что…»
ПОДГОТОВКА КОМАНД УЧАЩИХСЯ К
ГОРОДСКИМ ИГРАМ «ЛИНГВИСТ», «ФИЗИКО-МАТЕМАТИЧЕСКИЙ
БОЙ», конкурсу «ЛИМОН»