Основні поняття стереометрії. Аксіоми стереометрії. Наслідки з аксіом стереометрії

1.

Основні поняття
стереометрії.
Аксіоми
стереометрії.
Наслідки з
аксіом
стереометрії

2.

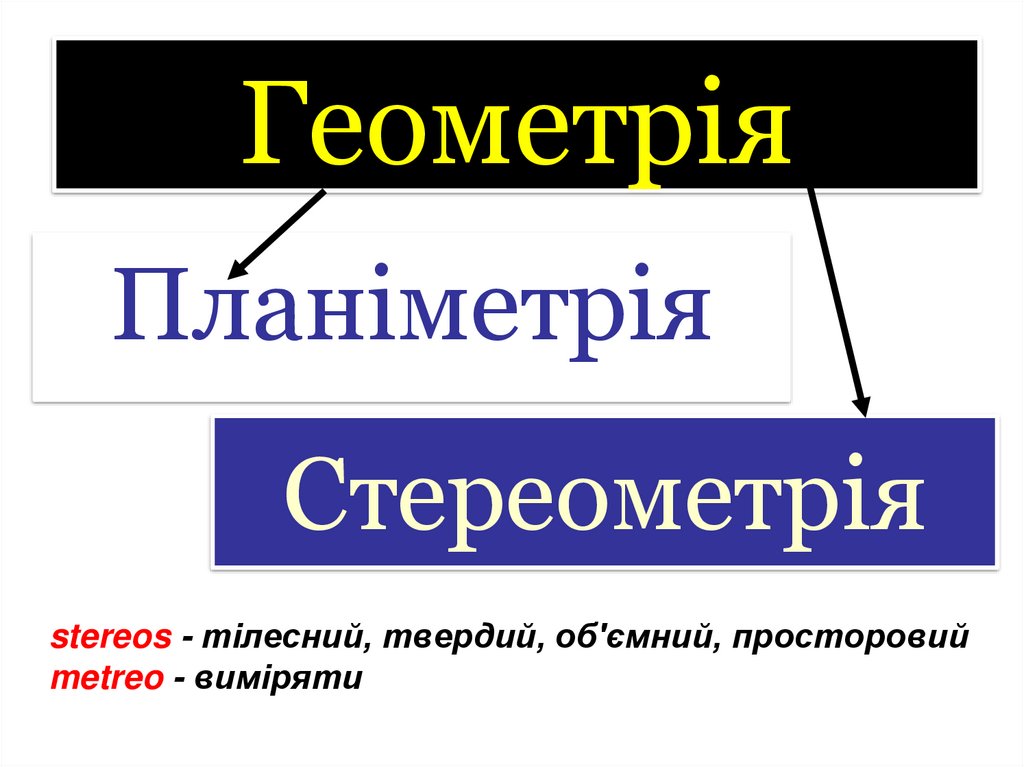
Геометрія
Планіметрія
Стереометрія
stereos - тілесний, твердий, об'ємний, просторовий
metreo - виміряти

3.

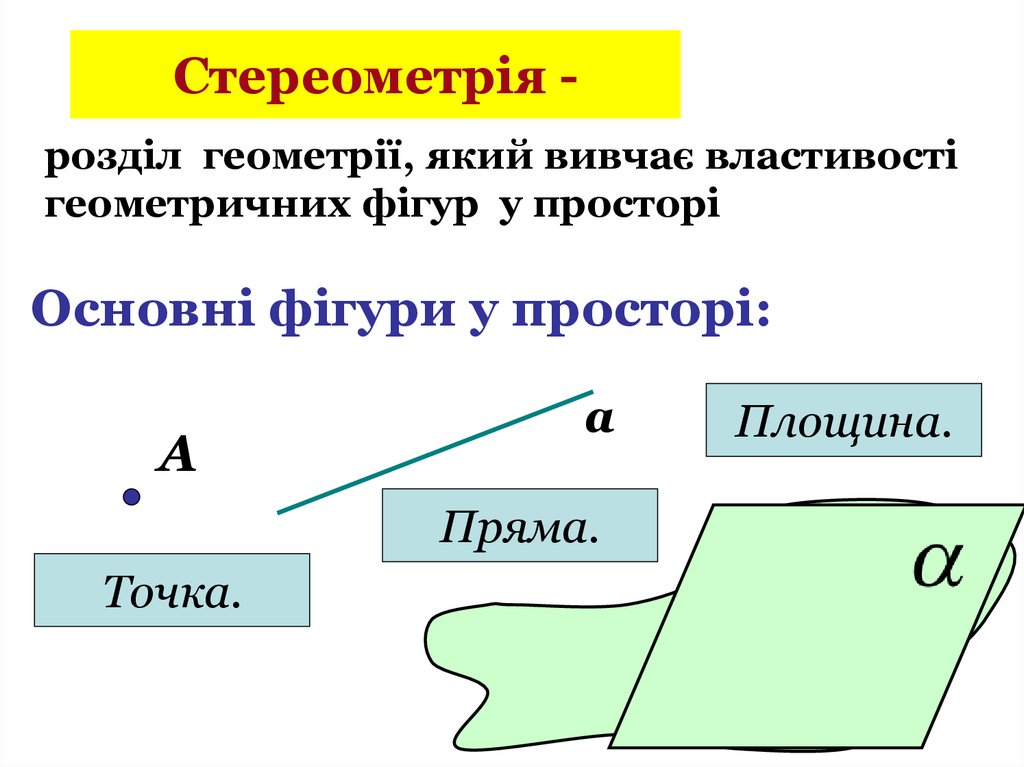
Стереометрія розділ геометрії, який вивчає властивості
геометричних фігур у просторі
Основні фігури у просторі:
А
а
Пряма.
Точка.
Площина.

4.

Основні геометричні
фігури позначають:
Точка
A, B, C, …
Пряма
Площина
a, b, c, …
або
AВ, BС, CD, …

5.

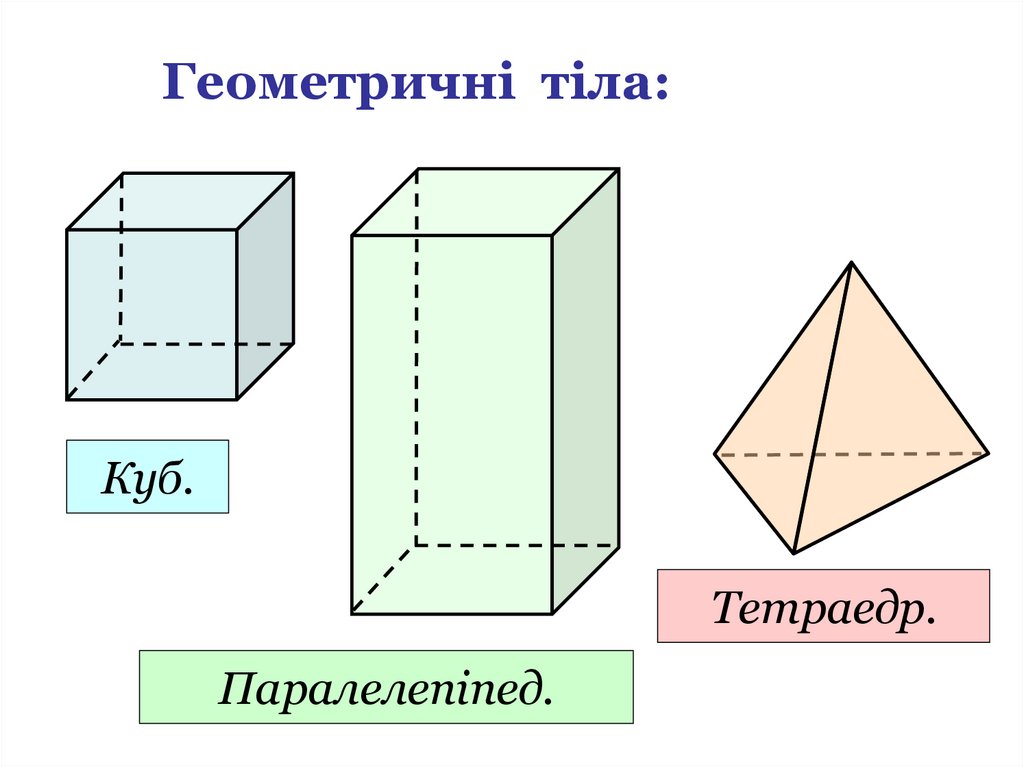
Геометричні тіла:
Куб.
Тетраедр.
Паралелепіпед.

6.

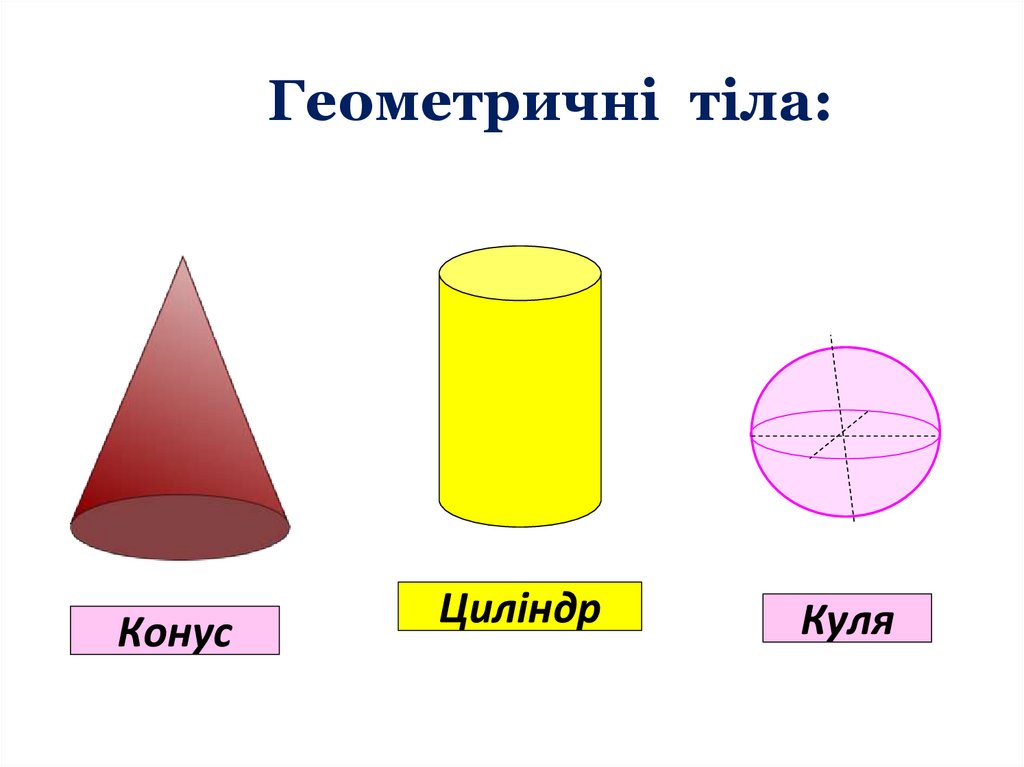
Геометричні тіла:
Конус
Циліндр
Куля

7.

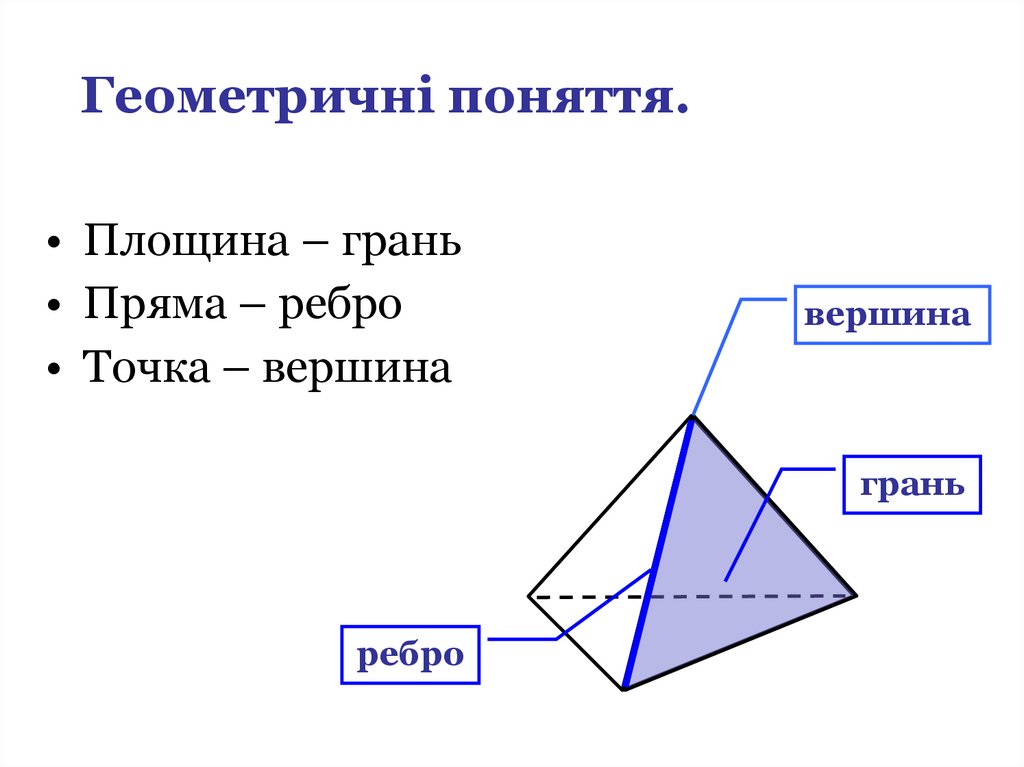
Геометричні поняття.
• Площина – грань
• Пряма – ребро
• Точка – вершина
вершина
грань
ребро

8.

Аксіома
(греч. axíõma – приняття положення)
твердження наукової теорії, яке не
потребує доведення
Памятайте!!
властивості всіх фігур,
які ви вивчали в планіметрії,
справджуються в кожній площині
простору;

9.

10.

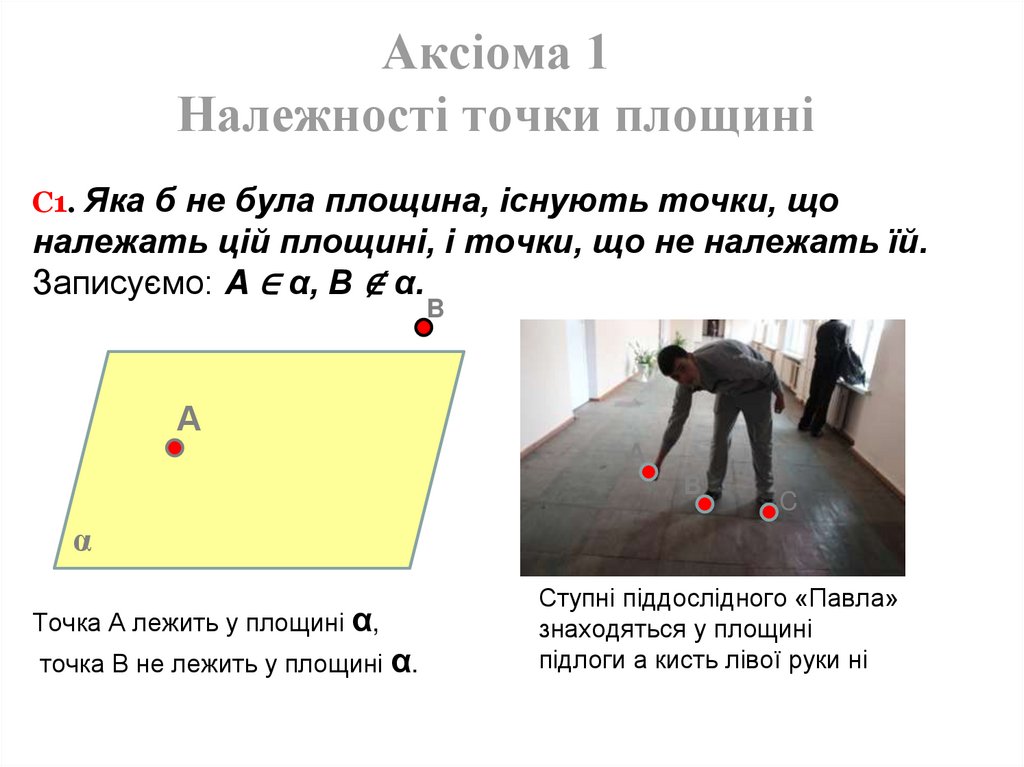
Аксіома 1
Належності точки площині
С1. Яка б не була площина, існують точки, що
належать цій площині, і точки, що не належать їй.
Записуємо: A ∈ α, B ∉ α.
B
А
A
B
C
α
Точка А лежить у площині α,
точка B не лежить у площині α.
Ступні піддослідного «Павла»
знаходяться у площині
підлоги а кисть лівої руки ні

11.

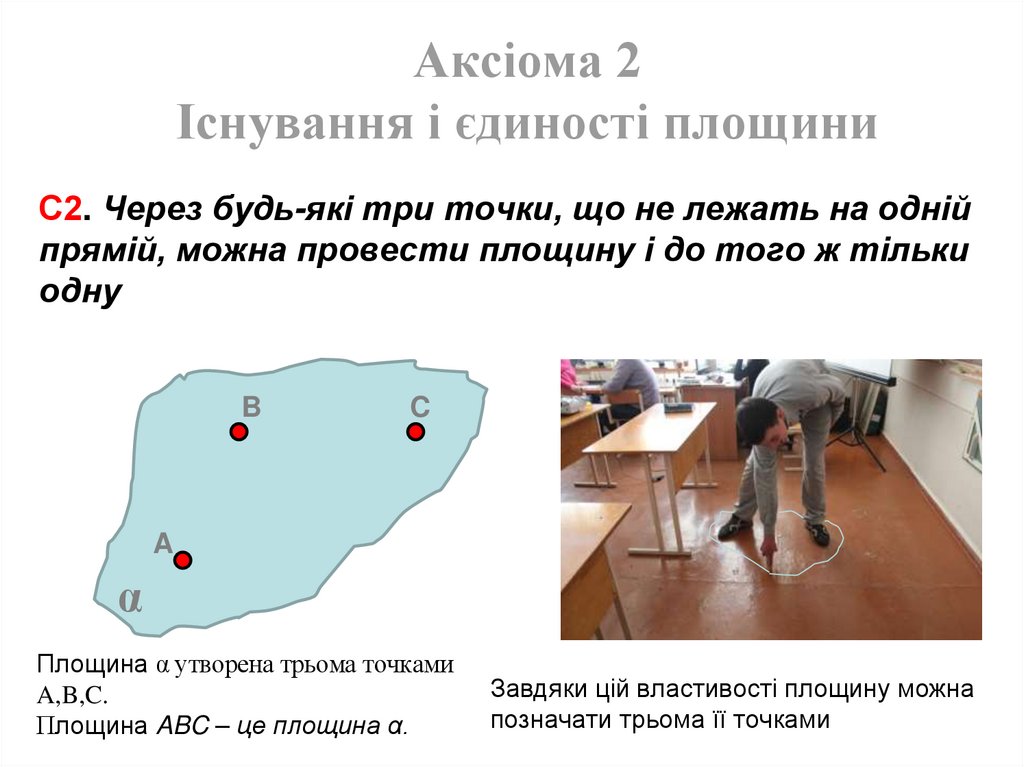
Аксіома 2
Існування і єдиності площини
С2. Через будь-які три точки, що не лежать на одній
прямій, можна провести площину і до того ж тільки
одну
B
C
A
α
Площина α утворена трьома точками
A,B,C.
Площина ABC – це площина α.
Завдяки цій властивості площину можна
позначати трьома її точками

12.

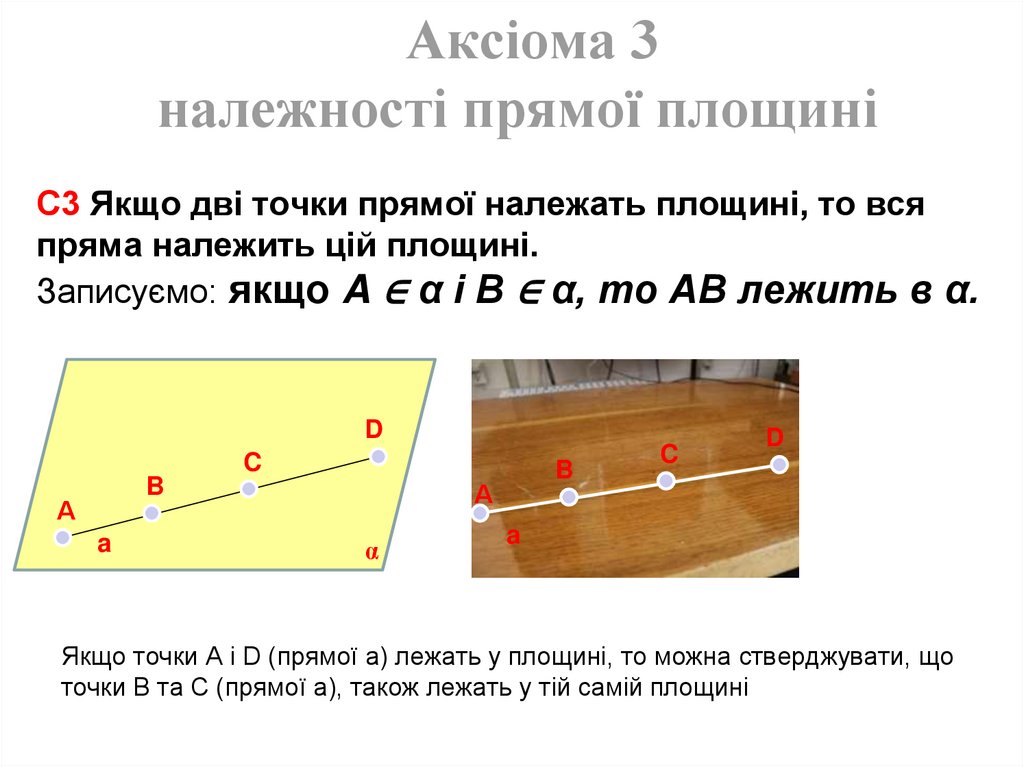
Аксіома 3
належності прямої площині
С3 Якщо дві точки прямої належать площині, то вся
пряма належить цій площині.
Записуємо: якщо A ∈ α і B ∈ α, то AB лежить в α.
D
C
B
А
a
B
А
α
C
D
a
Якщо точки А і D (прямої a) лежать у площині, то можна стверджувати, що
точки B та С (прямої a), також лежать у тій самій площині

13.

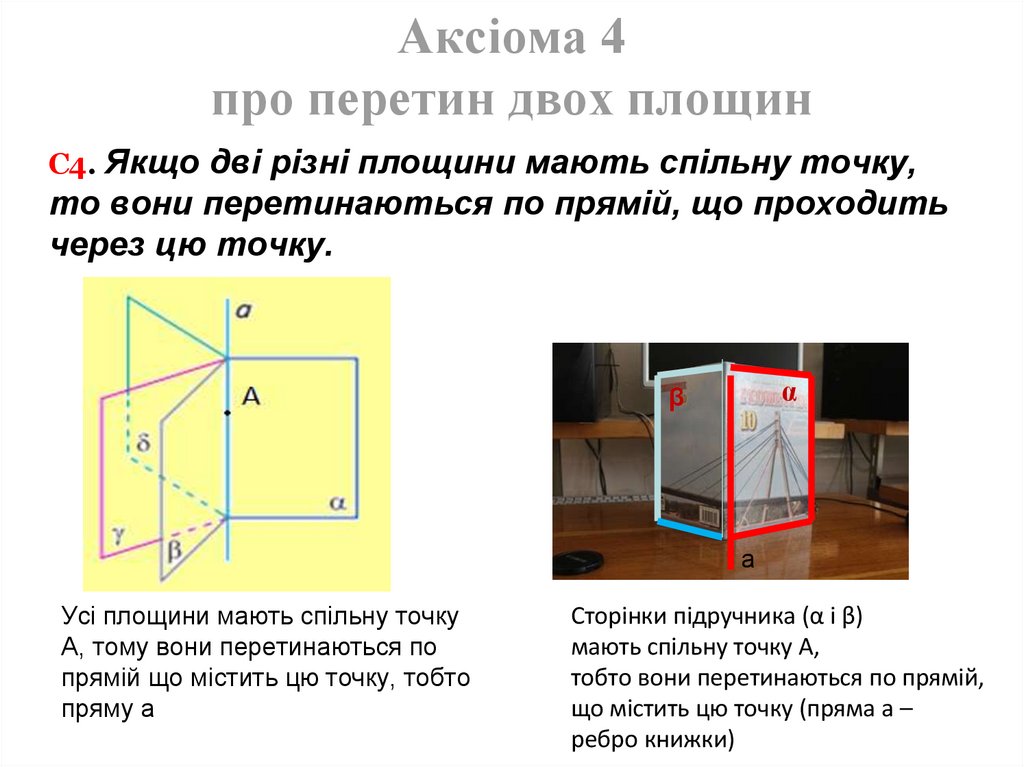
Аксіома 4
про перетин двох площин
С4. Якщо дві різні площини мають спільну точку,
то вони перетинаються по прямій, що проходить
через цю точку.
α
β
а
Усі площини мають спільну точку
А, тому вони перетинаються по
прямій що містить цю точку, тобто
пряму а
Сторінки підручника (α і β)
мають спільну точку А,
тобто вони перетинаються по прямій,
що містить цю точку (пряма а –
ребро книжки)

14.

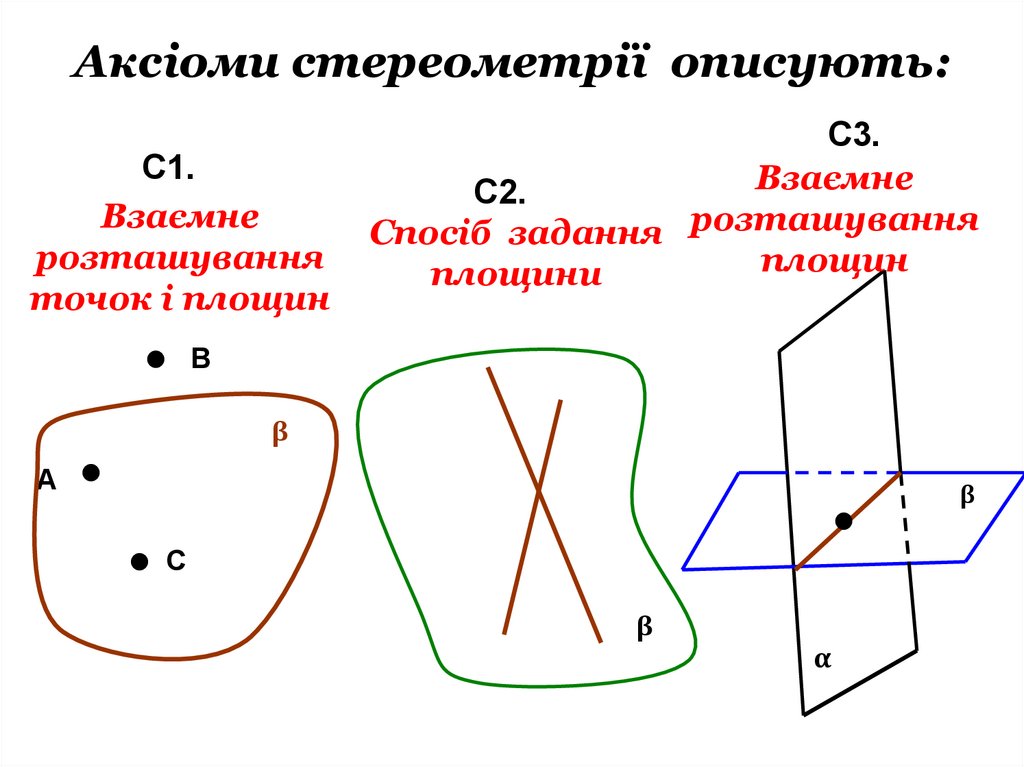
Аксіоми стереометрії описують:
С1.
Взаємне
розташування
точок і площин
С3.
Взаємне
С2.
Спосіб задання розташування
площин
площини
В
β
А
β
С
β
α

15.

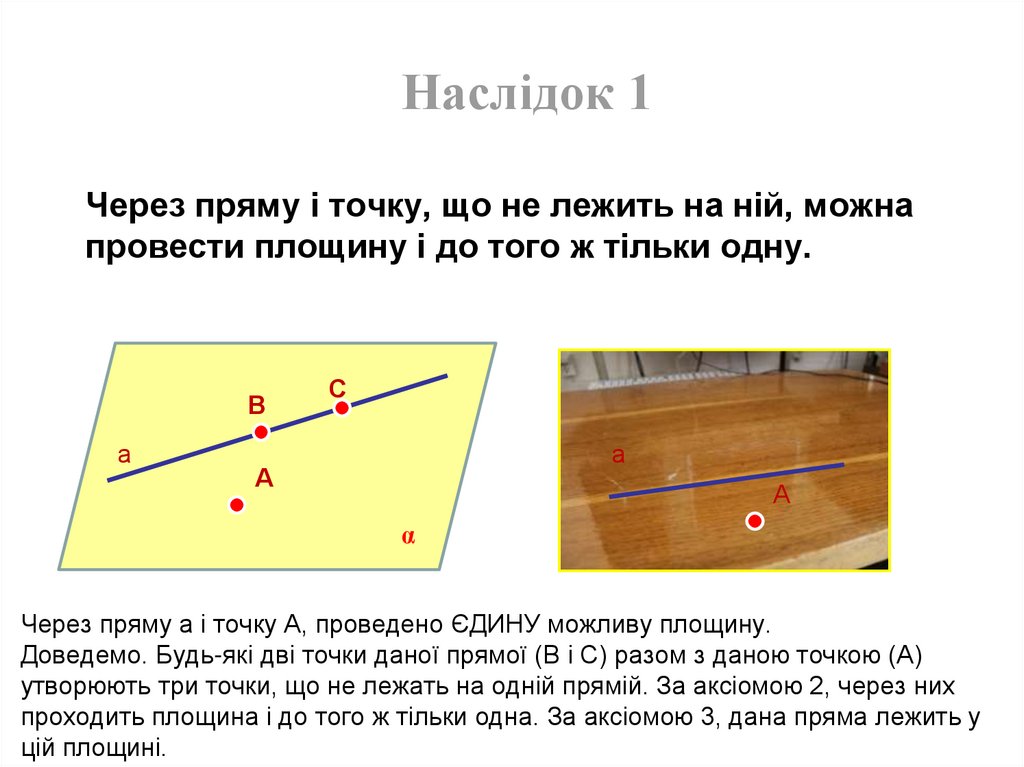
Наслідок 1
Через пряму і точку, що не лежить на ній, можна
провести площину і до того ж тільки одну.
В
а
С
а
А
А
α
Через пряму a і точку А, проведено ЄДИНУ можливу площину.
Доведемо. Будь-які дві точки даної прямої (В і С) разом з даною точкою (А)
утворюють три точки, що не лежать на одній прямій. За аксіомою 2, через них
проходить площина і до того ж тільки одна. За аксіомою 3, дана пряма лежить у
цій площині.

16.

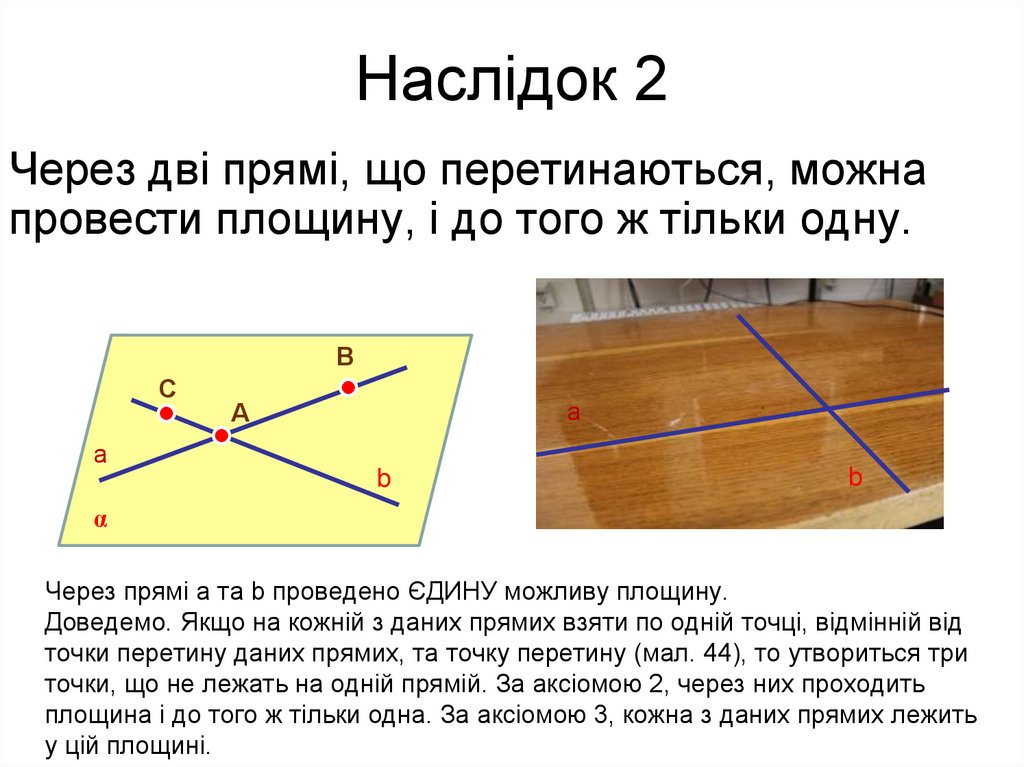
Наслідок 2
Через дві прямі, що перетинаються, можна
провести площину, і до того ж тільки одну.
В
С
а
А
а
b
b
α
Через прямі а та b проведено ЄДИНУ можливу площину.
Доведемо. Якщо на кожній з даних прямих взяти по одній точці, відмінній від
точки перетину даних прямих, та точку перетину (мал. 44), то утвориться три
точки, що не лежать на одній прямій. За аксіомою 2, через них проходить
площина і до того ж тільки одна. За аксіомою 3, кожна з даних прямих лежить
у цій площині.

17.

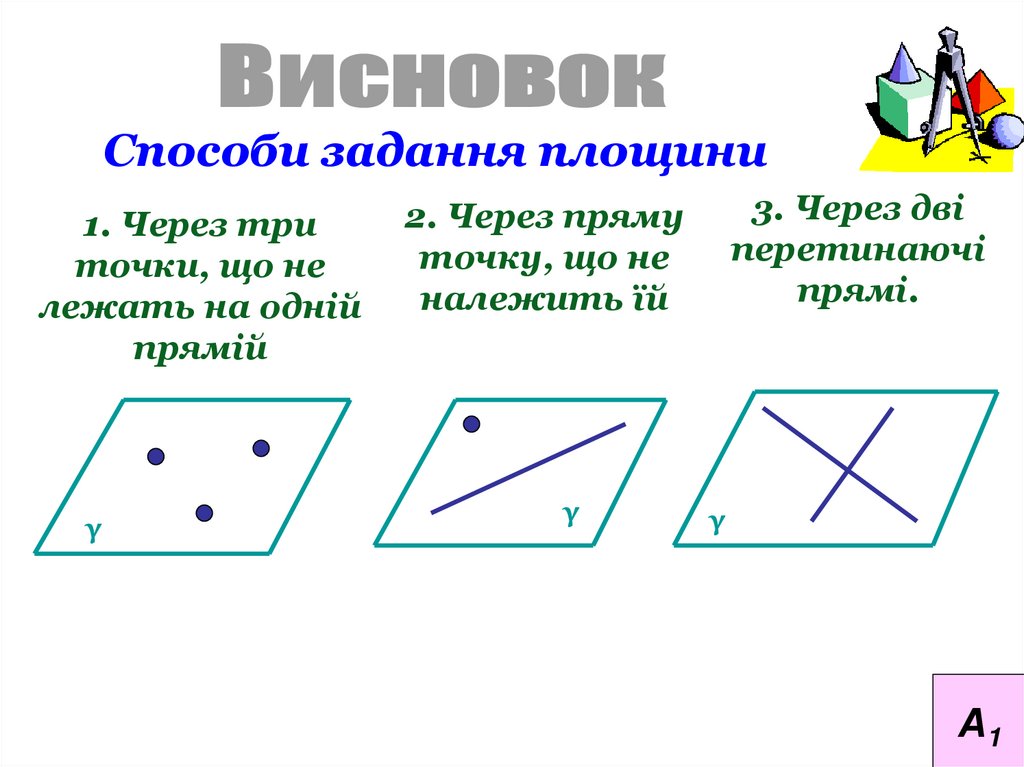
Способи задання площини
1. Через три
точки, що не
лежать на одній
прямій
γ
3. Через дві
перетинаючі
прямі.
2. Через пряму
точку, що не
належить їй
γ
γ
А1

18.

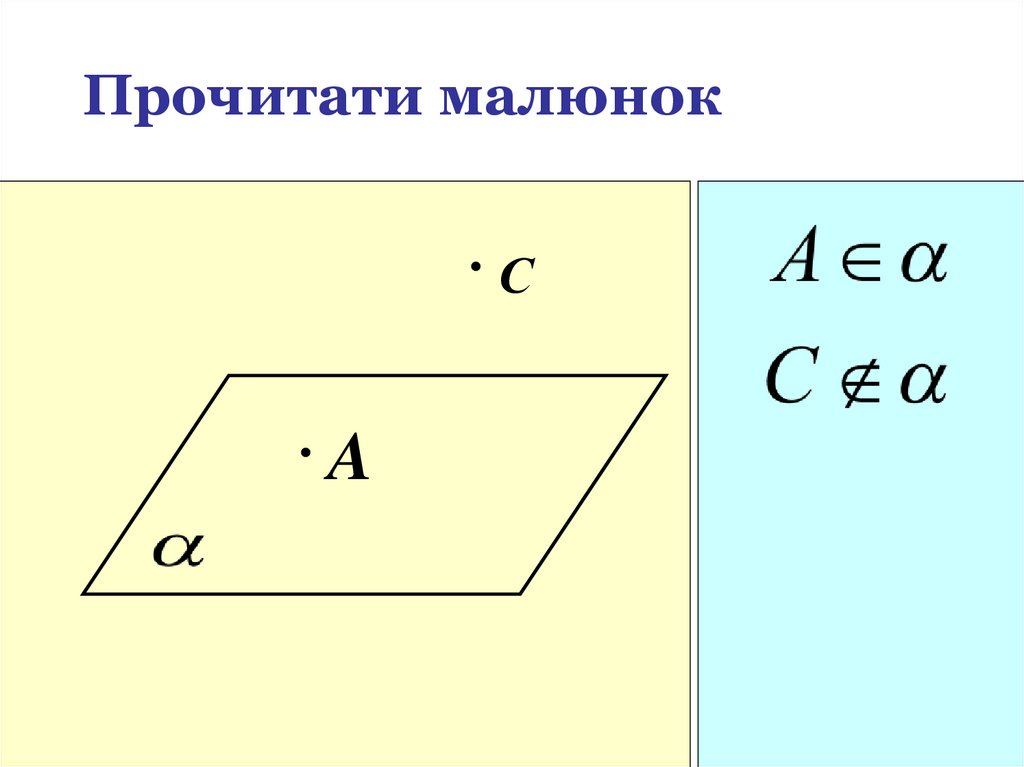
Прочитати малюнок
С
A

19.

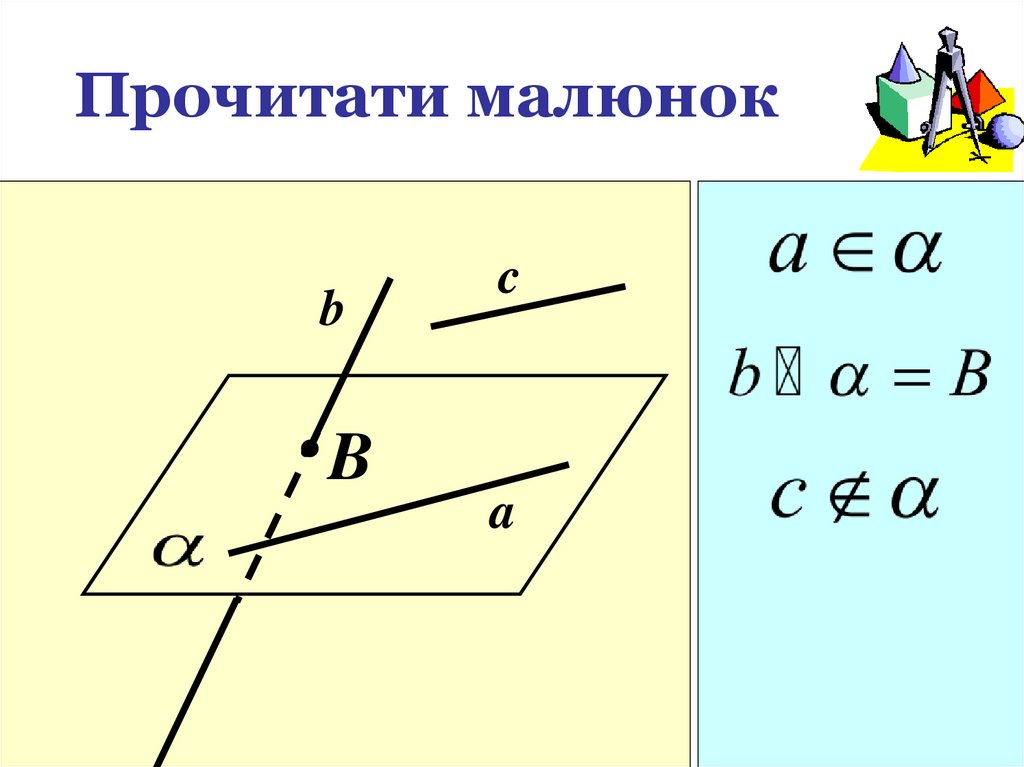
Прочитати малюнок
b
B
c
a

20.

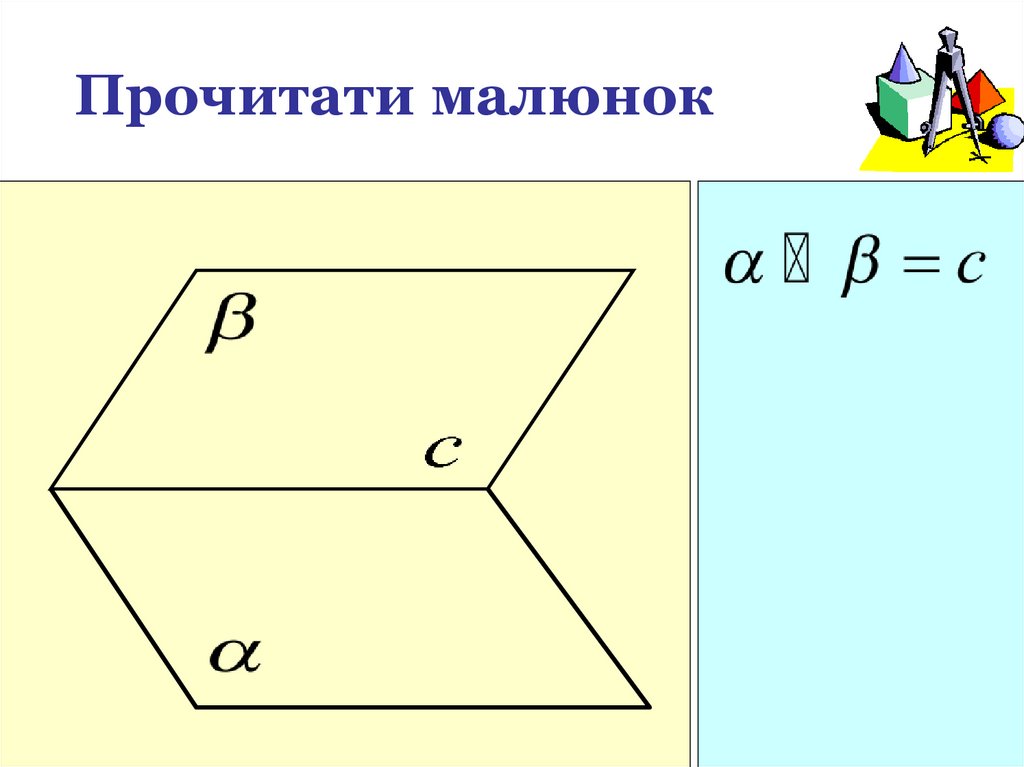
Прочитати малюнок

21.

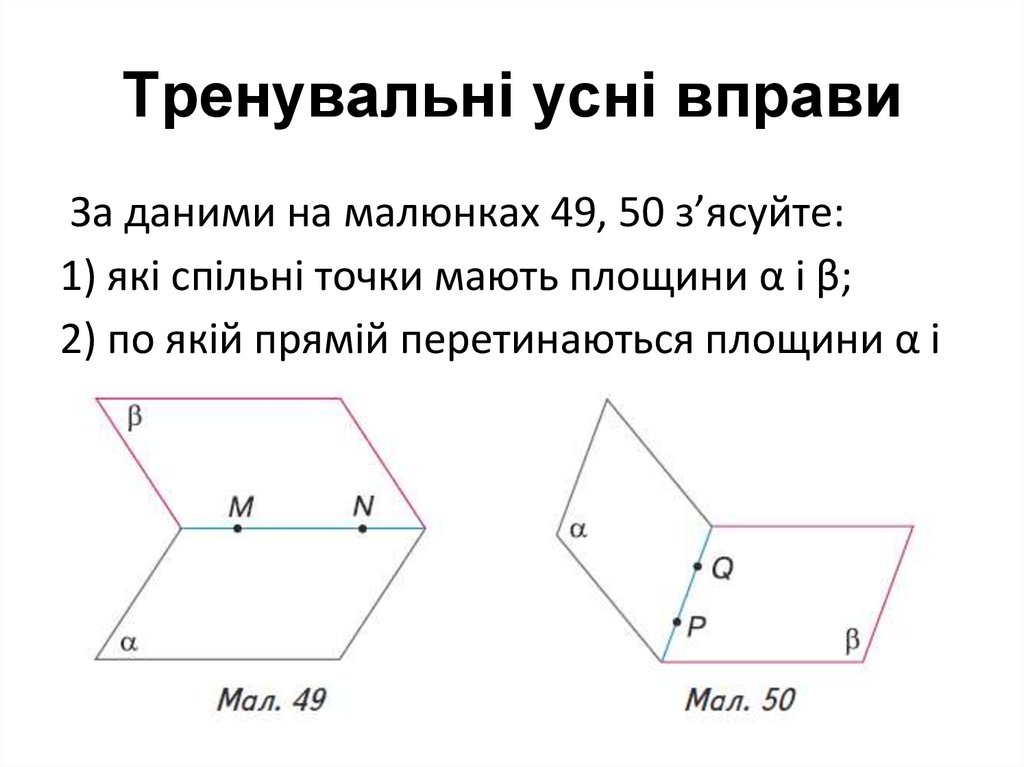
Тренувальні усні вправи
За даними на малюнках 49, 50 з’ясуйте:
1) які спільні точки мають площини α і β;
2) по якій прямій перетинаються площини α і
β.

22.

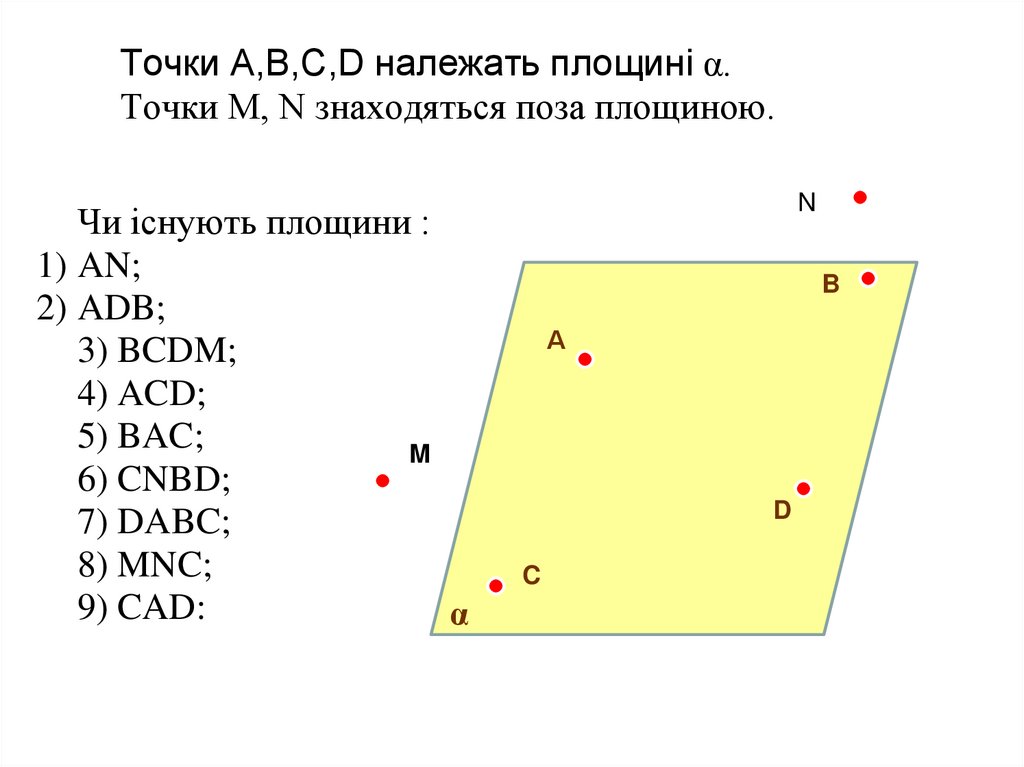
Точки A,B,C,D належать площині α.
Точки M, N знаходяться поза площиною.
Чи існують площини :
1) AN;
2) ADB;
3) BCDM;
4) ACD;
5) BAC;
M
6) CNBD;
7) DABC;
8) MNC;
9) CAD:
α
N
B
А
D
C

23.

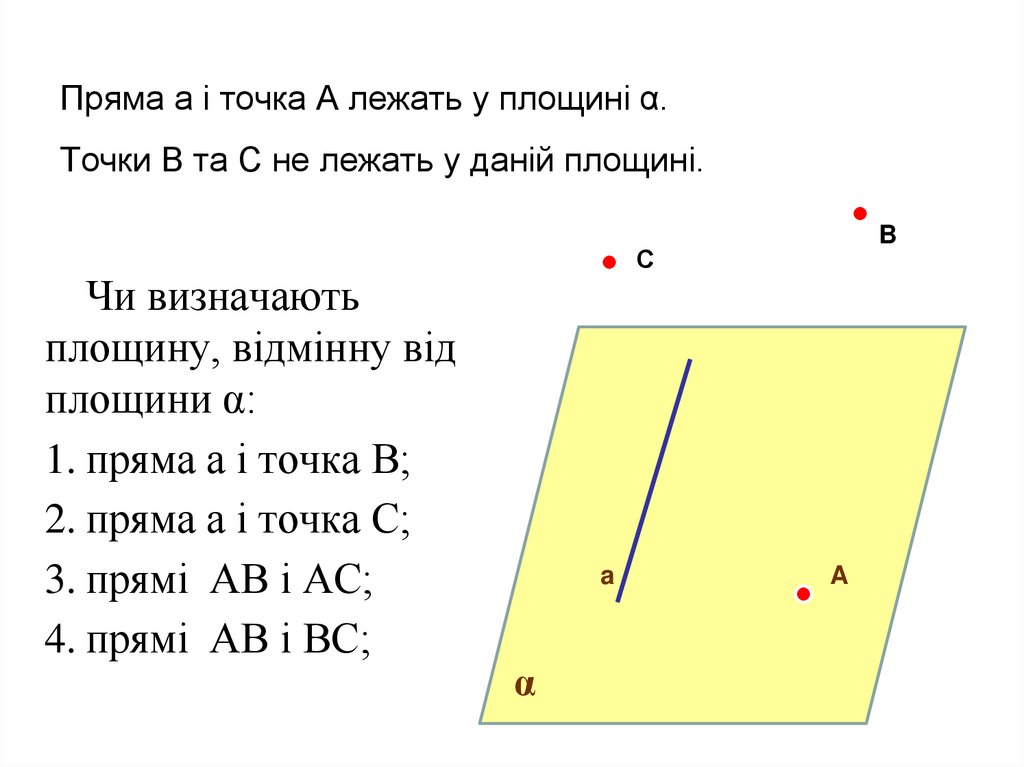
Пряма а і точка А лежать у площині α.
Точки B та C не лежать у даній площині.
Чи визначають
площину, відмінну від
площини α:
1. пряма а і точка B;
2. пряма а і точка C;
3. прямі AB і AC;
4. прямі AB і BC;
B
С
a
α
A

24.

25.

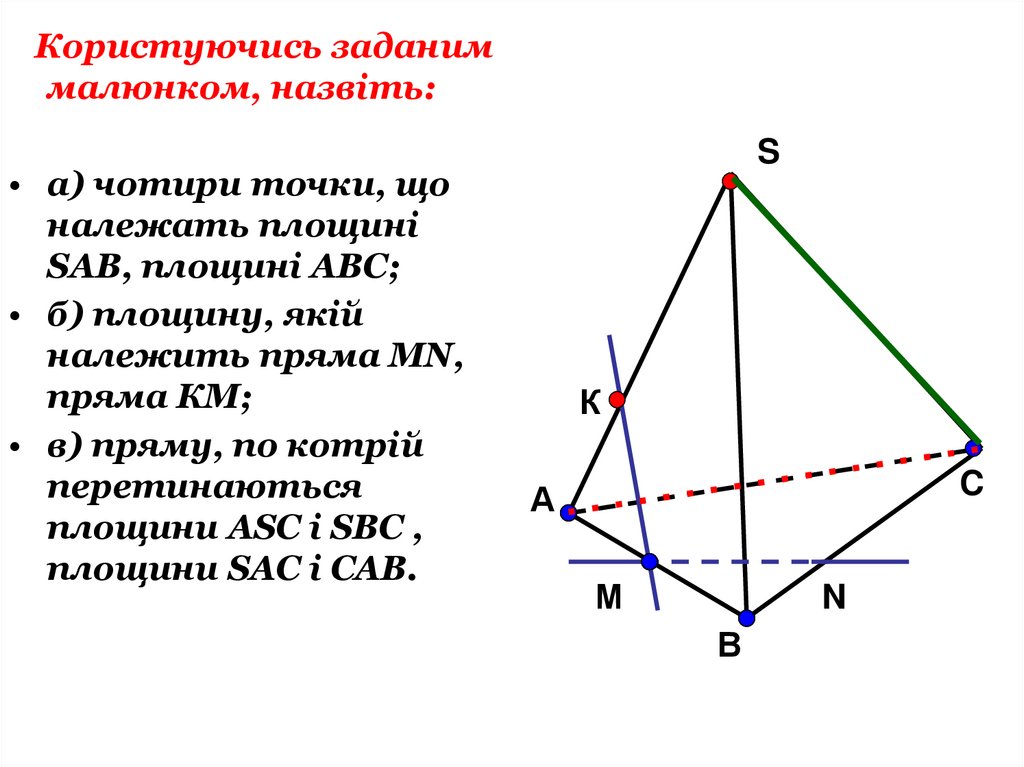
Користуючись заданим
малюнком, назвіть:
• а) чотири точки, що
належать площині
SAB, площині АВС;
• б) площину, якій
належить пряма MN,
пряма КМ;
• в) пряму, по котрій
перетинаються
площини ASC і SBC ,
площини SAC і CAB.
S
К
C
А
М
N
В

26.

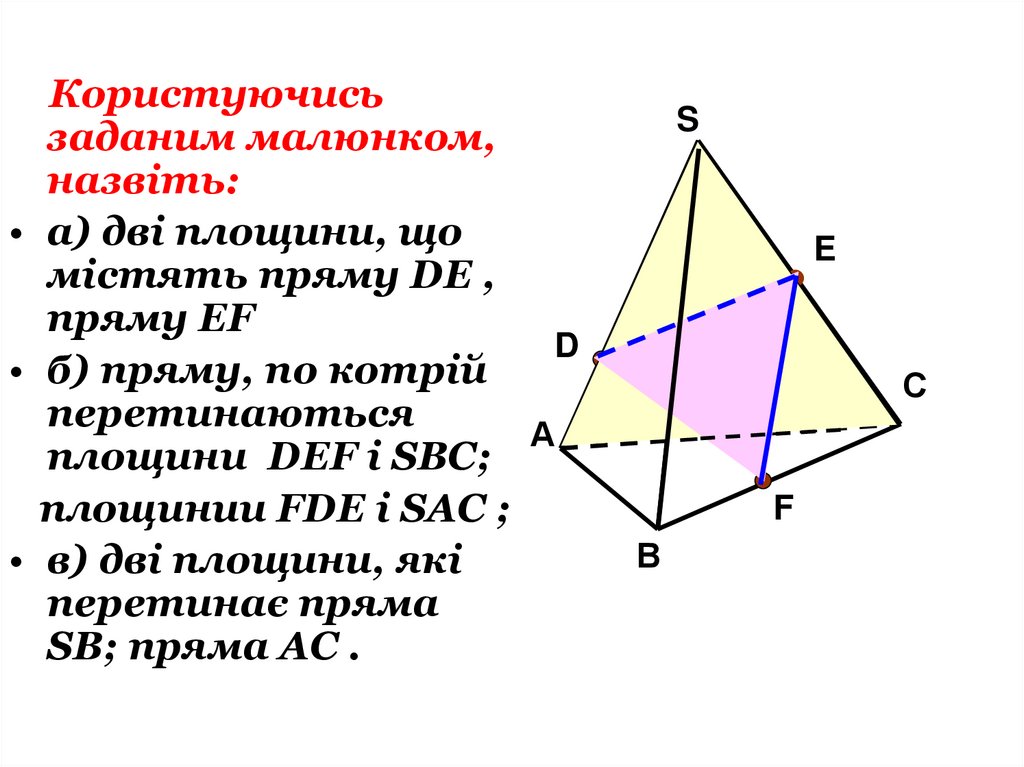
Користуючись
заданим малюнком,
назвіть:
• а) дві площини, що
містять пряму DE ,
пряму EF
D
• б) пряму, по котрій
перетинаються
А
площини DEF і SBC;
площинии FDE і SAC ;
• в) дві площини, які
перетинає пряма
SB; пряма AC .
S
E
С
F
В

27.

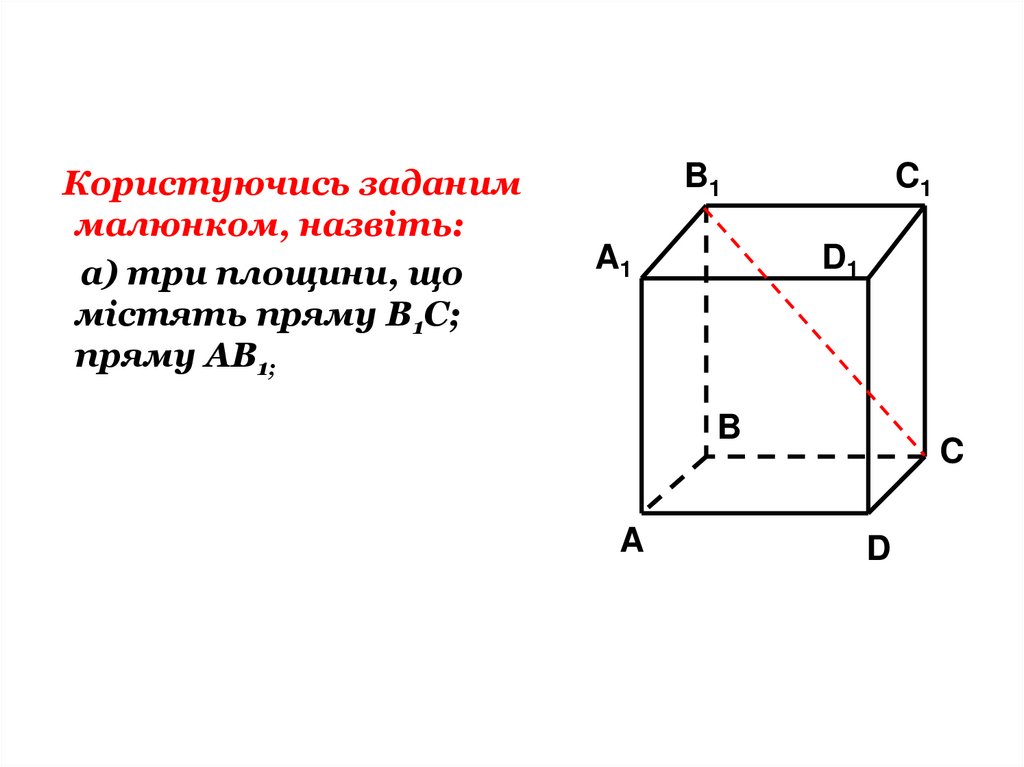
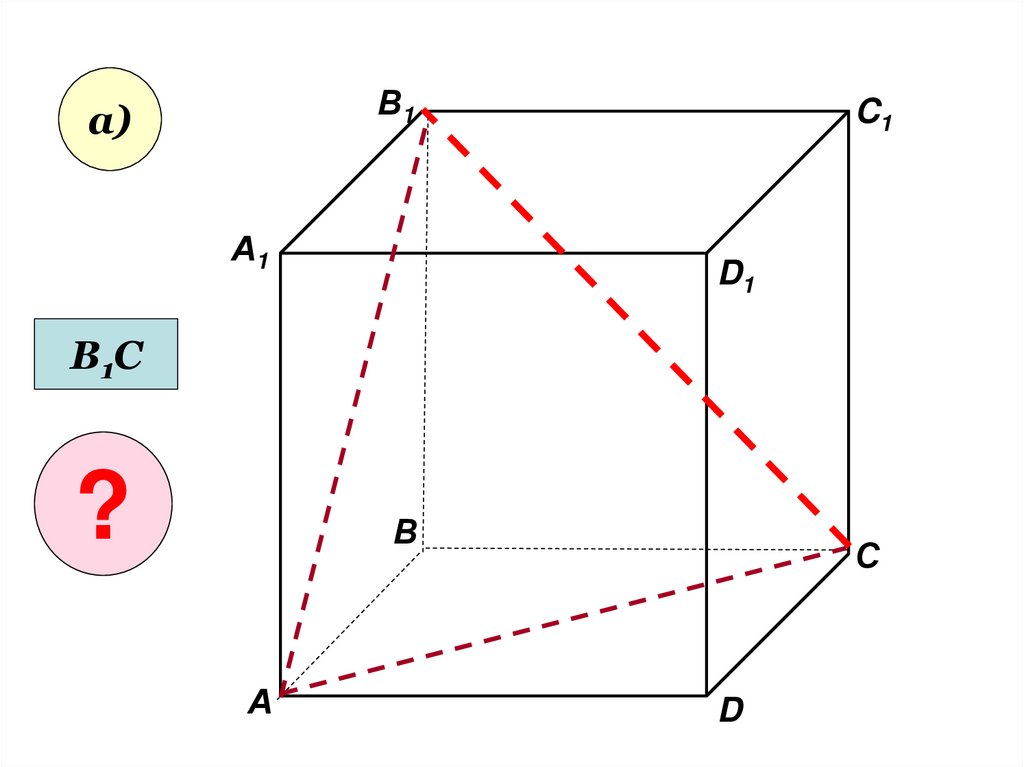
Користуючись заданим
малюнком, назвіть:
а) три площини, що
містять пряму В1С;
пряму АВ1;
B1
A1
C1
D1
B
A
C
D

28.

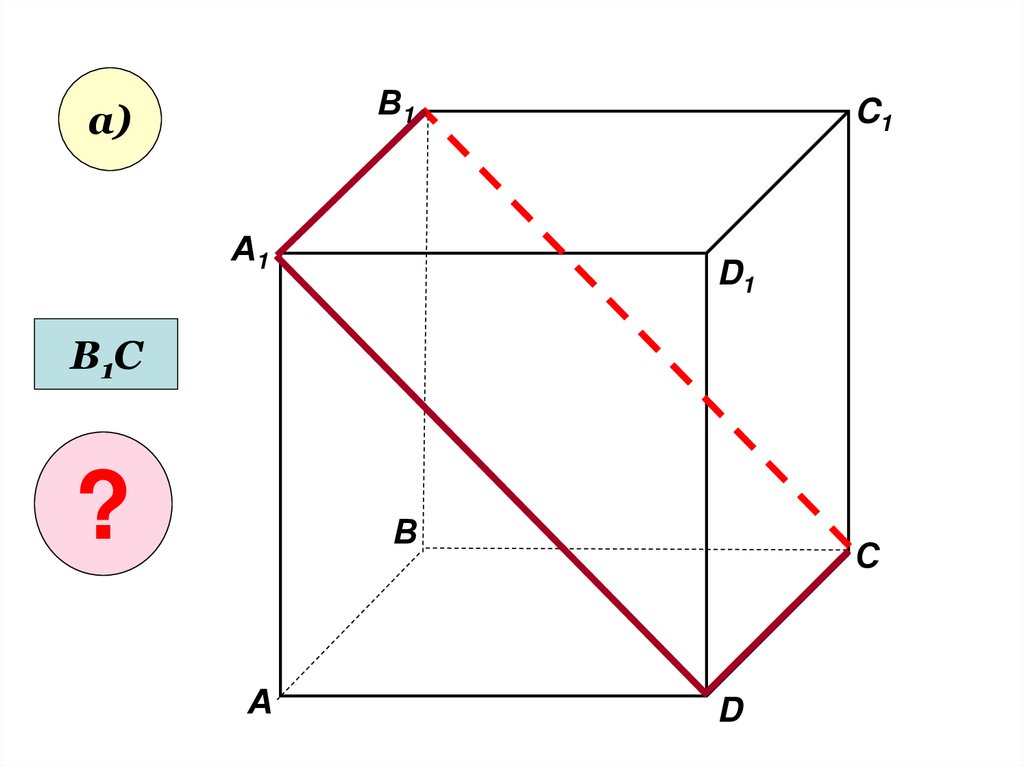
В1
а)
А1
C1
D1
В1С
?
В
А
С
D

29.

В1
а)
А1
C1
D1
В1С
?
В
А
С
D

30.

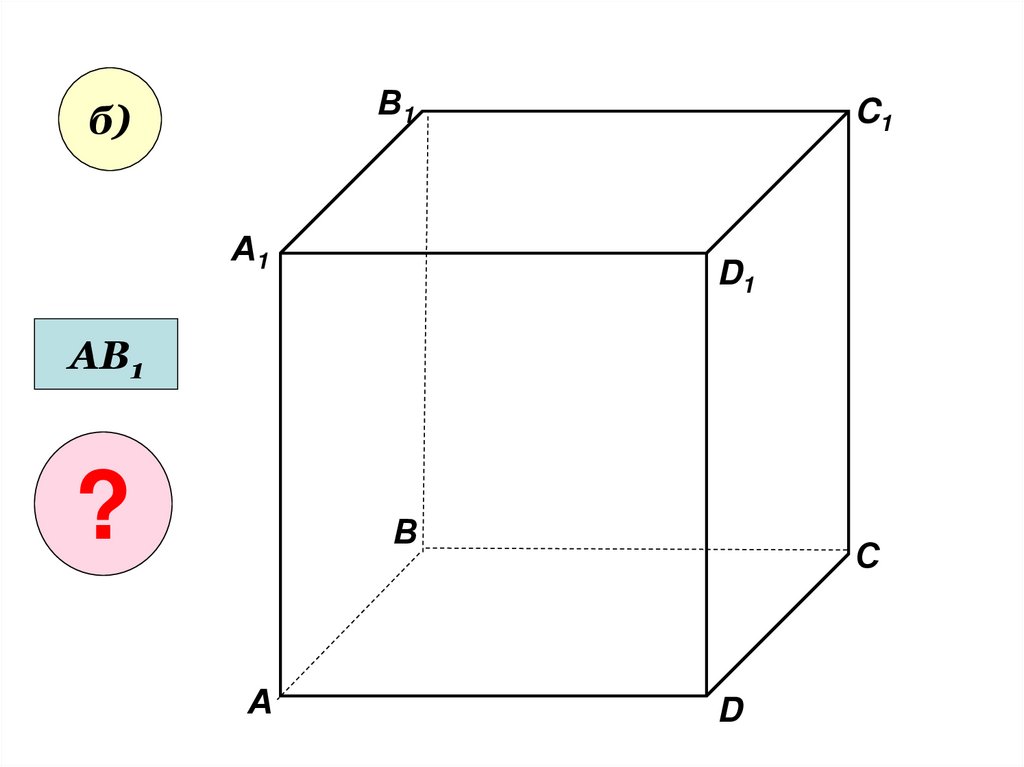
В1
б)
А1
C1
D1
АВ1
?
В
А
С
D

31.

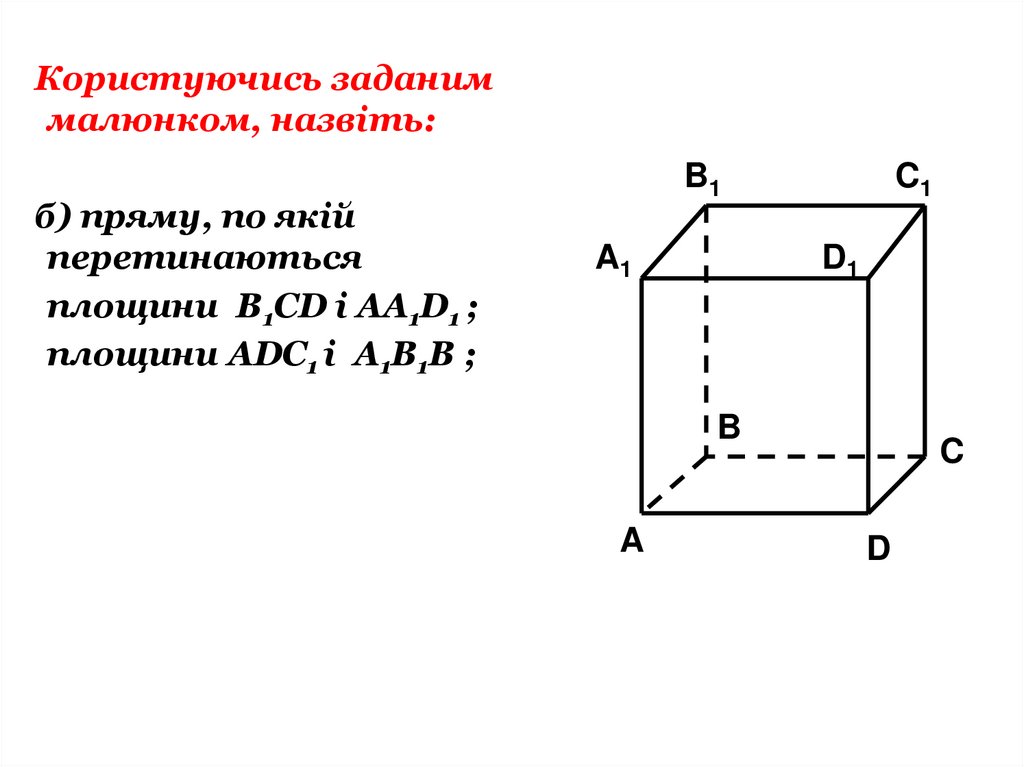
Користуючись заданим
малюнком, назвіть:
б) пряму, по якій
перетинаються
площини B1CD і AA1D1 ;
площини ADC1 і A1B1B ;
B1
A1
C1
D1
B
A
C
D

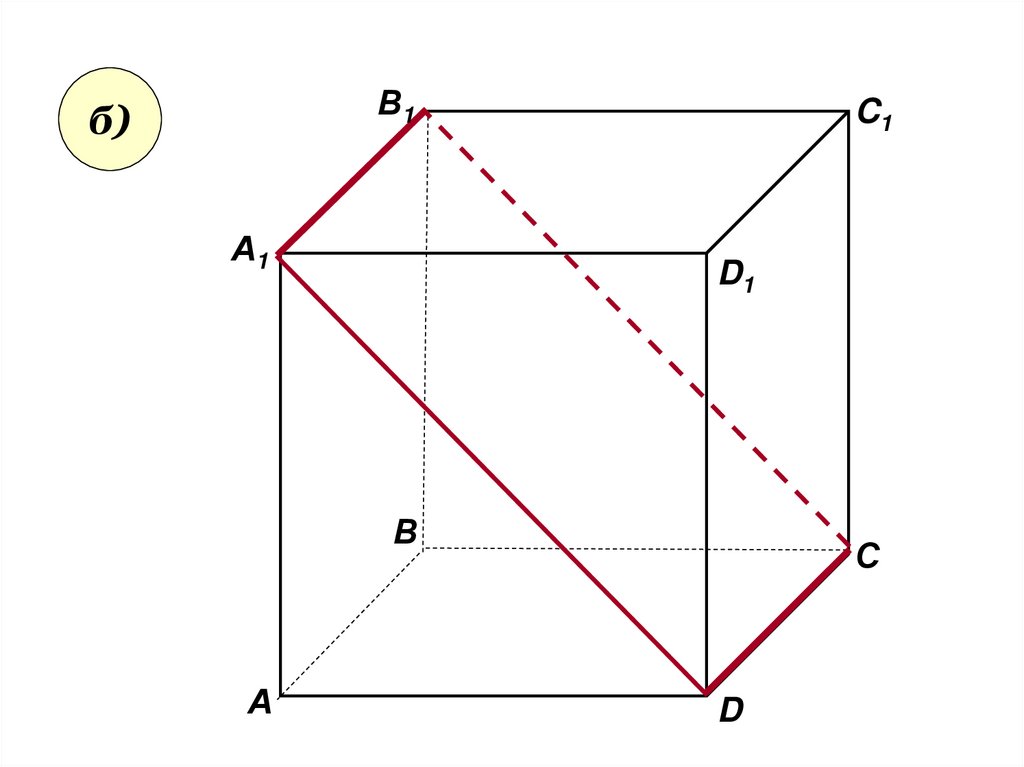
32.

В1
б)
А1
C1
D1
В
А
С
D

33.

В1
в)
А1
C1
D1
В
А
С
D

34.

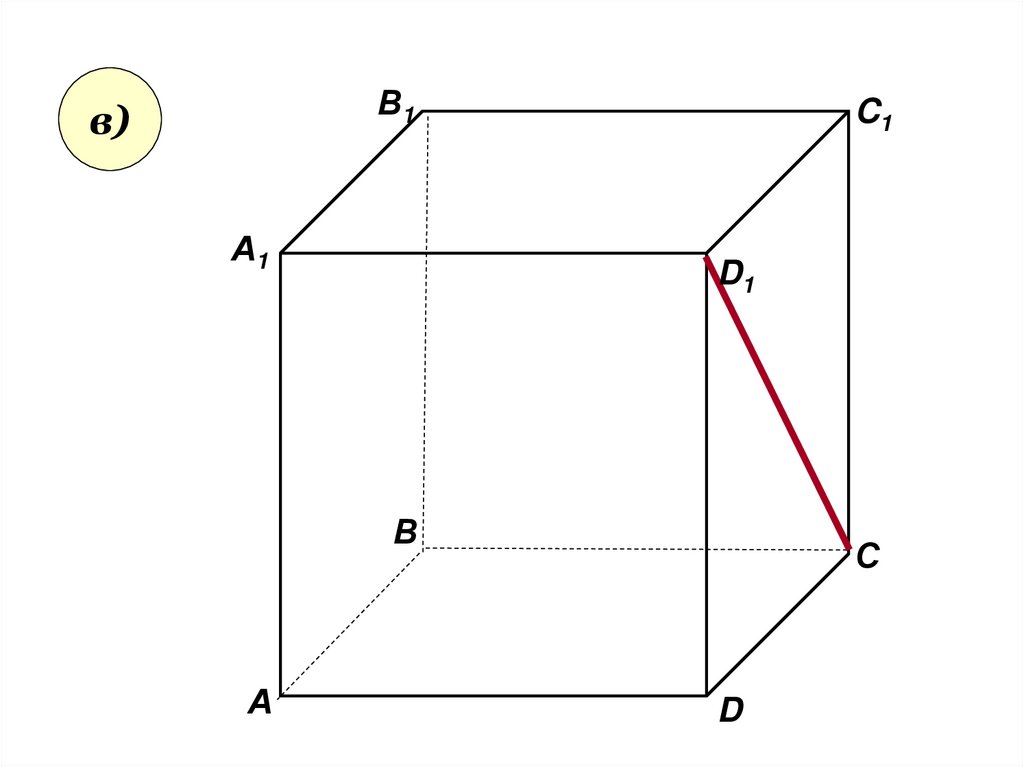
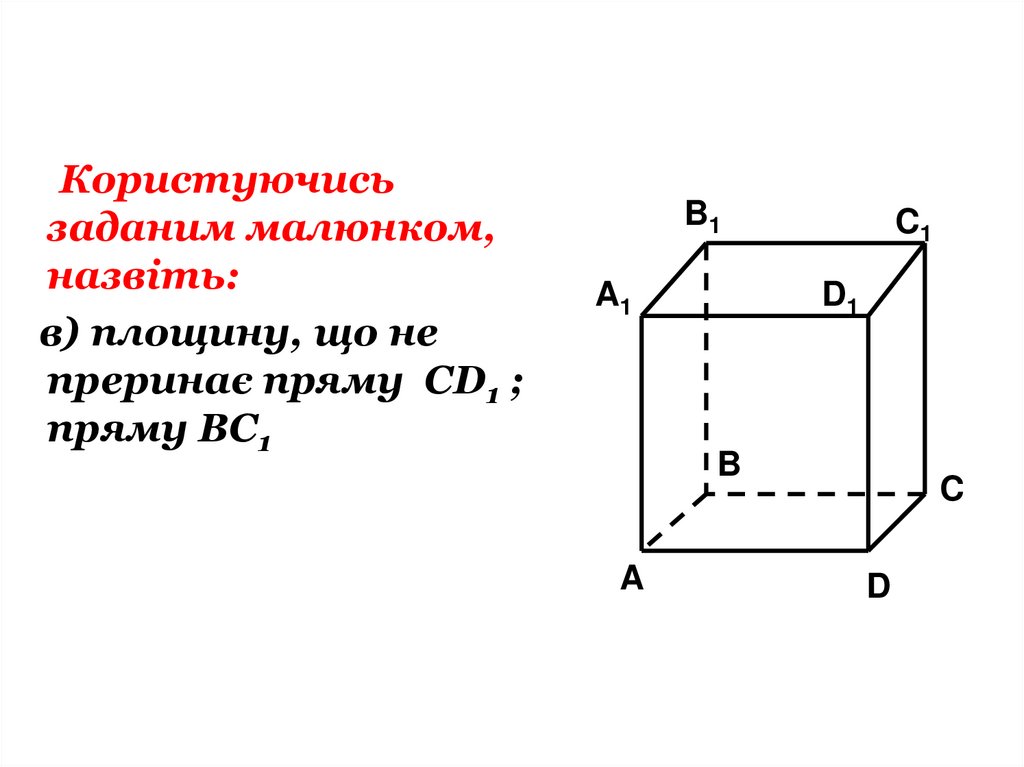
Користуючись
заданим малюнком,
назвіть:
в) площину, що не
преринає пряму CD1 ;
пряму BC1
B1
A1
C1
D1
B
A
C
D

35.

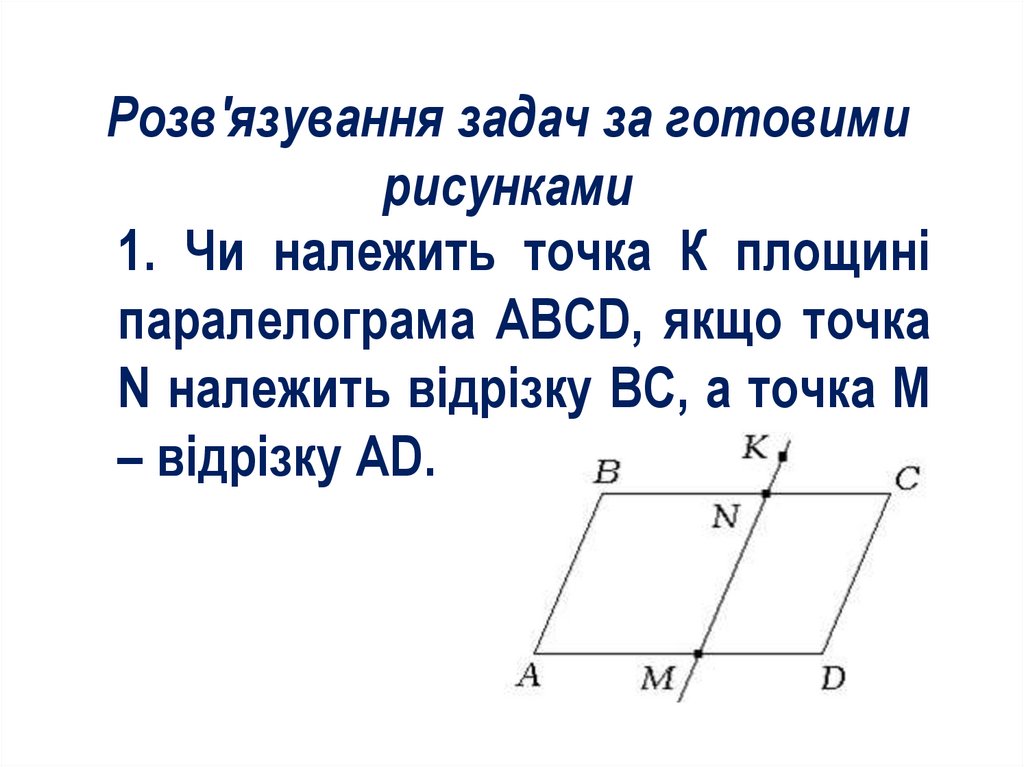
Розв'язування задач за готовими
рисунками
1. Чи належить точка К площині
паралелограма ABCD, якщо точка
N належить відрізку ВС, а точка M
– відрізку AD.

36.

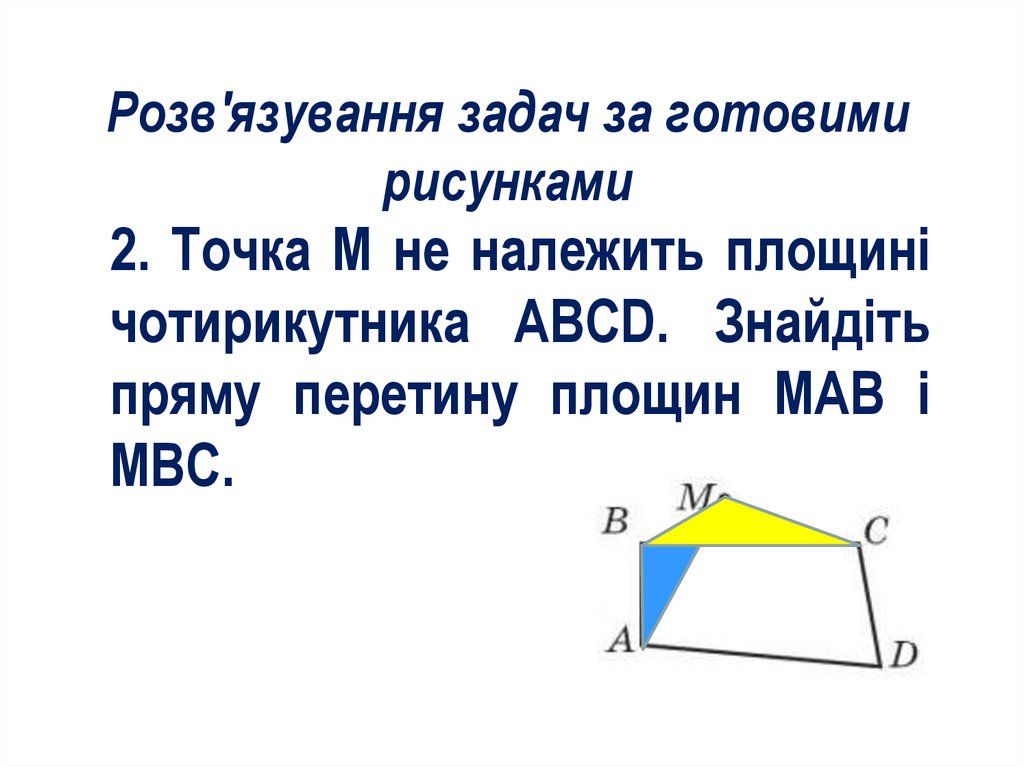
Розв'язування задач за готовими
рисунками
2. Точка М не належить площині
чотирикутника ABCD. Знайдіть
пряму перетину площин МАВ і
МВС.

37.

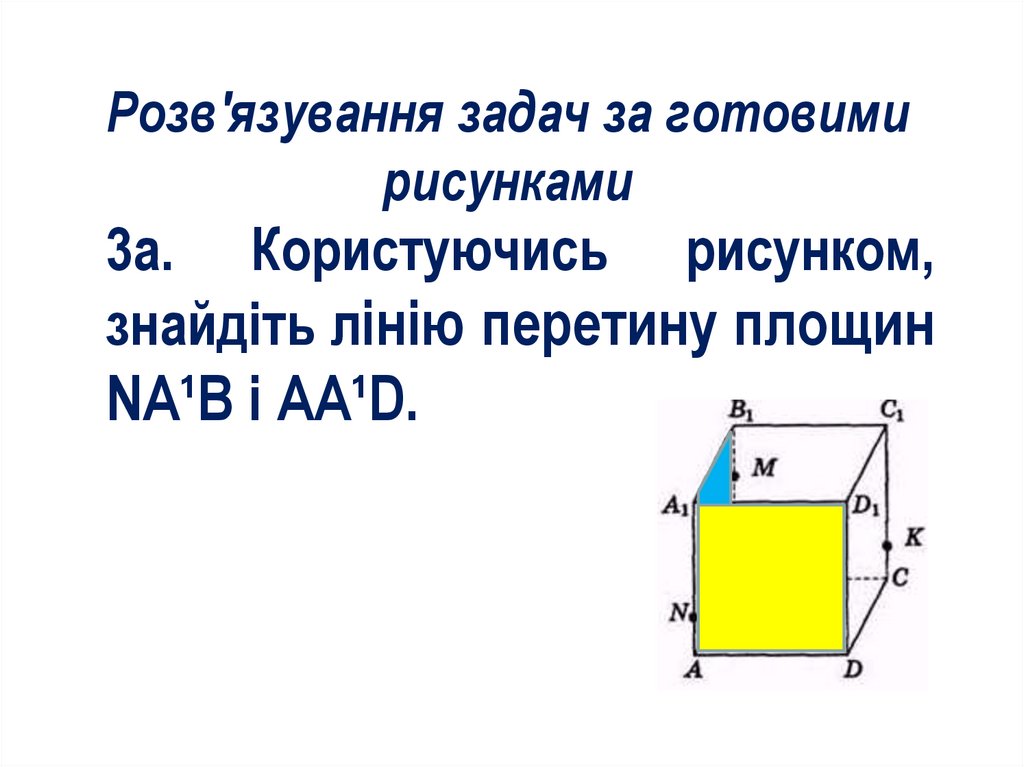
Розв'язування задач за готовими
рисунками
3а. Користуючись рисунком,
знайдіть лінію перетину площин
NА¹В і AA¹D.

38.

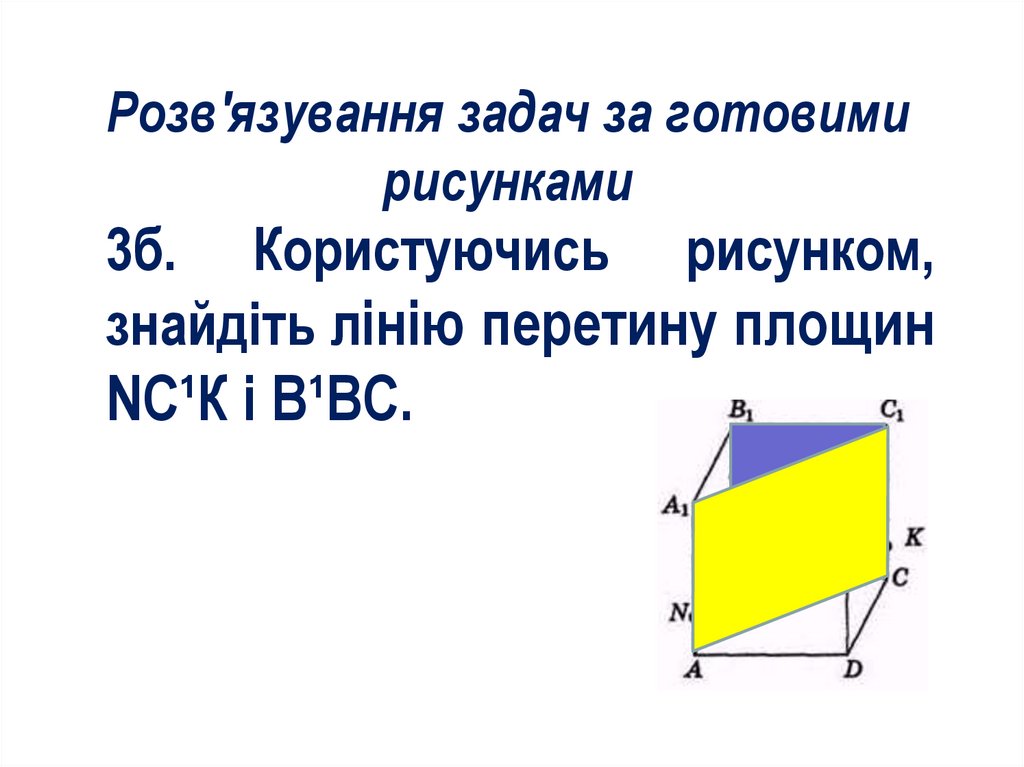
Розв'язування задач за готовими
рисунками
3б. Користуючись рисунком,
знайдіть лінію перетину площин
NС¹К і В¹ВС.

39.

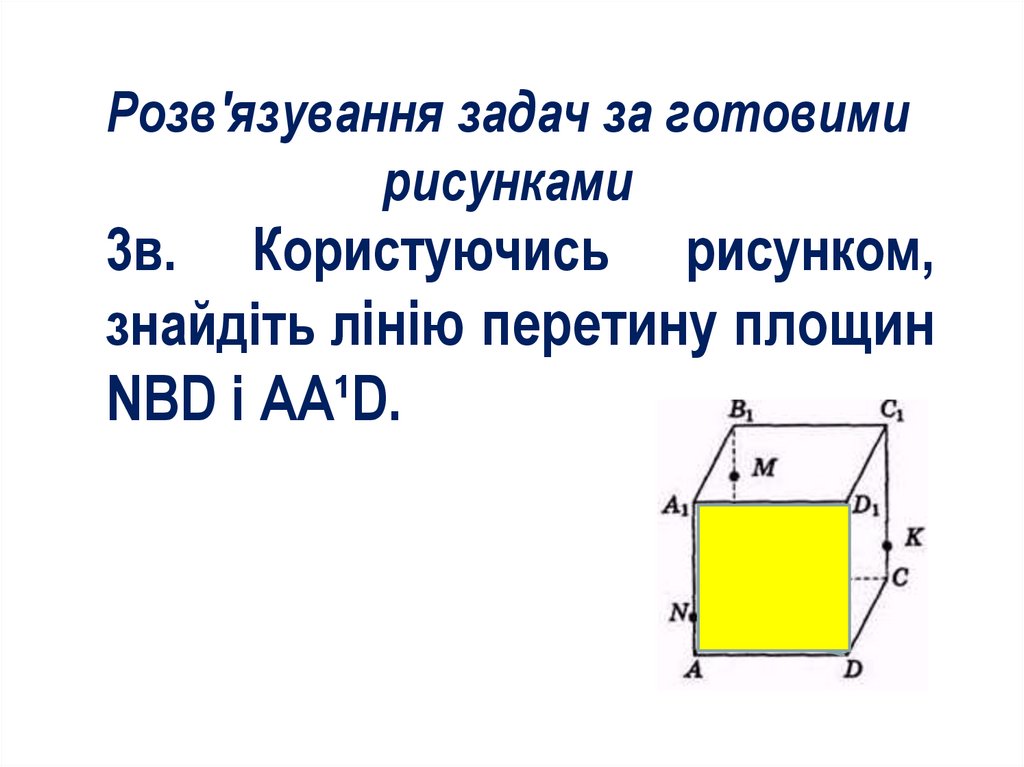
Розв'язування задач за готовими
рисунками
3в. Користуючись рисунком,
знайдіть лінію перетину площин
NBD і AA¹D.

40.

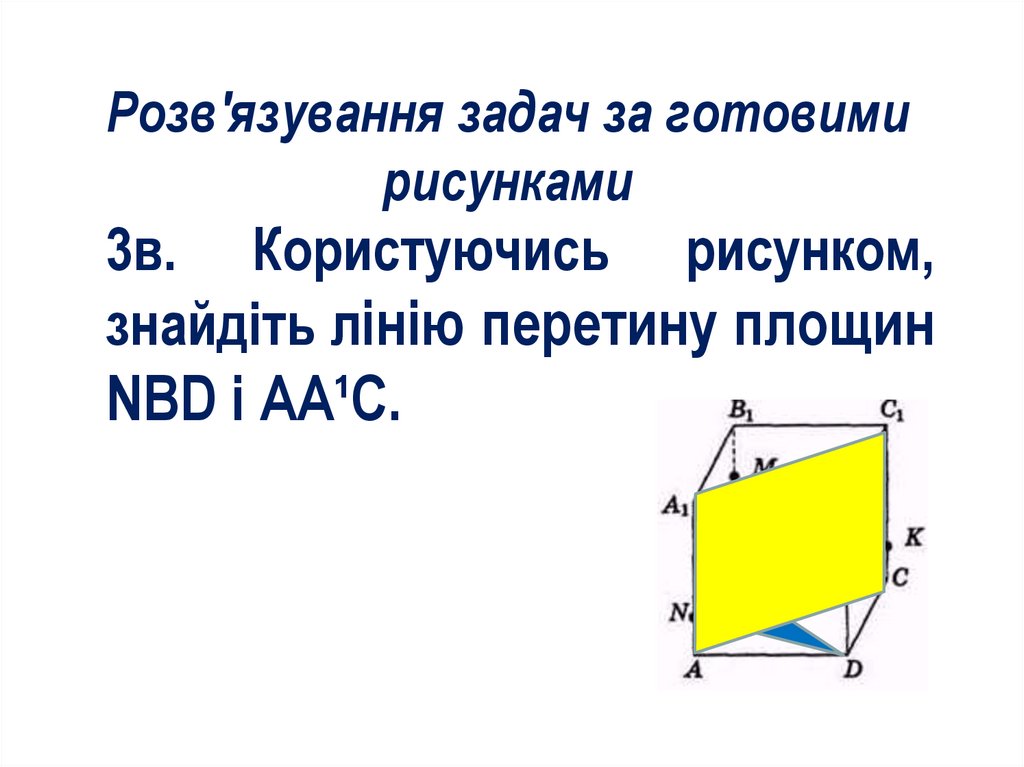
Розв'язування задач за готовими
рисунками
3в. Користуючись рисунком,
знайдіть лінію перетину площин
NBD і AA¹С.

41.

Додаткові завдання
1. Прямі АВ і АС перетинаються з
деякою прямою в точках М і N
відповідно. Доведіть, що точки
M, N, C, B лежать в одній
площині.

42.

Додаткові завдання
2. Скільки різних площин можна
провести через:
а) центр і діаметр кола;
б) центр і хорду кола?

43.

Тестові завдання

44.

Тестові завдання

45.

Домашнє завдання
1. Опрацювати § 1 ст. 224
2. Виконати тестові завдання
3. Виконати вправу 1.8, 1.12