Виды показательных уравнений и способы их решения

1. ВИДЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И СПОСОБЫ ИХ РЕШЕНИЯ

2. Цель занятия: Закрепление умений решать показательные уравнения

3.

Устный опрос
Повторение основных способов решения
показательных уравнений
Самостоятельная работа
Проверка самостоятельной работы
Домашнее задание
Подведение итогов

4. Считаем устно

1) Представить в виде степени:
3
6 ;
2
6
2
3
4
3 81;
0
3
2
2 16;
2
2
7 3 25
( )
5
49
7 1
( )
5

5. Решите уравнения

2x
3
3;
4
1 x
( ) 49;
7
5
x 1
0;
2
х 2
Корней
нет
Корней
нет
3 x
1;
х 3

6.

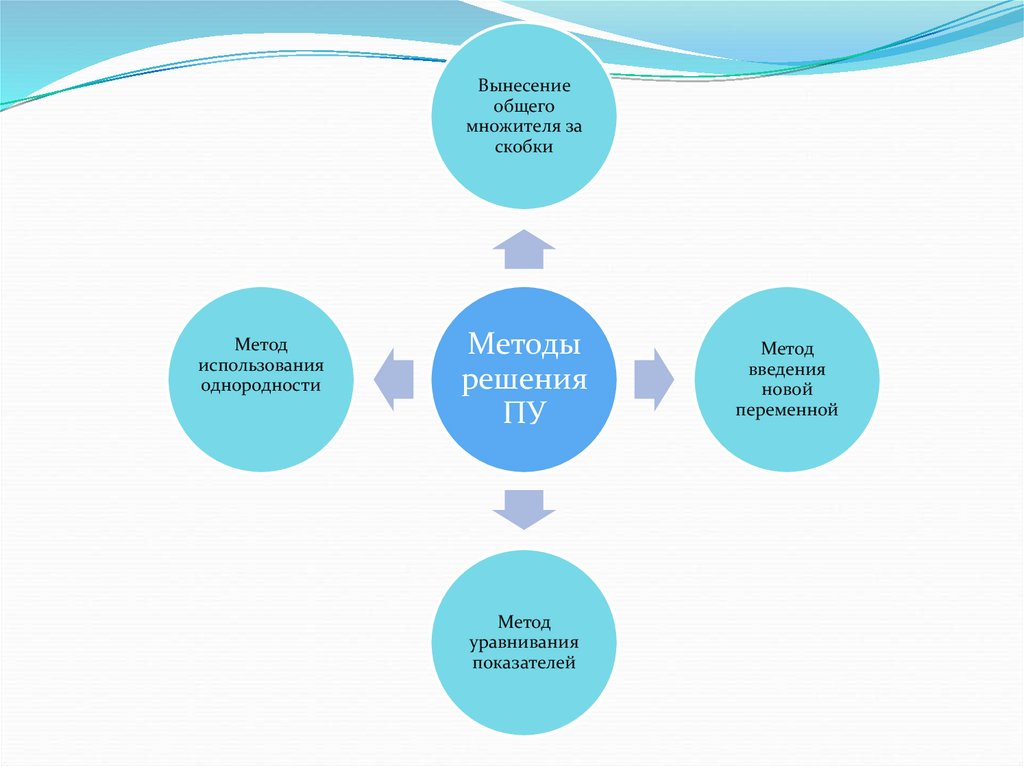
Вынесение
общего
множителя за
скобки
Метод
использования
однородности
Методы
решения
ПУ
Метод
уравнивания
показателей
Метод
введения
новой
переменной

7. Метод уравнивания показателей

1)5 5 , х 3
х
1)5
125
х
2) 2
3)3
3 х 6
х 1
4)8
х
2
3 х 6
1
2 ,3 х 6 1, х 2
3
1
3) Корней нет
3
х
4)8 8 , х 1, х 1
8
5 х 8
5)11
2)2
3
11
0
5 х 8
5)11
1
11 ,5 х 8 0, х 1,6
0

8. Вынесение общего множителя за скобки

x 2
3 72
x
2
3
x
3 (3 1) 72;
72
3 ;
8
x
3x 9;
3x 32;
x 2
Ответ: 2

9. Метод введения новой переменной

22
xx
11
xx
4 5 4 4 0
11
xx 22
11
xx
(4 ) 5 4 4 0;
11
xx
Пусть 44 tt,,tt 00..
Пусть
t 22 5t 4 0;
D 25 16 9;
44,,tt22
11..
tt11
ОДЗ :: x≠0
x≠0
ОДЗ
Вернемся кк
Вернемся
замене:
замене:
11
x1x1
11
4
4
4
4
xx
11
11
x
x
44 11
00
xx
xx 11
решений
нет
решений __ нет
Ответ: 1

10.

Решение:
4 x 2 x 1 3,
4 x 2 2 x 3 0,
x
y
2
. Уравнение
Сделаем
замену переменных. Пусть
1
у 2 2 y 3 0.
примет вид
Полученное уравнение имеет корни
2 x 3,
x
Сделаем обратную замену:
2
x
2 1
-3; 1
11 x 0 .
1
Ответ: 1

11.

Метод
введения новой переменной
9
x 2 1
36 3
2( x 2 1)
3
x 2 3
9 4 3
3 0
x 2 3
3 0;
Вернемся к
замене:
3x 1 3 x 2 1 1
2
2
x 1
3
1
x 1 0
2
Пусть 3x
2
1
t, t 0.
t 2 4t 3 0;
t1 3, t2 1.
x 0
x 0
x1 1
2
x 1 x 1
2
2
Ответ: 0,1,-1

12. Использование однородности

64 9 x 84 12 x 27 16 x 0
64 32 x 84 3x 4 x 27 4 2 x 0
Разделив обе части
уравнения на 4 2 x ,
получим:
3
3
64 ( )2 x 84 ( )x 27 0
4
4
3 x
(
) t, t 0.
Пусть
4
64t 84t 27 0;
2
t1
3
9
, t2 .
4
16
Вернемся к
замене:
3 x 3
( 4 ) 4
( 3 )x 9
4
16
x 1
x 2
Ответ: 1 или 2

13.

Самостоятельная работа
Решить уравнения:
1)5 х 1 1
2 х 1
2)3
3)0,5
27
х 2
16
4)2 х 3 2 х 28
5)4 х 6 2 х 8 0

14. Критерии оценки :

5 заданий
4 задания
3 задания
0-2 задания -
«5»
«4»
«3»
«2»

15. Ответы

1)
-1
2)
2
3)
-6
4)
5)
2
1;2

16. Умные мысли

Мне приходится делить время между политикой и
уравнениями.
Однако уравнения, по-моему, гораздо важнее.
Политика существует для данного момента, а
уравнения будут существовать вечно.

17.

Домашнее задание
1)5
2 x 3
25 ;
6х
12 x 1
2)3
3)5
2 x 1
9
6 x 1
27
4 5 4
x
2x
4 x 1
x 1
3 x 1
81
2192