Похожие презентации:
Outline. Basic de nitions (Lecture 1)
1.
OutlineBasic de nitions
1
Basic definitions
2
Main theorem
3
Euler method
4
Origin of DE
5
Standard forms of DE
6
H/w
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
2.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
Basic notations and de nitions
DEFINITION 1.
An ordinary differential equation is defined by an equality of the form
(1)
where the unknown function y also appears through its derivatives y(i), i = 1, ..., n. The
variable x is also called independent variable. The maximum order of differentiation of the
unknown function is called the order of the differential equation.
In the equation (1) x is single independent variable. In the case of several independent
variables, the derivatives are partial derivatives, and the equation is called a partial di erential
equation. We will consider only ordinary differential equations, and so the word ordinary will be
dropped. We will say di erential equations(DE).
H/w
3.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
It is considered that the variable x belongs to a real interval I, on which the function y is
de ned; this last one is supposed of class Cn(I), meaning that y is continuous on I, together with its
derivatives up to n th order inclusive. The interval I may be the following:
(α, β), [α, β), (α, β], [α, β], (α, ∞), [α, ∞), (−∞, β), (−∞, β], (−∞, ∞), where α, β ∈ R
and α < β.
DEFINITION 2.
A particular solution of (1) is a function of class Cn(I) that satisfies (1) for any x ∈ I. Every
particular solution y = y(x) is represented graphically by a curve in the (x, y)-plane, which is called
the integral (or solution) curve. The general solution (or general integral) of (1) is a
function
(2)
of class Cn(I), depending on n arbitrary constants C1, ..., Cn, corresponding to the order of
equation, and satisfying (1) on I, for any set of admissible constants.
4.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
DEFINITION 3.
It is said that the differential equation (1) is solved in quadratures if its general solution is
expressed through one or more integrals.
EXAMPLES.1. Let us consider the following DE
(3)
DE (3) is of first order. The function
is the general solution of (3), where C ∈ R. Indeed, we calculate
The function y(x) = x3 is a particular solution of the equation (3) and it can be obtained easily
by taking the particular value of C as 0 in the general solution.
5.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
2. The differential equation
(4)
has second order. The function
is the general solution of (4), where
I depend on the value of C1. It is easy to nd two derivatives of y(x) :
1
and
Note that the interval
6.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
It is interesting to note that y(x) = x2 is a solution of (4). Indeed 4x2 − 4x2 = 0. However, it is not
included in the general solution of (4). This "extra" solution, which cannot be obtained by
assigning particular values of the constants, is called a singular solution.
3. The equation
(5)
is solved in quadratures. Indeed, the general solution of (5) is the following function
where C is an arbitrary constant.
4. In the equation
ut(x, t) = uxx(x, t)
(6)
derivatives,
the equationvariables,
(6) is partial
erential function.
equation Since
of second
order.
Moreover,
x and t are independent
u is di
unknown
ut and
uxx are
partial (6) is
well known heat equation.
7.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
A DE of the first order may be written as
(7)
DEFINITION 4.
The function y = ϕ(x) is called an explicit solution of (7) provided
(8)
A relation of the form ψ(x, y) = 0 is said to be an implicit solution of (7) provided it
determines one or more functions y = ϕ(x) which satisfy (8).
It is frequently difficult, if not impossible, to solve ψ(x, y) = 0 for y. Nevertheless, we can test the
solution by obtaining
by implicit differentiation:
and check if
F (x, y, −ψx/ψy ) ≡ 0 in I.
Both explicit solutions and implicit solutions will usually be called simply solutions.
8.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
EXAMPLE.It is easy to check that the following DE of the rst order
(9)
has the implicit solution x2 + y2 = C, C > 0. Indeed, differentiating last equality by x we
obtain:
The pair of functions x = x(t), y = y(t) is said to be a parametric solution of
when
.
EXAMPLE.Let us consider the equation (9). Then the pair of functions x = C sin t,
y = C cos t, (C ∈ R, C ƒ= 0, t ƒ= π/2 + πn, n ∈ Z) is a parametric solution of (9). Since
9.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
Some differential equations may be developed with respect to y(n) to give
(10)
We call this form normal. Most equations will be considered in normal form.
Differential equations are classified into two groups: linear and nonlinear. A DE is said to be
linear if it is linear in y and all its derivatives. Thus, an n-th order linear DE has the form
(11)
DEFINITION 5.
In (11) if the function f (x) ≡ 0, then it is called a homogeneous DE, otherwise it is said to be
a nonhomogeneous DE. An equation that is not of the form (11) is a nonlinear DE.
Obviously, (3) is linear nonhomogeneous DE, whereas (4) is nonlinear homogeneous DE.
10.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
In applications we are usually interested in a solution of the DE (10) satisfying some additional
requirements called initial or boundary conditions.
DEFINITION 6.
By initial conditions for (10) we mean n conditions of the form
(12)
where y0, ..., yn−1 and x0 are given constants. A problem consisting of the DE (10) together
with the initial conditions (12) is called an initial value problem or the Cauchy problem.
It is common to seek a solution y(x) of the initial value problem (10), (12) in an interval I
which contains the point x0.
11.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
DEFINITION 7.
If the conditions relate to two different x values, the problem is called a two-point
boundary-value problem(or simply a boundary-value problem).
We formulate two-point conditions for the n-th order DE (10):
where y(0) = y and αij, βij, γi, i, j = 0, n − 1 are given constants and a, b ∈ I.
It is well known boundary-value problems is Sturm Liouville problems. Let us consider one of
them:
H/w
12.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
EXAMPLES.
1) Consider the problem
Both of initial conditions relate to one x value, namely, x = 1. Thus this is an initial-value
problem. We will see later that this problem has a unique solution.
2) Consider the problem
In this problem we again seek a solution of the same di erential equation, but the conditions
relate to the two di erent x values, 0 and π/2. This is a (two-point) boundary-value problem.
This problem also has a unique solution; but the boundary-value problem
has no solution at all! This simple fact may lead one to the correct conclusion that
boundary-value problems are not to be taken lightly!
Alexander Gladkov, Professor
DIFFERENTIAL EQUATIONS
Belarusian State University
13.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
DEFINITION 8.
An equilibrium solution of differential equation is a solution whose derivative is zero
everywhere.
EXAMPLE.
Find the equilibrium solutions of the differential equation son
The differential equation above can be rewritten as
Therefore y(x) ≡ −3 and y(x) ≡ 3 are the equilibrium solutions.
Alexander Gladkov, Professor
DIFFERENTIAL EQUATIONS
Belarusian State University
14.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
THEOREM. (Existence and uniqueness theorem)
Consider the initial value problem
(13)
(14)
Let D be a domain in Rn+1, (x0, y0, ..., yn−1) ∈ D, f (x, y1, y2, ..., yn) ∈ C(D) and
∂f/∂yi ∈ C(D) for i = 1, ..., n. Then there exists a unique solution of (13, (14), de ned on some
interval |x − x0| < h, where h is sufficiently small.
The proof of this theorem is omitted.
Alexander Gladkov, Professor
DIFFERENTIAL EQUATIONS
Belarusian State University
15.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
EXAMPLE.
Consider the initial value problem
(15)
Right-hand side of DE in (15) f (x, y) = 3y2/3 is continuous function in D = R2. It is easy to check
that y = (x + C)3, C ∈ R is the general solution of (15) on the interval I = R :
Calculating ∂f/∂y = 2y−1/3/3, we obtain that ∂f/∂y is continuous function if y ƒ= 0. Let
Then
point (x0, y0).
is the unique solution of (15) in some neighborhood of
16.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
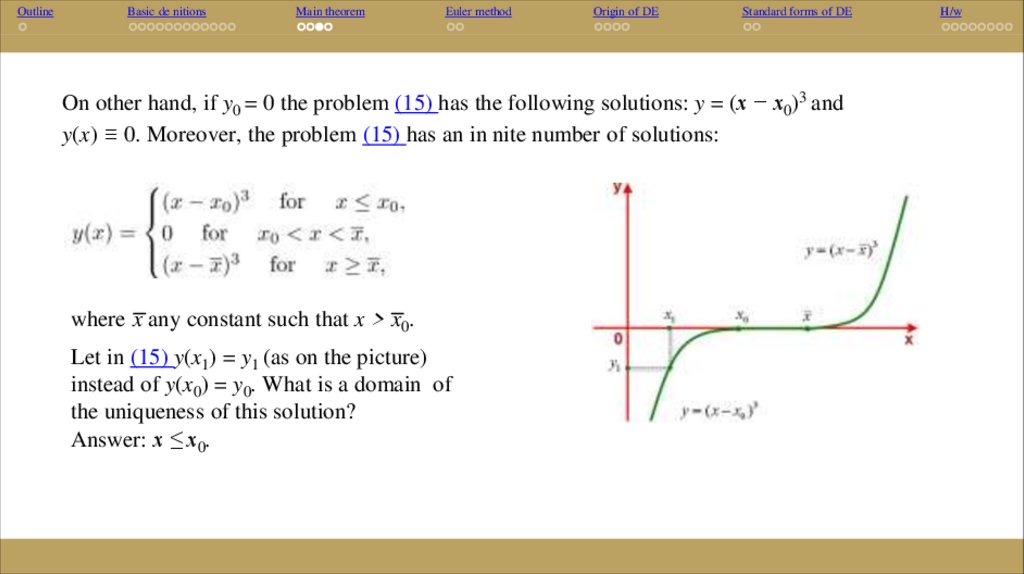
On other hand, if y0 = 0 the problem (15) has the following solutions: y = (x − x0)3 and
y(x) ≡ 0. Moreover, the problem (15) has an in nite number of solutions:
where x any constant such that x > x0.
Let in (15) y(x1) = y1 (as on the picture)
instead of y(x0) = y0. What is a domain of
the uniqueness of this solution?
Answer: x ≤ x0.
H/w
17.
OutlineBasic de nitions
Main theorem
Euler method
Note that Existence and uniqueness
theorem states the existence of unique
solution only in some small interval.
Let us consider the following initial value
problem
(16)
All conditions of the theorem are satis ed.
It is easy to check that y(x) = (1 − x)−1 is a
solution of (16):
and y(x) exists only for x < 1.
Origin of DE
Standard forms of DE
H/w
18.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
The Euler method
Although it is not always possible to nd an analytical solution of
(17)
for y = y(x), it is always possible to determine a numerical solution given an initial value y(x0) =
y0, provided f (x, y) is a well-behaved function. The di erential equation (17) gives us the slope f
(x0, y0) of the tangent line to the solution curve y = y(x) at the point (x0, y0).
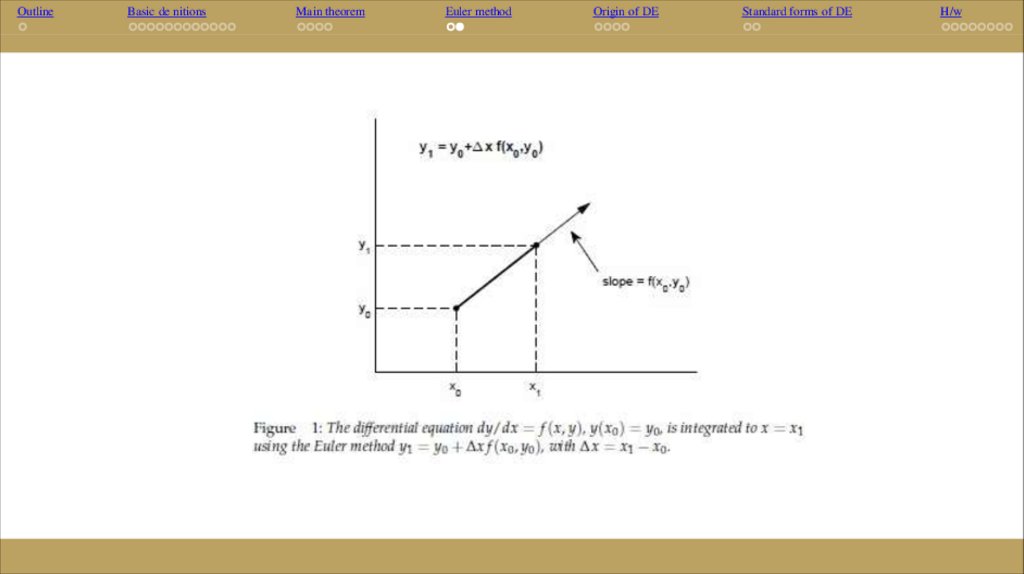
With a small step size ∆x = x1 − x0, the initial condition (x0, y0) can be marched forward to
(x1, y1) along the tangent line using Euler's method (see Fig. 1)
y1 = y0 + ∆x f (x0, y0).
Now (x1, y1) becomes the new initial condition and is marched forward to (x2, y2) along a
newly determined tangent line with slope given by f (x1, y1) :
y2 = y1 + ∆x f (x1, y1).
For small enough ∆x, the numerical solution converges to the exact solution.
19.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
20.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
Origin and applications of di erential equations
The laws of the universe are written in the language of mathematics. Algebra is su cient to
solve many static problems, but the most interesting natural phenomena involve change and are
described by equations that relate changing quantities.
Because the derivative
of the function f is the rate at which the quantity
y = f (t) is changing with respect to the independent variable t, it is natural that equations
involving derivatives are frequently used to describe the changing universe.
EXAMPLES.
1). As rst example, consider a mass falling under the in uence of constant gravity, such as
approximately found on the Earth's surface. Newton's law, F = ma, results in the equation
where y is the height of the object above the ground, m is the mass of the object, and
g ≈ 9.8meter/sec2 is the constant gravitational acceleration.
H/w
21.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
The mass cancels from the equation, and
Here, the right-hand-side of the DE is a constant. The rst integration yields
with A the rst constant of integration. The second integration yields
with B the second constant of integration. The two constants of integration A and B can then be
determined from the initial conditions. If we know that the initial height of the mass is y0, and the
initial velocity is v0, then the initial conditions are
22.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
Substitution of these initial conditions into the equations for dy/dt and y allows us to solve for
A and B :
The unique solution that satis es both DE and the initial conditions is given by
(18)
For example, suppose we drop a ball from the top of a 50 meter building. How long will it take the
ball to hit the ground? This question requires solution of (18) for the time T it takes for y(T ) = 0,
given y0 = 50 meter and v0 = 0. Solving for T,
23.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
2). Newton's law of cooling may be stated in this way: The time rate of change (the rate of
change with respect to time t) of the temperature T (t) of a body is proportional to the
difference between T and the temperature A of the surrounding medium. That is,
dT
= −k(T − A),
dt
where k is a positive constant. Observe that if T > A, then
, so the temperature is a
decreasing function of t and the body is cooling. But if T < A, then
, so that T is
increasing. Thus the physical law is translated into a di erential equation. If we are given the
values of k and A, initial temperature T (0) = T0, we are able to predict the future temperature of
the body by explicit formula:
T (t) = A + (T0 − A) exp(−kt).
Indeed,
dT
= −k(T0 − A) exp(−kt) = −k [A + (T0 − A) exp(−kt) − A] = −k(T − A).
dt
Obviously, T (t) → A as t → ∞.
H/w
24.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
Standard forms of rst-order DE
The first-order differential equations to be studied may be expressed in either the normal form
dy
= f (x, y)
dx
(19)
or the differential form
M (x, y)dx + N (x, y)dy = 0.
(20)
An equation in one of these forms may readily
dy be written in the other form. For example, the
=
equation
dx2
x − y2
is of the form (19). It may be written
x2 + y2
(x2 + y2)dy + (y2 − x2)dx = 0,
which is of the form (20).
H/w
25.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
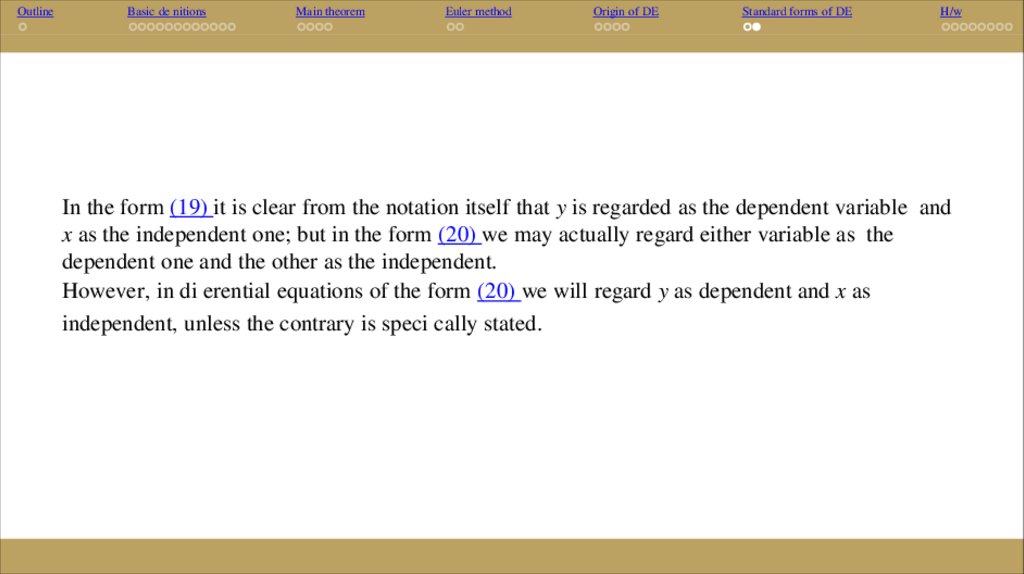
In the form (19) it is clear from the notation itself that y is regarded as the dependent variable and
x as the independent one; but in the form (20) we may actually regard either variable as the
dependent one and the other as the independent.
However, in di erential equations of the form (20) we will regard y as dependent and x as
independent, unless the contrary is speci cally stated.
26.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
Homework
We will use the following books:
1. S.L. Ross, Differential equations, Wiley, 1984.
2. C. Constanda, Differential equations, Springer, 2017
3. M.V. Soare, P.P. Teodorescu and I. Toma, Ordinary differential equations with applications
to mechanics, Springer, 2007.
4. M. V. Makarets, V. Yu. Reshetnyak, Ordinary differential equations and calculus of
variations, World Scienti c Publishing, 1995.
E. A. Coddington, An introduction to ordinary differential equations, Dover Publications, 1989.
For reading:
PDF presentation,
S.L. Ross. PP. 1 24.
H/w
27.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
Problems
I. Classify each of the following di erential equations as ordinary or partial di erential
equations; state the order of each equation; and determine whether the equation under
consideration is linear or nonlinear:
II. Show that 5x2y2 − 2x3y2 = 1 is an implicit solution of the differential equation
H/w
28.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
III. Show that every function f de ned by f (x) = (x3 + c) exp(−3x), where c is an arbitrary
constant, is a solution of the di erential equation
IV. For certain values of the constant m the function f de ned by f (x) = exp(mx) is a
solution of the di erential equation
Determine all such values of m.
V. Show that the function f de ned by f (x) = 3 exp(2x) − 2x exp(2x) − cos(2x) satis es the
differential equation
and also the conditions that
H/w
29.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
Extra materials
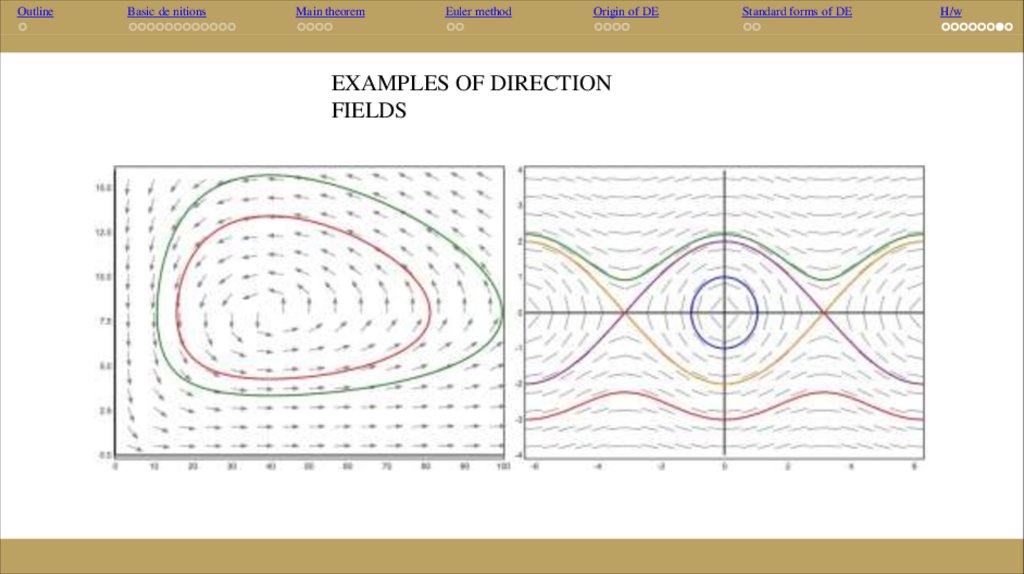
Direction fields
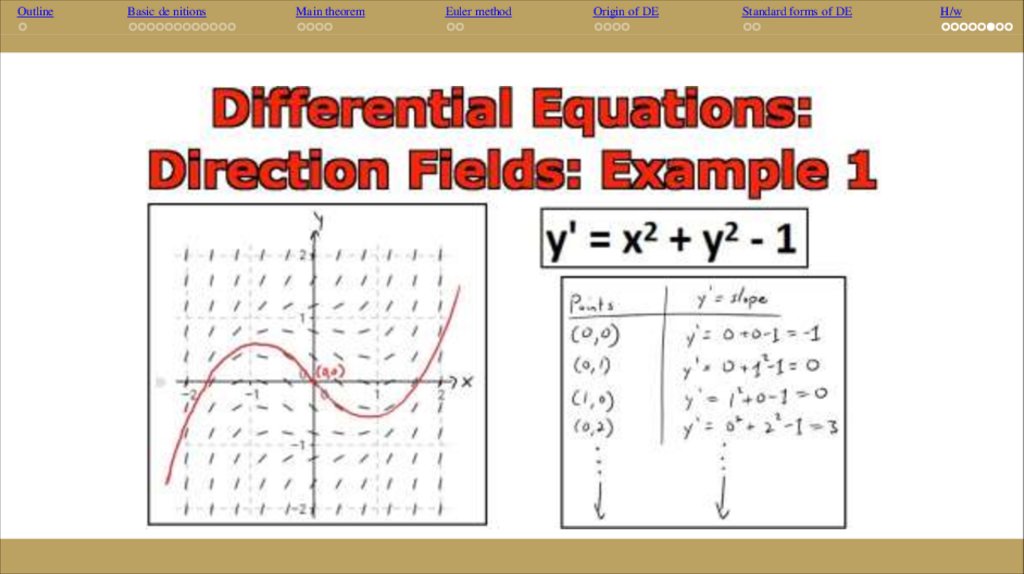
Very often, a nonlinear first-order DE cannot be solved by means of integrals; therefore, to
obtain information about the behavior of its solutions we must resort to qualitative analysis
methods. One such technique is the sketching of so-called direction elds, based on the fact
that the right-hand side of the equation
is the slope of the tangent to the solution
curve y = y(x) at a point (x, y). Drawing short segments of the line with slope f (x, y) at each node
of a suitably chosen lattice in the (x, y)-plane, and examining the pattern formed by these
segments, we can build up a useful pictorial image of the family of solution curves of the given
DE.
30.
OutlineBasic de nitions
Alexander Gladkov, Professor
DIFFERENTIAL EQUATIONS
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
Belarusian State University
31.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
Standard forms of DE
H/w
32.
OutlineBasic de nitions
Main theorem
Euler method
Origin of DE
EXAMPLES OF DIRECTION
FIELDS
Standard forms of DE
H/w
33.
OutlineBasic de nitions
Main theorem
Euler method
Extra homework
For reading:
PDF presentation,
C. Constanda. PP. 41 42.
Problems
I. Construct other solutions of problem (15) with y0 = 0.
I. Draw the direction eld for DE
Origin of DE
Standard forms of DE
H/w




























 Математика
Математика








