Descriptive statistics (chapter 2)

1.

CHAPTER 2
STATISTICS FOR BUSINESS AND ECONOMICS 13e Anderson,
David R 2017

2.

Descriptive statistics
CATEGORICAL
VARIABLE
QUANTITATIVE
VARIABLE
TWO VARIABLES
TWO VARIABLES USING
GRAPHICAL DISLPAY

3.

Statistics in Practice
■ 38,000 employees
■ Represented in more than 200 countries
■ Uses statistics in its quality assurance program
■ For example: customer satisfaction with the quantity of detergent in a carton

4.

Statistics in Practice
■ Every carton in each size category is filled with the same amount of detergent by
weight, but the volume of detergent is affected by the density of the detergent
powder
– For example, if powder density is on the heavy side, smaller volume of
detergent may be needed, therefore carton may appear under filled
■ Limits are placed on the acceptable range of powder density
■ Statistical samples are taken periodically, and the density of each powder sample is
measured
■ Following data has been uncovered:

5.

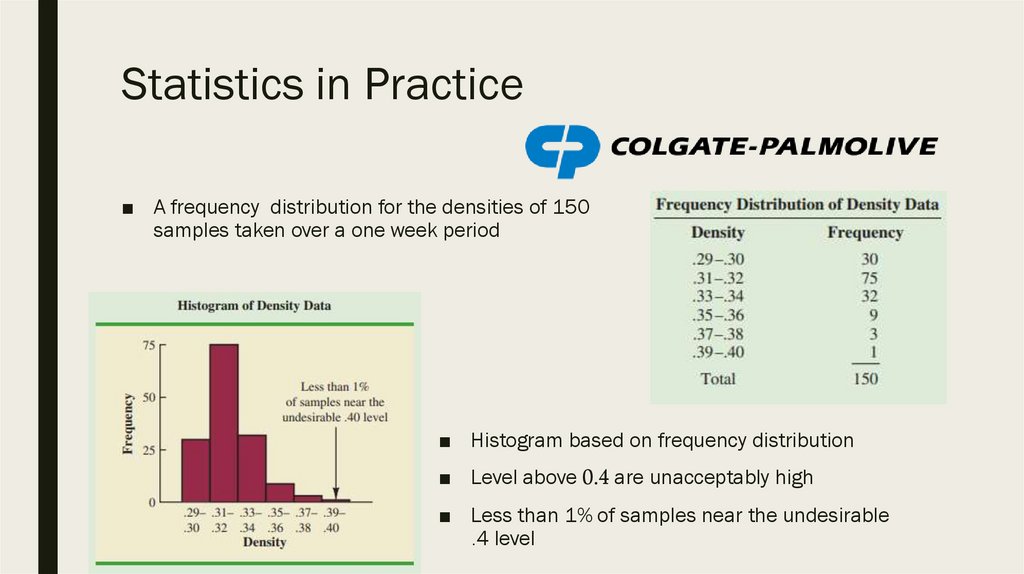
Statistics in Practice
■ A frequency distribution for the densities of 150
samples taken over a one week period
■ Histogram based on frequency distribution
■ Level above 0.4 are unacceptably high
■ Less than 1% of samples near the undesirable
.4 level

6.

Statistics in Practice
■ In this chapter we will learn tabular and graphical methods of descriptive statistics
■ Such as
–
–
–
–
–
Frequency distribution
Bar charts
Histograms
Stem-and-leaf displays
Crosstabulations

7.

Introduction
■ Before discussing descriptive statistics, lets learn statistical terms used

8.

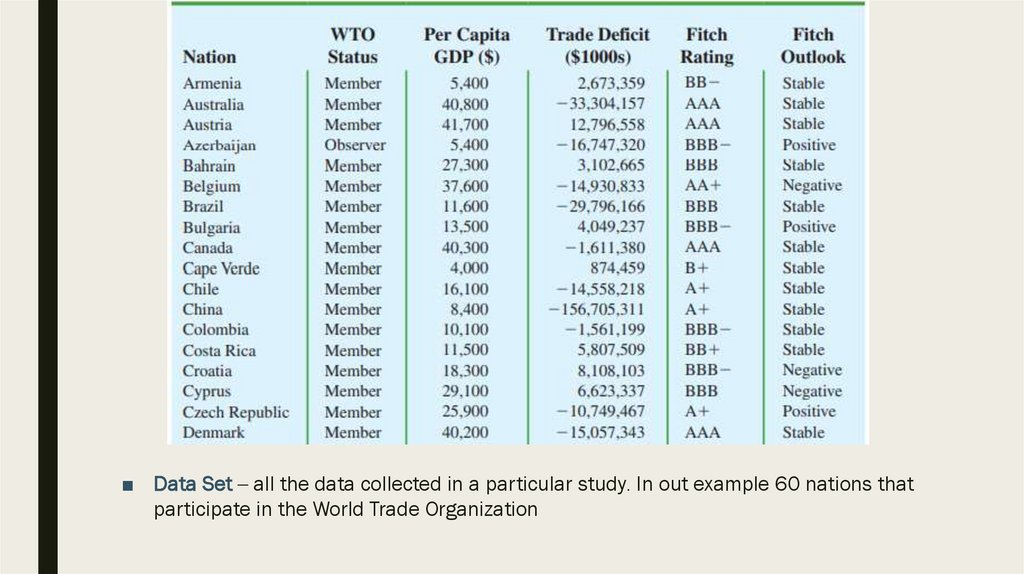
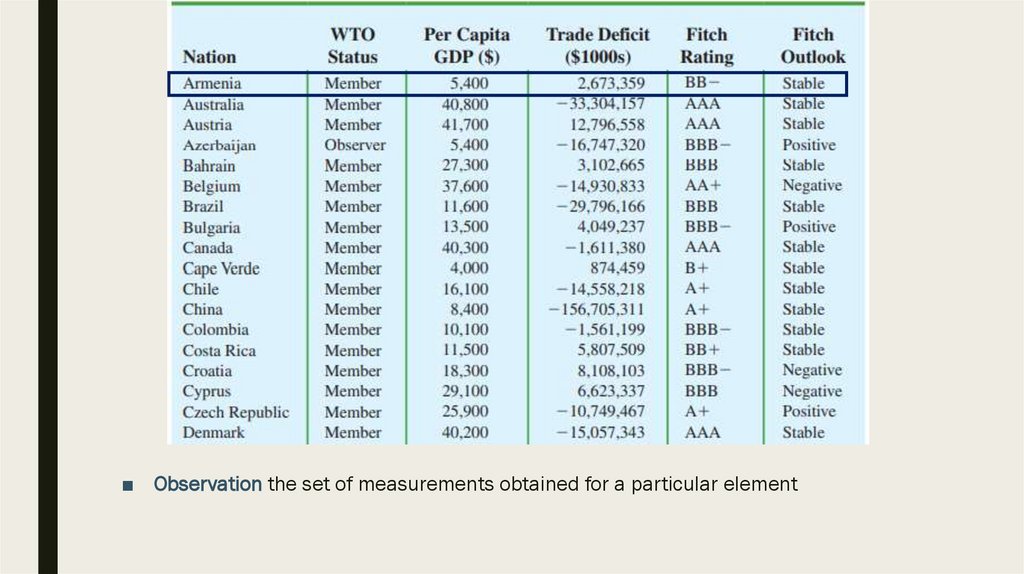
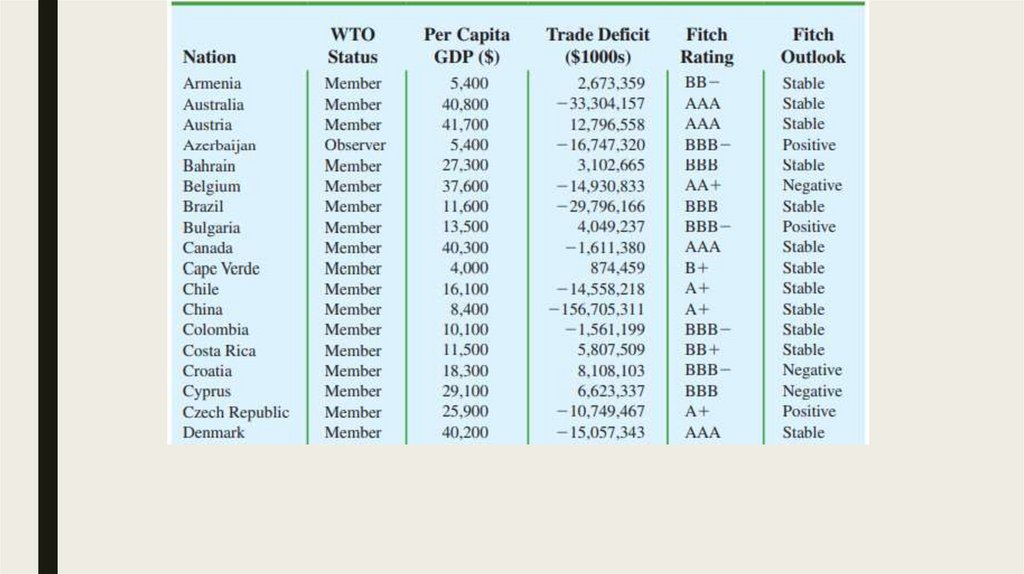
■ Data Set – all the data collected in a particular study. In out example 60 nations that
participate in the World Trade Organization

9.

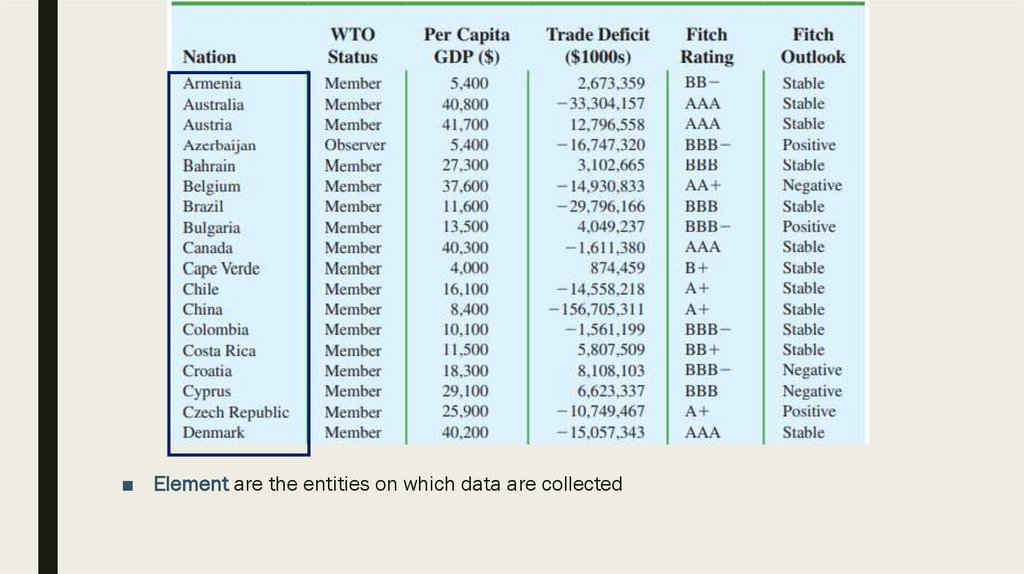
■ Element are the entities on which data are collected

10.

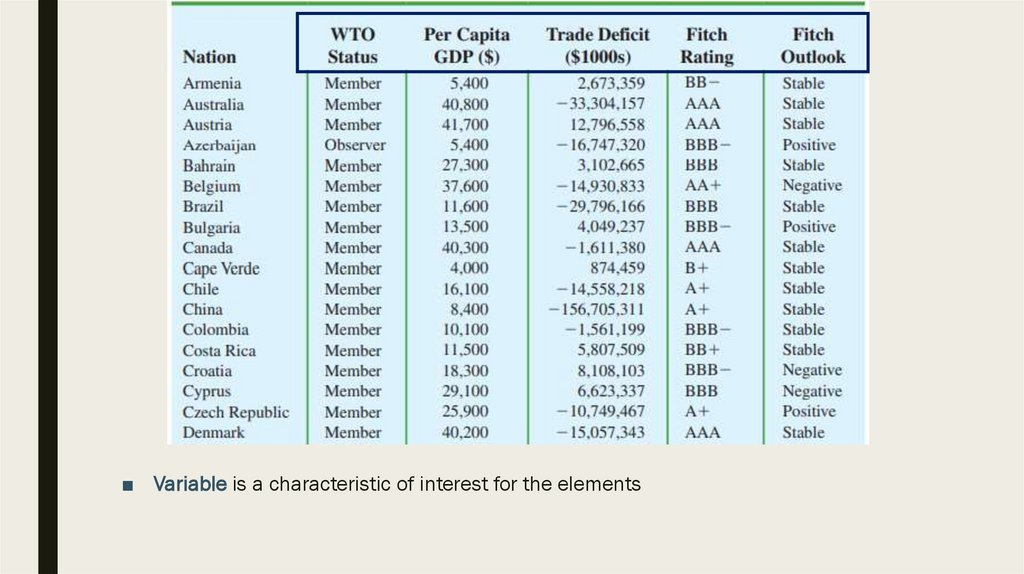
■ Variable is a characteristic of interest for the elements

11.

■ Observation the set of measurements obtained for a particular element

12.

Introduction
■ Variable scales of measurement
– Nominal – consists of labels or names used to identify an attribute of the
element
– Ordinal – exhibits the properties of nominal data and in addition, the order or
rank of the data is meaningful
– Interval – has all the properties of ordinal data and the interval between values
is expressed in terms of a fixed unit of measure (always numerical)
– Ratio – has all properties of interval data and the ratio of two values is
meaningful
■ Let’s observe our data

13.

14.

Introduction
■ Data classification:
■ Categorical Data
– Can be grouped by specific categories
– Can be either nominal or ordinal scale of measurement
■ Quantitative Data
– Variable with quantitative data (answers question how many)
– Can be either interval or rational scale

15.

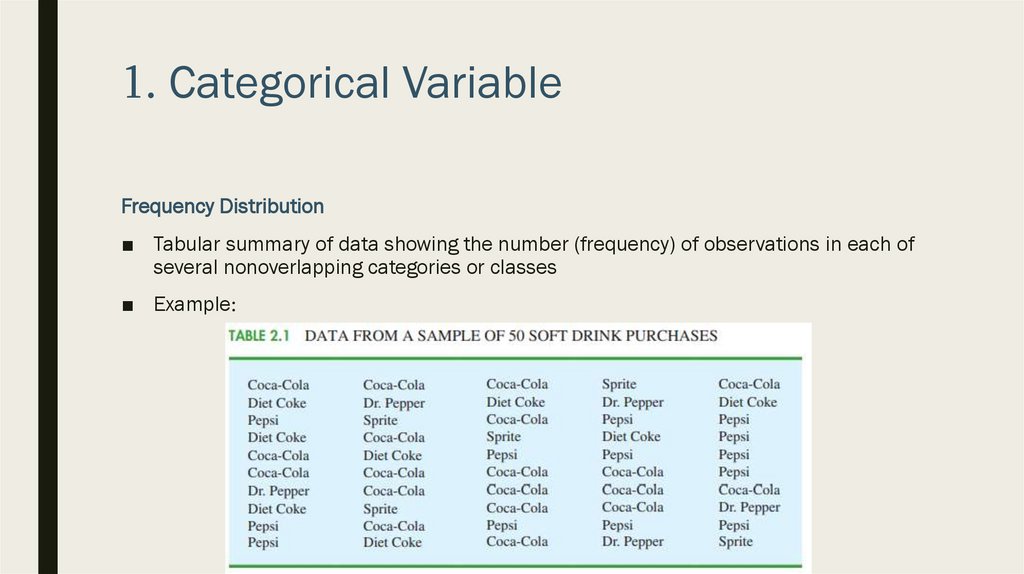
1. Categorical Variable
Frequency Distribution
■ Tabular summary of data showing the number (frequency) of observations in each of
several nonoverlapping categories or classes
■ Example:

16.

1. Categorical Variable
Frequency Distribution
■ To develop a frequency distribution for these data, we count the number of times
each soft drink appears in each class

17.

1. Categorical Variable
Relative Frequency Distribution
■ Displays proportion, or percentage, of observations in each class
■ Relative frequency of a class equals the fraction or proportion of observations
belonging to a class

18.

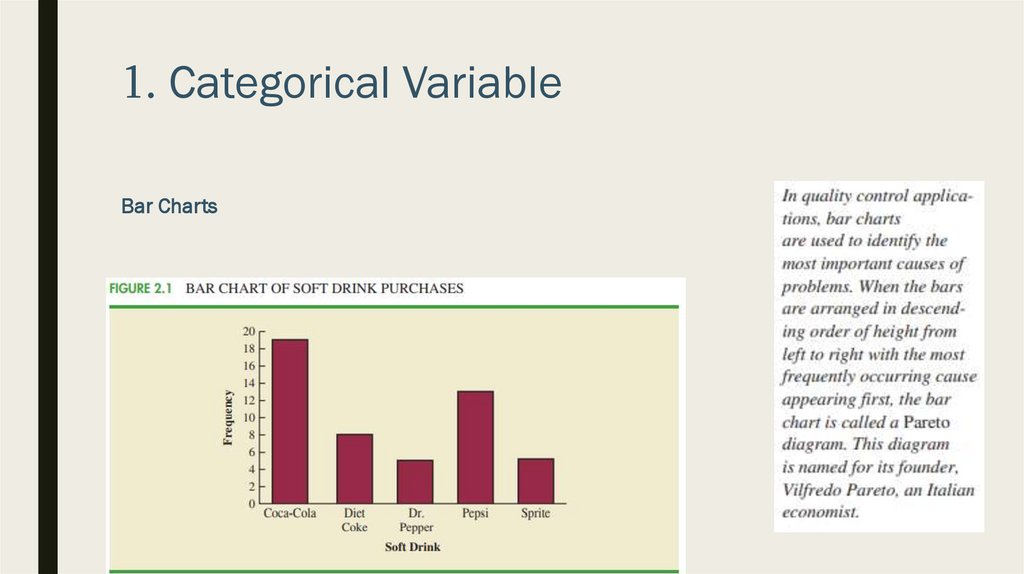
1. Categorical Variable
Bar Charts
■ Graphical display for depicting categorical data summarized in a frequency, relative
frequency, or percent frequency distribution
■ Let’s display Bar Chart for our example:

19.

1. Categorical Variable
Bar Charts

20.

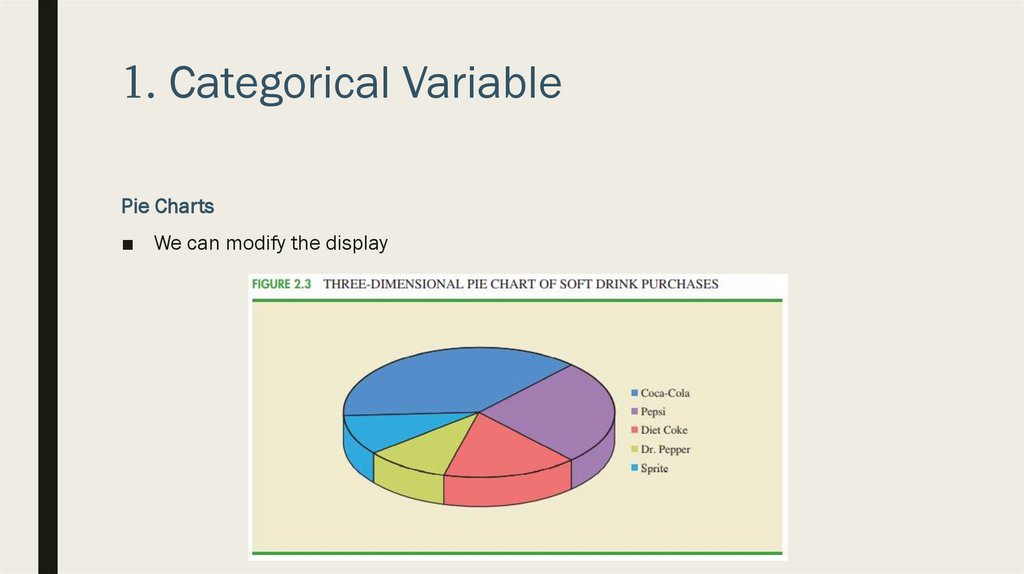
1. Categorical Variable
Pie Charts
■ Another graphical display for
presenting relative frequency and
percent frequency distributions for
categorical data
■ In our example:

21.

1. Categorical Variable
Pie Charts
■ We can modify the display

22.

2. Quantitative Variable
Frequency Distribution
■ In this case we have numbers
■ Biggest challenge, determining class boundaries
■ Three necessary steps:
1. Determine the number of nonoverlapping classes
2. Determine the width of each class
3. Determine the class limits
■ Let’s determine boundaries using our example

23.

2. Quantitative Variable
Frequency Distribution
(1) Determine the number of nonverlapping classes
■ General guideline, use between 5 and 20 classes
■ The goal is to use enough classes to show the variation in the data, but not so many
classes that some contain only a few data items

24.

2. Quantitative Variable
Frequency Distribution
(2) Determine the width of each class
■ As a general guideline, the width be the same for each class
■ Generally we use formula:

25.

2. Quantitative Variable
Frequency Distribution
■ In our example
■ Let’s use 5 classes
■ Therefore:
– Largest data value is 33
– Lowest data value is 2
■ Category width is (33-12)/5=4.2
■ Let’s round up and say 5

26.

2. Quantitative Variable
Frequency Distribution
(3) Determine the class limits
■ Must be chosen so that each data item belongs to one and
only one class
■ For example:

27.

2. Quantitative Variable
Frequency Distribution
(3) Determine the class limits
■ We can display it using relative frequency distribution

28.

2. Quantitative Variable
Frequency Distribution
Class midpoint
■ In some cases, we may want to know the midpoints of each lasses in a frequency
distribution
■ In our case: 12, 17, 22, 27 and 32

29.

2. Quantitative Variable
Relative Frequency Distribution
■ To display relative frequency per class:
■ It will show us frequency or percentage distribution for quantitative data in each
class
■ In our example, we have 20 data points
■ For 15-19 class, we have 8 data points, therefore 8/20=.40 or 40%

30.

2. Quantitative Variable
Dot Plot
■ Simplest graphical summaries of data
■ Example:

31.

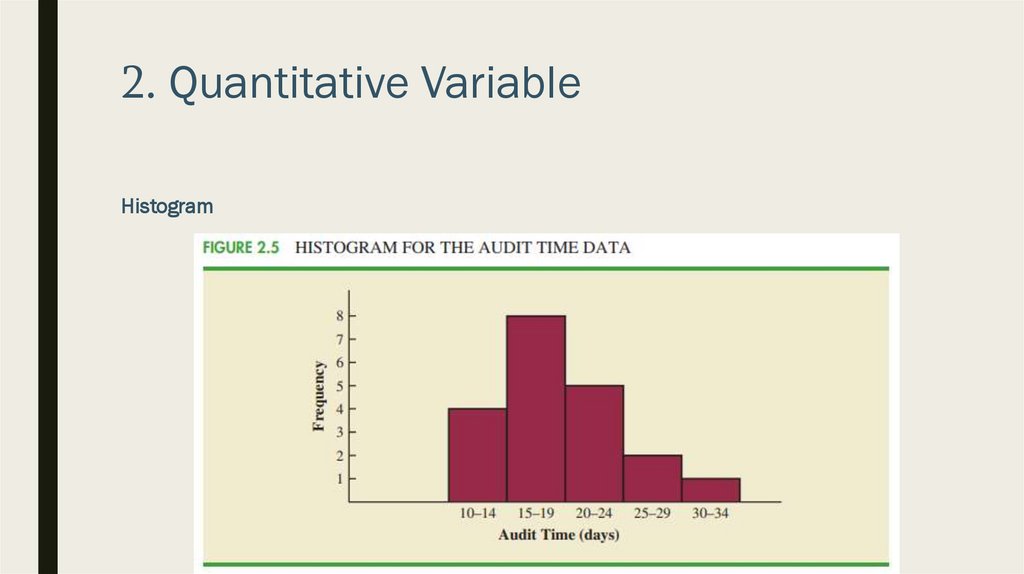
2. Quantitative Variable
Histogram
■ Most commonly used graphical display of quantitative data
■ Can be prepared using data in either a frequency, relative frequency or percent
frequency distribution
■ A histogram is constructed by placing the variable of interest on the horizontal axis
and the frequency, relative frequency, or percent frequency on the vertical axis
■ Frequency, relative frequency, or percent frequency is shown by drawing a rectangle
whose base is determine by the class limits on the horizontal axis and whose height
is the corresponding frequency, relative frequency, or percent frequency
■ Example:

32.

2. Quantitative Variable
Histogram

33.

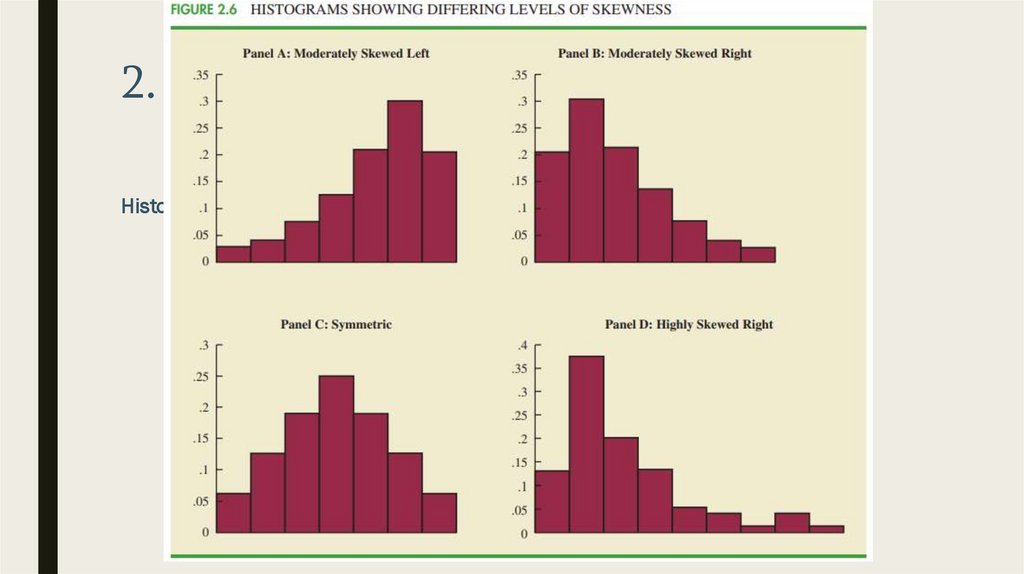
2. Quantitative Variable
Histogram
■ One of the most important uses of histogram is to provide information about the
shape or form of a distribution
■ Example:

34.

2. Quantitative Variable
Histogram

35.

2. Quantitative Variable
Cumulative Distribution
■ Variation of the frequency distribution
■ Uses same number of classes, class widths, and class limits developed for the
frequency distribution
■ However, rather than showing the frequency of each class, the cumulative frequency
distribution shows the number of data items with values les than or equal to the
upper class limit of each class
■ Example

36.

2. Quantitative Variable
Cumulative Distribution

37.

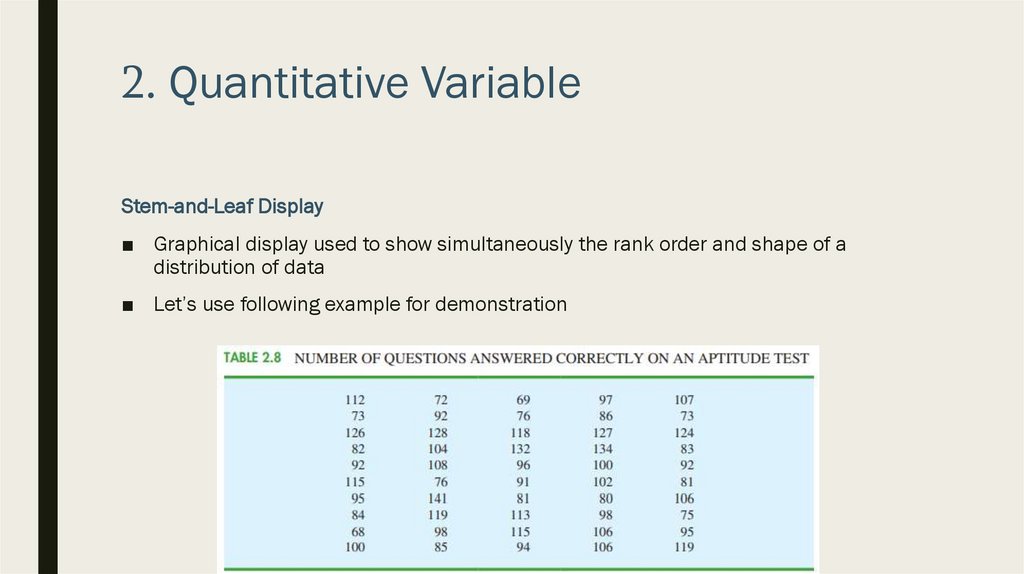
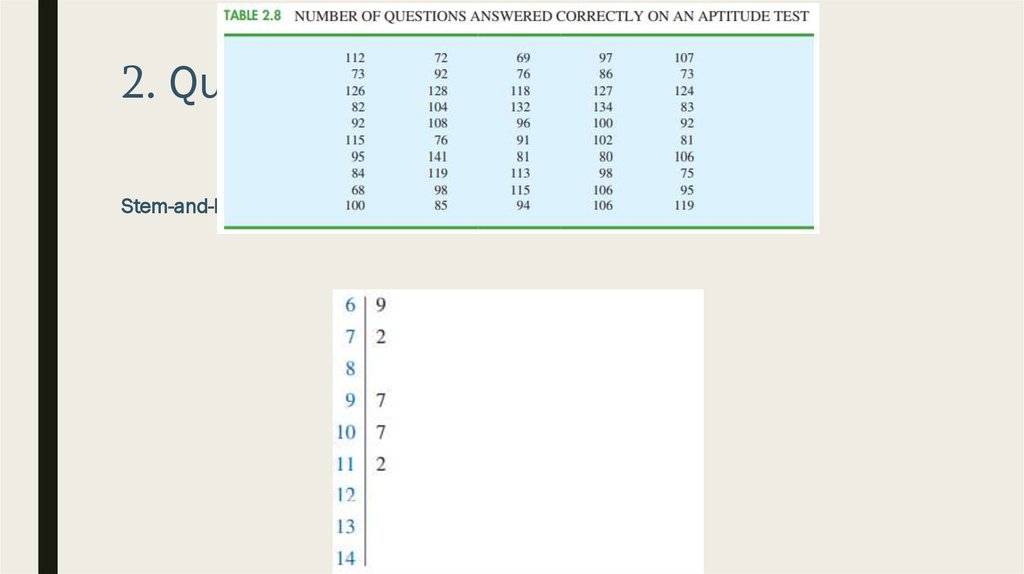
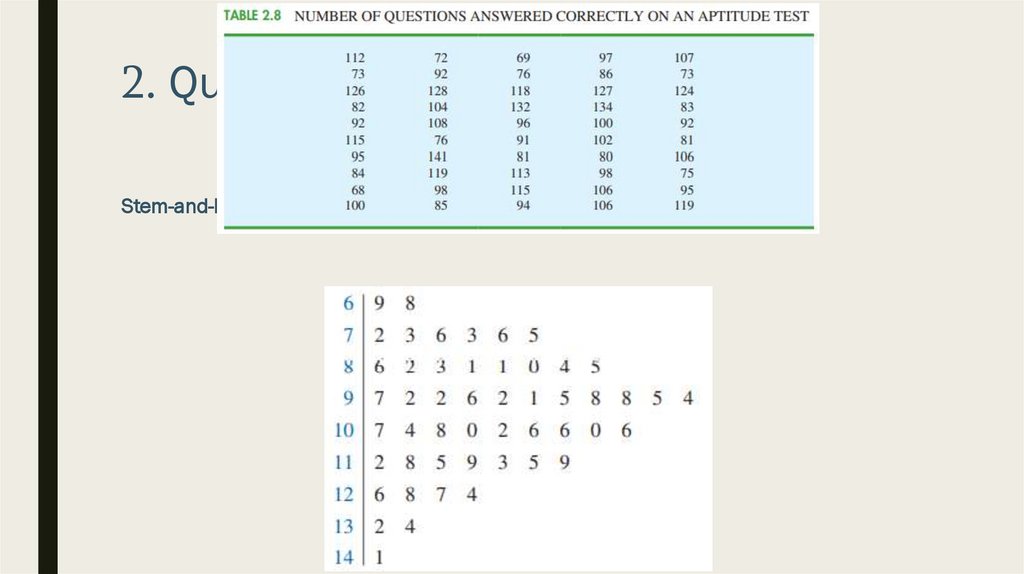
2. Quantitative Variable
Stem-and-Leaf Display
■ Graphical display used to show simultaneously the rank order and shape of a
distribution of data
■ Let’s use following example for demonstration

38.

2. Quantitative Variable
Stem-and-Leaf Display

39.

2. Quantitative Variable
Stem-and-Leaf Display

40.

2. Quantitative Variable
Stem-and-Leaf Display

41.

2. Quantitative Variable
Stem-and-Leaf Display
■ In the end we have the rank order and form of the distribution

42.

3. Descriptive Statistics for Two Variable
■ Thus far we have focused on using tabular and graphical displays to summarize the
data for a single categorical or quantitative variable
■ In most cases, we have data for two or more variables
■ In this section we will concentrate on summarizing data for two variables using
tables

43.

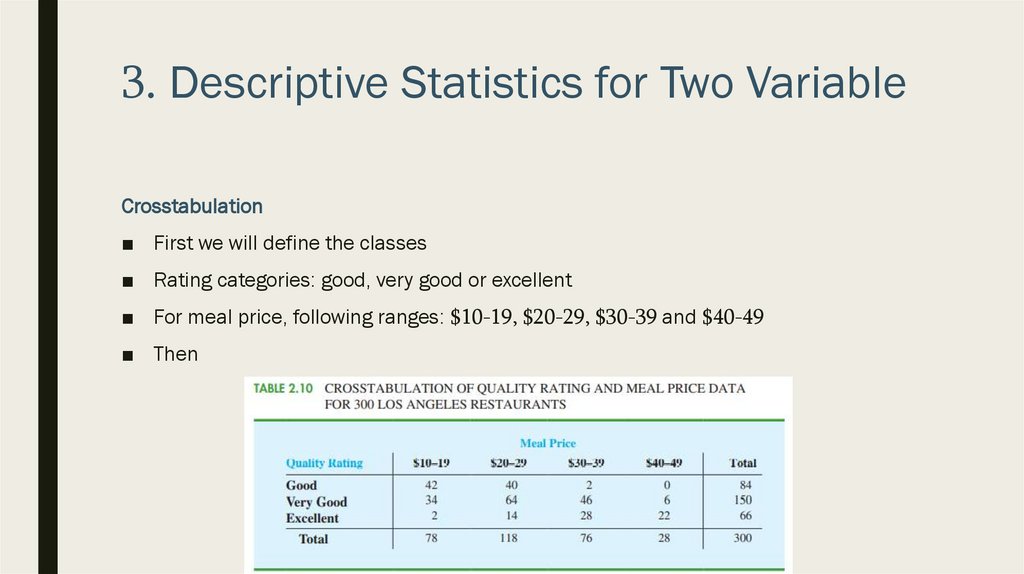
3. Descriptive Statistics for Two Variable
Crosstabulation
■ Is a tabular summary of data for
two variables
■ Let’s use following data for
demonstration

44.

3. Descriptive Statistics for Two Variable
Crosstabulation
■ First we will define the classes
■ Rating categories: good, very good or excellent
■ For meal price, following ranges: $10-19, $20-29, $30-39 and $40-49
■ Then

45.

3. Descriptive Statistics for Two Variable
Crosstabulation
■ What can be learned from crosstabulation:
– Larges restaurants with the rating of “very good” fell in the price class of $20-2
– Only 2 restaurants fell in rating “excellent” from $10-19 price range
– etc

46.

3. Descriptive Statistics for Two Variable
Crosstabulation
■ Right and bottom margins provide frequency distribution for each variable
■ What can be learned
– There are 84 restaurants in “good” class
– Or 78 restaurants in $10-19 class
– etc

47.

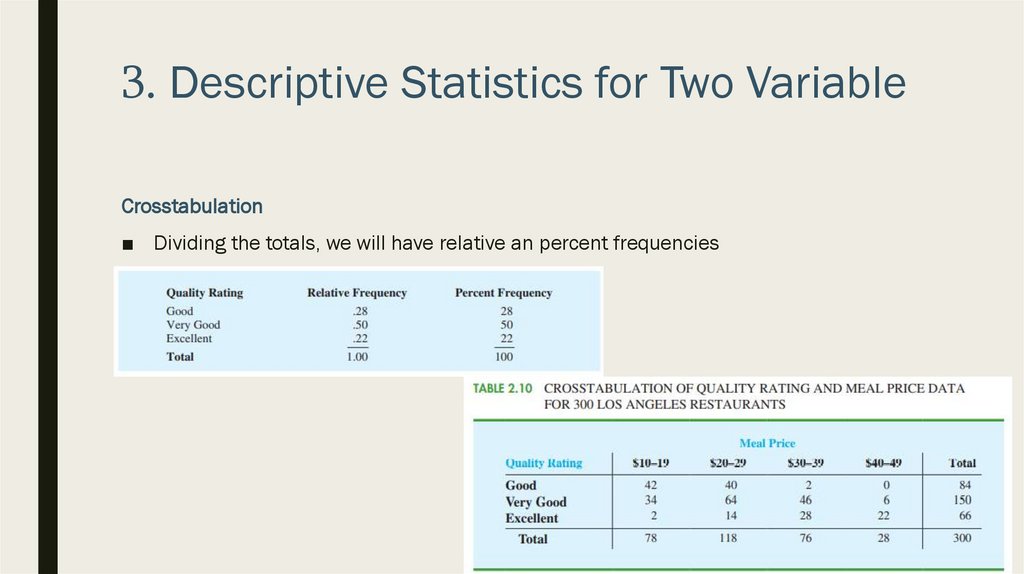
3. Descriptive Statistics for Two Variable
Crosstabulation
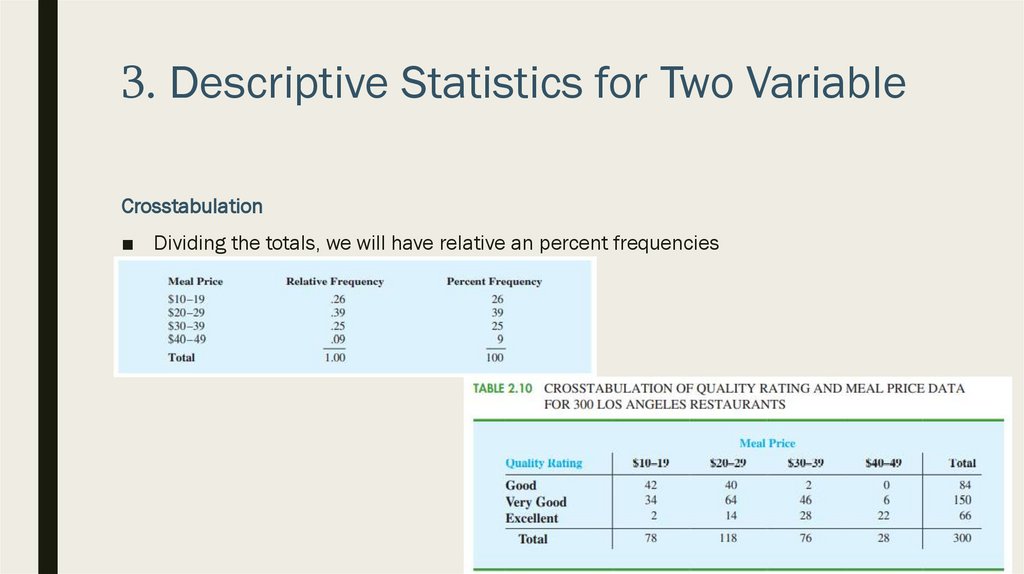
■ Dividing the totals, we will have relative an percent frequencies

48.

3. Descriptive Statistics for Two Variable
Crosstabulation
■ Dividing the totals, we will have relative an percent frequencies

49.

3. Descriptive Statistics for Two Variable
Crosstabulation
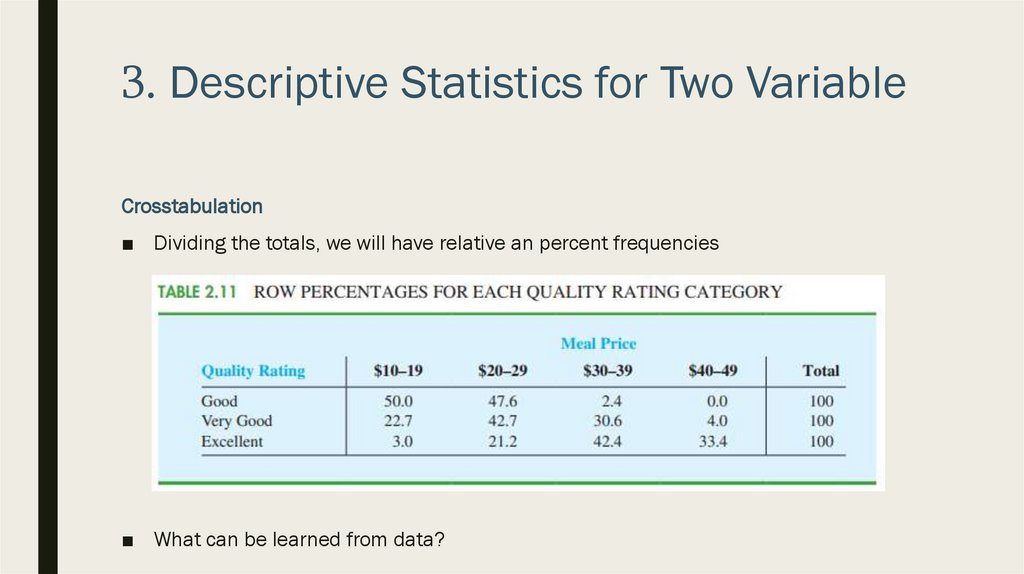
■ Dividing the totals, we will have relative an percent frequencies
■ What can be learned from data?

50.

3. Descriptive Statistics for Two Variable
Crosstabulation
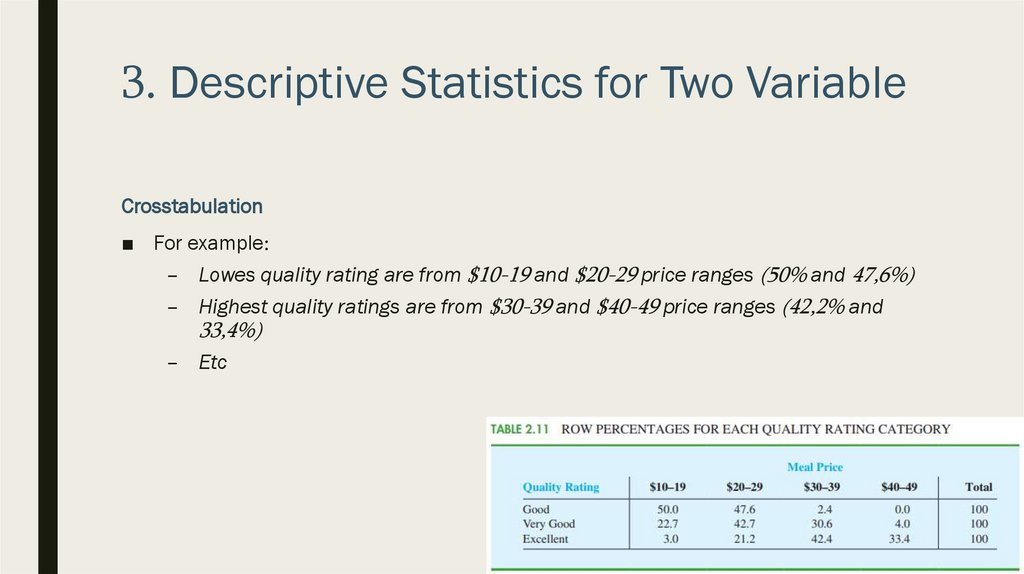
■ For example:
– Lowes quality rating are from $10-19 and $20-29 price ranges (50% and 47,6%)
– Highest quality ratings are from $30-39 and $40-49 price ranges (42,2% and
33,4%)
– Etc

51.

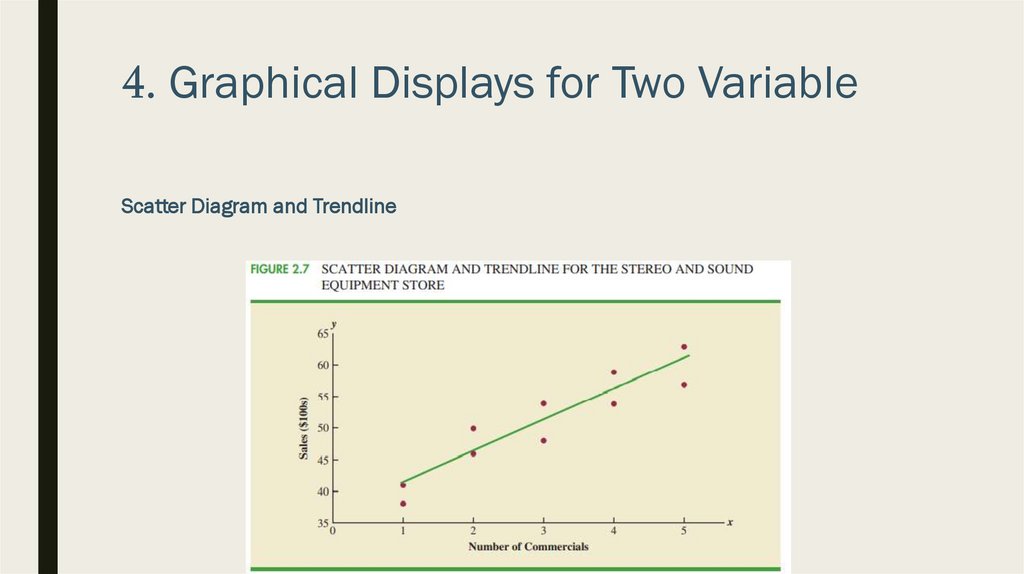
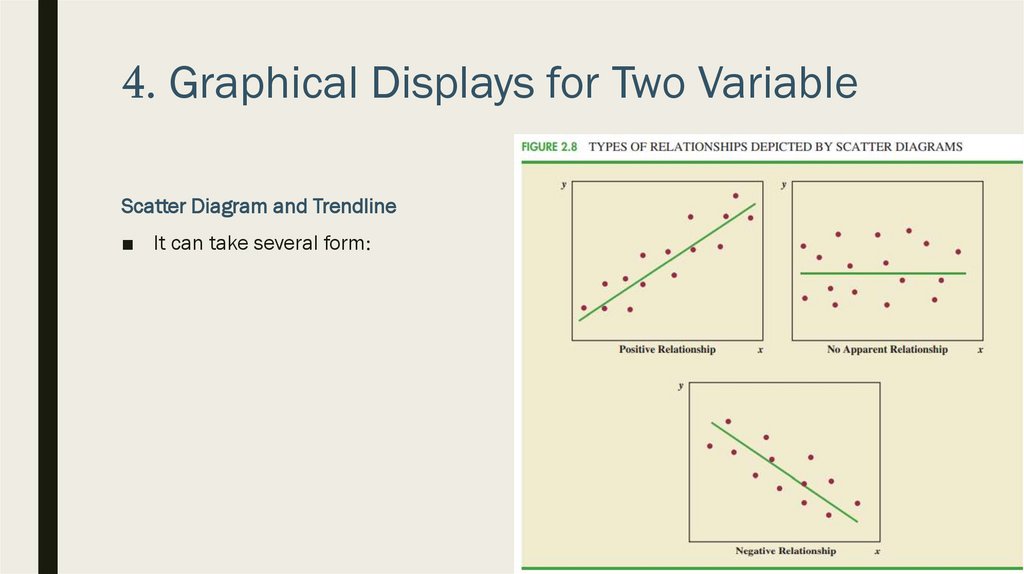
4. Graphical Displays for Two Variable
Scatter Diagram and Trendline
■ Scatter diagram is a graphical display of the relationship between two quantitative
variables
■ Trendline is a line that provides an approximation of the relationship

52.

4. Graphical Displays for Two Variable
Scatter Diagram and Trendline
■ Let’s consider following example
■ Is there a relationship between variables? What if we have 1000 data points?

53.

4. Graphical Displays for Two Variable
Scatter Diagram and Trendline

54.

4. Graphical Displays for Two Variable
Scatter Diagram and Trendline
■ It can take several form:

55.

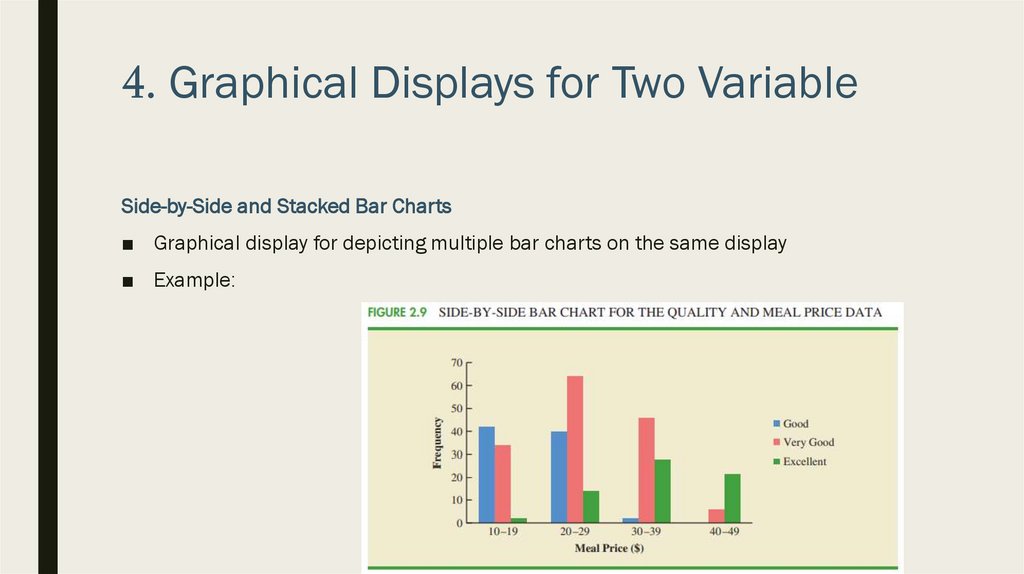
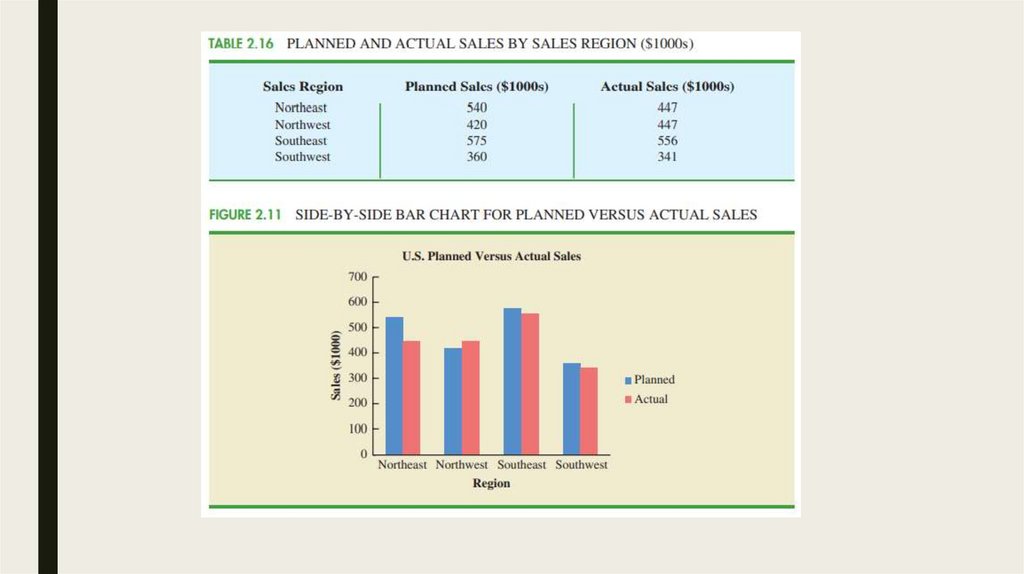
4. Graphical Displays for Two Variable
Side-by-Side and Stacked Bar Charts
■ Graphical display for depicting multiple bar charts on the same display
■ Example:

56.

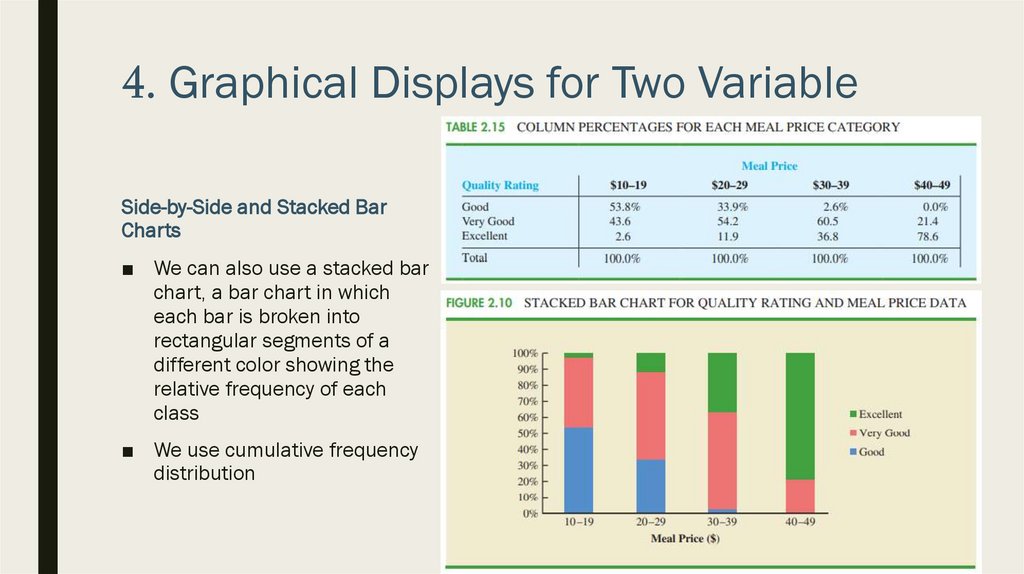
4. Graphical Displays for Two Variable
Side-by-Side and Stacked Bar
Charts
■ We can also use a stacked bar
chart, a bar chart in which
each bar is broken into
rectangular segments of a
different color showing the
relative frequency of each
class
■ We use cumulative frequency
distribution

57.

Practical Examples

58.

59.

60.

61.

62.

Thank you!