Статистика-Презентация-05 Средние вел.допол

1. Тема Средние величины

2. Вопросы темы:

1. Сущность и виды средних в статистике
2. Средняя арифметическая
3. Средняя гармоническая
4. Средняя геометрическая
5. Структурные показатели: мода и медиана
6. Основные правила применения средних в
статистике

3. 1. Сущность и виды средних в статистике

В средней выражается то общее и типичное, что
характерно для совокупности в отношении
изучаемого признака.
Она в одной величине показывает общую меру
этого признака, имеющего различное значение у
единиц совокупности.

4. 1. Сущность и виды средних в статистике

Средней
величиной
в
статистике
называется обобщенная характеристика
совокупности однотипных явлений по
какому-либо
количественно
варьирующему признаку.
Средняя величина показывает уровень
этого признака, отнесенный к единице
совокупности.

5. 1. Сущность и виды средних в статистике

Важно, чтобы средние величины были
основаны на массовом обобщении
фактов.
Закон больших чисел создает условия,
чтобы в средней проявился типичный
уровень варьирующего признака в
конкретных условиях места и времени.

6. 1. Сущность и виды средних в статистике

Средние, применяемые в статистике, относятся
к классу степенных средних, общая формула
которых имеет следующий вид:
x
m
xm
n
где `x – степенная средняя;
x – меняющиеся величины признака (варианты);
n – число вариант;
m – показатель степени средней;
S - знак суммирования.

7. 1. Сущность и виды средних в статистике

При различных значениях показателя
степени средней (m) получаются
различные виды средней величины:
m = 1 - средняя арифметическая;
m = 2 - средняя квадратическая;
m = 3 - средняя кубическая;
m = -1 - средняя гармоническая;
m = 0 - средняя геометрическая.

8. 1. Сущность и виды средних в статистике

Чем больше показатель степени, тем
больше
величина
средней
(правило
мажорантности средних).
Средняя только тогда будет верной
обобщающей характеристикой совокупности по варьирующему признаку, когда
при замене всех вариант средней общий
объем варьирующего признака остается
неизменным.

9. 1. Сущность и виды средних в статистике

Формулы различных видов степенных средних величин

10. 1. Сущность и виды средних в статистике

Средняя квадратическая применяется в тех
случаях, когда исходные значения X могут
быть как положительными, так и отрицательными, например при расчете средних
отклонений.
Главной сферой применения квадратической
средней
является
измерение
вариации значений X, о чем пойдет речь в
след. теме.

11. 1. Сущность и виды средних в статистике

Средняя
кубическая
применяется
крайне редко, например, при расчете
индексов
нищеты
населения
для
развивающихся стран (ИНН-1) и для
развитых
(ИНН-2),
предложенных
и
рассчитываемых ООН.

12. 1. Сущность и виды средних в статистике

2. Средняя арифметическая
Средняя арифметическая есть частное
от деления суммы вариант на их число.
Чтобы
исчислить
среднюю
арифметическую, нужно сложить все отдельные
варианты и сумму разделить на их число:
`x = (Sx) / n.
Приведенная
выше
формула
есть
формула
средней
арифметической
простой (невзвешенной).

13. 1. Сущность и виды средних в статистике

2. Средняя арифметическая
Например, студент сдал 4 экзамена и
получил следующие оценки: 3, 4, 4 и 5.
Рассчитаем средний балл по формуле
средней арифметической простой:
?????

14. 1. Сущность и виды средних в статистике

2. Средняя арифметическая
Например, студент сдал 4 экзамена и
получил следующие оценки: 3, 4, 4 и 5.
Рассчитаем средний балл по формуле
средней арифметической простой:
(3+4+4+5)/4 = 16/4 = 4.

15. 1. Сущность и виды средних в статистике

2. Средняя арифметическая
Если
варианты
имеют
одинаковые
значения, то среднюю арифметическую
можно исчислить путем перемножения
различных значений вариант на их частоту
(вес), а затем сумму произведений вариант
разделить на сумму частот (весов):
`x = S(xi *fi) /Sfi.

16. 1. Сущность и виды средних в статистике

2. Средняя арифметическая
Наиболее часто встречаются следующие
приемы вычисления средней арифметической:
1.
Если
имеются
все
значения
варьирующего признака, полученные в
результате наблюдения, то используют
формулу
средней
арифметической
простой. Если же данные представлены в
виде различных значений вариант и их
частот, то применяют формулу средней
арифметической взвешенной.

17. 2. Средняя арифметическая

2. Если имеется готовая сумма варьирующих признаков и соответствующая ей
численность совокупности, то среднюю
арифметическую определяют путем их
деления.
3. Среднюю арифметическую вычисляют
на основе вариационного ряда.

18. 2. Средняя арифметическая

Если ряд дискретен, то расчет средней
арифметической
производится
по
формуле
средней
арифметической
взвешенной.
Если же ряд интервальный, то его нужно
привести, прежде всего, к дискретному
виду.
Для
этого
обычно
интервал
заменяют
его
средним
значением,
определяемым как полусумма верхней и
нижней границ.

19. 2. Средняя арифметическая

Определите
среднее число
детей в семье.
Какую формулу
средней можем
использовать?
Число детей
Число
в семье
семей
(варианты x) (частота f)
0
10
1
30
2
75
3
45
4
20
5
15
6
5
Итого
200
Число
детей
(xf)

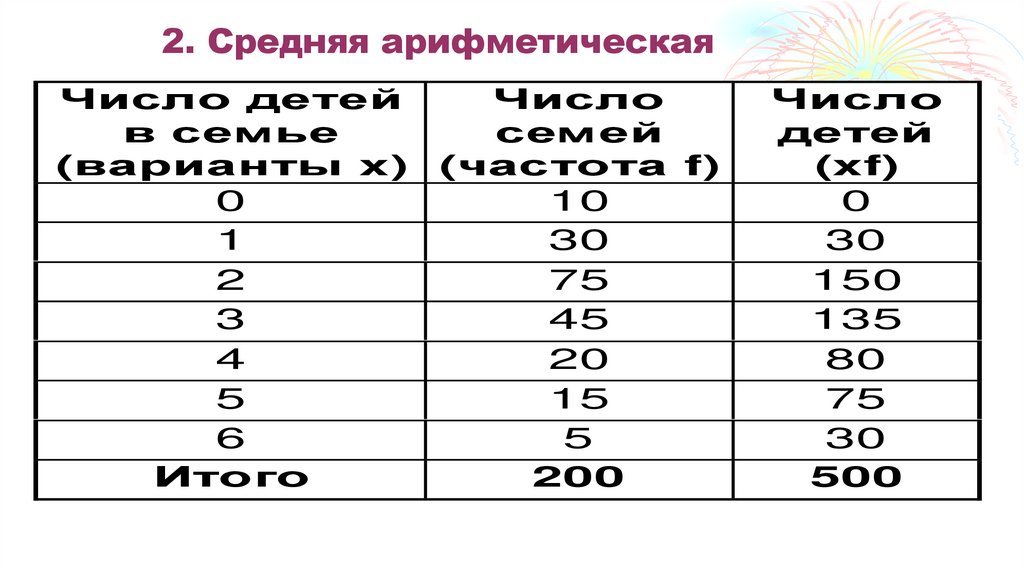
20. 2. Средняя арифметическая

Число детей
в семье
(варианты x)
0
1
2
3
4
5
6
Итого
Число
семей
(частота f)
10
30
75
45
20
15
5
200
Число
детей
(xf)
0
30
150
135
80
75
30
500

21. 2. Средняя арифметическая

Если ряд дискретен, то расчет средней
арифметической произво-дится по формуле
средней арифметической взвешенной.
x = (Sxifi) /Sfi.
X = 500/200 =2,5

22. 2. Средняя арифметическая

Необходимо найти
среднюю заработную
плату рабочих.
Какую формулу
средней можем
использовать?

23. 2. Средняя арифметическая

Группа
рабочих по
заработной
плате, у.е.
13000-14000
Серединное
значение
интервала
(x)
Число
рабоч
их (f)
10
14000-15000
50
15000-16000
100
16000-17000
115
17000-18000
180
18000-19000
45
Итого
500
Произведен
ие вариант
на частоты
(xf)

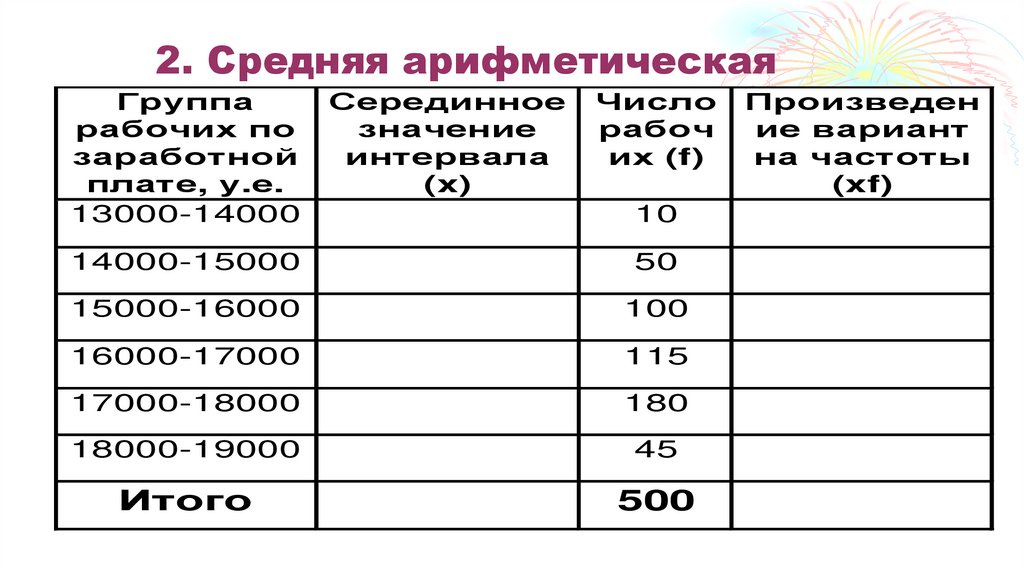
24. 2. Средняя арифметическая

Группа
рабочих по
заработной
плате, у.е.
13000-14000
Серединное
значение
интервала
(x)
13500
Число
рабоч
их (f)
10
Произведен
ие вариант
на частоты
(xf)
135 000
14000-15000
14500
50
725 000
15000-16000
15500
100
1 550 000
16000-17000
16500
115
1 897 500
17000-18000
17500
180
3 150 000
18000-19000
18500
45
832 500
500
8 290 000
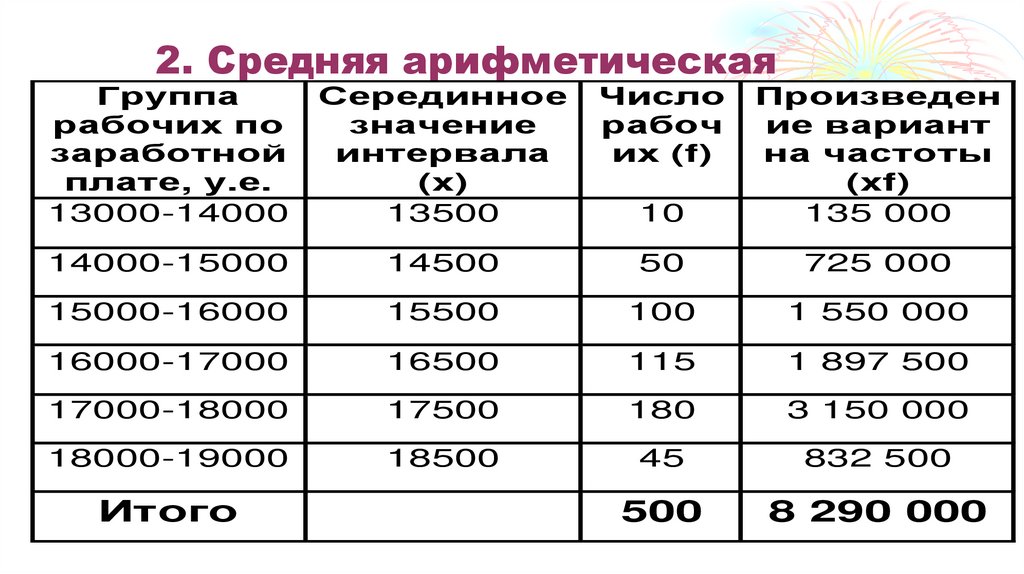
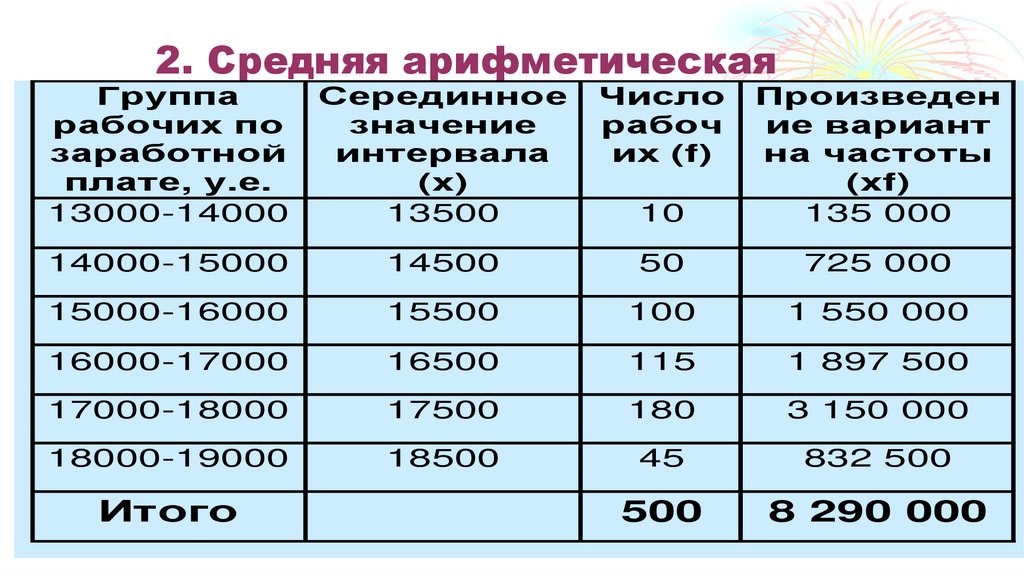
Итого

25. 2. Средняя арифметическая

Если же ряд интервальный, то его нужно
привести, прежде всего, к дискретному
виду.
Для
этого
обычно
интервал
заменяют
его
средним
значением,
определяемым как полусумма верхней и
нижней границ.
_
x = (Sxifi) /Sfi.
_
х = 8 290 000/500 = 16580 тенге

26. 2. Средняя арифметическая

Средняя арифметическая обладает рядом
важнейших
свойств,
имеющих
практическое значение для вычисления
средней по данным вариационного ряда.
1. Произведение средней на сумму частот
всегда равно сумме произведений вариант
на частоты:
` x * Sfi = S(xi * fi )
В нашем случае ?

27. 2. Средняя арифметическая

Средняя арифметическая обладает рядом
важнейших
свойств,
имеющих
практическое значение для вычисления
средней по данным вариационного ряда.
1. Произведение средней на сумму частот
всегда равно сумме произведений вариант
на частоты:
`x * Sfi = S(xi * fi )
В нашем случае 16 580*500 = 8 290 000.

28. 2. Средняя арифметическая

2. Если от каждой варианты отнять какоелибо произвольное число, то новая средняя
уменьшится на то же число:
[S(xi - A)*fi] / Sfi = `x – A.
Отсюда
`x = [S (xi - A)*fi] / Sfi + A.

29. 2. Средняя арифметическая

3.Если к каждой варианте
прибавить
какое-либо
произвольное
число,
то
средняя увеличится на это же число:
[S(xi+ A)*fi]/Sfi = `x + A.
Отсюда
_
x = [S(xi + A)* fi] / Sfi - A.
Свойство 3 аналогично свойству 2.

30. 2. Средняя арифметическая

4. Если каждую варианту разделить на
какое-либо
произвольное
число,
то
средняя арифметическая уменьшится во
столько же раз:
[S(xi / A) * fi] / Sfi=`x / A.
Отсюда
`x = {[S(xi/ A)* fi] / Sfi} × A,

31. 2. Средняя арифметическая

5. Если каждую варианту умножить на
какое-либо произвольное число, то средняя
арифметическая увеличится во столько же
раз:
[S(xi × A) *fi] /Sfi = `x × A.
Отсюда
`x = {[Sxi × A) *fi] / Sfi} / A.
Свойство 5 аналогично свойству 4.

32. 2. Средняя арифметическая

6. Если все частоты (веса) разделить или
умножить на какое-либо число, то
средняя арифметическая от этого не
изменится.
Этим
свойством
часто
пользуются,
выражая веса (частоты) в процентах к
итогу.

33. 2. Средняя арифметическая

Пользуясь
разными
свойствами
средней
арифметической,
можно
вычислить
ее
следующим способом:
1) путем вычитания из всех вариант постоянного
числа (лучшее значение серединной варианты
или варианты с наибольшей частотой, в данном
примере ?);
2) путем деления варианты на постоянное число.
а именно на величину интервала (в нашем
примере ?);
3) путем выражения частот в процентах.
Первые два способа называются способом
отсчета от условного начала, или сокращенно
“способом моментов”. Он применяется в рядах с
равными интервалами.

34. 2. Средняя арифметическая

Группа
рабочих по
заработной
плате, у.е.
13000-14000
Серединное
значение
интервала
(x)
13500
Число
рабоч
их (f)
10
Произведен
ие вариант
на частоты
(xf)
135 000
14000-15000
14500
50
725 000
15000-16000
15500
100
1 550 000
16000-17000
16500
115
1 897 500
17000-18000
17500
180
3 150 000
18000-19000
18500
45
832 500
500
8 290 000
Итого

35. 2. Средняя арифметическая

Пользуясь
разными
свойствами
средней
арифметической,
можно
вычислить
ее
следующим способом:
1) путем вычитания из всех вариант постоянного
числа (лучшее значение серединной варианты
или варианты с наибольшей частотой, в данном
примере 16 500);
2) путем деления варианты на постоянное число.
а именно на величину интервала (в нашем
примере 1000);
3) путем выражения частот в процентах.
Первые два способа называются способом
отсчета от условного начала, или сокращенно
“способом моментов”. Он применяется в рядах с
равными интервалами.

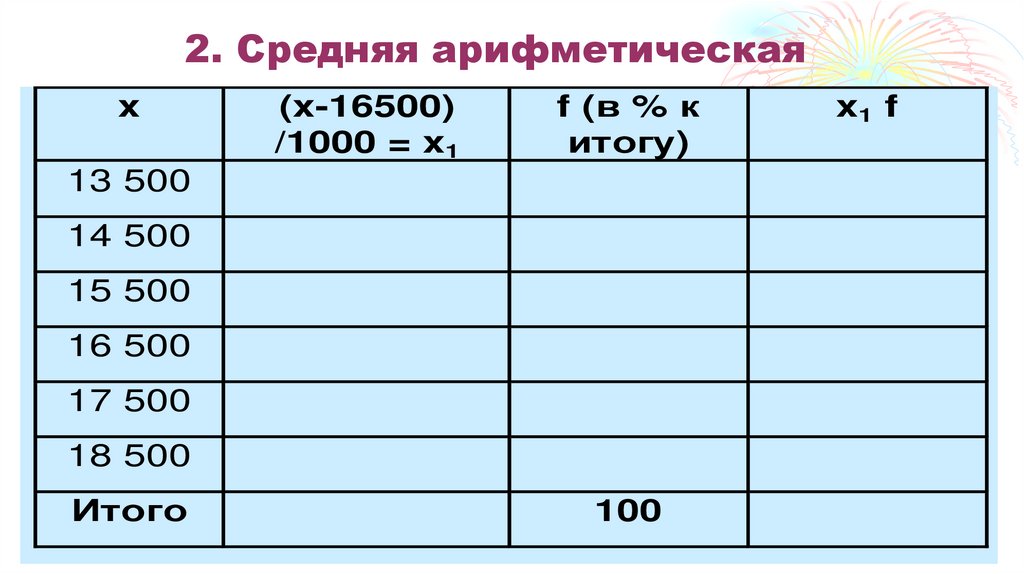
36. 2. Средняя арифметическая

x
(x-16500)
/1000 = x1
f (в % к
итогу)
13 500
14 500
15 500
16 500
17 500
18 500
Итого
100
x1 f

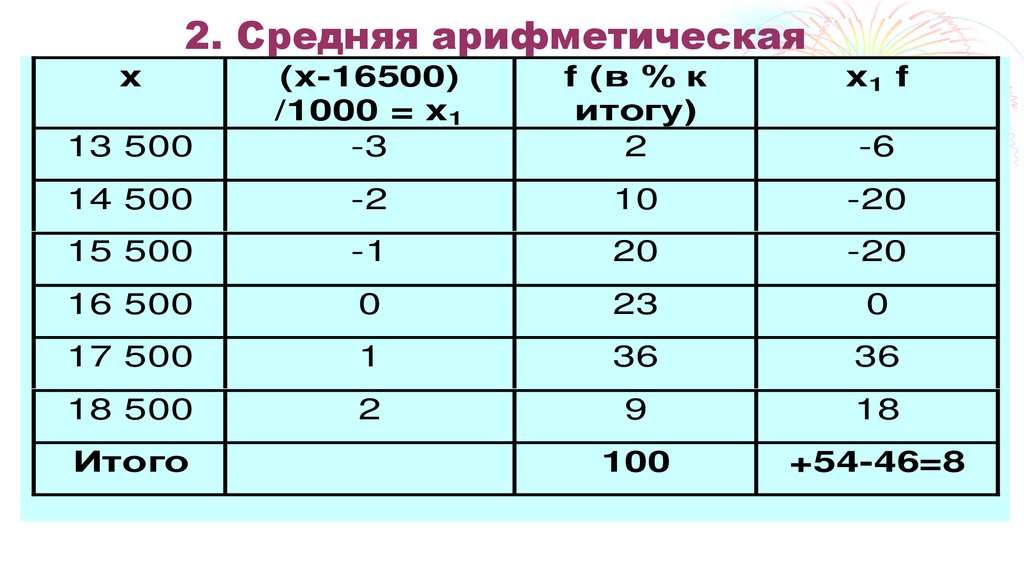
37. 2. Средняя арифметическая

f (в % к
итогу)
2
x1 f
13 500
(x-16500)
/1000 = x1
-3
14 500
-2
10
-20
15 500
-1
20
-20
16 500
0
23
0
17 500
1
36
36
18 500
2
9
18
100
+54-46=8
x
Итого
-6

38. 2. Средняя арифметическая

Среднюю арифметическую из этих новых
вариант (m1) называют моментом первого
порядка и выражают формулой:
m1= (S x1f) / Sf = ?

39. 2. Средняя арифметическая

Среднюю арифметическую из этих новых
вариант (m1) называют моментом первого
порядка и выражают формулой:
m1= (S x1f) / Sf =8/100 = 0,08.

40. 2. Средняя арифметическая

Чтобы определить величину средней
арифметической,
нужно
величину
момента первого порядка умножить на
величину интервала (i), на который делили
все варианты (в нашем случае на 1000) и
прибавить к полученному произведению
величину варианты (то есть A), которую
вычитали:
_
x = i * m1 + A = ?

41. 2. Средняя арифметическая

Чтобы определить величину средней
арифметической,
нужно
величину
момента первого порядка умножить на
величину интервала, на который делили
все варианты (в нашем случае на 1000) и
прибавить к полученному произведению
величину варианты, которую вычитали:
_
x = i m1 + A = 1000*0,08 + 16 500 =16 580.

42. 2. Средняя арифметическая

3. Средняя гармоническая
Сред.гармоническая: когда статистическая информация не
содержит частот f по отдельным вариантам х совокупности,
а представлена как их произведение: х*f, то тогда
применяется формула средней гармонической взвешенной, чтобы исчислить среднюю, обозначим х*f=w откуда
определим f=w/х получим формулу:
В тех случаях, когда вес каждого варианта равен единице
(индивидуальные
значения
обратного
признака
встречаются по одному разу), применяется формула средней гармоническая простая.

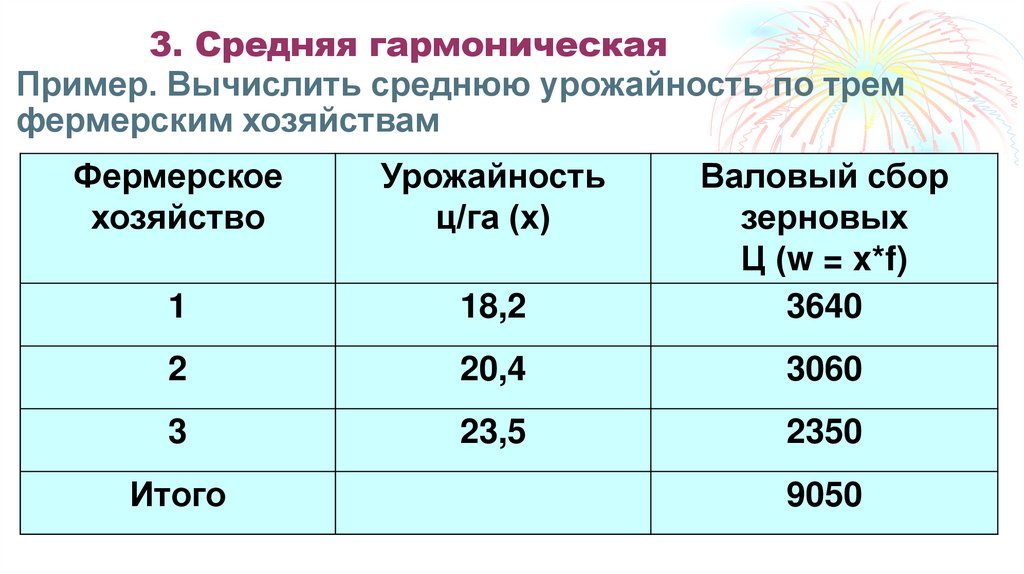
43. 2. Средняя арифметическая

3. Средняя гармоническая
Пример. Вычислить среднюю урожайность по трем
фермерским хозяйствам
Фермерское
хозяйство
Урожайность
ц/га (х)
1
18,2
Валовый сбор
зерновых
Ц (w = x*f)
3640
2
20,4
3060
3
23,5
2350
Итого
9050

44. 2. Средняя арифметическая

3. Средняя гармоническая
Средняя
гармоническая
есть
по
существу
преобразованная
средняя
арифметическая, которая применяется
тогда, когда неизвестна численность
совокупности и приходится взвешивать
варианты по объемам признака.

45. 2. Средняя арифметическая

3. Средняя гармоническая
В тех случаях, когда произведение х*f
одинаково или равно 1 (m=1) для расчета
применяют
среднюю
гармоническую
простую, вычисляемую по формуле:
Средняя гармоническая простая — показатель, обратный средней арифметической
простой,
исчисляемый
из
обратных
значений признака.

46. 2. Средняя арифметическая

3. Средняя гармоническая

47. 3. Средняя гармоническая

4. Средняя геометрическая
Средняя геометрическая (простая) используется
при
вычислении
среднего
коэффициента роста (темпа)
в рядах
динамики, если промежутки времени, к
которым относятся коэффициенты роста,
одинаковы.
Если средние коэффициенты роста относятся
к
периодам
различной
продолжительности, то общий средний коэффициент
роста за весь период определяется по
формуле средней геометрической взвешенной
(fi - продолжительность периода, к которому
относится средний коэффициент роста).

48. 3. Средняя гармоническая

4. Средняя геометрическая

49. 3. Средняя гармоническая

4. Средняя геометрическая

50. 3. Средняя гармоническая

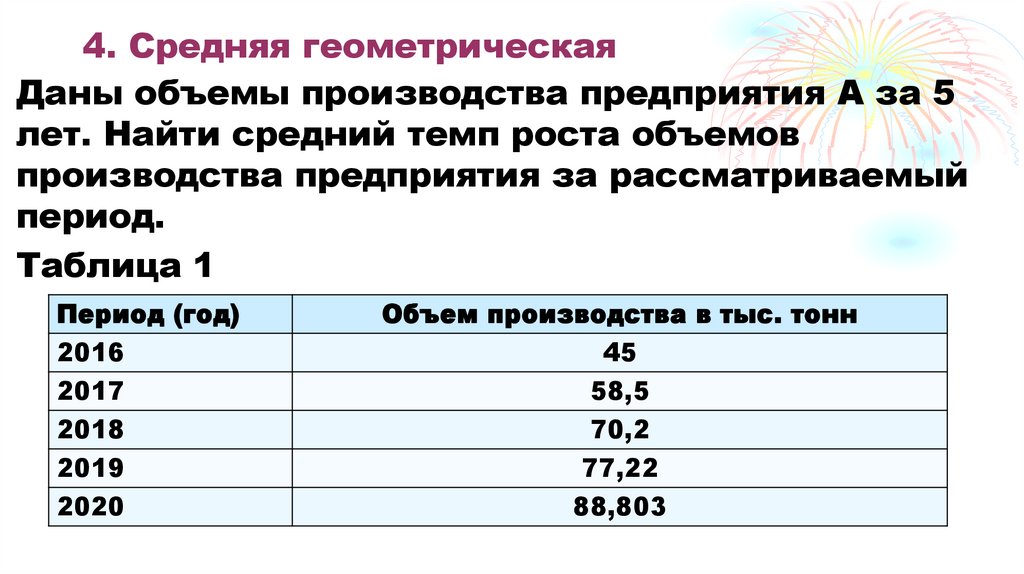
4. Средняя геометрическая

51. 3. Средняя гармоническая

4. Средняя геометрическая
Даны объемы производства предприятия А за 5
лет. Найти средний темп роста объемов
производства предприятия за рассматриваемый
период.
Таблица 1
Период (год)
2016
Объем производства в тыс. тонн
45
2017
2018
58,5
70,2
2019
2020
77,22
88,803

52. 3. Средняя гармоническая

4. Средняя геометрическая
Даны объемы производства предприятия А за 5
лет. Найти средний темп роста объемов
производства предприятия за рассматриваемый
период.

53. 4. Средняя геометрическая

Даны объемы производства предприятия А за
5 лет. Найти средний темп роста объемов
производства
предприятия
за
рассматриваемый период.

54. 4. Средняя геометрическая

Для
определения
средней
взвешенной применяется формула:
геометрической

55. 4. Средняя геометрическая

Среднемесячные темпы роста производства продукции:
январь-март-106,2%;
апрель-август–108,5%.
Среднемесячный темп роста производства продукции
за период январь-август:

56. 4. Средняя геометрическая

Среднемесячный темп роста производства продукции
за период январь-август:

57. 4. Средняя геометрическая

5. Мода и медиана
Мода и медиана являются вспомогательными
описательными
характеристиками
центра
распределения варьирующего признака.
Модой
называется
величина
признака
(варианта), которая чаще всего встречается в
данной совокупности. В вариационном ряду это
будет варианта, имеющая наибольшую частоту.
Медианой называется варианта, которая
находится в середине вариационного ряда.
Медиана делит ряд пополам, по обе стороны от
нее находится одинаковое количество единиц
совокупности.

58. 4. Средняя геометрическая

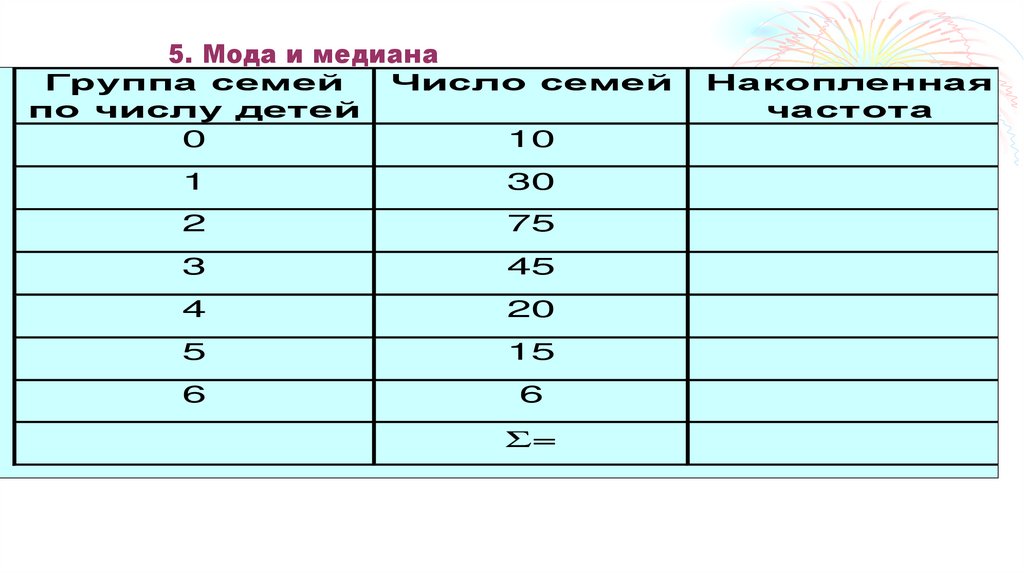
5. Мода и медиана

59. 4. Средняя геометрическая

5. Мода и медиана
Медиана соответствует варианту, стоящему в
середине ранжированного ряда. Положение
медианы определяется ее номером:
NMe = n+1 / 2
NMe - номер медианы
Примечание - При нечетном количестве
единиц совокупности
прибавляют 1.
к сумме всех частот

60. 4. Средняя геометрическая

5. Мода и медиана
Группа семей
по числу детей
0
Число семей
1
30
2
75
3
45
4
20
5
15
6
6
10
S=
Накопленная
частота

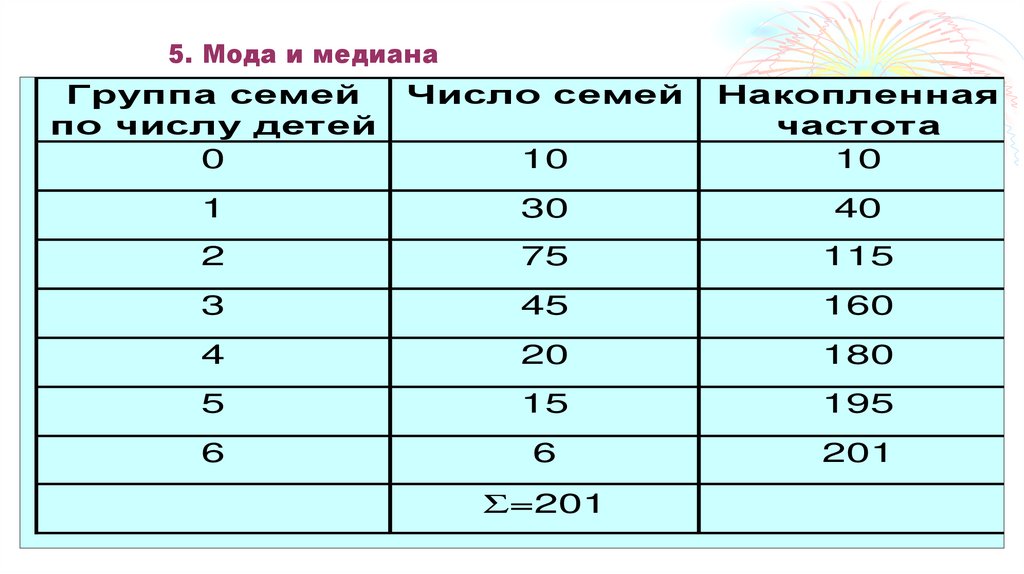
61. 4. Средняя геометрическая

5. Мода и медиана
Группа семей
по числу детей
0
Число семей
10
Накопленная
частота
10
1
30
40
2
75
115
3
45
160
4
20
180
5
15
195
6
6
201
S=201

62. 4. Средняя геометрическая

5. Мода и медиана
Модой в этом примере будет семья,
имеющая двоих детей, так как этому
значению
варианты
соответствует
наибольшее число семей (75).
Вариационный ряд имеющий одну моду
называется унимодальным.

63. 5. Мода и медиана

Если распределение равномерное, где
все варианты встречаются одинаково часто,
то говорят, что ряд не имеет моды или,
иначе,
что
все
варианты
одинаково
модальны.
Могут быть случаи, когда две варианты
встречаются одинаково часто. Тогда
говорят, что распределение бимодально,
три и более – мультимодальным.

64. 5. Мода и медиана

Если ряд распределения дискретный, то
медиана
находится
как
серединное
значение признака (например, если число
значений нечетное – 45, то соответствует
23 значению признака в ряду значений,
расположенных в порядке возрастания,
Если число значений четное – 44, то
медиана
соответствует
22
значению
признака).

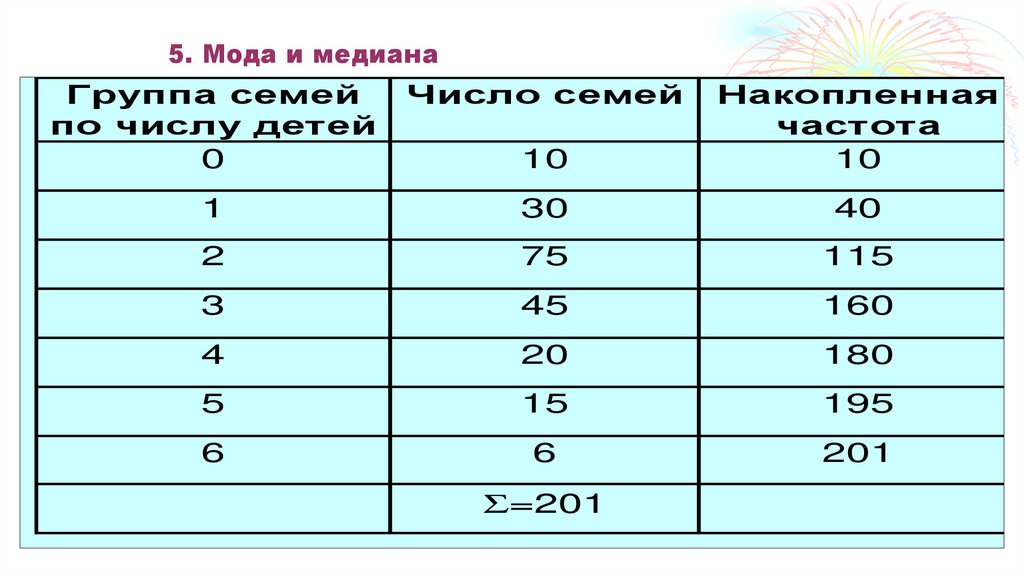
65. 5. Мода и медиана

Группа семей
по числу детей
0
Число семей
10
Накопленная
частота
10
1
30
40
2
75
115
3
45
160
4
20
180
5
15
195
6
6
201
S=201

66. 5. Мода и медиана

В нашем примере это будет ________
101-я варианта ((201+1)/2 ).
Данная варианта находится в группе семей
с двумя детьми, то есть медианой будет
семья, имеющая двух детей. Вывод: 50%
семей имеют двух детей и менее.

67. 5. Мода и медиана

Группа рабочих по
зарплате,тенге
260 000-280 000
280 000-300 000
300 000-320 000
320 000-340 000
340 000-360 000
360 000-380 000
ИТОГО
Число рабочих
10
50
100
115
180
45
500
Кумулятивная
частота

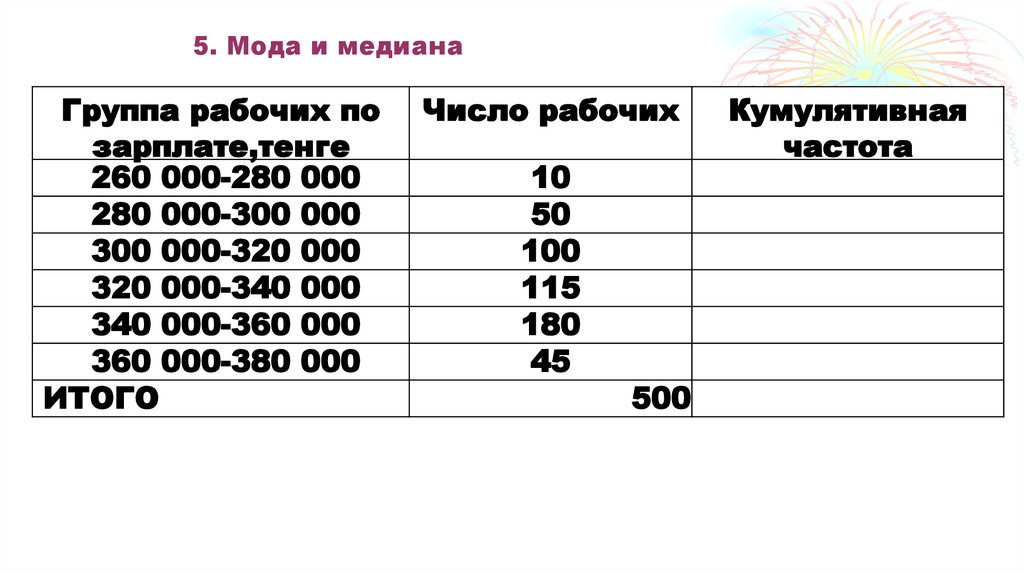
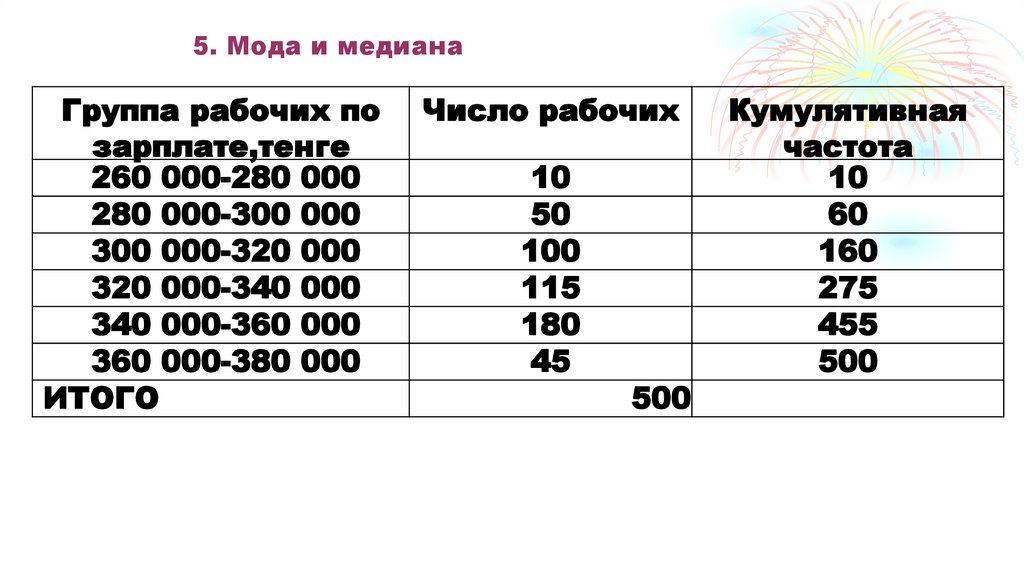
68. 5. Мода и медиана

Группа рабочих по
зарплате,тенге
260 000-280 000
280 000-300 000
300 000-320 000
320 000-340 000
340 000-360 000
360 000-380 000
ИТОГО
Число рабочих
10
50
100
115
180
45
500
Кумулятивная
частота
10
60
160
275
455
500
Модальным интервалом будет???

69. 5. Мода и медиана

Модальным интервалом здесь является
интервал, где варианта лежит в пределах
от __ до __ тыс. тенге.

70. 5. Мода и медиана

Модальным интервалом здесь
является интервал, где варианта лежит
в пределах от 340 до 360 тыс. тенге,
поскольку наибольшее количество
рабочих имеют заработную плату
именно в этих пределах.

71. 5. Мода и медиана

Для расчета определенного значения модальной
величины признака, заключенного в этом
интервале, применяют такую формулу:
где xMo – минимальная граница модального интервала (в
примере – ?),
i – величина модального интервала (у нас – ?),
fMo-1 – частота интервала, предшествующего модальному
(в нашем примере – ?),
fMo – частота модального интервала (?),
fMo+1 -частота интервала, следующего за модальным (?).

72. 5. Мода и медиана

Группа рабочих по
зарплате,тенге
260 000-280 000
280 000-300 000
300 000-320 000
320 000-340 000
340 000-360 000
360 000-380 000
ИТОГО
Число рабочих
10
50
100
115
180
45
500
Кумулятивная
частота
10
60
160
275
455
500

73. 5. Мода и медиана

Для расчета определенного значения модальной
величины признака, заключенного в этом
интервале, применяют такую формулу:
где xMo – минимальная граница модального интервала (в
примере – 340 000),
i – величина модального интервала (у нас – 20 000),
fMo-1 – частота интервала, предшествующего модальному
(в нашем примере – 115),
fMo – частота модального интервала (180),
fMo+1 -частота интервала, следующего за модальным (45).

74. 5. Мода и медиана

Рассчитаем значение моды для нашего
примера:
Mo = 340 000 + (20 000 * (180 – 115) / [(180 –
115) +(180 – 45)] = 340 000 +(20 000*65/200)
= 340 000 + (20 000 * 0,325 )= 346 500 тенге
Модальный
размер
зарплаты
составляет 346 500 тенге, то есть этот
размер
зарплаты
наиболее
часто
встречаемый размер.

75. 5. Мода и медиана

Если
ряд
интервальный,
то
первоначально
находят
медианный
интервал,
находящегося
в
середине
ранжированного ряда.
Таким
интервалом
будет
такой,
кумулятивная частота которого будет
превышать половину суммы частот.

76. 5. Мода и медиана

Группа рабочих по
зарплате,тенге
260 000-280 000
280 000-300 000
300 000-320 000
320 000-340 000
340 000-360 000
360 000-380 000
ИТОГО
Число рабочих
10
50
100
115
180
45
500
Кумулятивная
частота
10
60
160
275
455
500

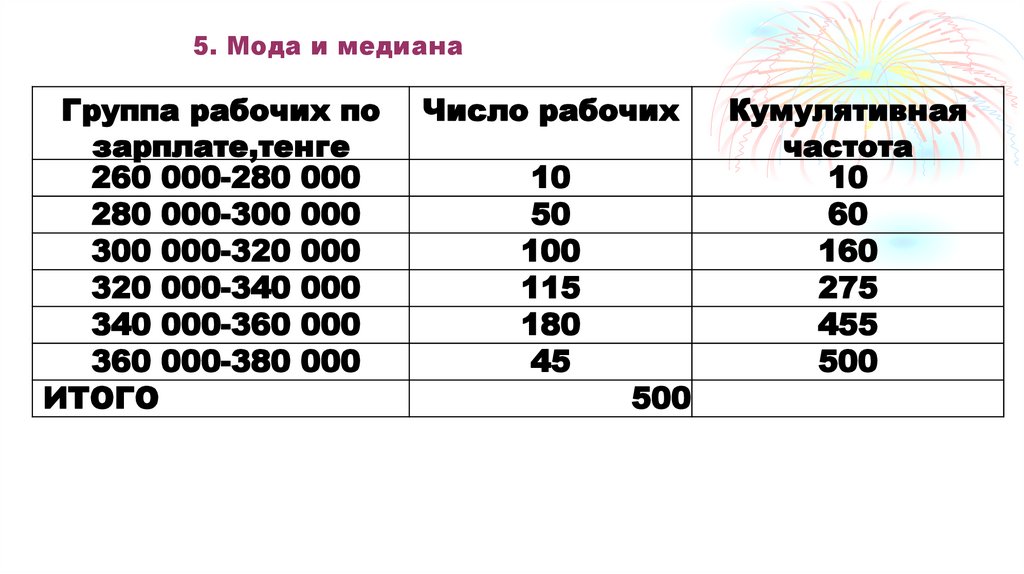
77. 5. Мода и медиана

Половина частот у нас равна 250 (500/2).
Суммируя последовательно частоты в
ряду, мы превысим середину суммы частот
на четвертом интервале (10 + 50 + 100 + 115
= 275), то есть
Медианным у нас будет интервал 320 000340 000 тенге.

78. 5. Мода и медиана

79. 5. Мода и медиана

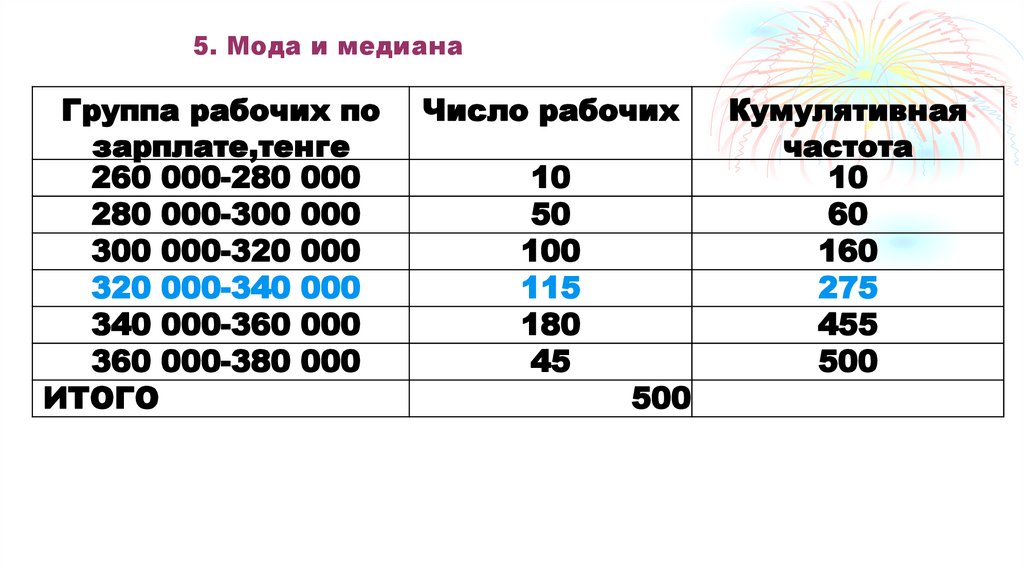
Группа рабочих по
зарплате,тенге
260 000-280 000
280 000-300 000
300 000-320 000
320 000-340 000
340 000-360 000
360 000-380 000
ИТОГО
Число рабочих
10
50
100
115
180
45
500
Кумулятивная
частота
10
60
160
275
455
500

80. 5. Мода и медиана

Ме= 320 000+ 20 000 * (500/2- 160)/115 =
320 000+20 000*0,78260=320 000+15652,2 =
=335 652,2 тенге.
т.е. у 50% рабочих средняя зарплата не
превышает 335 652,2 тенге.

81. 5. Мода и медиана

Квантили - величины, разделяющие
совокупность на определенное количество
равных по численности элементов частей.
Самый известный квантиль – медиана,
делящая совокупность на две равные
части.
Кроме медианы часто используются:
квартили, делящие ранжированный ряд
на 4 равные части,
децили -10 частей и
перцентили - на 100 частей.

82. 5. Мода и медиана

Квартили делят вариационный ранжированный
ряд на четыре равные части:
первый (нижний) квартиль (Q1) показывает
значение признака, которого не превышают
значения 25% единиц совокупности,
второй квартиль (Q2) совпадает с медианой
(Ме), т.е. 50% единиц совокупности по своему
значению меньше второго квартиля и 50%
больше него,
третий (верхний) квартиль (Q3) –значения
признака в совокупности, 75% единиц в которой
меньше его по своему значению.

83. 5. Мода и медиана

Деление ранжированного
равные части:
ряда
на
четыре
Второй квартиль совпадает с медианой, поэтому
на практике он никогда не рассчитывается.

84. 5. Мода и медиана

Децили (D) делят упорядоченную по возрастанию
значений признака совокупность на десять равных
частей:
первый дециль показывает значение признака,
которого
не
превышают
значения
10%
единиц
совокупности,
второй дециль - 20%,
третий дециль - 30% и т.д.
Пятый дециль совпадает с медианой и вторым
квартилем.

85. 5. Мода и медиана

Структурные показатели не зависят от
того,
имеются
ли
в
статистической
совокупности
аномальные
(резко
выделяющиеся) наблюдения или нет.
И если средняя величина при их наличии
теряет свою практическую значимость, то
информативность
медианы,
наоборот,
усиливается - она начинает выполнять
функции средней, то есть характеризовать
центр совокупности.

86. 5. Мода и медиана

87. 5. Мода и медиана

Например
Квартиль первый
Квартиль второй
Квартиль третий
Дециль первый
Дециль второй
Дециль третий
Дециль
четвертый
Дециль пятый
Дециль шестой

88. 5. Мода и медиана

89. 5. Мода и медиана

90. 5. Мода и медиана

Используя эту таблицу решим пример
Квартиль первый
Квартиль второй
Квартиль третий
Дециль первый
Дециль второй
Дециль третий
Дециль
четвертый
Дециль пятый
Дециль шестой

91. 5. Мода и медиана

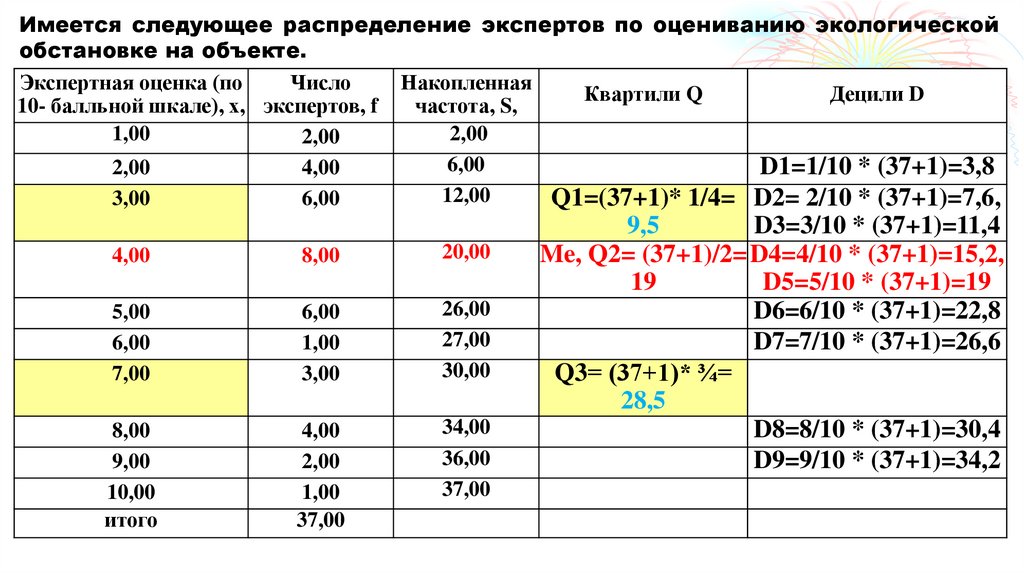
Имеется следующее распределение экспертов по оцениванию экологической
обстановке на объекте.
Экспертная оценка (по
Число
Накопленная
Квартили Q
Децили D
10- балльной шкале), х, экспертов, f
частота, S,
1,00
2,00
2,00
6,00
2,00
4,00
D1=1/10 * (37+1)=3,8
12,00
3,00
6,00
Q1=(37+1)* 1/4= D2= 2/10 * (37+1)=7,6,
4,00
8,00
20,00
5,00
6,00
7,00
6,00
1,00
3,00
26,00
27,00
30,00
8,00
9,00
10,00
итого
4,00
2,00
1,00
37,00
34,00
36,00
37,00
9,5
D3=3/10 * (37+1)=11,4
Me, Q2= (37+1)/2= D4=4/10 * (37+1)=15,2,
19
D5=5/10 * (37+1)=19
D6=6/10 * (37+1)=22,8
D7=7/10 * (37+1)=26,6
Q3= (37+1)* ¾=
28,5
D8=8/10 * (37+1)=30,4
D9=9/10 * (37+1)=34,2

92. 5. Мода и медиана

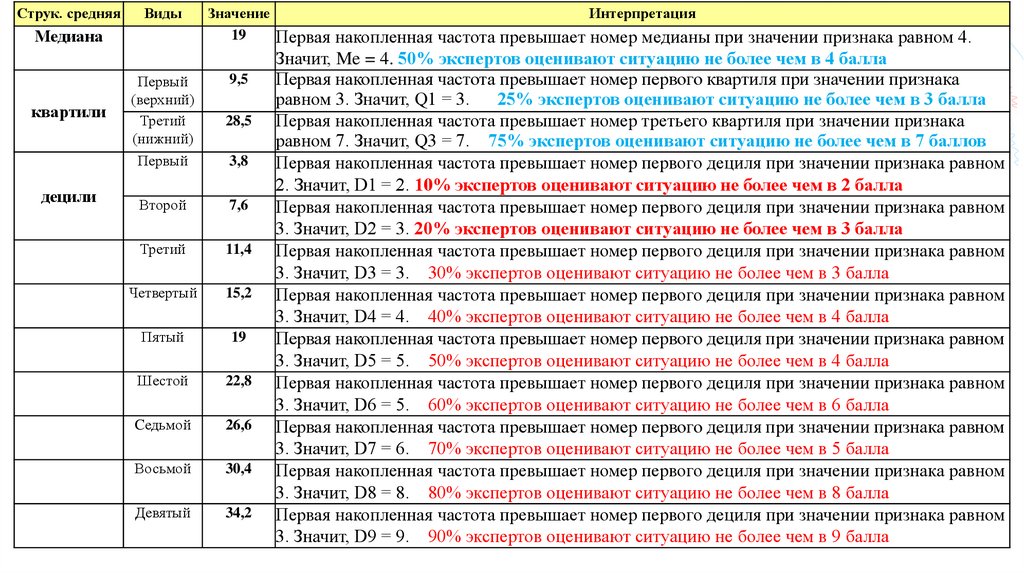
Струк. средняя
Виды
Медиана
квартили
децили
Значение
Интерпретация
19
Первая накопленная частота превышает номер медианы при значении признака равном 4.
Первый
(верхний)
Третий
(нижний)
Первый
28,5
Второй
7,6
Третий
11,4
Четвертый
15,2
Пятый
19
Шестой
22,8
Cедьмой
26,6
Восьмой
30,4
Девятый
34,2
9,5
3,8
Значит, Me = 4. 50% экспертов оценивают ситуацию не более чем в 4 балла
Первая накопленная частота превышает номер первого квартиля при значении признака
равном 3. Значит, Q1 = 3.
25% экспертов оценивают ситуацию не более чем в 3 балла
Первая накопленная частота превышает номер третьего квартиля при значении признака
равном 7. Значит, Q3 = 7. 75% экспертов оценивают ситуацию не более чем в 7 баллов
Первая накопленная частота превышает номер первого дециля при значении признака равном
2. Значит, D1 = 2. 10% экспертов оценивают ситуацию не более чем в 2 балла
Первая накопленная частота превышает номер первого дециля при значении признака равном
3. Значит, D2 = 3. 20% экспертов оценивают ситуацию не более чем в 3 балла
Первая накопленная частота превышает номер первого дециля при значении признака равном
3. Значит, D3 = 3. 30% экспертов оценивают ситуацию не более чем в 3 балла
Первая накопленная частота превышает номер первого дециля при значении признака равном
3. Значит, D4 = 4. 40% экспертов оценивают ситуацию не более чем в 4 балла
Первая накопленная частота превышает номер первого дециля при значении признака равном
3. Значит, D5 = 5. 50% экспертов оценивают ситуацию не более чем в 4 балла
Первая накопленная частота превышает номер первого дециля при значении признака равном
3. Значит, D6 = 5. 60% экспертов оценивают ситуацию не более чем в 6 балла
Первая накопленная частота превышает номер первого дециля при значении признака равном
3. Значит, D7 = 6. 70% экспертов оценивают ситуацию не более чем в 5 балла
Первая накопленная частота превышает номер первого дециля при значении признака равном
3. Значит, D8 = 8. 80% экспертов оценивают ситуацию не более чем в 8 балла
Первая накопленная частота превышает номер первого дециля при значении признака равном
3. Значит, D9 = 9. 90% экспертов оценивают ситуацию не более чем в 9 балла

93. 5. Мода и медиана

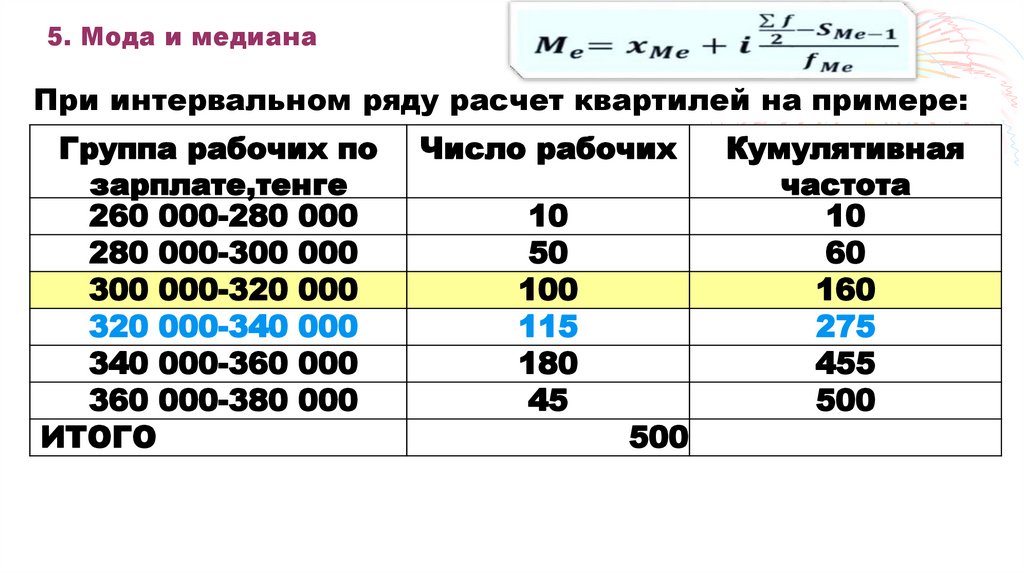
При интервальном ряду расчет квартилей на примере:
Группа рабочих по
зарплате,тенге
260 000-280 000
280 000-300 000
300 000-320 000
320 000-340 000
340 000-360 000
360 000-380 000
ИТОГО
Число рабочих
10
50
100
115
180
45
500
Кумулятивная
частота
10
60
160
275
455
500

94. 5. Мода и медиана

1) Ме= Q2 = 320 000+20 000* (500/2 – 160) /115 = 320 000+
(20 000*0,78260) = 320 000+15652,2 =335 652,2 тенге.
2) Для Q1 номер = ¼ *500 = 125
Q1 = 300 000+20 000* (¼*500 –60) /100 = 300 000+ (20 000*0,65)
= 313 000 тенге (25% имеют ЗП не превышающую 313
тыс.тенге).
3) Для Q3 номер = ¾ *500 = 375
Q1 =340 000+20 000*(¾*500 – 275) /180 =340 000+(20 000* 0,556)
= 351 111 тенге (75% имеют ЗП не превышающую 351,1
тыс.тенге).

95. 5. Мода и медиана

В
заключении,
приблизительное
равенство средней арифметической, моды
и медианы, рассчитанных по отношению к
одному и тому же ряду, говорит о том, что
значения
признака
в
изучаемой
совокупности имеют нормальный закон
распределения (или приближаются к нему).

96.

5. Мода и медиана
Таким образом, средние арифметическая
и
гармоническая
и
т.п.
(степенные
средние)
являются
обобщающими
характеристиками совокупности по тому
или иному варьирующему признаку.
Вспомогательными описательными характеристиками распределения варьирующего
признака служат мода и медиана.

97. 5. Мода и медиана

6. Основные правила применения средних в статистике
Средние должны относиться к явлениям
одного и того же вида и базироваться на
массовом обобщении фактов.
Только тогда они отражают сущность
явления и на их значение не оказывают
влияния случайные факторы.
Это требование в статистике связывает
средние с законом больших чисел.

98. 5. Мода и медиана

6. Основные правила применения средних в статистике
Второе требование к средним в статистике –
это требование качественной однородности
совокупности.
Оно состоит в том, что нельзя применять
средние к такой совокупности, отдельные
части которой подчинены различным законам
развития в отношении осредняемого признака.
Качественно
однородные
совокупности
выделяются с помощью метода группировки.

99.

6. Основные правила применения средних в статистике
Даже
в
пределах
однородной
совокупности количественные различия
могут
носить
не
случайный,
а
систематический характер.
Поэтому наряду с общей средней всей
совокупности
вычисляются
групповые
средние.

100.

6. Основные правила применения средних в статистике
Например, изучая динамику урожайности
сельскохозяйственных культур по стране
необходимо учитывать различие отдельных
районов по почвенным, климатическим и
другим условиям.
В этом случае динамика групповых
средних
более
полно
отразит
закономерности изменения урожайности,
чем общая средняя урожайность.

101.

6. Основные правила применения средних в статистике
Средние в статистике следует применять на
основе и в органическом единстве с
методом группировок.
Метод группировок позволяет:
- отграничить качественно однородные
совокупности для применения средних
характеристик,
- дополнить общую среднюю групповыми
средними,
-дополнить средние характеристики рядами
распределения.

102. 5. Мода и медиана

6. Основные правила применения средних в статистике
Не следует преувеличивать роль средних в
статистике. Часто, следуя за А. Кетле
статистику объявляют наукой о средних.
Преувеличивая роль средних, ряд ученых
при этом упрощенно подходят к средней, без
всякой попытки раскрыть ее природу, ее
качественное содержание.
Так, в среднем доходы населения могут
расти. В то же время может расти
неравенство в их распределении, и число
бедных,
имеющих
доходы
ниже
прожиточного минимума (43 407 в 2024году),
не уменьшаться.

103. 5. Мода и медиана

6. Основные правила применения средних в статистике
Следующая
тема
будет
посвящена
показателям вариации, то есть показателям, характеризующим отклонения от
средних величин.
Ряд из них, в частности, дисперсия и
среднее квадратическое отклонение, имеют
схожие
свойства
и
схожую
технику
вычислений, что и средняя арифметическая.
Они
существенно
увеличивают
возможности
анализа
рядов
распределения.

104. 5. Мода и медиана

Задания 1
Тарифный разряд рабочих
Число рабочих
2
8
3
16
Мода (с точностью до 0,1) равна:
A.3,9
B.3,6
C.2,0
D.4,0
E.5,0
4
17
5
12
6
7

105. 5. Мода и медиана

Задания 1
Тарифный разряд рабочих
Число рабочих
2
8
3
16
Мода (с точностью до 0,1) равна:
A.3,9
B.3,6
C.2,0
D.4,0
E.5,0
4
17
5
12
6
7

106. 6. Основные правила применения средних в статистике

Задания 2
Для значений признака: 3, 5, 6, 9, 11, 12, 13
Мода ...
A.13
B.9
C.16
D.отсутствует
E.5

107. 6. Основные правила применения средних в статистике

Задания 2
Для значений признака: 3, 5, 6, 9, 11, 12, 13
Мода ...
A.13
B.9
C.16
D.отсутствует
E.5

108. 6. Основные правила применения средних в статистике

Задания 3
Тарифный
рабочих
Число рабочих
разряд 2
3
4
5
6
18
16
7
12
7
Медиану (с точностью до 0,1) равна:
A.6
B.5
C.4
D.3
E.2

109. 6. Основные правила применения средних в статистике

Задания 3
Тарифный
рабочих
Число рабочих
разряд 2
3
4
5
6
18
16
7
12
7
Медиану (с точностью до 0,1) равна:
A.6
B.5
C.4
D.3
E.2

110. 6. Основные правила применения средних в статистике

Задания 4
Для следующих значений признака: 3, 3, 3, 4, 4,
6, 7, 9, 9 мода ...
A.3
B.4
C.6
D.8
E.9

111. 6. Основные правила применения средних в статистике

Задания 4
Для следующих значений признака: 3, 3, 3, 4, 4,
6, 7, 9, 9 мода ...
A.3
B.4
C.6
D.8
E.9

112. 6. Основные правила применения средних в статистике

Задача 1
По приведенным ниже данным о квалификации
рабочих цеха требуется:
1)построить дискретный ряд распределения;
2)дать графическое изображение ряда – полигон
распределения рабочих цеха по квалификации;
3)вычислить показатели центра распределения
(средняя арифметическая, мода и медиана),
показатели вариации и формы распределения.
Тарифные разряды 24 рабочих цеха: 4; 3; 6; 4; 4;
2; 3; 5; 4; 4; 5; 2; 3; 4; 4; 5; 2; 3; 6; 5; 4; 2; 4; 3.

113. Задания 1

114. Задания 1

Задача 2
Имеются следующие данные о возрастном составе
рабочих цеха (лет): 18; 38; 28; 29; 26; 38; 34; 22; 28; 30;
22; 23; 35; 33; 27; 24; 30; 32; 28; 25; 29; 26; 31; 24; 29; 27;
32; 25; 29; 29.
Для анализа распределения рабочих цеха по
возрасту требуется:
1)построить интервальный ряд распределения
(число групп 7);
2)дать графическое изображение ряда
(гистограмма и кумуляту);
3)исчислить показатели центра распределения,
показатели вариации и формы распределения.
Сформулировать вывод.

115. Задания 2

Конец презентации