Критерий Фридмана

1.

КРИТЕРИЙ ФРИДМАНА

2.

НАЗНАЧЕНИЕ КРИТЕРИЯ
ПРИМЕНЯЕТСЯ ДЛЯ СОПОСТАВЛЕНИЯ ПОКАЗАТЕЛЕЙ, ИЗМЕРЕННЫХ В ТРЕХ ИЛИ БОЛЕЕ
УСЛОВИЯХ НА ОДНОЙ И ТОЙ ЖЕ ВЫБОРКЕ ИСПЫТУЕМЫХ
ПОЗВОЛЯЕТ УСТАНОВИТЬ, ЧТО ВЕЛИЧИНЫ ПОКАЗАТЕЛЕЙ ОТ УСЛОВИЯ К УСЛОВИЮ
ИЗМЕНЯЮТСЯ, НО ПРИ ЭТОМ НЕ УКАЗЫВАЕТ НА НАПРАВЛЕНИЕ ИЗМЕНЕНИЙ
ЭМПИРИЧЕСКОЕ ЗНАЧЕНИЕ КРИТЕРИЯ УКАЗЫВАЕТ НА ТО, НАСКОЛЬКО РАЗЛИЧАЮТСЯ
СУММЫ РАНГОВ
ЧЕМ БОЛЬШЕ ЭМПИРИЧЕСКОЕ ЗНАЧЕНИЕ , ТЕМ БОЛЕЕ СУЩЕСТВЕННЫЕ
РАСХОЖДЕНИЯ СУММ РАНГОВ ОНО ОТРАЖАЕТ
ЕСЛИ РАВНЯЕТСЯ КРИТИЧЕСКОМУ ЗНАЧЕНИЮ ИЛИ ПРЕВЫШАЕТ ЕГО, РАЗЛИЧИЯ
СТАТИСТИЧЕСКИ ДОСТОВЕРНЫ

3.

ОГРАНИЧЕНИЯ КРИТЕРИЯ
НИЖНИЙ ПОРОГ: НЕ МЕНЕЕ 2-Х ИСПЫТУЕМЫХ (n>=2), КАЖДЫЙ ИЗ КОТОРЫХ ПРОШЕЛ
НЕ МЕНЕЕ 3-Х ЗАМЕРОВ (c>=З)
ПРИ с=3, n<=9, УРОВЕНЬ ЗНАЧИМОСТИ ПОЛУЧЕННОГО ЭМПИРИЧЕСКОГО ЗНАЧЕНИЯ
ОПРЕДЕЛЯЕТСЯ ПО ТАБЛИЦЕ VII-A ПРИЛОЖЕНИЯ 1 (ПО УЧЕБНИКУ Е.В. СИДОРЕНКО)
ПРИ с=4, n<=4, УРОВЕНЬ ЗНАЧИМОСТИ ПОЛУЧЕННОГО ЭМПИРИЧЕСКОГО ЗНАЧЕНИЯ
ОПРЕДЕЛЯЕТСЯ ПО ТАБЛИЦЕ VII-Б ПРИЛОЖЕНИЯ 1 (ПО УЧЕБНИКУ Е.В. СИДОРЕНКО)
ПРИ БОЛЬШИХ КОЛИЧЕСТВАХ ИСПЫТУЕМЫХ ИЛИ УСЛОВИЙ ПОЛУЧЕННЫЕ
ЭМПИРИЧЕСКИЕ ЗНАЧЕНИЯ СОПОСТАВЛЯЮТСЯ С КРИТИЧЕСКИМИ ЗНАЧЕНИЯМИ ,
ОПРЕДЕЛЯЕМЫМИ ПО ТАБЛИЦЕ IX ПРИЛОЖЕНИЯ 1 (ПО УЧЕБНИКУ Е.В. СИДОРЕНКО)
ИМЕЕТ РАСПРЕДЕЛЕНИЕ, СХОДНОЕ С РАСПРЕДЕЛЕНИЕМ . ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ v
ОПРЕДЕЛЯЕТСЯ ПО ФОРМУЛЕ:
v=c-1, ГДЕ c – КОЛИЧЕСТВО УСЛОВИЙ ИЗМЕРЕНИЯ (ЗАМЕРОВ)

4.

СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ
Н0: МЕЖДУ ПОКАЗАТЕЛЯМИ, ПОЛУЧЕННЫМИ (ИЗМЕРЕННЫМИ) В РАЗНЫХ УСЛОВИЯХ,
СУЩЕСТВУЮТ ЛИШЬ СЛУЧАЙНЫЕ РАЗЛИЧИЯ
Н1: МЕЖДУ ПОКАЗАТЕЛЯМИ, ПОЛУЧЕННЫМИ (ИЗМЕРЕННЫМИ) В РАЗНЫХ УСЛОВИЯХ,
СУЩЕСТВУЮТ НЕСЛУЧАЙНЫЕ РАЗЛИЧИЯ
Н0: р>0,05
H1: р<=0,05
H1: р<=0,01

5.

ЗАДАЧА
ЭКСПЕРИМЕНТАТОР ИССЛЕДОВАЛ ЛАБИЛЬНОСТЬ МЫШЛЕНИЯ У ИСПЫТУЕМЫХ МЕТОДОМ
РЕШЕНИЯ АНАГРАММ. АНАГРАММЫ БЫЛИ ПОДОБРАНЫ ТАКИМ ОБРАЗОМ, ЧТО
ЭКСПЕРИМЕНТАТОР ПОСТЕПЕННО ГОТОВИЛ ИСПЫТУЕМОГО К САМОЙ ТРУДНОЙ (А
ФАКТИЧЕСКИ НЕРАЗРЕШИМОЙ) ЗАДАЧЕ. ИНЫМ СЛОВАМИ, ИСПЫ ТУЕМЫЙ ДОЛЖЕН БЫЛ
ПОСТЕПЕННО ПРИВЫКНУТЬ К ТОМУ, ЧТО ЗАДАЧИ СТАНОВЯТСЯ ВСЕ БОЛЕЕ И БОЛЕЕ
ТРУДНЫМИ, И ЧТО НАД КАЖДОЙ ПОСЛЕДУЮЩЕЙ АНАГРАММОЙ ЕМУ ПРИХОДИТСЯ
ПРОВОДИТЬ БОЛЬШЕ ВРЕМЕНИ.
СНАЧАЛА ИСПЫТУЕМОМУ ПРЕДЛАГАЛОСЬ СЛОЖИТЬ СЛОВО ИЗ 4 БУКВ
ЗАТЕМ ИЗ 5 БУКВ
ЗАТЕМ ИЗ 6 БУКВ
ВОПРОС: ДОСТОВЕРНЫ ЛИ РАЗЛИЧИЯ ВО ВРЕМЕНИ РЕШЕНИЯ ИСПЫТУЕМЫМИ
АНАГРАММ?

6.

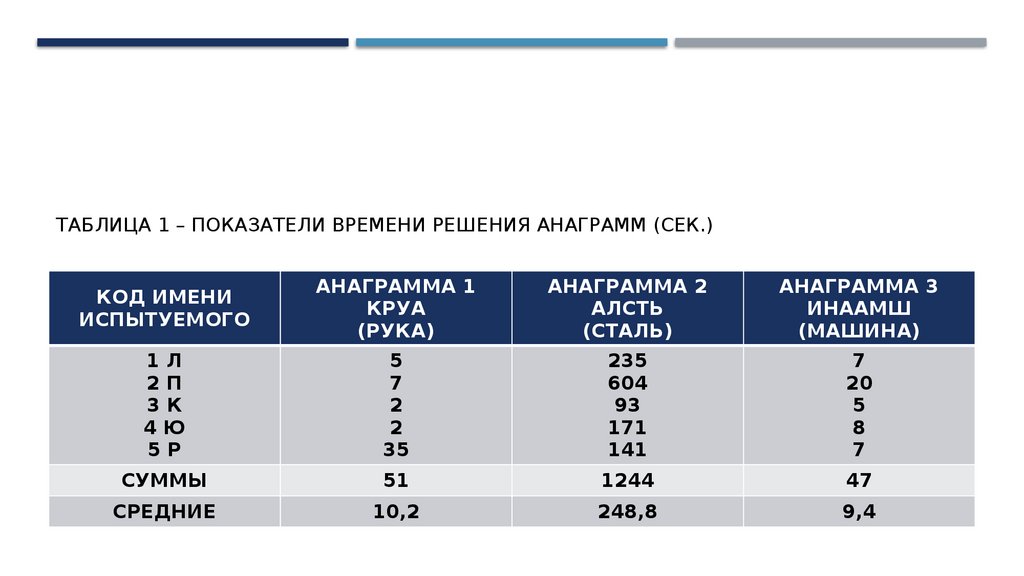
ЗАДАЧА
ТАБЛИЦА 1 – ПОКАЗАТЕЛИ ВРЕМЕНИ РЕШЕНИЯ АНАГРАММ (СЕК.)
КОД ИМЕНИ
ИСПЫТУЕМОГО
АНАГРАММА 1
КРУА
(РУКА)
АНАГРАММА 2
АЛСТЬ
(СТАЛЬ)
АНАГРАММА 3
ИНААМШ
(МАШИНА)
1Л
2П
3К
4Ю
5Р
5
7
2
2
35
235
604
93
171
141
7
20
5
8
7
СУММЫ
51
1244
47
СРЕДНИЕ
10,2
248,8
9,4

7.

ПРАВИЛА
РАНЖИРОВАНИЕ ВСЕГДА ПРОВОДИТСЯ ПО ГОРИЗОНТАЛИ В ПРЕДЕЛАХ КАЖДОГО
ИСПЫТУЕМОГО ОТДЕЛЬНО
РАНГИ ПРИСВАИВАЮТСЯ ОТ МЕНЬШЕГО ЗНАЧЕНИЯ К БОЛЬШЕМУ ЗНАЧЕНИЮ
АЛГОРИТМ РАСЧЕТА СМОТРИ В ПРИЛОЖЕННОМ ДОКУМЕНТЕ

8.

РУЧНОЙ АЛГОРИТМ РАСЧЕТА
СТРОИМ ТАБЛИЦУ 2 (ПРИЛОЖЕННЫЙ ДОКУМЕНТ) – ЭТО БУДУТ ПОКАЗАТЕЛИ ВРЕМЕНИ
РЕШЕНИЯ АНАГРАММ 1,2,3 И ИХ РАНГИ (n=5)
ДЛЯ ЭТОГО РАНЖИРУЕМ ЗНАЧЕНИЯ, ПОЛУЧЕННЫЕ ПО ТРЕМ АНАГРАММАМ КАЖДЫМ
ИСПЫТУЕМЫМ
НАПРИМЕР, ИСПЫТУЕМЫЙ К МЕНЬШЕ ВСЕГО ВРЕМЕНИ ПРОВЕЛ НАД АНАГРАММОЙ 1 –
СЛЕДОВАТЕЛЬНО, ОНА ПОЛУЧАЕТ РАНГ 1. НА ВТОРОМ МЕСТЕ У НЕГО СТОИТ АНАГРАММА
3 – ОНА ПОЛУЧАЕТ РАНГ 2. НАКОНЕЦ, АНАГРАММА 2 ПОЛУЧАЕТ РАНГ 3, ПОТОМУ ЧТО ОНА
РЕШАЛАСЬ ИМ ДОЛЬШЕ ДВУХ ДРУГИХ
СУММА РАНГОВ ПО КАЖДОМУ ИСПЫТУЕМОМУ ДОЛЖНА СОСТАВЛЯТЬ 6
ПОДСЧИТЫВАЕМ СУММУ РАНГОВ ПО КАЖДОЙ АНАГРАММЕ (6,15,9)
НАХОДИМ ОБЩУЮ СУММУ РАНГОВ: 6+15+9=30
НАХОДИМ РАСЧЕТНУЮ СУММУ РАНГОВ ПО ФОРМУЛЕ
РАВЕНСТВО РЕАЛЬНОЙ И РАСЧЕТНОЙ СУММ СОБЛЮДЕНО

9.

СФОРМУЛИРУЕМ СТАТИСТИЧЕСКИЕ
ГИПОТЕЗЫ
Н0: РАЗЛИЧИЯ ВО ВРЕМЕНИ, КОТОРОЕ ИСПЫТУЕМЫЕ ПРОВОДЯТ НАД РЕШЕНИЕМ ТРЕХ
РАЗЛИЧНЫХ АНАГРАММ, ЯВЛЯЮТСЯ СЛУЧАЙНЫМИ
Н1: РАЗЛИЧИЯ ВО ВРЕМЕНИ, КОТОРОЕ ИСПЫТУЕМЫЕ ПРОВОДЯТ НАД РЕШЕНИЕМ ТРЕХ
РАЗЛИЧНЫХ АНАГРАММ, НЕ ЯВЛЯЮТСЯ СЛУЧАЙНЫМИ

10.

ИСПОЛЬЗОВАНИЕ ФОРМУЛЫ
ОПРЕДЕЛИМ ЭМПИРИЧЕСКОЕ ЗНАЧЕНИЕ ПО ФОРМУЛЕ:

11.

ИСПОЛЬЗОВАНИЕ ТАБЛИЦЫ
ПОСКОЛЬКУ В ДАННОМ ПРИМЕРЕ РАССМАТРИВАЮТСЯ ТРИ ЗАДАЧИ, ТО ЕСТЬ 3 УСЛОВИЯ,
с=3. КОЛИЧЕСТВО ИСПЫТУЕМЫХ n=5
ЭТО ПОЗВОЛЯЕТ НАМ ВОСПОЛЬЗОВАТЬСЯ СПЕЦИАЛЬНОЙ ТАБЛИЦЕЙ , А ИМЕННО
ТАБЛИЦЕЙ VII-A ПРИЛОЖЕНИЯ 1 (ПО УЧЕБНИКУ Е.В. СИДОРЕНКО, ПРИЛОЖЕННЫЙ
ДОКУМЕНТ)
ПО НЕЙ ЭМПИРИЧЕСКОЕ ЗНАЧЕНИЕ =8,4 ПРИ c=3, n=5 ТОЧНО СООТВЕТСТВУЕТ УРОВНЮ
ЗНАЧИМОСТИ p=0,0085.
p 0,01

12.

РЕШЕНИЕ ЗАДАЧИ
ОТВЕТ: Н0 ОТКЛОНЯЕТСЯ. ПРИНИМАЕТСЯ Н1. РАЗЛИЧИЯ ВО ВРЕМЕНИ, КОТОРОЕ
ИСПЫТУЕМЫЕ ПРОВОДЯТ НАД РЕШЕНИЕМ ТРЕХ РАЗЛИЧНЫХ АНАГРАММ, НЕСЛУЧАЙНЫ
(p=0,0085<p=0,01).

13.

АЛГОРИТМ РАСЧЕТА В ПРОГРАММЕ
SPSS
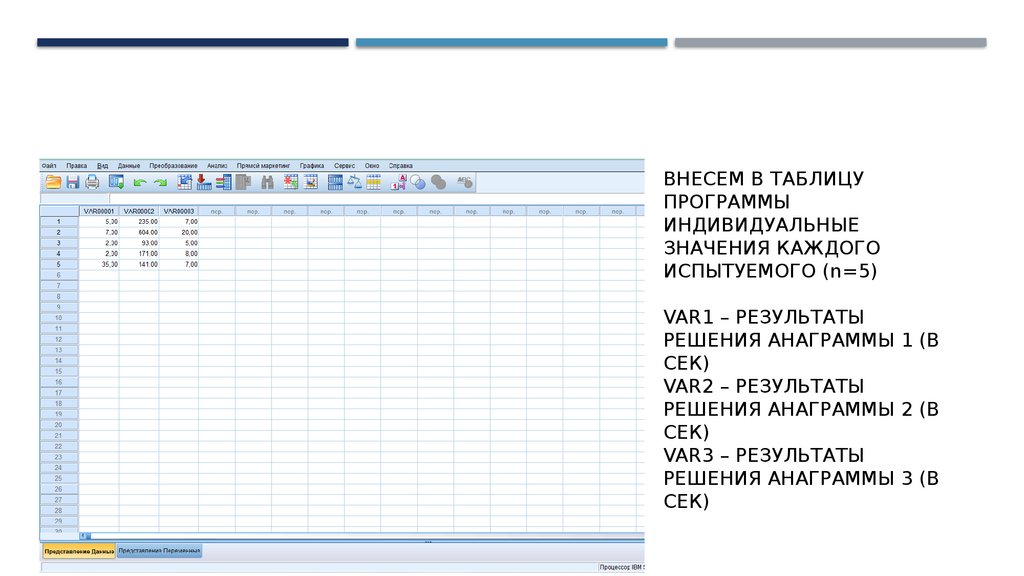
ВНЕСЕМ В ТАБЛИЦУ
ПРОГРАММЫ
ИНДИВИДУАЛЬНЫЕ
ЗНАЧЕНИЯ КАЖДОГО
ИСПЫТУЕМОГО (n=5)
VAR1 – РЕЗУЛЬТАТЫ
РЕШЕНИЯ АНАГРАММЫ 1 (В
СЕК)
VAR2 – РЕЗУЛЬТАТЫ
РЕШЕНИЯ АНАГРАММЫ 2 (В
СЕК)
VAR3 – РЕЗУЛЬТАТЫ
РЕШЕНИЯ АНАГРАММЫ 3 (В
СЕК)

14.

АЛГОРИТМ РАСЧЕТА В ПРОГРАММЕ
SPSS
ЗАХОДИМ ВО ВКЛАДКУ
«ПРЕДСТАВЛЕННЫЕ ПЕРЕМЕННЫЕ»
ВНИЗУ ТАБЛИЦЫ
ВО ВКЛАДКЕ «МЕРА» МЕНЯЕМ ТИП
ШКАЛЫ ВНЕСЕННЫХ НАМИ ДАННЫХ
НА ПОРЯДКОВУЮ

15.

АЛГОРИТМ РАСЧЕТА В ПРОГРАММЕ
SPSS
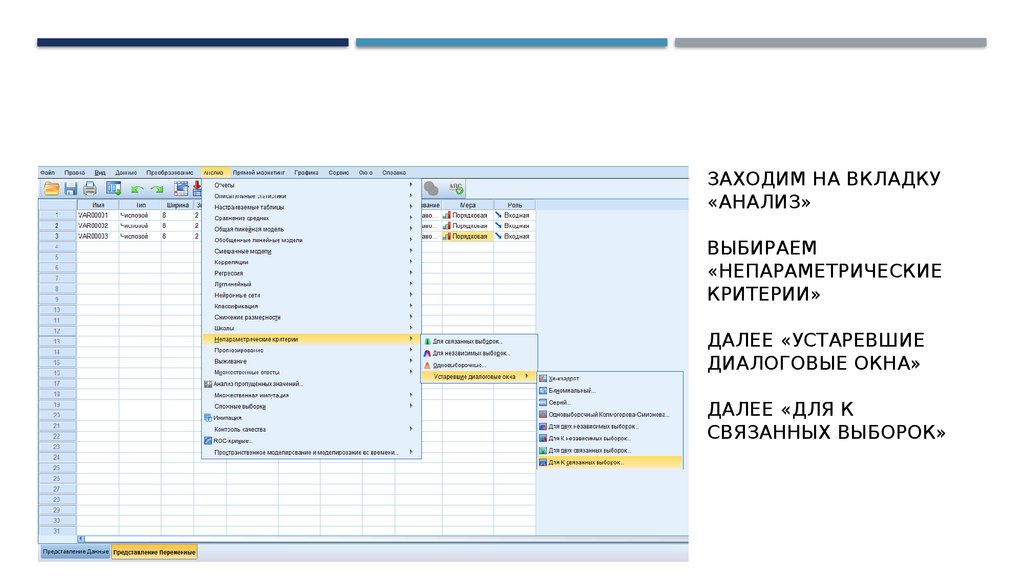
ЗАХОДИМ НА ВКЛАДКУ
«АНАЛИЗ»
ВЫБИРАЕМ
«НЕПАРАМЕТРИЧЕСКИЕ
КРИТЕРИИ»
ДАЛЕЕ «УСТАРЕВШИЕ
ДИАЛОГОВЫЕ ОКНА»
ДАЛЕЕ «ДЛЯ К
СВЯЗАННЫХ ВЫБОРОК»

16.

АЛГОРИТМ РАСЧЕТА В ПРОГРАММЕ
SPSS
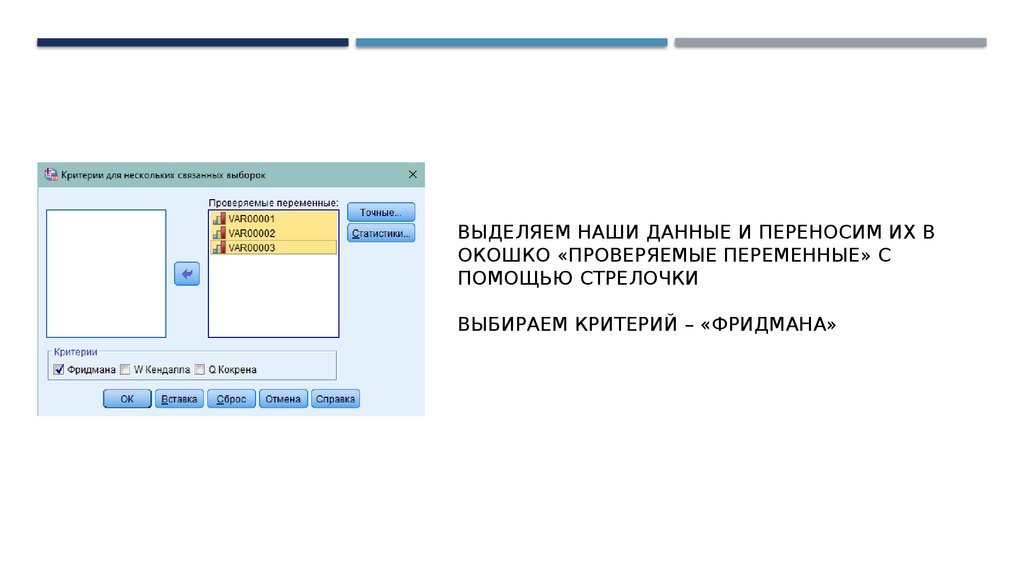
ВЫДЕЛЯЕМ НАШИ ДАННЫЕ И ПЕРЕНОСИМ ИХ В
ОКОШКО «ПРОВЕРЯЕМЫЕ ПЕРЕМЕННЫЕ» С
ПОМОЩЬЮ СТРЕЛОЧКИ
ВЫБИРАЕМ КРИТЕРИЙ – «ФРИДМАНА»

17.

АЛГОРИТМ РАСЧЕТА В ПРОГРАММЕ
SPSS
СМОТРИМ НА НАШИ РЕЗУЛЬТАТЫ
НАС ИНТЕРЕСУЕТ ЗНАЧЕНИЕ «ХИ-КВАДРАТ» – ОНО
СОВПАДАЕТ С НАШИМИ РУЧНЫМИ РАСЧЕТАМИ
ОБРАТИМ ВНИМАНИЕ НА «АСИМПТОТИЧЕСКУЮ
ЗНАЧИМОСТЬ» – ЭТО И ЕСТЬ УРОВЕНЬ ЗНАЧИМОСТИ
(p=0,015)
ТАКИМ ОБРАЗОМ, ЗАДАЧА РЕШЕНА ВЕРНО

18.

ЗАДАЧА ДЛЯ ЗАКРЕПЛЕНИЯ
В ИССЛЕДОВАНИИ Г.А. БАДАСОВОЙ БЫЛО УСТАНОВЛЕНО, ЧТО ИСПЫТУЕМЫЕ ПОРАЗНОМУ ОТНОСЯТСЯ К НАКАЗАНИЯМ, КОТОРЫЕ СОВЕРШАЮТ ПО ОТНОШЕНИЮ К ДЕТЯМ
РАЗНЫ ЛЮДИ. НАПРИМЕР, НАКАЗАНИЯ СО СТОРОНЫ САМОГО РОДИТЕЛЯ СЧИТАЕТСЯ
БОЛЕЕ ПРИЕМЛЕМЫМ, ЧЕМ НАКАЗАНИЕ СО СТОРОНЫ БАБУШКИ, И ТЕМ БОЛЕЕ
ВОСПИТАТЕЛЬНИЦЫ ИЛ УЧИТЕЛЬНИЦЫ (СМ. ТАБЛИЦУ 4 В ПРИЛОЖЕННОМ ДОКУМЕНТЕ).
МОЖНО ЛИ ГОВОРИТЬ О ДОСТОВЕРНОЙ ТЕНДЕНЦИИ В ОЦЕНКАХ?
ДЛЯ РЕШЕНИЯ ЗАДАЧИ ПОНАДОБЯТСЯ ТАБЛИЦЫ 4 И 5 (СМ. ПРИЛОЖЕННЫЙ ДОКУМЕНТ)

19.

ЛИТЕРАТУРА
НАСЛЕДОВ А.Д. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ПСИХОЛОГИЧЕСКОГО ИССЛЕДОВАНИЯ.
АНАЛИЗ И ИНТЕРПРЕТАЦИЯ ДАННЫХ. УЧЕБНОЕ ПОСОБИЕ. – СПБ.: РЕЧЬ, 2004. – 392 С.
СИДОРЕНКО Е.В. МЕТОДЫ МАТЕМАТИЧЕСКОЙ ОБРАБОТКИ В ПСИХОЛОГИИ. – СПБ.: РЕЧЬ,
2000. – 350 С.