Похожие презентации:
Производная функции. Тема 9
1.
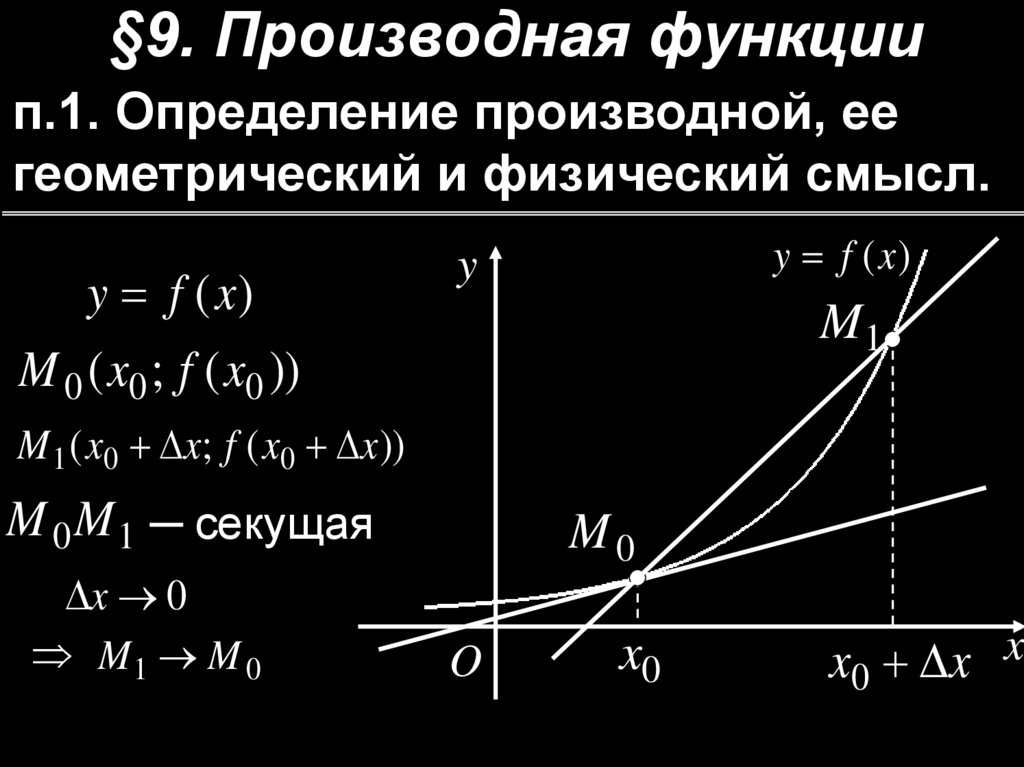
§9. Производная функциип.1. Определение производной, ее
геометрический и физический смысл.
y f (x )
M 0 ( x0 ; f ( x0 ))
y f (x )
y
M1
M 1 ( x0 x; f ( x0 x ))
M 0 M 1 ─ секущая
x 0
M1 M 0
M0
O
x0
x0 x x
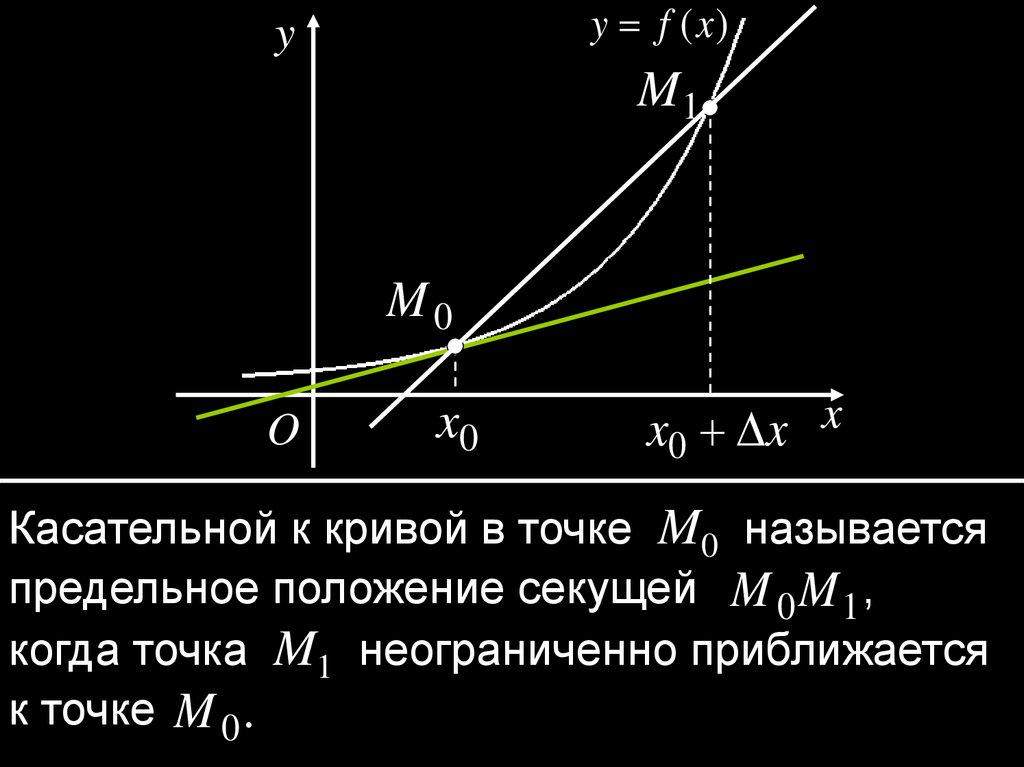
2.
y f (x )y
M1
M0
O
x0
x0 x x
Касательной к кривой в точке M0 называется
предельное положение секущей M 0 M 1 ,
когда точка M1 неограниченно приближается
к точке M 0 .
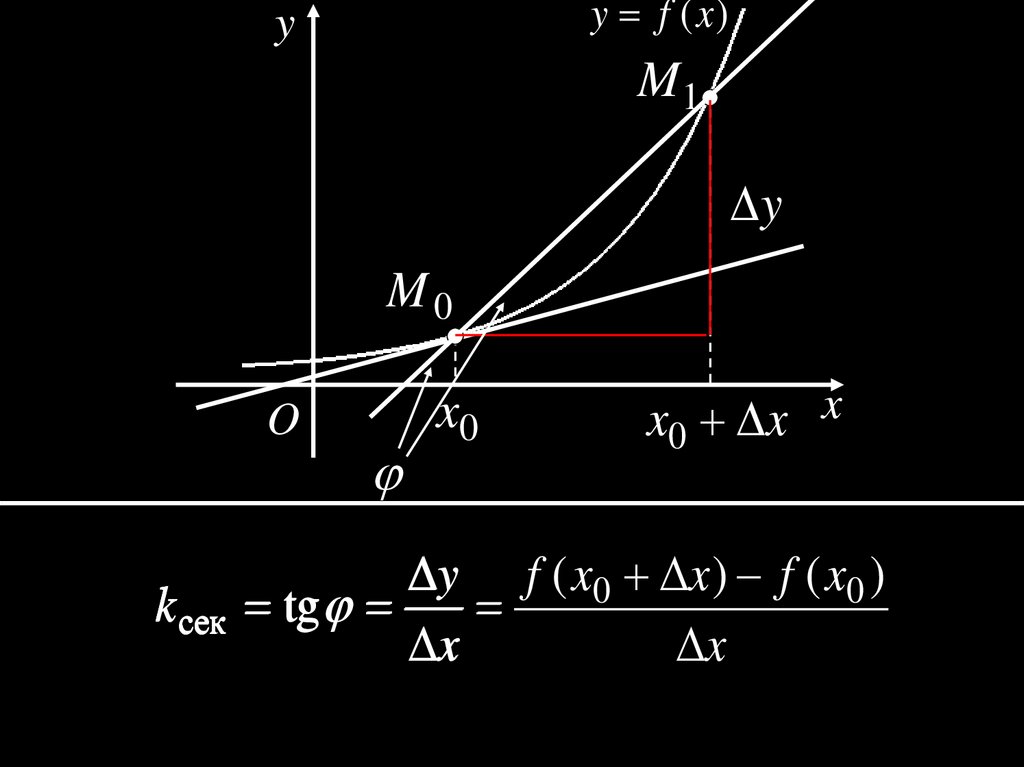
3.
y f (x )y
M1
y
M0
O
x0
x0 x x
y f ( x0 x ) f ( x0 )
k сек tg
x
x
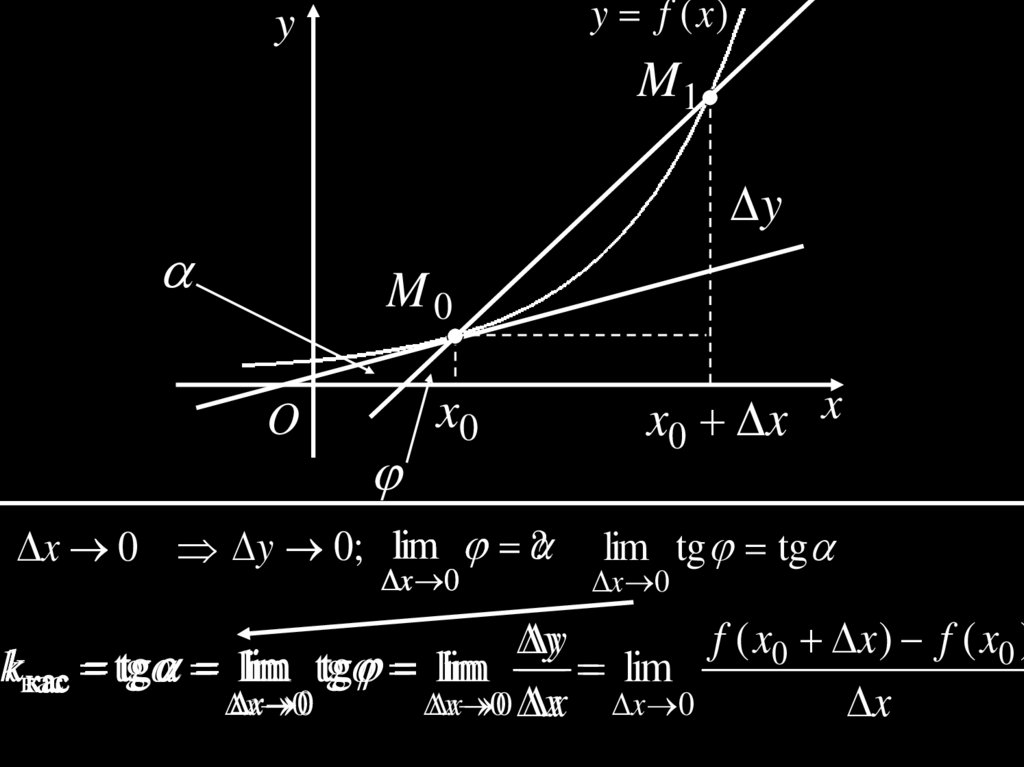
4.
y f (x )y
M1
y
M0
O
x0
?
x 0 y 0; lim
x 0
x0 x x
lim tg tg
x 0
f ( x0 x ) f ( x 0 )
yy
kkкас
tg
tg lim
lim tg
tg lim
lim
lim
кас
xx
00
xx
00
xx x 0
x
5.
Производной функции y f (x ) в точке x0называется предел отношения приращения
функции к приращению аргумента, когда
приращение аргумента стремится к нулю.
f ( x0 x ) f ( x 0 )
f ' ( x0 ) lim
x 0
x
f ( x ) f ( x0 )
f ' ( x0 ) lim
x x0
x x0
6.
Физический смыслЕсли функция y f (x ) описывает какой-либо
физический процесс, то производная y есть
скорость протекания этого процесса.
s s (t )
s ' (t ) v (t )
7.
Геометрический смыслy
k кас lim
f ' ( x0 )
x 0 x
Производная f ' ( x0 ) в точке x0 равна
угловому коэффициенту касательной к
графику функции в точке с абсциссой x0 .
Уравнение касательной
y f ' ( x0 )( x x0 ) f ( x0 )
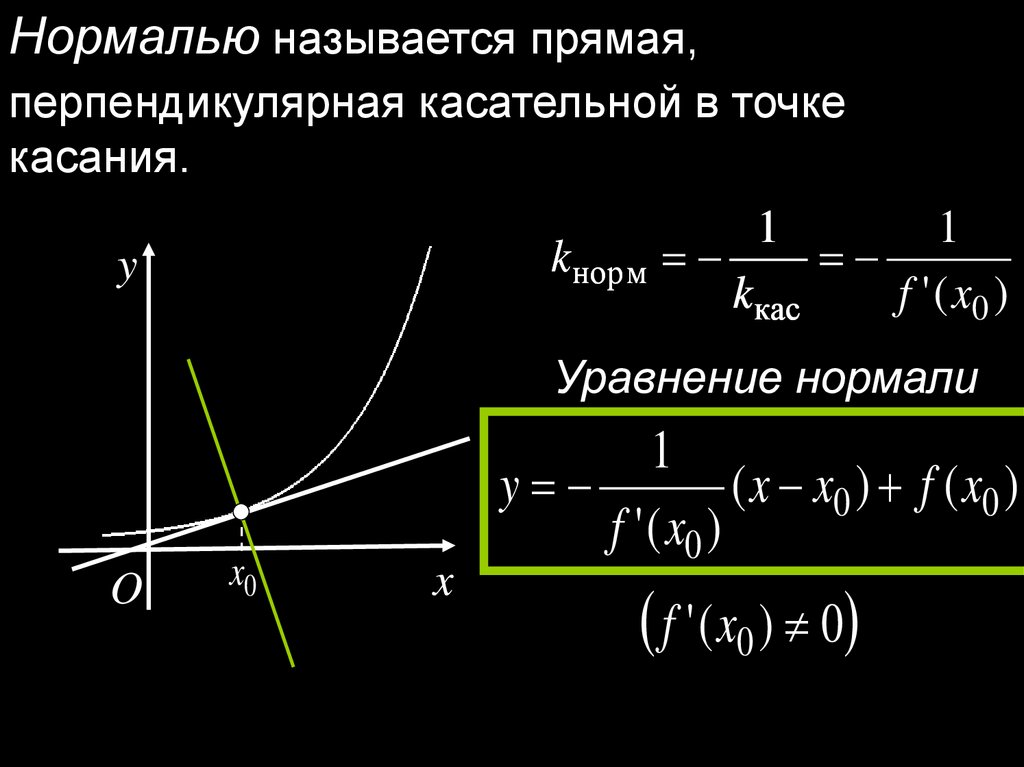
8.
Нормалью называется прямая,перпендикулярная касательной в точке
касания.
1
1
k норм
k кас
f ' ( x0 )
y
Уравнение нормали
O
x0
x
1
y
( x x0 ) f ( x0 )
f ' ( x0 )
f ' ( x0 ) 0
9.
п.2. Связь между существованиемпроизводной и непрерывностью.
Теорема 1. Если функция y f (x ) в точке x0
имеет производную, то она
непрерывна в этой точке.
10.
Доказательство.Теорема 2 из §6
y
f ' ( x0 ) lim
x 0 x
y
f ' ( x0 ) ( x )
x
(x ) ─ БМФ при x 0
y f ' ( x0 ) x ( x ) x
lim y lim f ' ( x0 ) x ( x ) x
x 0
x 0
f ' ( x0 ) lim x lim ( x ) x 0
x 0
x 0
y f (x ) непрерывна в точке x0 .
11.
Замечание. Обратное утверждение неверно.Пример.
y | x |
x0 0
y
O
y | x |
x
y f (0 x ) f (0) f ( x ) | x | 1, x 0;
x
x
x
x 1, x 0.
12.
yВывод: предел отношения
в точке x0 0
x
не существует.
Значит, функция y | x | непрерывна в точке
, но неxимеет
0 0 в этой точке производной.
График этой функции не имеет касательной в
точке O ( 0;0).
13.
п.3. Правила дифференцирования(нахождения производной).
Теорема 2. Если функции u u (x ) и v v (x )
в точке x имеют производную, то их сумма,
разность, произведение и частное также
имеют производную в этой точке (частное при
условии v ( x ) 0 ), причем справедливы
формулы:
(u v ) u v
(u v ) u v u v
u u v u v
2
v
v
14.
Доказательство.u ( x x ) v ( x x ) u ( x ) v ( x )
(u ( x ) v ( x )) lim
x 0
x
u ( x x ) u ( x ) v ( x x ) v ( x )
lim
x 0
x
u ( x x ) u ( x ) v ( x x ) v ( x )
lim
x 0
x
x
u ( x x ) u ( x )
v ( x x ) v ( x )
lim
lim
x 0
x 0
x
x
u ( x ) v ( x )
15.
u ( x x ) v ( x x ) u ( x ) v ( x )(u ( x ) v ( x )) lim
x 0
x
u ( x x ) v ( x x ) u ( x ) v ( x x ) u ( x ) v ( x x ) u ( x ) v ( x )
lim
x 0
x
u ( x x ) u ( x ) v ( x x ) u ( x ) v ( x x ) v ( x )
lim
x 0
x
v ( x x ) v ( x )
u ( x x ) u ( x )
lim
v ( x x ) u ( x )
x 0
x
x
u ( x x ) u ( x )
v ( x x ) v ( x )
lim
lim v ( x x ) lim u ( x ) lim
x 0
x 0
x 0
x 0
x
x
u ( x ) v ( x ) u ( x ) v ( x )
16.
Самостоятельно: доказать формулы дляпроизводной разности и частного двух
функций.
17.
п.4. Вывод таблицы производных.Производная обратной и сложной
функции.
1.
f ( x) C
f ( x x ) f ( x )
C C
f ' ( x ) lim
lim
0
x 0
x 0 x
x
(C ) 0
18.
2.f ( x ) sin x
sin( x x ) sin x
f ' ( x ) lim
x 0
x
x
x
2 sin
cos x
2
2
lim
x 0
x
x
2 sin
x
2
lim
lim cos x 1 cos x cos x
x 0
x 0
x
2
(sin x ) cos x
19.
3.f ( x ) cos x
(cos x ) sin x
Доказать самостоятельно.
20.
4.f ( x ) tg x
sin x (sin x )' cos x (cos x )' sin x
(tg x )
2
cos
x
cos x
cos x sin x
2
2
2
cos x
( tg x)
1
2
cos x
1
2
cos x
21.
5.f ( x ) ctg x
(ctg x)
1
2
sin x
Доказать самостоятельно.
22.
6. f ( x ) a( a ) lim
x
x
a
x x
x 0
lim a lim
x
x 0
x
a
a a 1
lim
x 0
x
x
x 0
x
a
x
x
1
x
a ln a
x
( a ) a ln a
x
x
23.
7. f ( x ) ex
(e ) e
x
x
Доказать самостоятельно.
24.
Теорема 3. Если функция y f (x ) строгомонотонна и непрерывна в
некоторой окрестности точки x0 ,
имеет производную в точке x0
и f ' ( x0 ) 0, то обратная функция
1
имеет производную
x f ( y) в
соответствующей точке
,
, причем
y0 y 0 f ( x 0 )
(f
1
1
( y 0 ))
f ' ( x0 )
25.
Доказательство.x f
1
монотонна
и
непрерывна
( y)
в некоторой окрестности точки y0
y 0 x 0
f
1
y 0 x 0
x
1
1
( y0 ) lim
lim
y
y 0 y y 0 y
lim
x x 0 x
1
f ' ( x0 )
'
26.
8. f ( x ) log a xa 0, a 1
y
x a
1
log a x ' y
y
x
ln
a
a
ln
a
a
'
1
1
Теорема 3
1
log a x
x ln a
'
27.
9.f ( x ) ln x
1
ln x
x
'
Доказать самостоятельно.
28.
10. f ( x ) arcsin xx sin y
x [ 1;1] y ;
2 2
1
1
arcsin x
'
sin y cos y 1 sin 2 y
1
2
1 x
1
'
arcsin x
2
1 x
'
1
29.
11. f ( x ) arccos xarccos x
'
Доказать самостоятельно.
1
1 x
2
30.
12.f ( x ) arctg x
arctg x
1
'
1 x
Доказать самостоятельно.
2
31.
13. f ( x ) arcctg xarcctg x
1
'
1 x
Доказать самостоятельно.
2
32.
Теорема 4. Если функция u (x ) имеет вточке x0 производную ' ( x0 ),
а функция y f (u ) имеет
в точке u0 , u 0 ( x0 ),
производную f ' (u 0 ) ,
то сложная функция y f ( ( x ))
имеет производную в точке x0
и справедлива формула:
y ' ( x0 ) f ' (u 0 ) ' ( x0 ).
33.
Доказательство.Теорема 2 из §6
f (u 0 )
f ' (u0 ) lim
u 0 u
f
(
u
)
0
f ' (u 0 ) ( u )
u
( u ) ─ БМФ при u 0
f (u 0 ) f ' (u 0 ) u ( u ) u : x
f (u 0 )
u
u
f ' (u 0 )
( u )
x
x
x
34.
f (u 0 )u
u
f ' (u 0 )
( u )
x
x
x
f ( ( x0 ))
f (u 0 )
'
f ( ( x0 )) lim
lim
x 0
x 0 x
x
u
u
lim f ' (u0 )
( u )
x 0
x
x
u
u
f ' (u0 ) lim
lim ( u ) lim
x 0 x x 0
x 0 x
f ' (u 0 ) ' ( x0 ) 0 ' ( x 0 ) f ' (u 0 ) ' ( x0 )
35.
14. f ( x ) xx e
ln x
e
x e e
'
ln x '
ln x
ln x
ln x
1
1
1
x x
x
x
ln x
e
'
x x
'
1









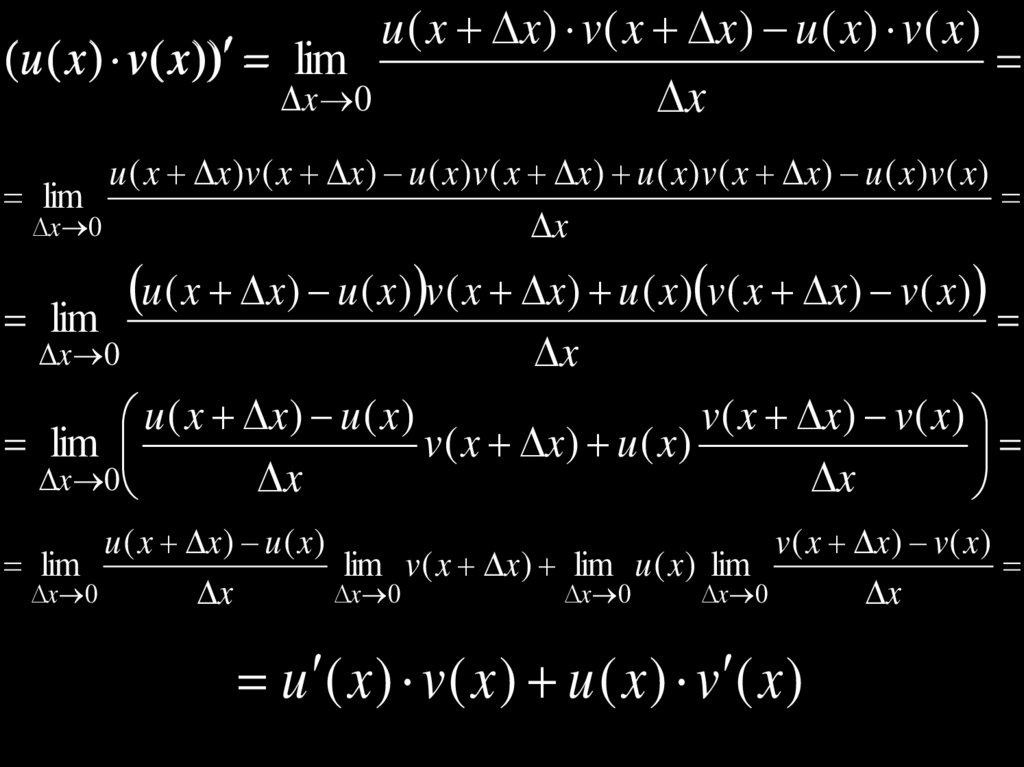


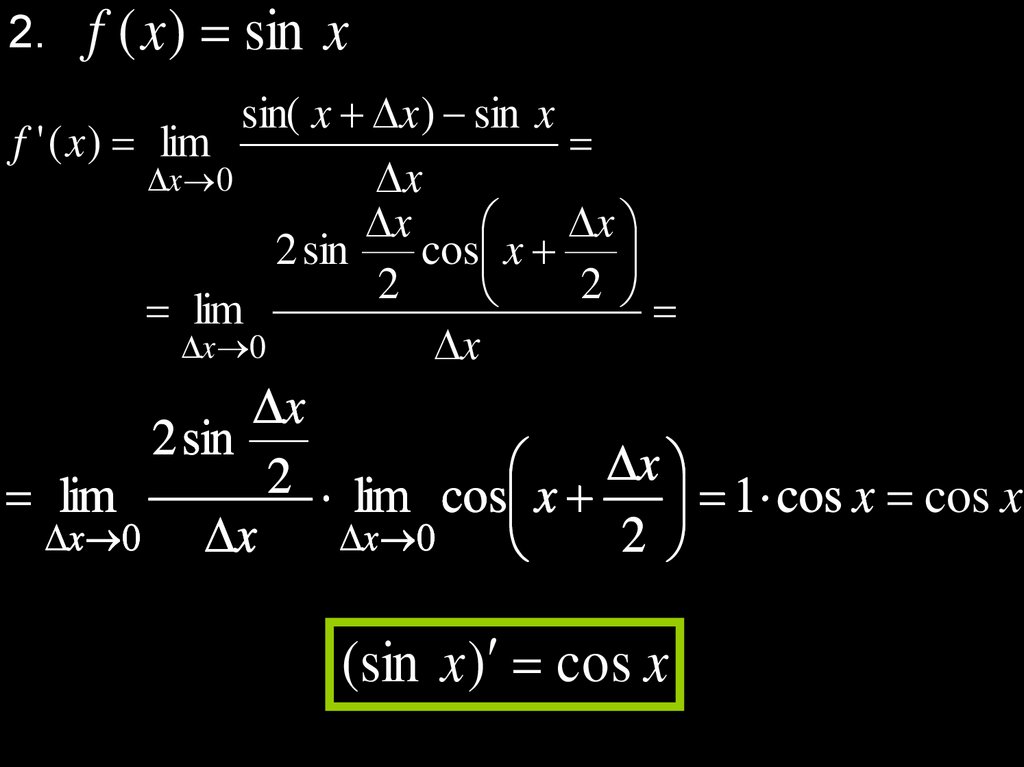

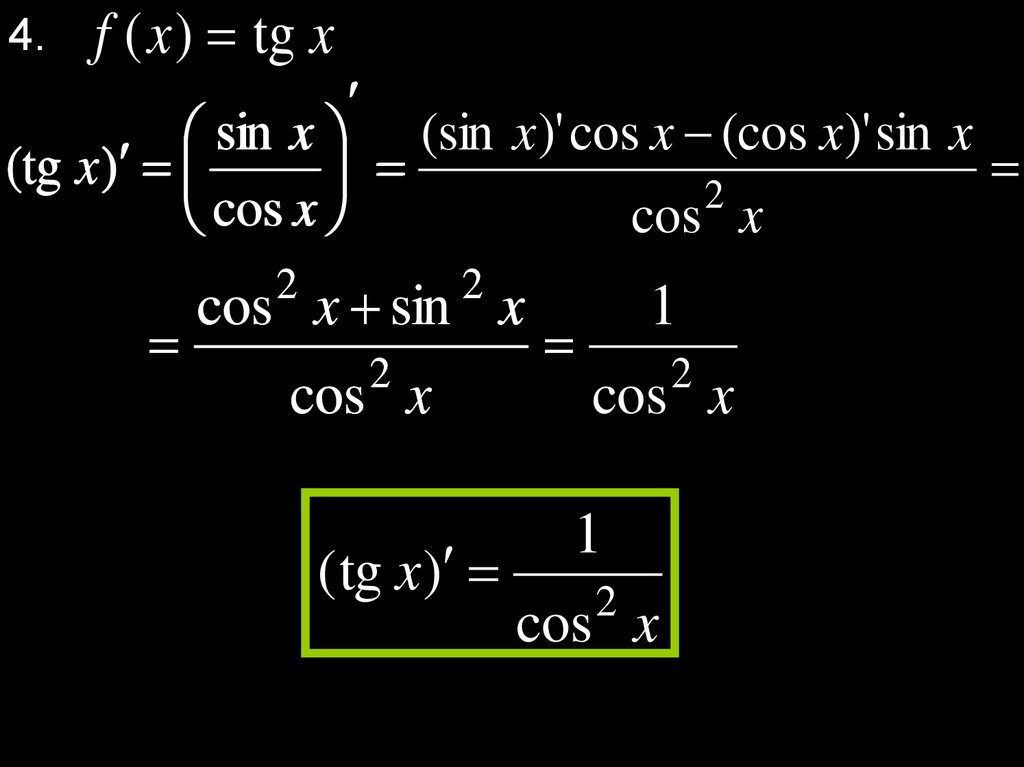

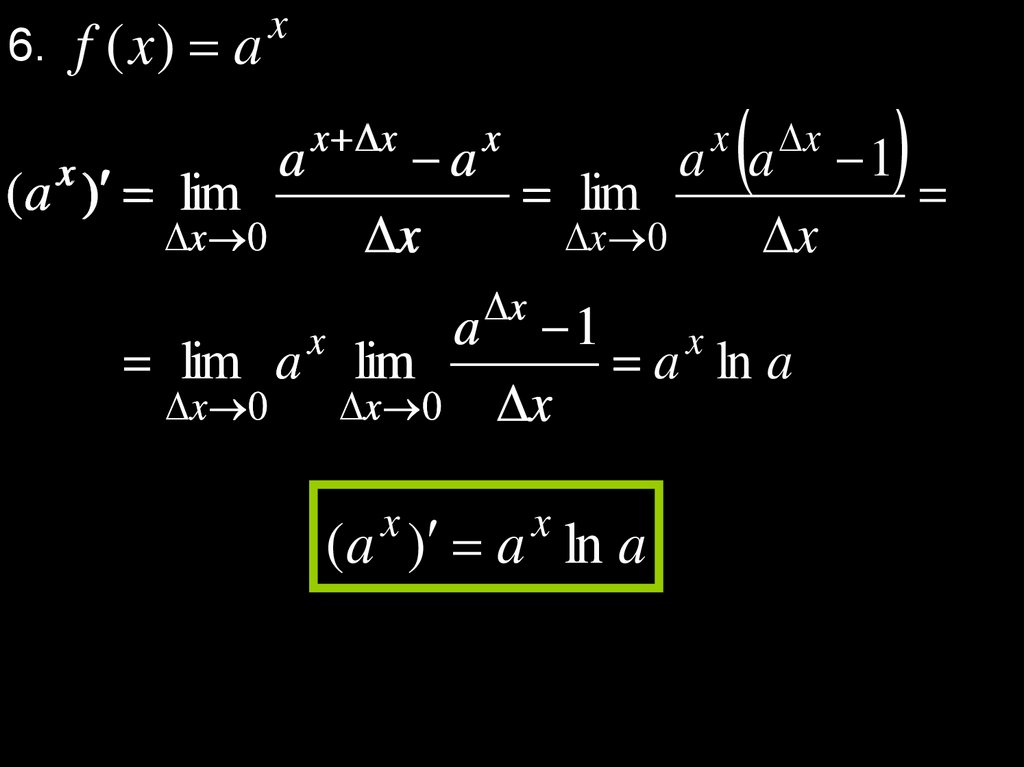











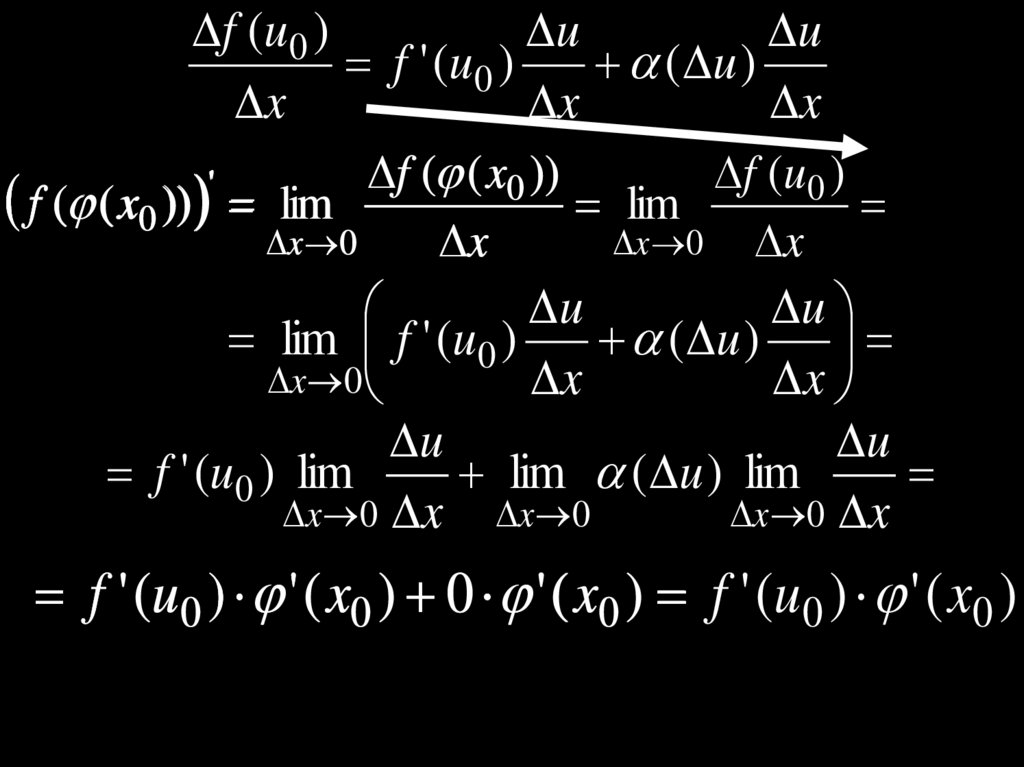
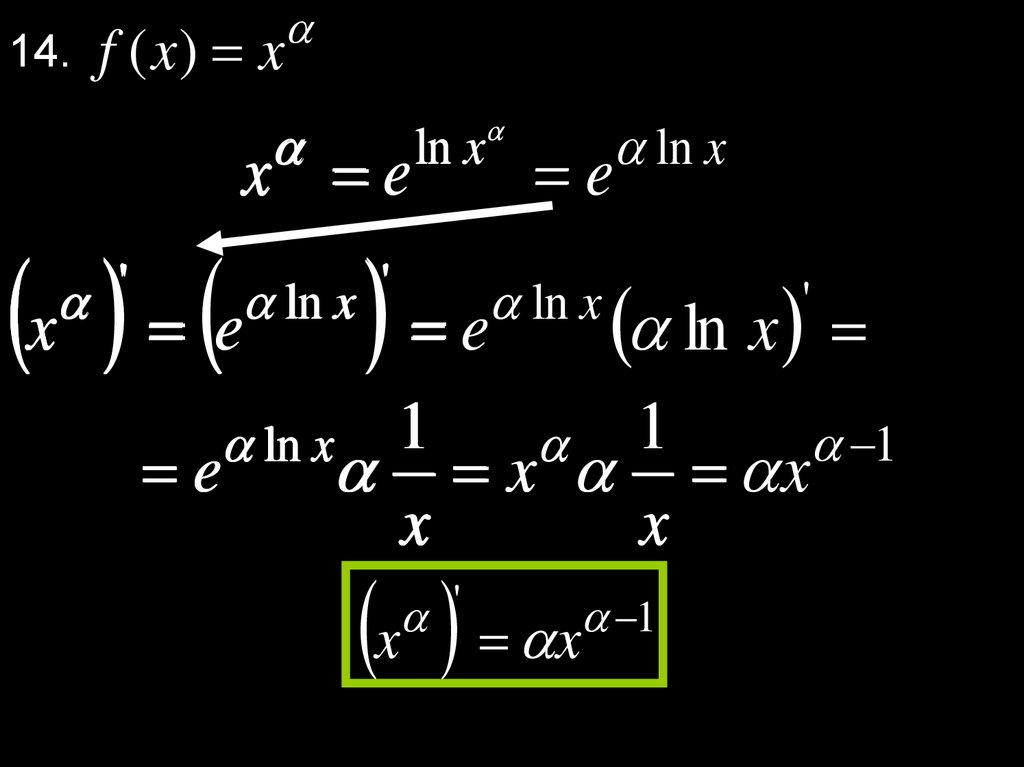
 Математика
Математика








