Похожие презентации:
Геометрические приложения определенного интеграла
1.
Пусть функция y=f(x) – неотрицательная инепрерывна на [a,b]. Тогда площадь под кривой
y=f(x) численно равна определенному интегралу
от этой функции на [a,b].
b
S f ( x ) dx
a
2.
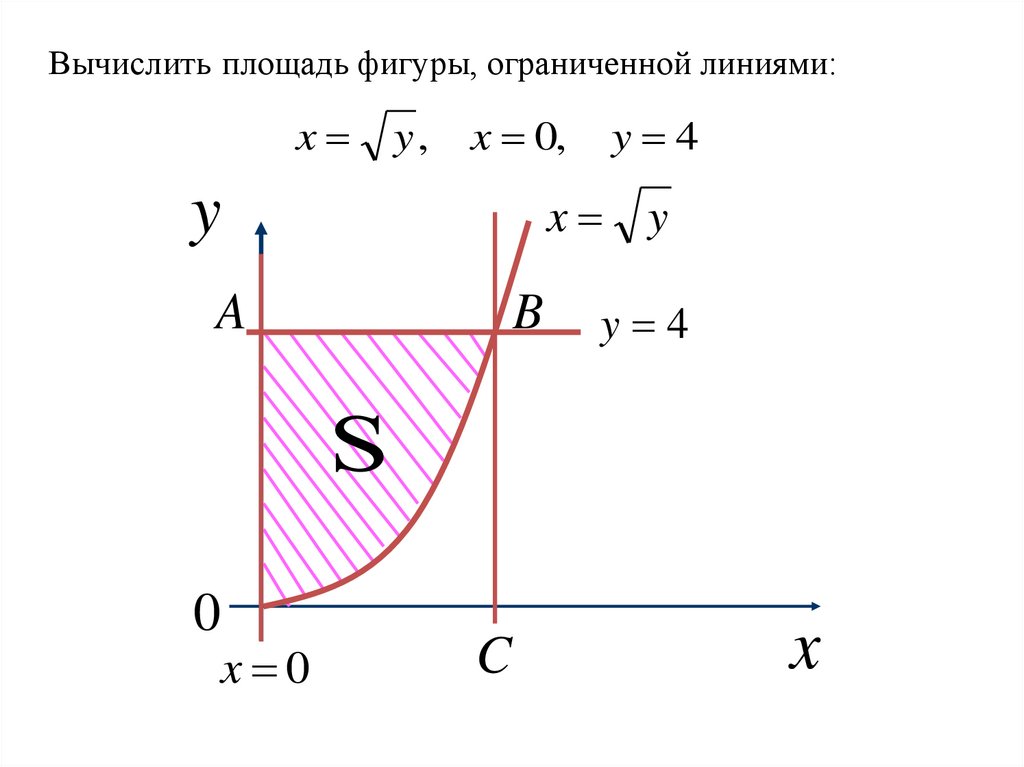
Вычислить площадь фигуры, ограниченной линиями:x
y,
x 0,
y
x y
A
0
x 0
y 4
B
C
y 4
x
3.
S ABC SOABC SOBCНаходим координаты точки В:
y 4
x y
Тогда
y 4
x 2
B(2,4)
2
SOABC 4dx 4 x 0 8
2
0
3 2
2
x
8
S OBC x dx
3 0
3
0
2
8 16
S ABC 8
( кв.единиц )
3
3
4.
Пусть функция y=f(x) – неположительная и непрерывна на[a,b]. Отражая кривую y=f(x) относительно оси абсцисс,
получаем кривую с уравнением y=-f(x).
Функция y=-f(x) – уже неотрицательна на [a,b] и площадь
под этой кривой на [a,b] равна искомой площади.
b
S f ( x)dx
a
5.
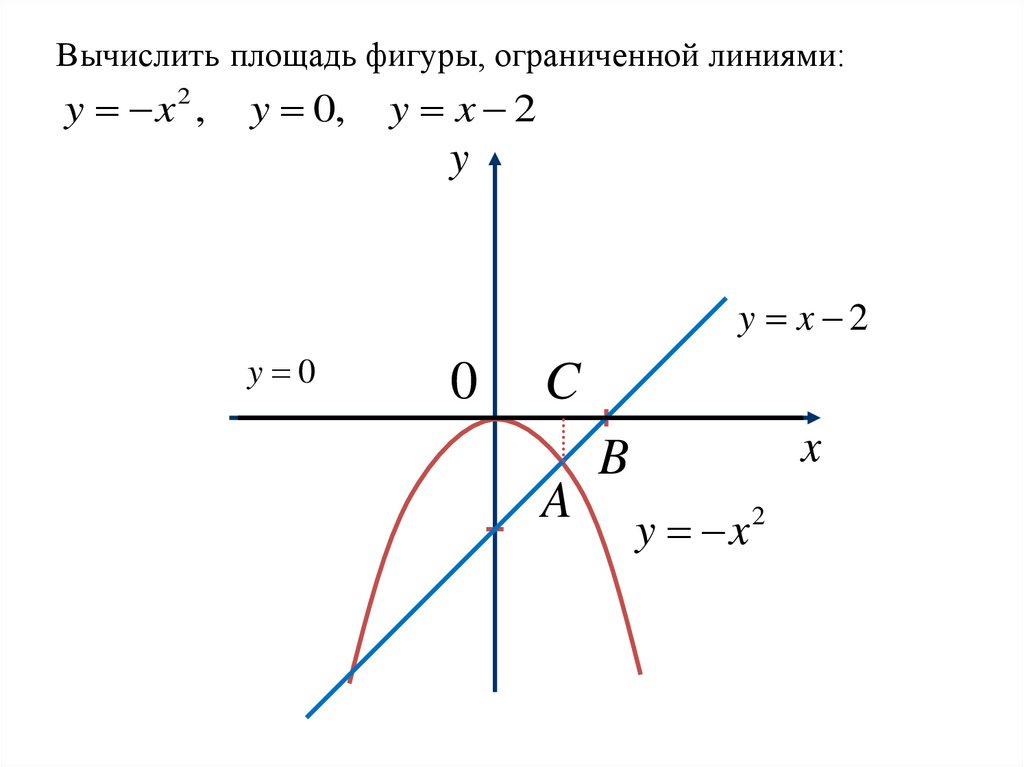
Вычислить площадь фигуры, ограниченной линиями:y x2 ,
y 0,
y x 2
y
y x 2
y 0
0
C
A
x
B
y x2
6.
SОАВ – это площадь над кривой ОАВ на отрезке [0;2]. Ноэта кривая задается не одним уравнением, поэтому
разбиваем площадь ОАВ на части, проецируя точку А на
ось х.
SOBA SOAC SCAB
Находим координаты точек О(0,0), В(2,0), А(1,-1).
3 1
1
x
1
S OAC ( x ) dx
3 0 3
0
2
2
x
1
S ABC ( x 2)dx 2 x
2
1 2
1
2
2
1 1 5
S OBA (кв.единиц )
3 2 6
7.
Пусть функция y=f(x) – непрерывна на [a,b] и исходныйотрезок можно разбить на определенное число интервалов,
таких что на каждом из них y=f(x) знакопостоянна или
равна 0.
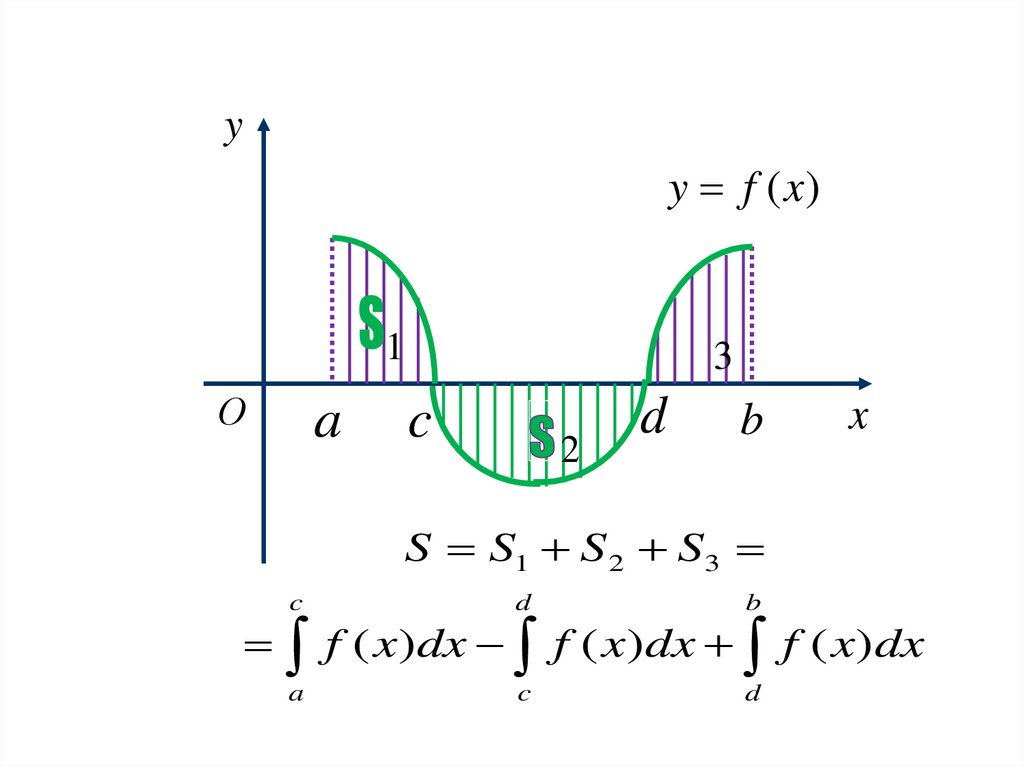
Тогда общая площадь под кривой будет равна сумме
площадей на каждом из отрезков разбиения:
S S1 S 2 ... S n
8.
yy f (x)
1
О
a
3
c
2
d
b
x
S S1 S 2 S3
c
d
b
a
c
d
f ( x)dx f ( x)dx f ( x)dx
9.
Пусть на [a,b] заданы непрерывныефункции y=f1(x) и y=f2(x), такие что
f 2 ( x) f1 ( x)
Тогда площадь фигуры, заключенной между
кривыми y=f1(x) и y=f2(x) на [a,b] находится
по формуле:
b
S f 2 ( x) f1 ( x) dx
a
10.
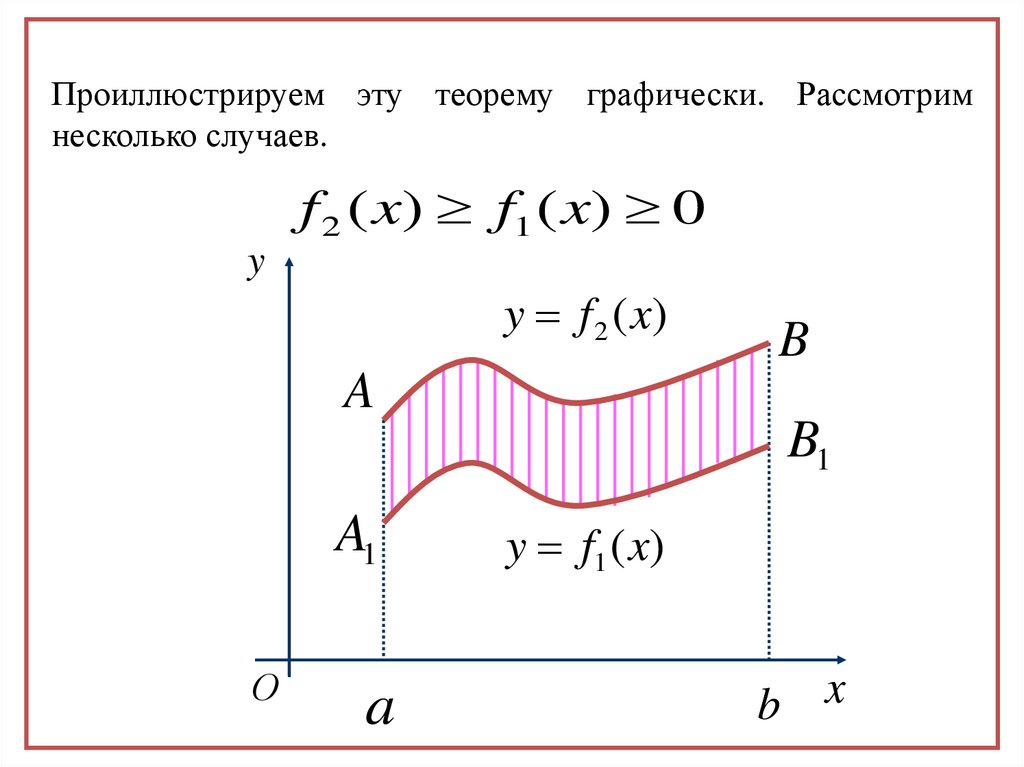
Проиллюстрируем эту теорему графически. Рассмотримнесколько случаев.
f 2 ( x) f1 ( x) 0
y
y f 2 ( x)
B
A
B1
A1
О
a
y f1 ( x)
b x
11.
S S aABb S aA1B1bb
b
a
a
f 2 ( x)dx f1 ( x)dx
b
f 2 ( x) f1 ( x) dx
a
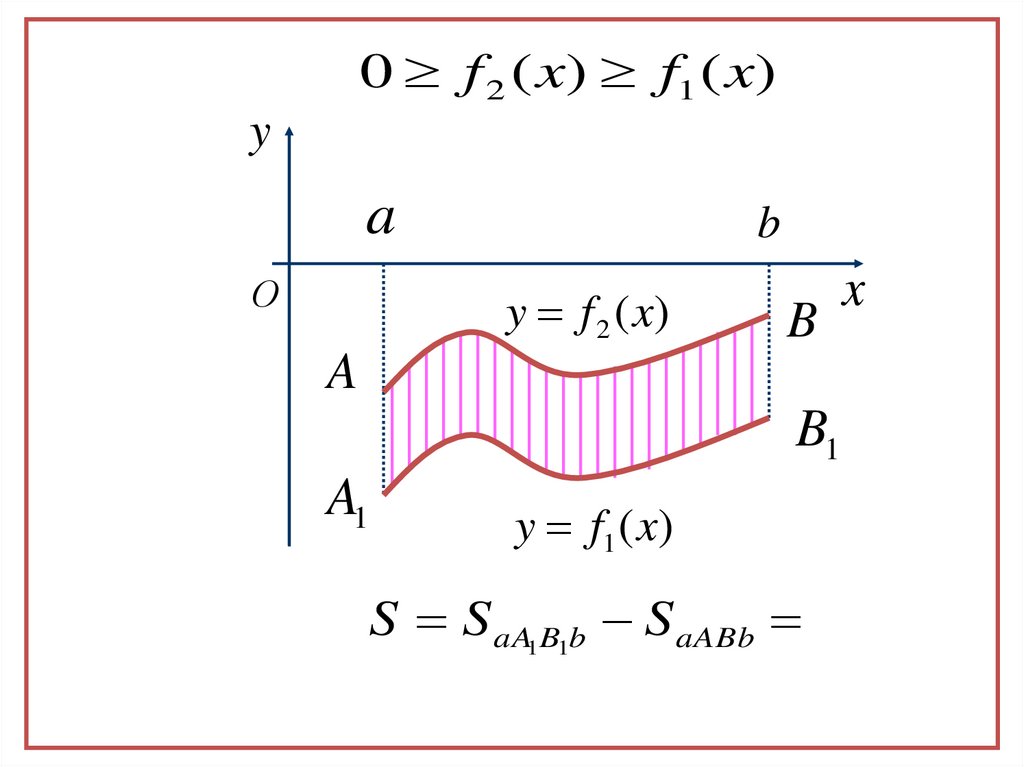
12.
0 f 2 ( x) f1 ( x)y
a
О
b
y f 2 ( x)
B
A
B1
A1
y f1 ( x)
S S aA1B1b S aABb
x
13.
S S aA1B1b S aABbb
f1 ( x) dx f 2 ( x) dx
a
a
b
b
f 2 ( x) f1 ( x) dx
a
14.
yy f 2 ( x)
B
A
О
a
A1
b
B1
y f1 ( x)
f 2 ( x ) f1 ( x )
f 2 ( x) 0
f1 ( x ) 0
x
15.
S S aABb S aA1B1bb
b
a
a
f 2 ( x)dx f1 ( x)dx
b
f 2 ( x) f1 ( x) dx
a
16.
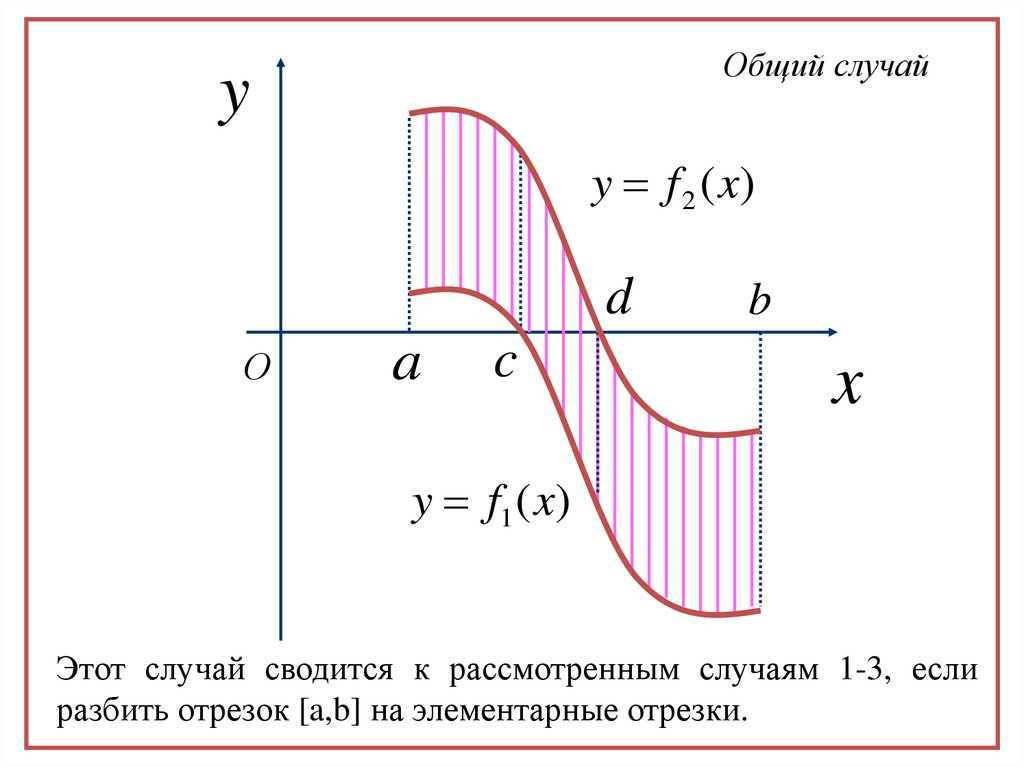
Общий случайy
y f 2 ( x)
d
О
a
c
b
x
y f1 ( x)
Этот случай сводится к рассмотренным случаям 1-3, если
разбить отрезок [a,b] на элементарные отрезки.
17.
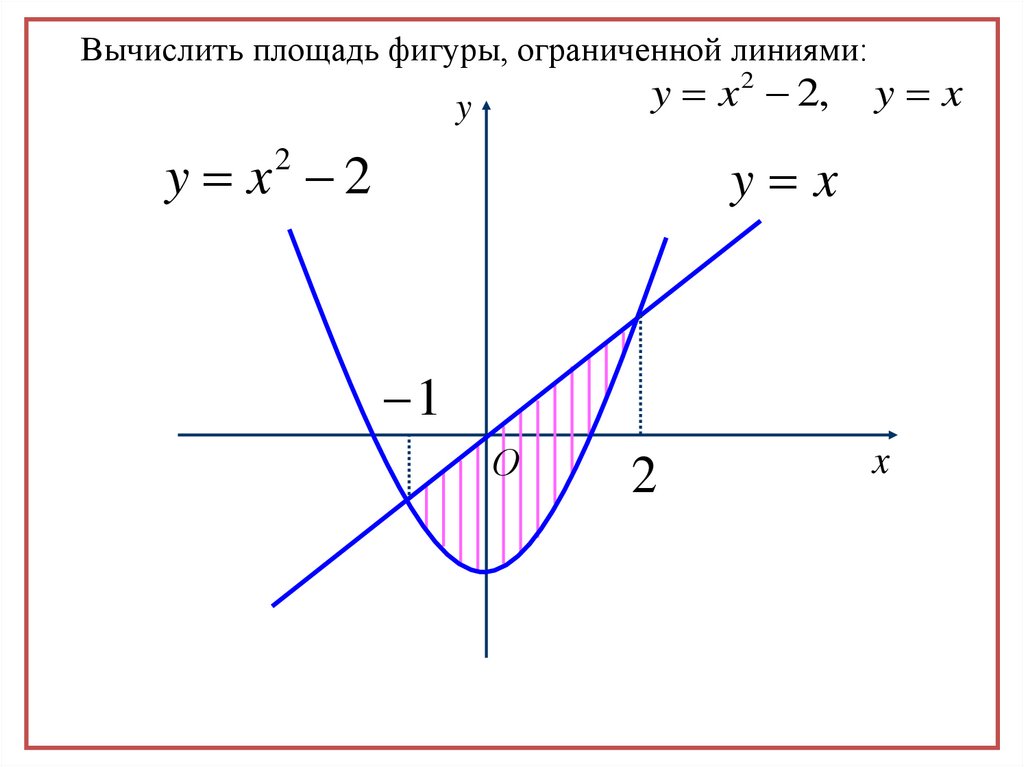
Вычислить площадь фигуры, ограниченной линиями:y x 2 2,
y
y x 2
y x
y x
2
1
О
2
x
18.
Находим координаты точек пересечения линий:y x2 2
y x
x x 2 0 x1 1, x2 2
2
Следовательно, линии пересекаются в точках
( 1, 1),
( 2,2)
f1 ( x) x 2,
2
f 2 ( x) x
2
x x
S ( x x 2)dx 2 x 4,5
2 3
1
1
2
2
2
3
кв.ед.
19.
Пусть функция y=f(x) –знакопостоянная и непрерывнана [a,b]. Найти объем тела Vх, образованного
вращением вокруг оси х криволинейной трапеции,
ограниченной линиями: y=f(x), y=0, x=a, x=b.
Разобьем [a,b] на элементарные отрезки точками
x0 , x1 , x2 ,..., xn
и на каждом из отрезков выберем точку ξi. Найдем значение
функции в этой точке f ( i )
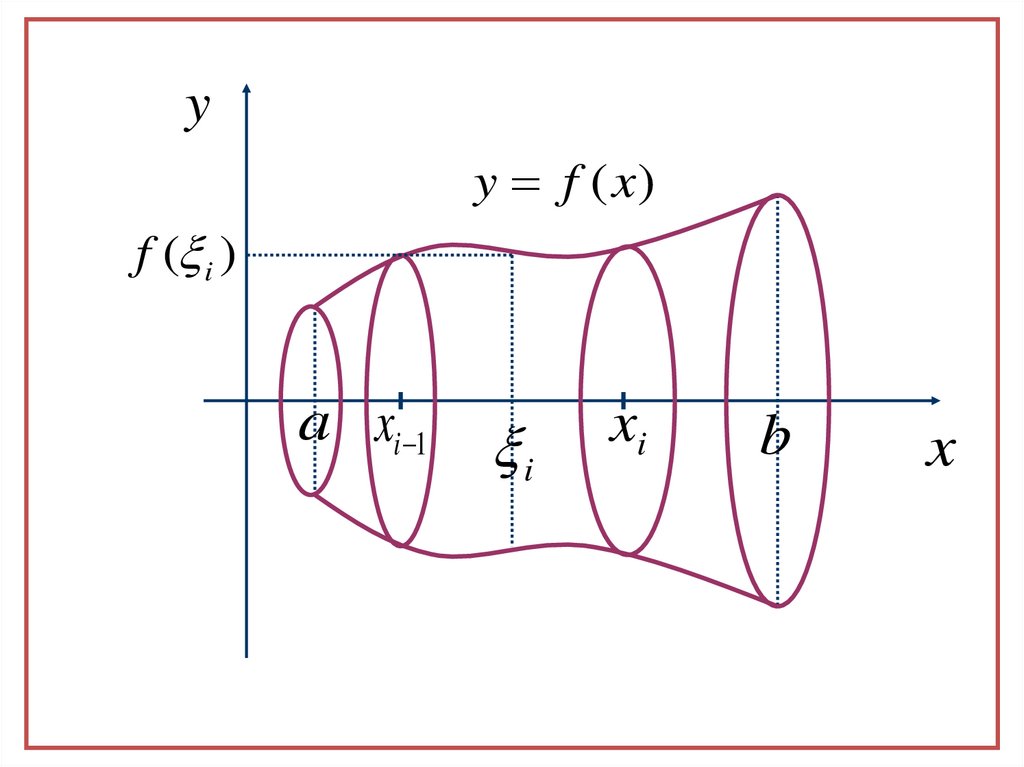
20.
yy f (x)
f ( i )
a xi 1
i
xi
b
x
21.
Тогда некоторое приближение для искомого объема даст суммаn
f ( ) x
2
i 1
i
i
Так как каждое слагаемое это объем цилиндра с высотой
xi xi xi 1
и радиусом основания
f ( i )
Искомый объем будет тем точнее, чем меньше длина отрезков
разбиения
x
i
Поэтому за объем естественно выбрать
22.
Vxn
lim
max xi 0
f ( ) x
2
i 1
i
Правая часть выражения представляет
интегральной суммы функции
f ( x)
2
Поэтому
b
Vx f 2 ( x)dx
a
i
собой
предел
23.
Вычислить объем тела, полученного от вращения вокруг осиабсцисс фигуры, ограниченной линиями:
x
y e ,
y 0,
x 0,
x 1
24.
xy e ,
y 0,
x 0,
x 1
y
y e
x
1
x
25.
1Vx e
0
1
2 x
1 2 x
dx e
2
0
1
1 2 1.36 (куб .единиц )
2 e
26.
Если заменить х на у, то получим формулу для вычисленияобъема тела, полученного от вращения криволинейной
трапеции вокруг оси у.
d
Vy ( y )dy
2
c
27.
Вычислить объем тела, полученного от вращения вокруг осиординат фигуры, ограниченной линиями:
y x ,
2
y
y x
y x
3
y x
1
1
2
x
3
28.
V y V y1 V y 2V y1 ограничен линиями
x 3 y , x 0, y 1
V y 2 ограничен линиями
x y , x 0, y 1
1
2
3
3
V y1 y dy y
5
0
5 1
3
3
5
0
1 2
Vy 2 ydy y
2
2
0
0
1
1
3
1
V y 0.1 (куб .единиц )
5
2






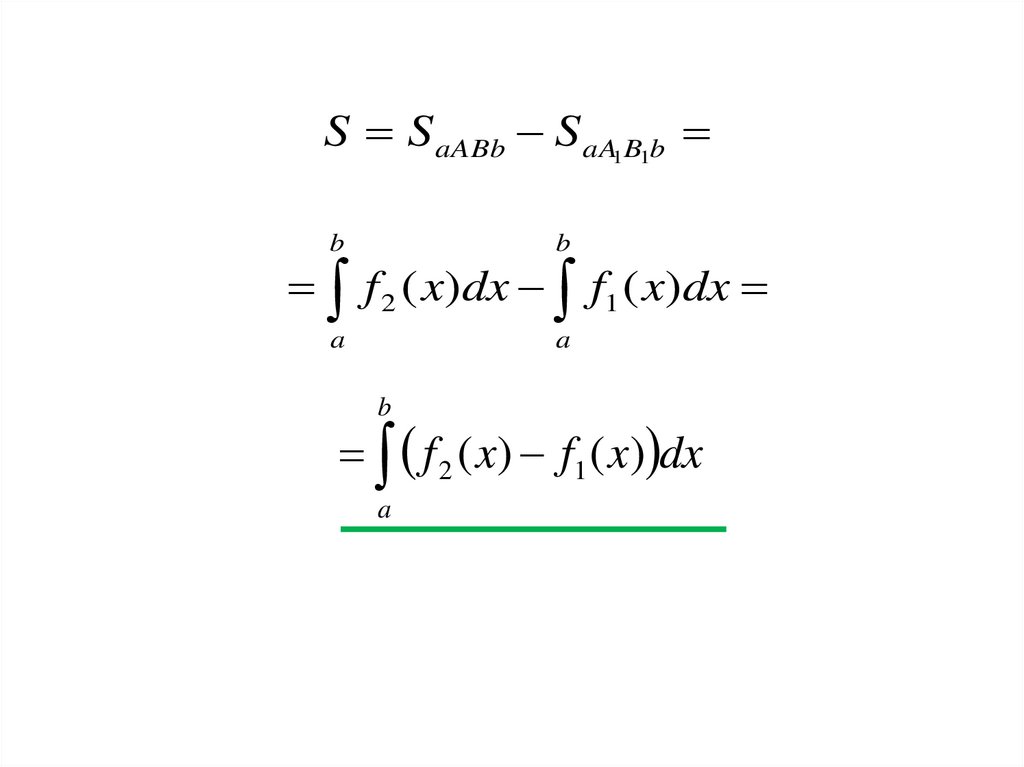
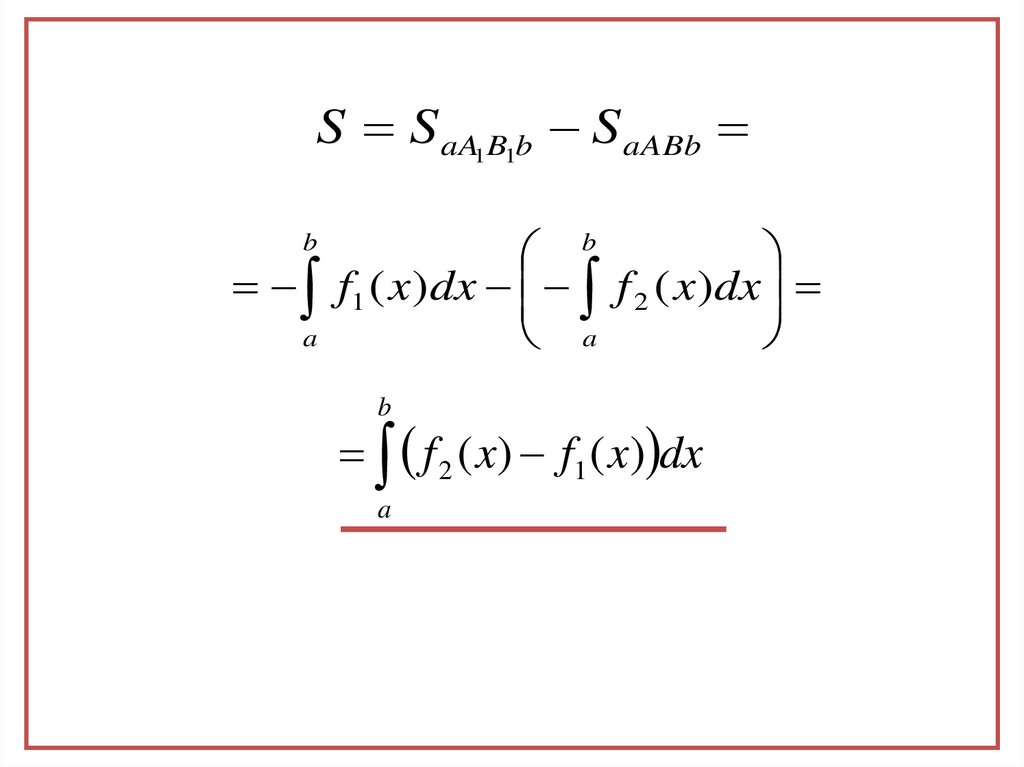

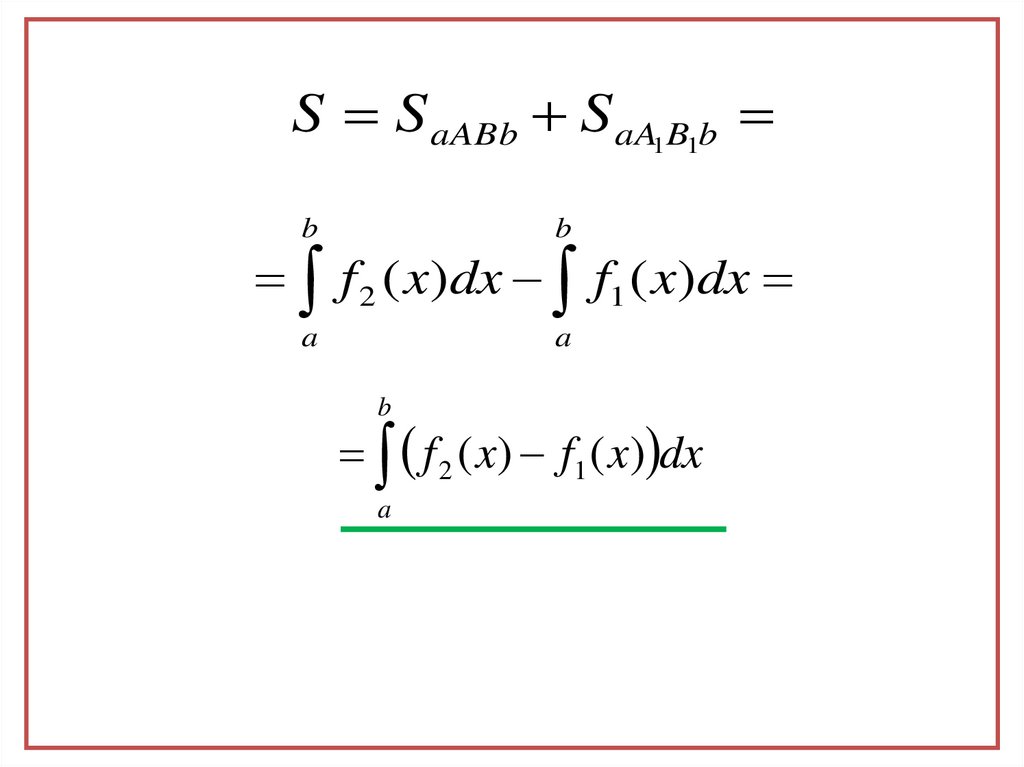






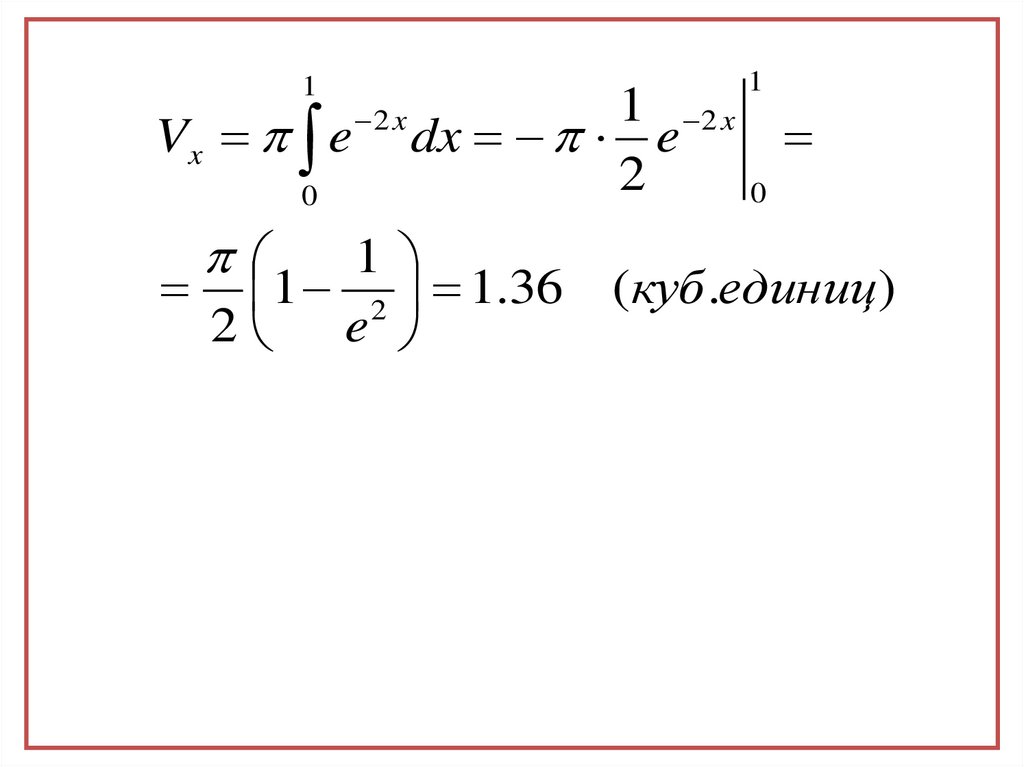




 Математика
Математика








