Похожие презентации:
Приложения Определенного интеграла
1. Приложения Определенного интеграла
Ащеулова Алена Сергеевна,кандидат физико-математических наук
2. Вычисление площадей
23.
yПлощадь
такой
фигуры,
называемой
криволинейной
трапецией,
вычисляют
по
формуле
y f x
x
0
a
b
b
S f x dx
a
3
.
4. Пример 1
yВычислить площадь фигуры,
ограниченной линиями:
x
y,
x 0,
x y
A
B
y 4
y 4
0
x 0
C
x
4
5.
S ABC SOABC SOBCy 4
Находим координаты точки В:
x y
y 4
x 2
B (2; 4)
2
SOABC
2
S OBC
4dx 4 x
0
2
0
3 2
x
x dx
3
0
2
S ABC
0
8
8
3
8 16
8
3
3
5
6. Пример 2
yВычислить площадь фигуры,
ограниченной линиями:
y x ,
2
y x 2
y 0,
y x 2
y 0
0
C
A
B
x
y x
2
6
7.
Находим координаты точек О(0,0), В(2,0), А(1,-1).SOBA SOAC SCAB
3 1
1
S OAC
x
( x )dx
3
0
2
2
x
1
( x 2)dx 2 x
2
1 2
1
2
S ABC
0
1
3
2
SOBA
1 1 5
3 2 6
7
8.
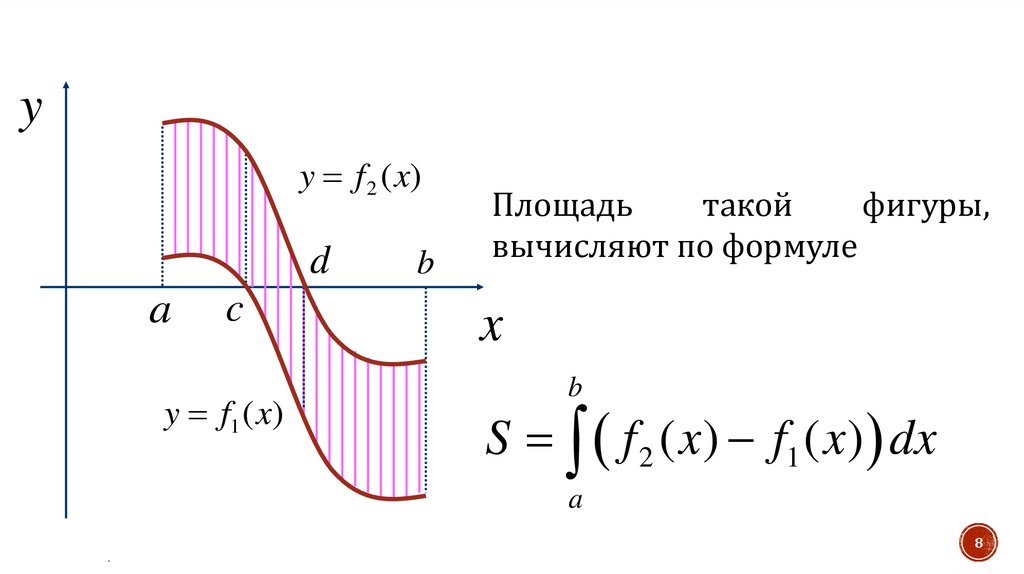
yy f 2 ( x)
d
a
c
y f1 ( x)
b
Площадь
такой
фигуры,
вычисляют по формуле
x
b
S f 2 ( x) f1 ( x) dx
a
8
.
9. Пример 3
yy x 2
y x
2
Вычислить площадь фигуры,
ограниченной линиями:
y x 2,
2
y x
1
2
x
9
10.
Находим координаты точек пересечения линийy x 2
y x
2
x x 2 0 x1 1, x2 2
2
Следовательно, линии пересекаются в точках
f1 ( x) x 2,
2
( 1, 1),
(2,2)
f 2 ( x) x
2
2
3
x x
2
S ( x x 2)dx 2 x 4,5
2 3
1
1
2
10
11. Вычисление объемов тел вращения
1112.
Объем тела, образованного вращением вокруг оси Oxкриволинейной трапеции, ограниченной кривой y f x ,
отрезком оси абсцисс a x b и прямыми x a , x b ,
вычисляется по формуле
b
Vx π
f
x
2
dx
a
Объем тела, образованного вращением вокруг оси Oy
фигуры, ограниченной кривой x g y , отрезком оси
ординат c y d и прямыми y c , y d , вычисляется по
d
формуле
.
Vy
g
y
2
c
dy
12
13. Вращение вокруг оси OX
bVox = y ( x) dx
a
2
b
Vox = [ y2 ( x) y1 ( x)] dx
2
2
a
13
14. Вращение вокруг оси OY
dVoy = x 2 ( y ) dy
c
d
Voy = [ x2 ( y ) x1 ( y )] dy
c
2
2
b
Voy = 2 x y ( x) dx
a
14
15. Пример 4
yВычислить объем тела,
полученного от вращения
вокруг оси абсцисс фигуры,
ограниченной линиями:
x
y e ,
y e x
y 0,
x 0, x 1
1
Vx e
0
2 x
1
1 2 x
1
dx e
1 2 1,36
2
2 e
0
1
x
15
16. Пример 5
yВычислить
объем
тела,
полученного от вращения
вокруг оси ординат фигуры,
ограниченной линиями:
y x ,
2
y x
y x3
y x
1
2
3
1
x
16
17.
V y V y1 V y 2V y1
ограничен линиями
x 3 y , x 0, y 1
Vy 2
ограничен линиями
x y , x 0, y 1
1
2
3
5 1
3
3
3
Vy1 y dy y
5
5
0
0
1
1
1 2
Vy 2 ydy y
2
2
0
0
3
1
Vy 0,1
5
2
17
18. Задание 1
Вычислите площади фигуры18
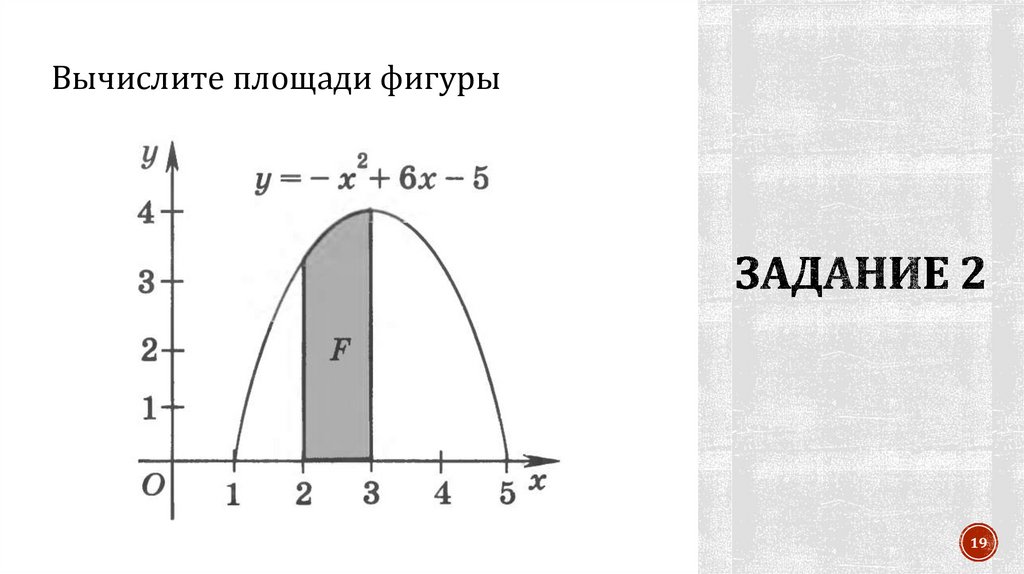
19. Задание 2
Вычислите площади фигуры19
20. Задание 3 Задание 4
3. Вычислите площадиограниченной линиями
y x 1
фигуры
y x 2x 3
2
2
4.
Вычислите
объем
фигуры
полученной вращением вокруг оси
криволинейных
трапеций,
ограниченных линиями
y x
2
y x
20


















 Математика
Математика








