Похожие презентации:
Определенный интеграл. Приложения определенного интеграла
1.
Математика ППИ.ЛЕКЦИЯ № 14.
Определенный интеграл.
Приложения определенного
интеграла.
2. ВОПРОСЫ ЛЕКЦИИ
5. Вычисление объемов тел и площадейповерхностей тел вращения.
3. ЛИТЕРАТУРА
[1] Н.С. Пискунов. Дифференциальное и интегральноеисчисления. Т 1. Москва: Интеграл-Пресс, 2004. с.
340-375;
[3] Б.П. Демидович, В.А. Кудрявцев. Краткий курс
высшей математики. Москва: Издательство АСТ,
2004.. с. 229-250;
[14] Л.К. Потеряева, Г.А. Таратута. Курс высшей
математики IV. Челябинск: Челябинский военный
авиационный краснознамённый институт штурманов,
2002 г.с. 80-94.
4. Вычисление объемов тел вращения
Теорема. Пусть функция f(x) непрерывна инеотрицательна на отрезке [a;b]. Тогда тело,
образованное
вращением
вокруг
оси
Ox
криволинейной трапеции, ограниченной графиком
функции y=f(x), имеет объем V, который может быть
найден по формуле: b
V y 2 dx
a
5.
Доказательство. Разобьем отрезок [a;b] точкамиa=x0,x1,…,x i-1,xi,…,xn=b на n частей;
причем xi- x i-1 = Δxi , обозначим λ=max Δxi .
6.
На каждом из частичных отрезков [xi-1 ; xi]выберем произвольно точку сi ; а также на каждом
частичном отрезке [xi-1 ; xi] построим прямоугольник,
который при вращении вокруг оси Ox опишет цилиндр
с высотой Δx i и радиусом основания f(ci), объем
которого
ΔVi= π∙f 2(сi)∙Δxi.
7.
Найдем объем соответствующего ступенчатого тела,составив интегральную сумму
n 2
f (ci ) xi
i 1
Для непрерывной функции f(x) предел интегральной
суммы существует при λ→0 (n→∞) и равен объему
рассматриваемого тела вращения
n
b
V lim f 2 (ci ) xi f 2 ( x)dx
0 i 1
a
n
8.
Таким образом,b
b
V f 2 ( x)dx y 2 dx
a
a
что и требовалось доказать
9.
Пример.Найдите объем тела, образованного
вращением вокруг оси Ox фигуры, ограниченной
линиями y=ex, x=1 и осями координат .
Решение.
10.
Фигура, ограниченная данными линиями,является криволинейной трапецией, поэтому
получим
1
1
V (e ) dx e dx
x
0
2
2x
0
1
e d ( 2 x)
20
2x
2
1
e
2x
0
2
(e 2 1) 10,1
11.
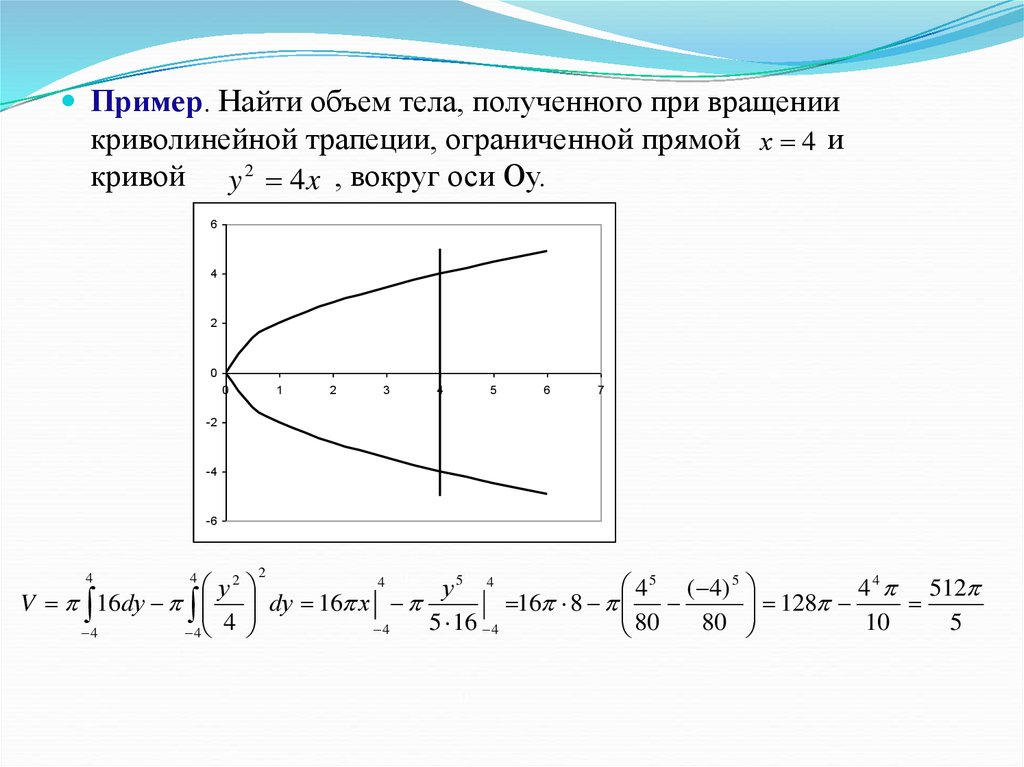
Пример. Найти объем тела, полученного при вращениикриволинейной трапеции, ограниченной прямой х 4 и
кривой y 2 4 x , вокруг оси Оу.
6
4
2
0
0
1
2
3
4
5
6
7
-2
-4
-6
у2
V 16dу
4
4
4
4
4
2
4
4 5 ( 4) 5
у5 4
4 4 512
dу 16 х
128
16 8
5
16
80
80
10
5
4
4
12. Площадь поверхности вращения
Пусть дана поверхность, образованная вращениемдуги линии y=f(x), a≤x≤b, относительно оси Ox.
Предположим, что на отрезке [a;b] функция y=f(x) и
её производная f´(x) непрерывны и, кроме того,
f(x) ≥0. Тогда площадь поверхности вращения
можно вычислить по формуле
b
P 2 f ( x) 1 ( f ( x)) 2 dx
a
13.
Пример. Найти площадь поверхности шарарадиуса R.
Решение. Можно считать, что поверхность шара
образована вращением полуокружности y R 2 x,2
-R≤x≤R, вокруг оси Ox. По формуле находим
x
S 2 R 2 x 2 1
2
2
R
R x
R
2
R
2 x 2 x 2 dx 2 Rx R 4 R 2
dx 2
R
R
R
14.
Площадь поверхности вращения кривой, заданнойпараметрическими уравнениями
x x(t ),
y y (t ), t t t
1
2
можно вычислить по формуле
t2
Р 2 y(t ) ( x (t )) 2 ( y (t )) 2 dt
t1
15.
Площадь поверхности вращения кривой, заданной вполярной системе координат уравнением
( ) ,
можно вычислить по формуле
Р 2 sin 2 ( ) ( ( )) 2 d
16.
Контрольная работа № 3Найти интегралы
4
5
1)
4
x3
x
,
.
,
,
3)
5)
dx
,
,
2 xdx
3
4 ln x
4) 3 dx
x
5 4 x2
3x 4
8x 4x2 3
dx
,
3
.
6 xdx
2) 2
3 x 1
cos x
6)
dx
2
2 sin x
x
dx
x 2















 Математика
Математика








