Похожие презентации:
Алгебра и начала анализа
1. Алгебра и начала анализа
2.
3.
4. Интеграл. Площадь криволинейной трапеции
5.
Цели и задачи урока:• Обобщить и систематизировать теоретический
материал по теме.
• Усовершенствовать
навыки
вычисления
первообразных для функций.
• Усовершенствовать
навыки
вычисления
определенного интеграла по формуле Ньютона–
Лейбница.
• Систематизировать, расширить и углубить
знания по данной теме.
• Способствовать развитию умения сравнивать,
обобщать, классифицировать, анализировать,
делать выводы.
• Побуждать учащихся само- и взаимоконтролю,
воспитывать
познавательную
активность,
самостоятельность, упорство в достижении цели.
6. Интеграл. Площадь криволинейной трапеции
7.
Три правила нахожденияпервообразных
1º Если F(x) есть первообразная для f(x), а G(x) –
первообразная для g(x), то F(x) + G(x) есть
первообразная для f(x) + g(x).
2º Если F(x) есть первообразная для f(x), а k –
постоянная, то функция kF(x) есть первообразная
для kf.
3º Если F(x) есть первообразная для f(x), а k и b –
1
постоянные, причем k ≠ 0, то функция
F(kx + b)
k
есть первообразная для f(kx + b).
8. Задание № 1.
Назовите номера техфункций,
первообразная которых
находится только по
одному из правил:
а) по правилу суммы;
б) по правилу
умножения на
постоянный множитель;
в) по правилу сложной
функции.
И почему? Поясните
ответ.
1. y x x ;
2. y 2 cos x;
3
3. y 8 5 x 10 x ;
2
4. y 4 3 x ;
9
5. y 4sin 3 x;
6. y 4 x.
9. Задание №2. Установить соответствие. Найти такой общий вид первообразной, которая соответствует заданной функции.
x1. F x cos x C
2
x2 x4
2. F ( x) C
3
2 4
1. f x x x
5 x 2 10 x3
3.F ( x) 8 x
C
2
3
2. f x 2 cos x
4. F ( x) 2sin x C
3. f x 8 5 x 10 x
4. f x 4 3 x
9
2
10 x 2
5.F ( x) 8 x sin x
C
3
1
10
6. F ( x) 4 3x C
30
1
10
7. F ( x) 4 3x C
3
10. Задание № 3
Найти ошибку в вычислениях первообразной иинтеграла
а ) f x 7 x 4
7 2
F x x 4 C.
2
2
б ) f x 3x 7
3x 7 dx x C. +7х
2
3
11. Задание № 3 (продолжение)
3в ) f x 2 2sin 3x
x
3
F x 2cos3x C.
x
x
г ) f x 3cos 2sin 4 x
4
x
x 1
3cos 4 2sin 4 x dx 3sin 4 2 cos4 x C.
12. Лейбниц Готфрид Вильгельм (1646-1716)
Немного историиЛейбниц Готфрид Вильгельм
(1646-1716)
« Общее искусство знаков
представляет чудесное
пособие, так как оно
разгружает воображение…
Следует заботиться о том,
чтобы обозначения были
удобны для открытий.
Обозначения коротко
выражают и отображают
сущность вещей. Тогда
поразительным образом
сокращается работа
мысли.»
Лейбниц
13.
Исаак Ньютон(1643-1727)
14.
• «Интеграл» придумал Я.Бернулли(1690)
• «восстанавливать» от латинского
integro
«целый» от латинского
integer
15.
bS f ( x)dx F х F (b) F (a)
b
a
a
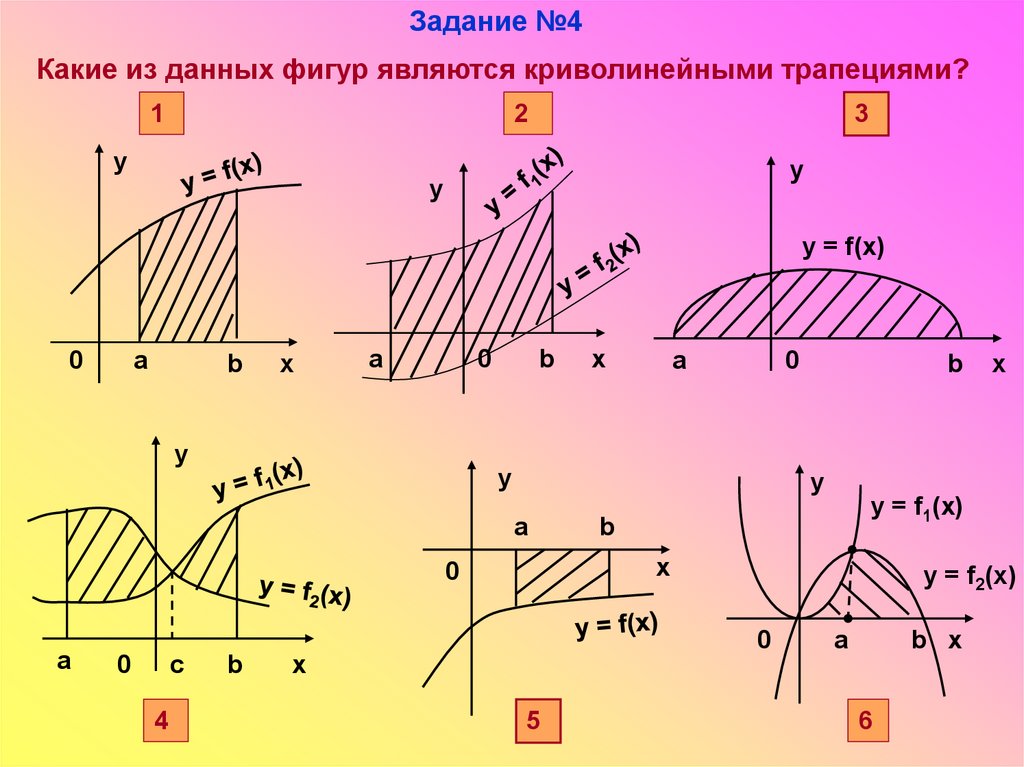
16. Какие из данных фигур являются криволинейными трапециями?
Задание №4Какие из данных фигур являются криволинейными трапециями?
1
2
3
у
y
y
y = f(x)
0
a
b
х
a
0
b
x
a
0
b
x
y
y
y
a
b
x
0
a
y = f1(x)
y = f2(x)
0
0
c
4
b
a
b x
x
5
6
17. Определенный интеграл
bb
f
(
x
)
dx
F
(
x
)
F
(
b
)
F
(
a
)
a
a
– формула Ньютона-Лейбница.
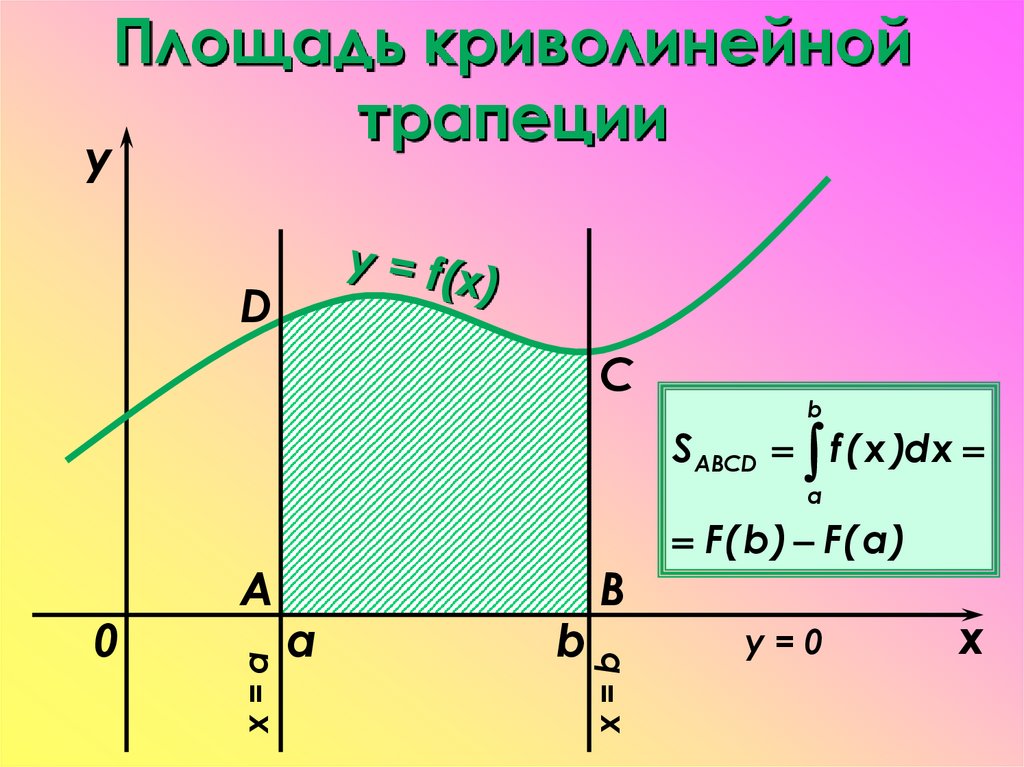
Геометрический смысл определенного интеграла
заключается в том, что определенный интеграл
равен
площади
криволинейной
трапеции,
образованной линиями:
сверху ограниченной кривой у = f(x),
и прямыми у = 0; х = а; х = b.
18. Площадь криволинейной трапеции
yПлощадь криволинейной
трапеции
D
C
b
S ABCD f ( x )dx
a
a
b
B
x=b
x=a
0
A
F( b ) F( a )
y=0
x
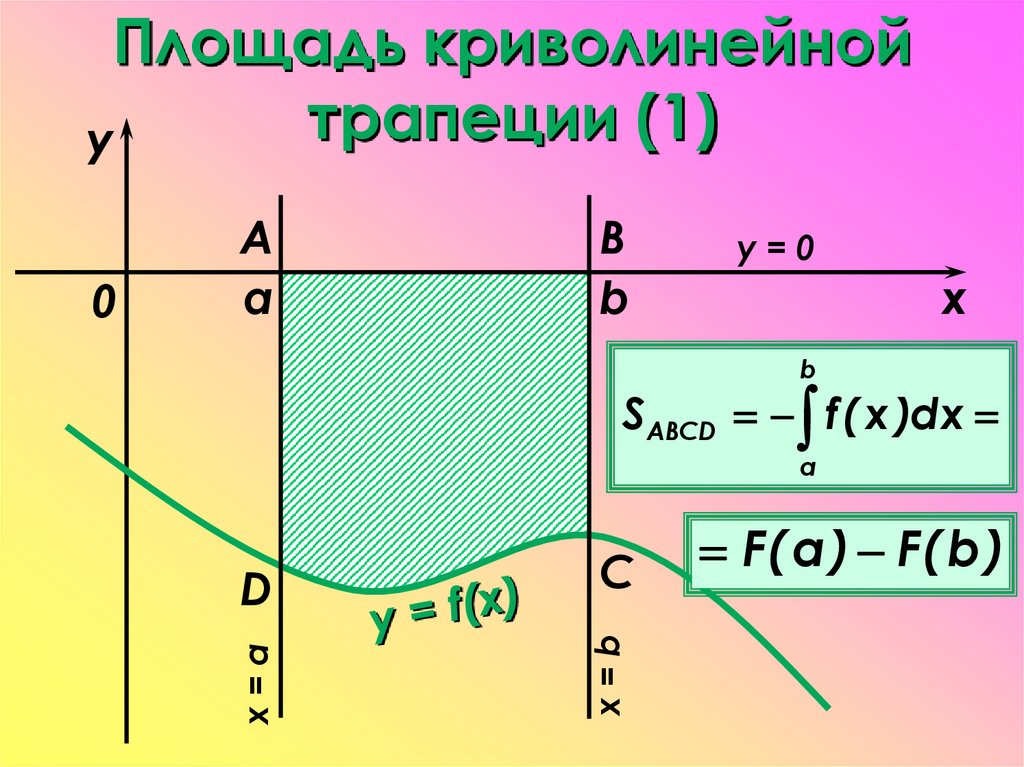
19. Площадь криволинейной трапеции (1)
yB
b
y=0
x
b
S ABCD f ( x )dx
D
C
x=b
a
x=a
0
A
a
F( a ) F( b )
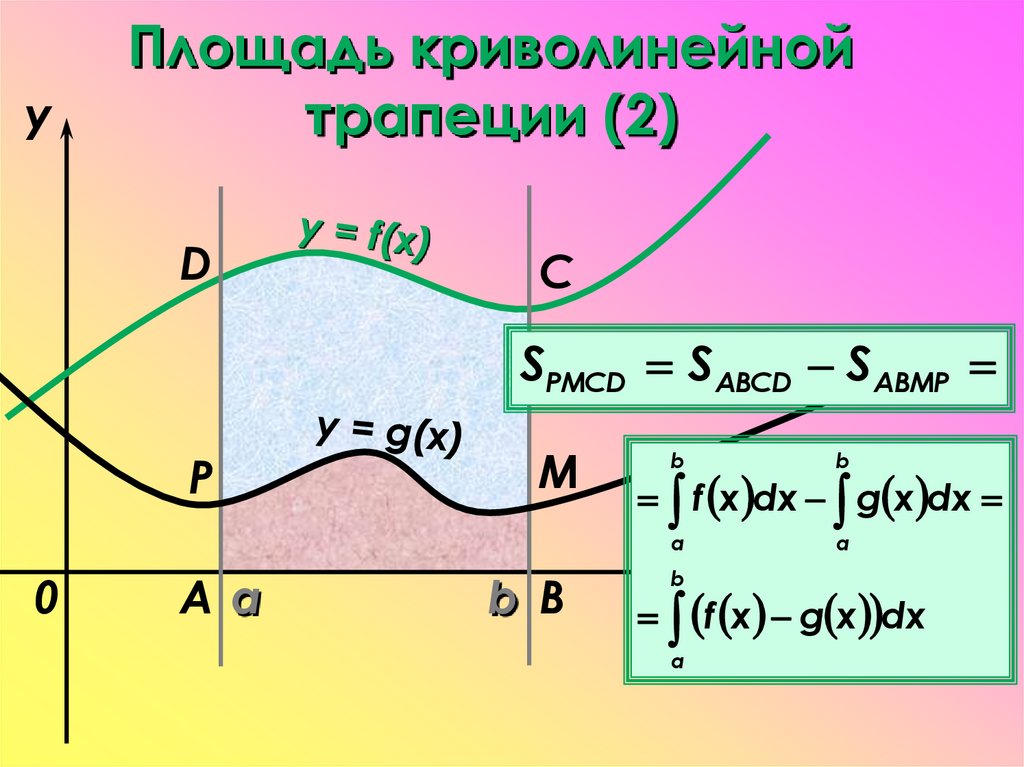
20.
yПлощадь криволинейной
трапеции (2)
D
C
SPMCD SABCD SABMP
P
0
Aa
M
b B
b
b
a
a
f x dx g x dx
b
x
f x g x dx
a
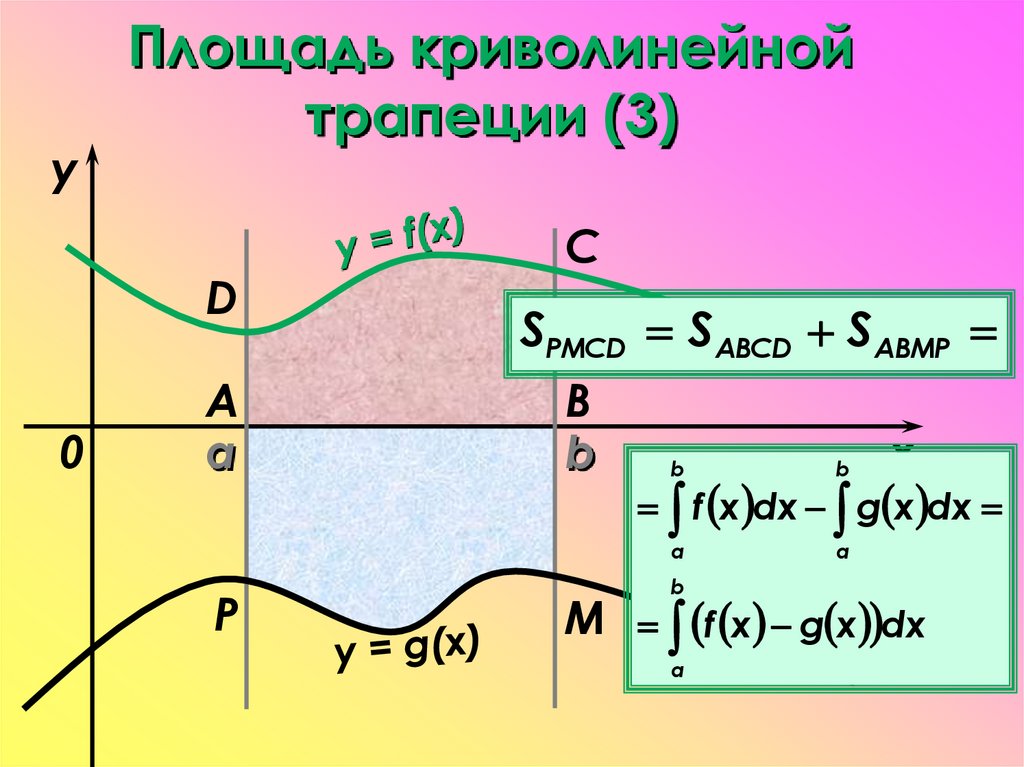
21.
yПлощадь криволинейной
трапеции (3)
D
0
A
a
P
C
SPMCD SABCD SABMP
B
b
b
b
a
a
x
f x dx g x dx
b
M f x g x dx
a
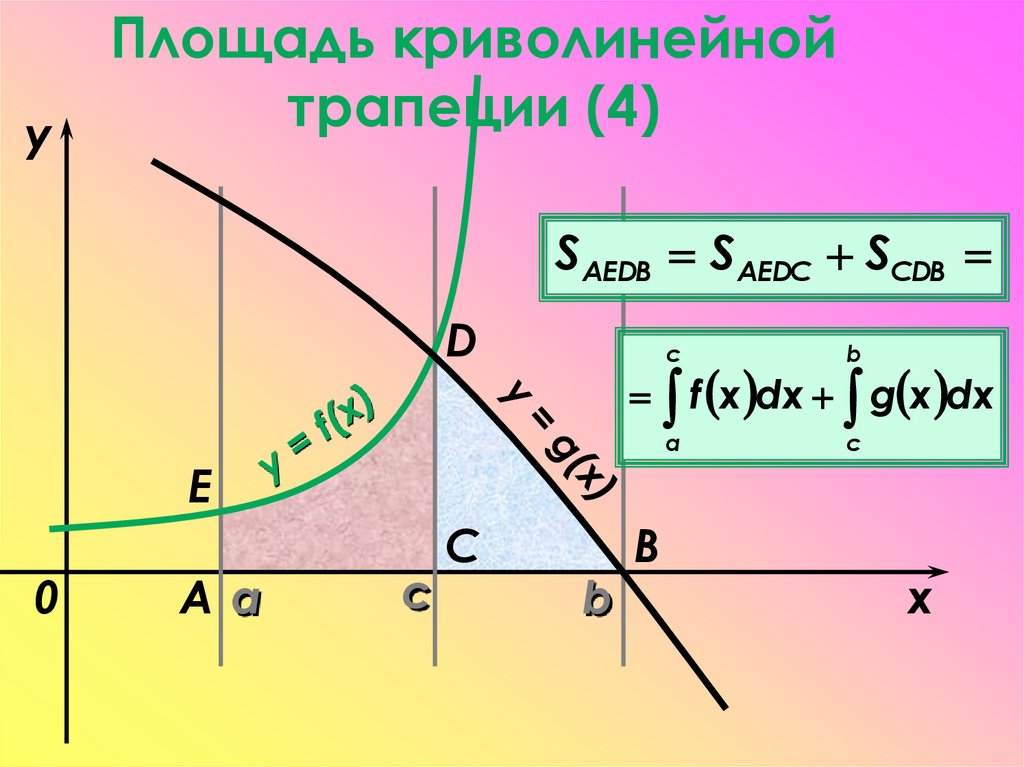
22.
yПлощадь криволинейной
трапеции (4)
SАЕDВ SAEDC SСDB
D
с
b
a
с
f x dx g x dx
Е
0
Aa
с
C
b
B
x
23. Пример 5:
Вычислить площадь фигуры,ограниченной линиями y = x2, y = x + 2.
y
SВОС SABCD SABOCD
C
2
2
1
1
x 2 dx x 2 dx
B
A
-1
2
2
2
x
x
х 2 х 2 dx 2x
3 1
2
1
O
D
2
2
3
8 1
1
1
2 4 2 5 4,5
3 2
3
2
x
24.
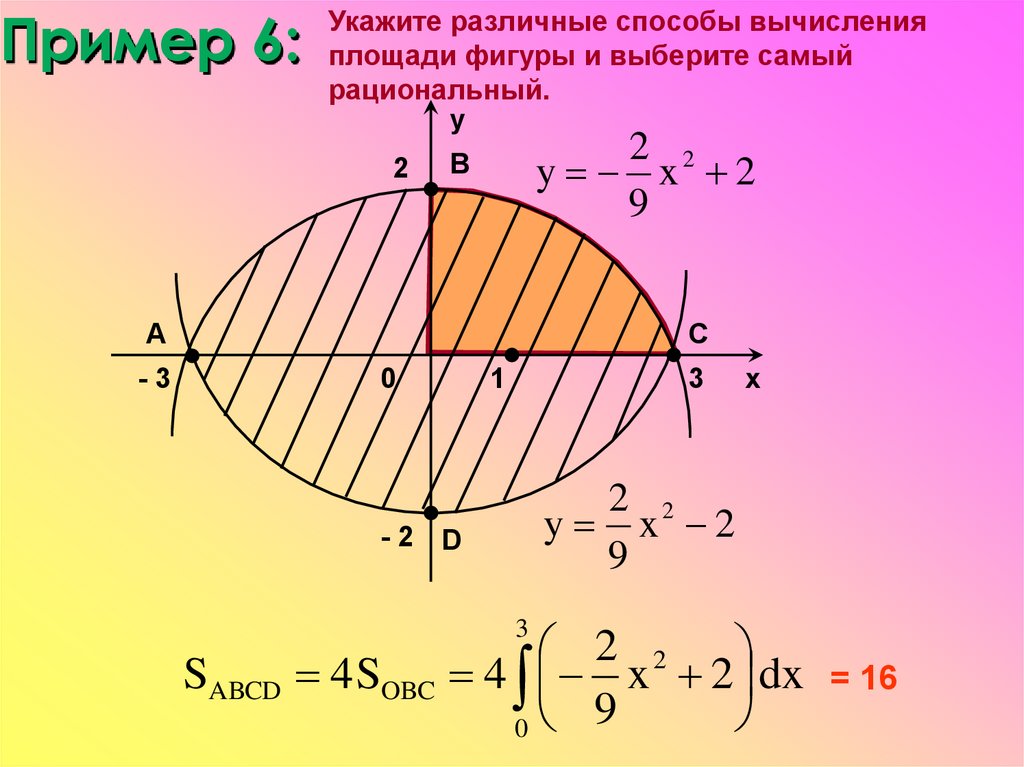
Пример 6:Укажите различные способы вычисления
площади фигуры и выберите самый
рациональный.
y
2
2 2
y x 2
9
B
A
-3
C
0
1
3
x
2 2
y x 2
9
-2 D
2 2
SABCD 4 SOBC 4 x 2 dx = 16
9
0
3
25.
26.
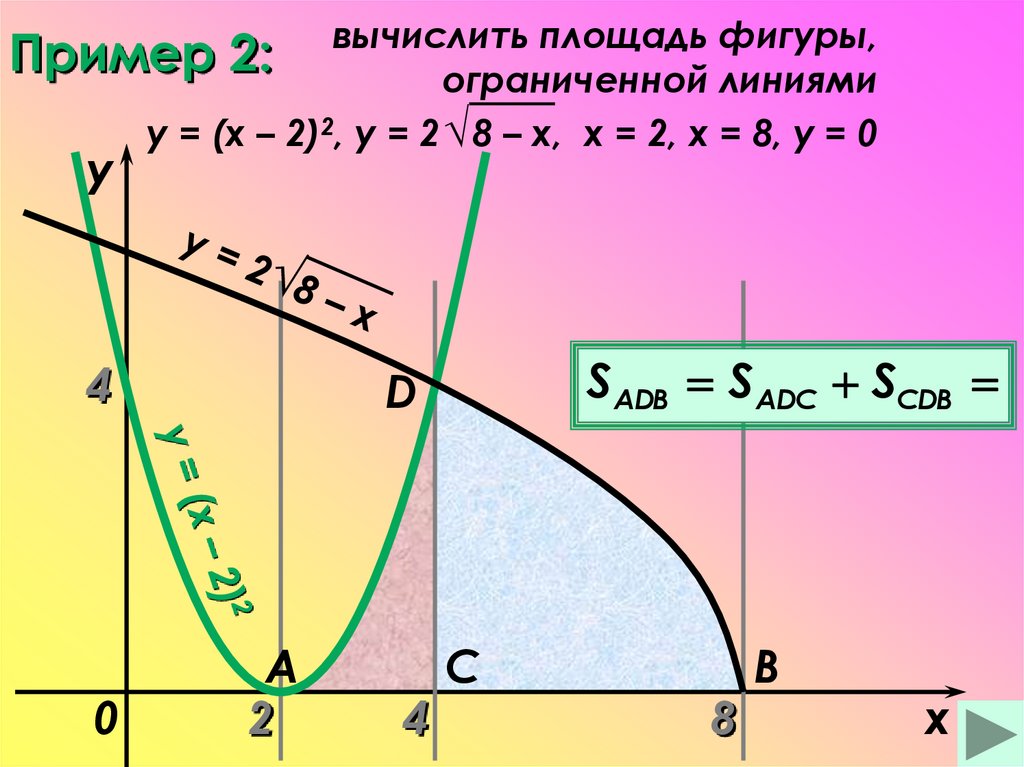
вычислить площадь фигуры,Пример 2:
ограниченной линиями
y = (x – 2)2, y = 2 √ 8 – x, х = 2, х = 8, у = 0
y
4
0
SАDВ SADС SСDB
D
A
2
4
C
8
B
x
27.
вычислить площадь фигуры,Пример 2:
ограниченной линиями
y = (x – 2)2, y = 2 √ 8 – x, х = 2, х = 8, у = 0
3 4
x 2
x - 2 dx 2 8 - хdx
4
2
2
8
4
3
8
4 8 x 8 x
3
2
4
4 2 3 2 2 3 4 8 8 8 8 4 8 4 8 4
3
3
3
3
8 32 40
1
13
3 3
3
3
28. Домашнее задание:
1. Вычислить площадь фигуры, расположенноймежду линиями
у = х² – 2х, у = 4 – х².
2. §27, №1017 в)
3. Вычислительный эксперимент
Спасибо за урок!
Дальнейших успехов!
29.
Определенный интеграл,Ты мне ночами начал сниться,
Когда тебя впервые брал,
Я ощутил твои границы.
И ограниченность твоя
Мне придавала больше силы.
С тобой бороться должен я,
Но должен победить красиво!
Замен и подстановок ряд
Привел к решению задачи.
Ты побежден! Ты мною взят!
Да и могло ли быть иначе…
Как ты поверженный лежал
Числом обычным на странице.
Определенный интеграл,
Кому теперь ты будешь сниться?
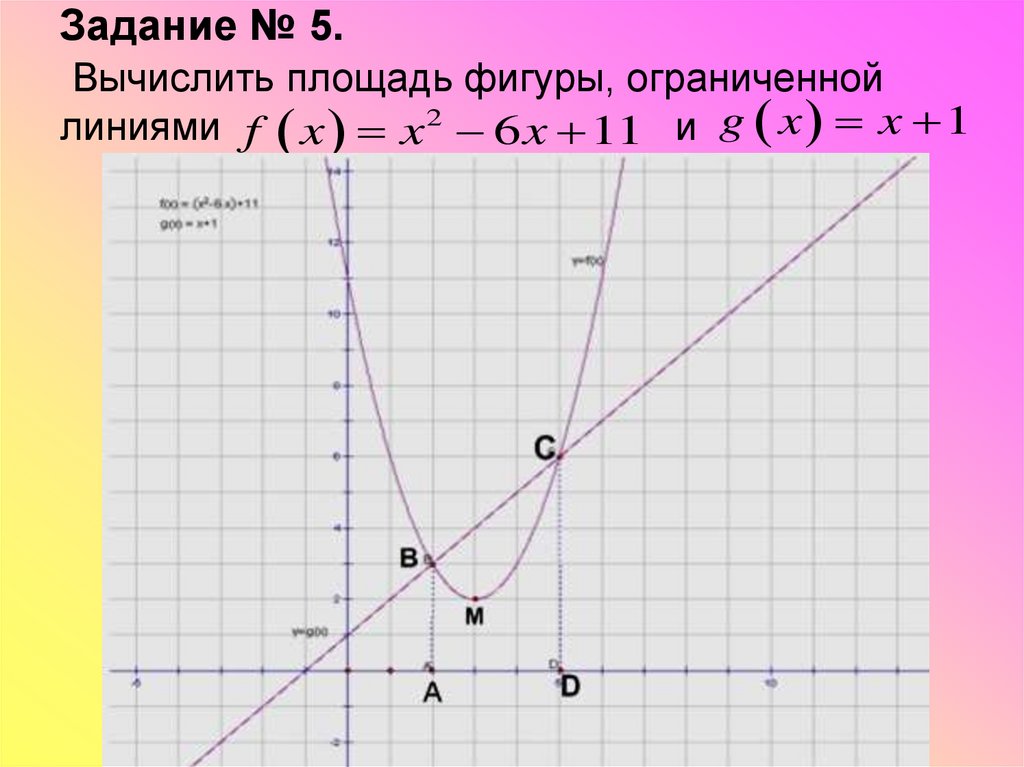
30. Задание № 5. Вычислить площадь фигуры, ограниченной линиями и
Задание № 5.Вычислить площадь фигуры, ограниченной
линиями f x x 2 6 x 11 и g x x 1










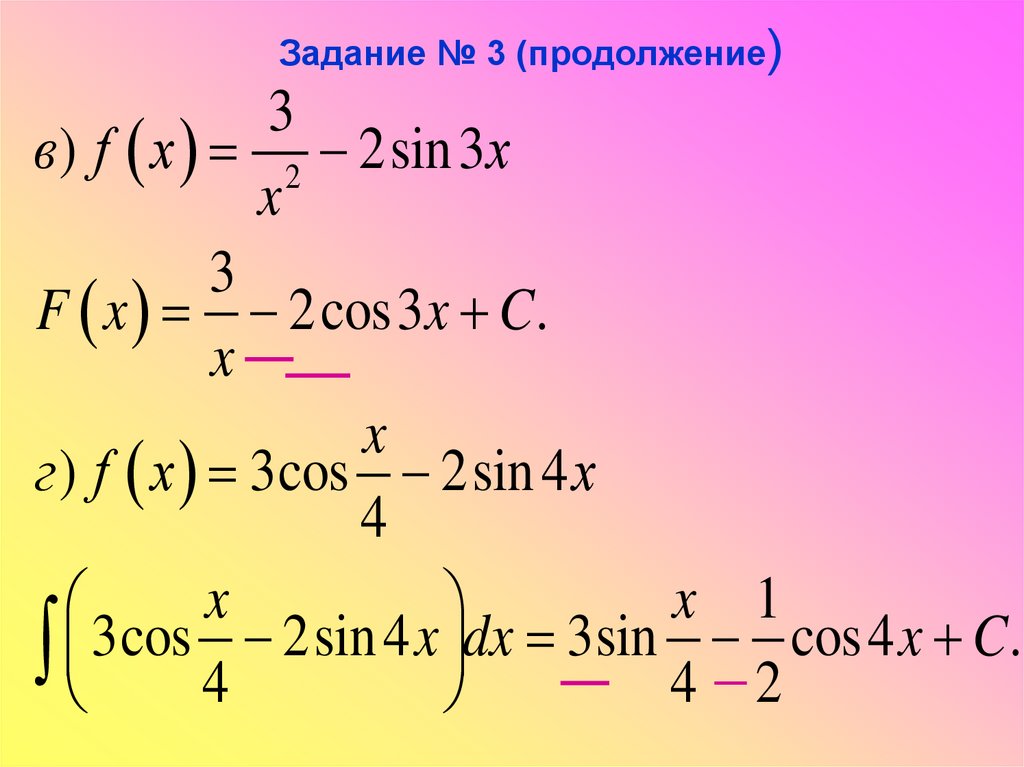









 Математика
Математика








