Скалярное произведение векторов. Определение 1

1.

§3. Скалярное произведение
векторов
Определение 1.
Скалярным произведением векторов a
и b называется число a b a b cos , где
- угол между векторами a и b .

2.

Свойства скалярного
произведения векторов
1. a b b a ,
2. a a a
2
; a
a
2
,
3. a b c a b a c ,
4. a b a b a b ,
5. a b 0 a 0 или b 0 или a b 0 .

3.

Теорема. Если a a1 , a2 , a3 , b b1 , b 2, b 3 ,
то в базисе i, j, k скалярное произведение
a b a1b1 a2b2 a3b3 .
Угол между векторами
определяется по формуле:
cos
a b
a b .
a
и
b

4.

§4. Векторное произведение
векторов
Определение 1.
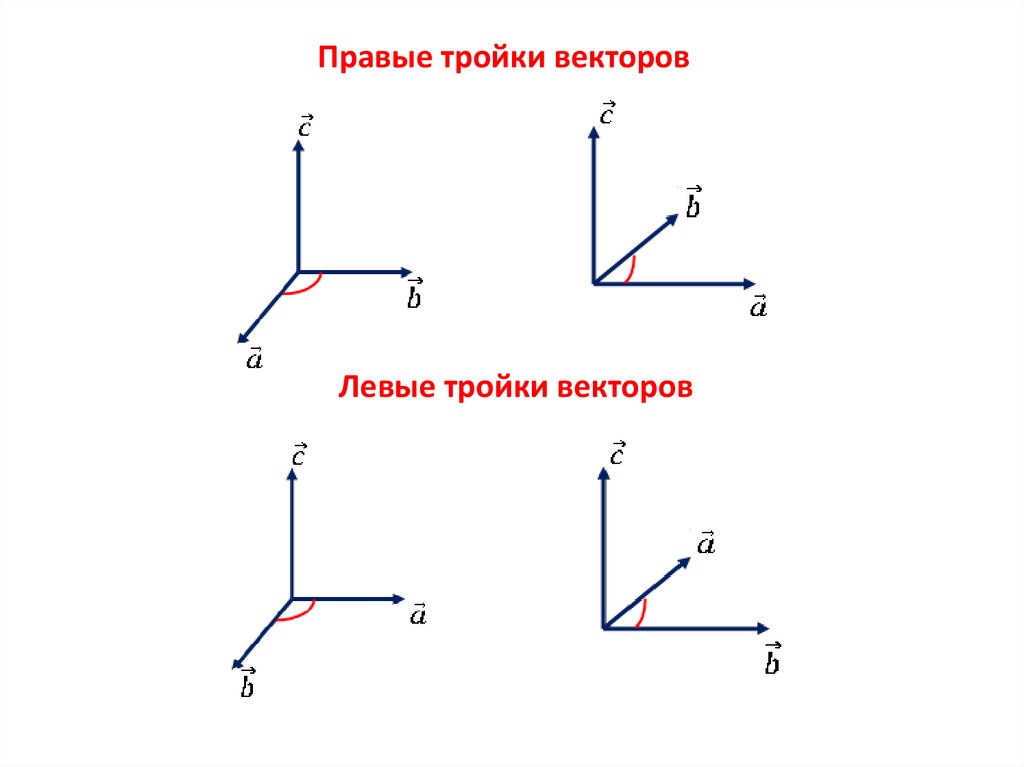
Упорядоченная
тройка
некомпланарных векторов называется
правой, если после приведения их к
общему началу из конца третьего
вектора кратчайший поворот от первого
ко второму виден совершающимся
против часовой стрелки. Иначе тройка
называется левой.

5.

Правые тройки векторов
Левые тройки векторов

6.

Определение 2.
Векторным произведением векторов a
b
с a b
и
называется
вектор
удовлетворяющий условиям:
1. с a и с b ;
2. c a b a b sin ;
3. векторы a , b , с a b
"правую тройку" векторов.
образуют

7.

Свойства векторного
произведения векторов
1.
2.
3.
4.

8.

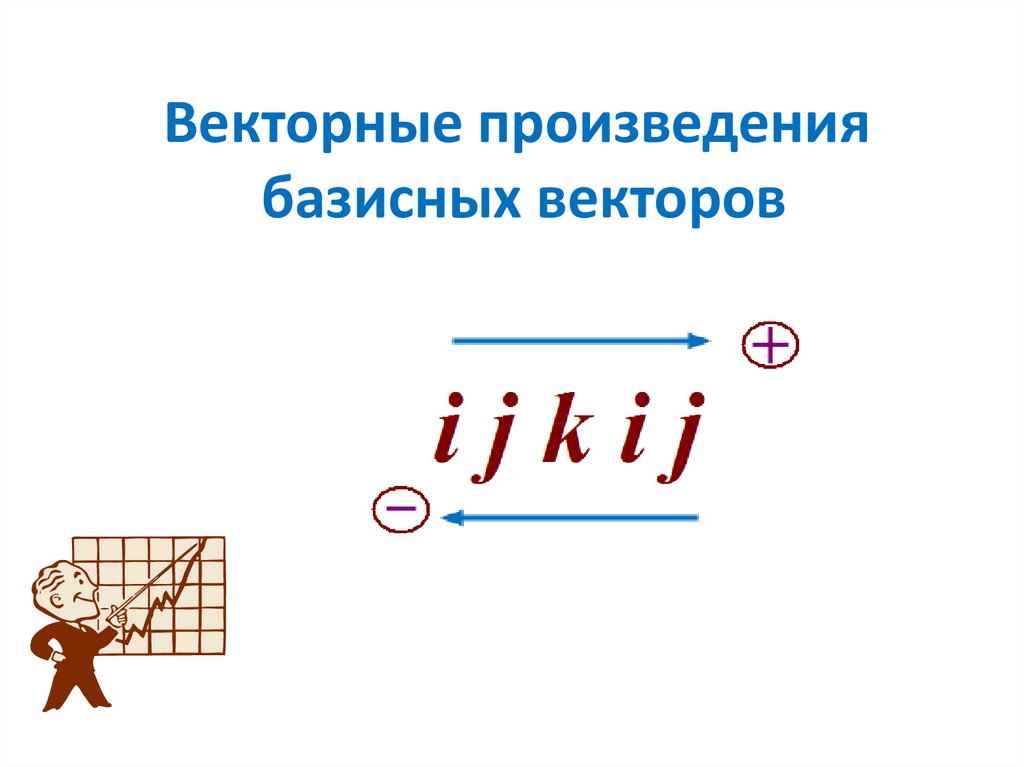
Векторные произведения
базисных векторов

9.

Теорема. Если a a , a , a , b b1 , b2 , b3 , то
векторное произведение находится по
формуле:
1
2
3
i j k
с a b a1 a2 a3
b1 b2 b3 .

10.

Применение векторного
произведения
Длина вектора с a b численно равна
площади параллелограмма, построенного
на векторах a и b .
Sпар. a b ;
1
S a b
.
2

11.

§5. Смешанное произведение
векторов
Определение.
Смешанным
произведением
трех
векторов a , b и c называется число, равное
abc a b c .

12.

Свойства смешанного
произведения
1. Если в смешанном произведении
какой-нибудь из векторов умножить на
действительное число λ, то все смешанное
произведение умножиться на это число λ.
2. abc a b c a b c .

13.

3. abc 0 тогда и только тогда, когда
векторы компланарны (т.е. лежат в одной
плоскости или в параллельных плоскостях).
4. Если abc 0 , то векторы a , b и c
образуют базис в трехмерном пространстве.

14.

Теорема. Если a a , a , a , b b , b , b ,
c c , c , c ,
то смешанное произведение
вычисляется по формуле:
1
1
2
2
3
3
a1 a2 a3
abc b1 b2 b3
c1 c2
.
c3
1
2
3

15.

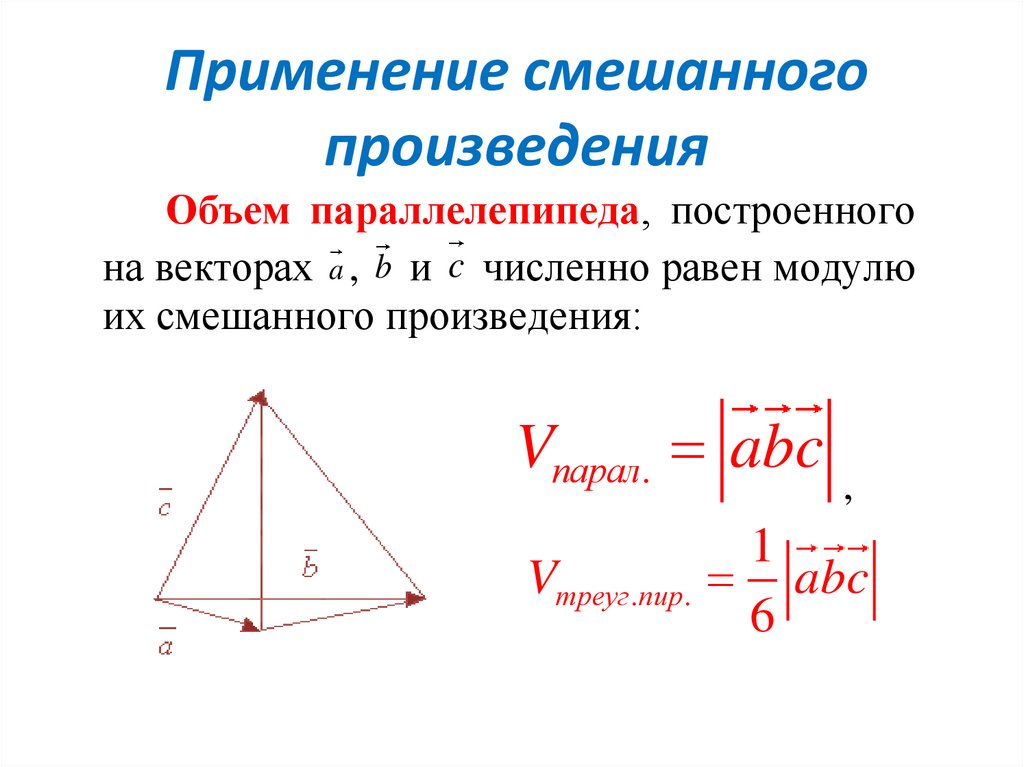
Применение смешанного
произведения
Объем параллелепипеда, построенного
на векторах a , b и c численно равен модулю
их смешанного произведения:
Vпарал. abc
,
1
Vтреуг .пир. abc
6