Похожие презентации:
Вектора. Пространства. Скалярное, векторное и смешанное произведение векторов
1. Вектора. Пространства . Скалярное, векторное и смешанное произведение векторов
2. Векторы в пространства.
Определения:1. Вектором называется направленный отрезок AB с началом в т. A и
концом в т. B .
2. Длиной (модулем) AB вектора AB называется длина отрезка AB .
3. Векторы называются равными, если они имеют одинаковые модули
и одно и то же направление.
3.
Из определения 3 следует, что любой вектор можно передвигатьпараллельно самому себе.
1. Векторы, лежащие на одной прямой или параллельных прямых называются
коллинеарными (параллельными) и обозначаются a b
2. Если точки A и B совпадают, то AB 0 или AB 0 - нулевой вектор.
3. Если e 1 , то e - единичный вектор.
4. Векторы a , b , c называются компланарными, если они лежат в одной
плоскости, или находятся в параллельных плоскостях.
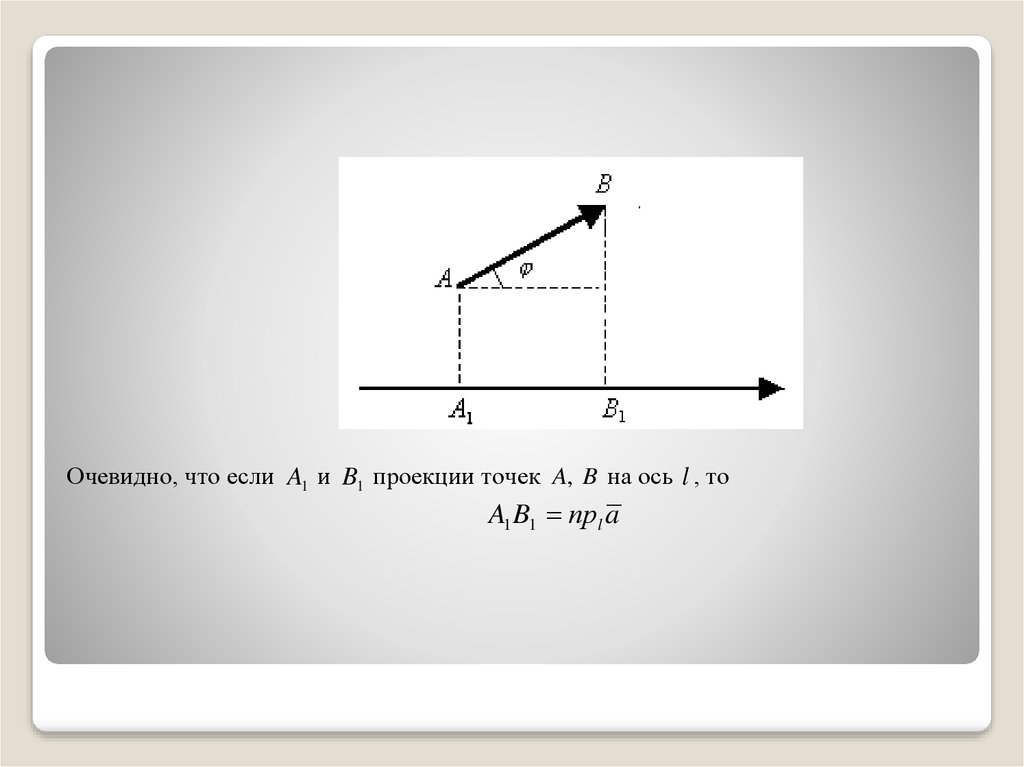
5. Проекцией вектора a AB на ось l называется величина
прl a a cos ,
где - угол между направлениями оси l и вектора a
4.
Очевидно, что если A1 и B1 проекции точек A, B на ось l , тоA1 B1 прl a
5.
9. Произведением a числа на вектор a , называется вектор, модуль которого равенa , а направление совпадает с a , если 0 , и про-
тивоположно a , если 0
Очевидно, что
а) Если a
b , то существует число , что a b ,
б) Если a
l и l 1 , то
a a l или a a l
10. Два вектора складываются по правилу параллелограмма.
Очевидно, что базисом в R2 могут быть любые два неколлинеарных вектора, а в
любые три некомпланарных вектора.
R3 -
6. Прямоугольная декартовая система координат
Определение 15. Направляющими косинусами вектораa
cos , cos , cos , где , , углы, составляющие вектором
координатными осями OX , OY , OZ .
называются числа
a
соответственно с
Направляющие косинусы
ay
ax
a
cos , cos , cos z .
a
a
a
Отсюда следует
cos cos cos 1 .
2
2
2
З а м е ч а н и е 1. Так как три координаты (две координаты в R2 ) однозначно
определяют вектор, то многие геометрические задачи можно решать аналитически (через
совокупность координат).
7. Скалярное произведение векторов
Определение 16. Скалярным произведением векторов a и b называется числоa b , вычисляемое по формуле
a b ab cos , a , b .
Так как b cos прa b , то a b a прa b
Свойства скалярного произведения
1. Если
a b , то a b 0 .
a a a2
3. a b b a
4. a b c a b b c
m a b ma b a mb .
2.
(4)
8.
З а к л ю ч е н и е. С помощью скалярного произведения определяются:1. Перпендикулярность двух векторов
a b a x bx a y b y a z bz 0
(6)
2. Косинус угла между векторами
a b
cos
a b
a x bx a y b y a z bz
a x2 a 2y a z2 bx2 b y2 bz2
(7)
3. Проекцию одного вектора на другой
прa b
a b
a
(8)
З а м е ч а н и е 2. Все вышеприведенные определения и формулы верны и в
только отбросить координату .
z
R2 . Надо
9. Векторное произведение векторов
Определение 17. Векторным произведением вектора a на bс a b a ; b , определяемый по правилу:
1.
назовем вектор
c a b ab sin , a , b , o ,
(9)
1.
с a , c b
2.
с
направлен в ту сторону от плоскости, образуемой векторами a и b , так, чтобы
кратчайший поворот от a к b был против часовой стрелки, если смотреть с конца
вектора с .
10.
Свойства векторного произведенияa b , то a b 0 .
a b b a
a b c a b b c
m a b ma b a mb .
1. Если
2.
3.
4.
11. Смешанное произведение векторов
Определение 18. Смешанным произведением векторов a , b и c называется число,равное скалярному произведению векторов a b и c , и записывается в координатной
форме
ax a y az
a b с bx b y bz
cx c y cz
Так как a b с a b c , то смешанное произведение записывается в виде a b с .
Рассмотрим параллепипед, построенный на векторах a , b , с . Так как S a b , а
h прd c , где d a b , и a b с a b пр d c , то V a b с .
12.
З а м е ч а н и е . С помощью смешанного произведения определяются:1. Компланарность 3-х векторов
ax a y az
a b с bx b y bz 0
cx c y cz
(13)
2. Объем параллелопипеда, построенного на векторах a , b , с
V a b с
(14)











 Математика
Математика








