Скалярное произведение векторов

1.

СКАЛЯРНОЕ
ПРОИЗВЕДЕНИЕ
ВЕКТОРОВ
Геометрия 9 класс

2.

Вектор – направленный
отрезок
Y
a xa ya
yb
ya
xb
O
a
aиb
xa
X
b xb yb

3.

Координаты вектора с концами в точках A(xA, yA) и
B(xB, yB) :
AB
xB x A yB y A
Длина вектора a(x, y):
a
x y
2
2
Координаты суммы векторов a(xA, yA) и b(xB, yB) :
a b
xB x A yB y A
Координаты произведения вектора a(x, y) на число
λ:
a
x y

4.

Диктант
Даны точки A(2; -3), B(-1; 2),
С(0; -4)
1. Найдите координаты вектора AB
2. Найдите координаты вектора ВС
2. Найдите длину вектора AB
2. Найдите длину вектора BC
2. Произведение 5 · AB :
AB
BC
AB
BC
( 3 5)
( 1 6)
2
2
( 3) 5
2
1 ( 6)
5 AB
2
34
37
( 15 25)

5.

Угол между векторами
a
O1
a
O.
b
и
b
; a; b
AOB
A
A1
a
b
a
B1
Угол
векторами
между
aиb
b
B
a; b
Если a b ; a 0 или b 0; a 0, b 0
то 0 0
0 0 180 0

6.

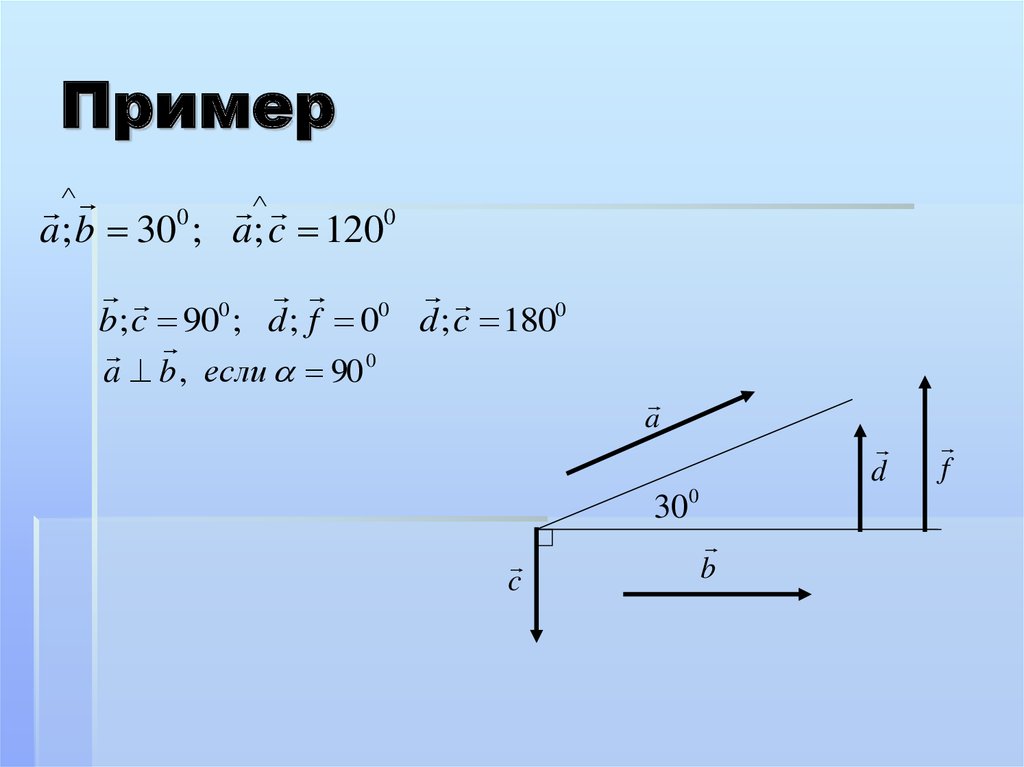
Пример
0
a; b 30 ; a; c 1200
0
0
b; c 90 ; d ; f 0 d ; c 1800
a b , если 90 0
a
d
300
c
b
f

7.

Скалярным произведением
векторов называется
произведение их длин на
косинус угла между ними
a b скалярное произведен ие _ векторов
a и b длины векторов
a
a b a b cos( )
b

8.

Примеры:
a
1.
2
b
,
a
5 b
a
1.
7 b
1.
a
1.
1. a
,
1
,
b
,
7 , b
3
,
1
,
4
,
1
,
5,
a b
0
60
0
2 3 cos 60
0
a b
0
5 1 cos 30
0
a b
7 4 cos 45
30
45
0
a b
120
0
a b
90
0
3
5 3
2
14 2
0
1 1 cos 120
0
7 5 cos 90
1
2
0

9.

b
Свойства скалярного
произведения:
a
a b 0 a b
0
a b a b a b cos 0 a b a b
b
a
0
a b 90
0
a b 90
a b 0
a b 0
a
b
b
a

10.

Свойства скалярного
произведения:
0
a b a b a b cos180 a b
a
b
a
2
a a a скалярный квадрат вектора
2
2
0
a a a a a cos 0 a

11.

Скалярным произведением
векторов a x1 y1 и b x2 y2
называется число
a b
Y
B ( x2 ; y 2 )
y2
b
x2
y1
O
A( x1 ; y1 )
a
x1
x1 x2 y1 y2

12.

Примеры: скалярное
произведение векторов
1. a( 5 4) и b( 2 1)
a b
5 2 ( 4) 1
6
1. a( 0 3) и b( 7 1)
a b
0 7 3 ( 1)
4
1. a( 5 2) и b( 4 1) a b
5 4 2 ( 1)
18

13.

Вычислите скалярное
произведение векторов:
a b
1.
a(1,1); b(1,2)
1.
a(-2,5); b(-9,-2) a b
1.
a(-3,4); b(4,5)
1.
a(5,2); b(-9,4)
1.
a(-1,1); b(1,1)
a b
a b
a b
1 1 1 2
3
2 ( 9) 5 ( 2)
3 4 4 5
5 ( 9) 2 4
1 1 1 1
8
8
37
0

14.

Следствия
Следствие 1: a 0 и b 0, то a b x1 x2 y1 y2 0
a b
Следствие 2 : a b a b cos cos
a b
cos
x1 x2 y1 y2
x y x y
2
1
2
1
2
2
2
2

15.

Пример. Даны 2 вектора:
1. Вычислите скалярное
произведение векторов:
2. Вычислите длину
вектора a:
3. Вычислите длину
вектора b:
4. Вычислите косинус угла
между векторами:
5. Сделайте вывод: тупой,
прямой или острый угол
мы получили
a( 1 3) b( 5 2)
a b
a
b
cos a b
1 5 3 2
2
2
2
2
1 3
5 2
11
10 29
cos a b 0
11
10
29
11
290
угол острый

16.

Вычисление угла между
векторами с координатами:
a (a1, a2), b (b 1, b2)
a b a1 b1 a2 b2
1. Вычислить скалярное
произведение векторов:
2
2
a
a1 a2
2. Вычислить длину вектора a:
2
2
b
b1 b2
3. Вычислить длину вектора b:
4. Найти произведение длин
a b
векторов:
5. Разделить скалярное
a b
cos a b
произведение векторов на
a b
произведение их длин:

17.

Домашнее задание:
§§101 – 103,
вопросы №№ 13 - 18,
задачи №№ 1044 (в), 1047 (в),
1048 (для углов В и С), 1066.