Устойчивость ЛСС

1.

Автоматика и управление
Тема 5. Устойчивость ЛСС
Лекция 5. Определение устойчивости ЛСС. Основное
(необходимое и достаточное) условие устойчивости ЛСС.
Необходимый критерий устойчивости ЛСС. Признак структурной
неустойчивости. Критерий устойчивости Рауса-Гурвица.
Графоаналитический критерий устойчивости А.В.Михайлова.

2.

5.1. Определение устойчивости ЛСС
Устойчивость является понятием, определяющим необходимое условие
работоспособности АС. Если система неустойчива, значит она
неработоспособна.
Под работоспособностью АС понимается способность
системы обеспечивать зависимость (определяемую целью
управления) выходного сигнала АС от задающего
воздействия.
а) Система неустойчива;
б) после прекращения действия возмущающей силы, шарик остановится в
некоторой произвольной точке. Система находится на границе
устойчивости (нейтральная);
в) вернется в некоторую окрестность исходной точки. Система устойчива.
г) возвратится в исходное положение. Система называется
асимптотически устойчивой.

3.

АС называется устойчивой ,если будучи
выведенной из состояния покоя или
невозмущенного движения некоторым
возмущением, она вновь возвратиться в
исходное состояние покоя или
невозмущенного движения после
прекращения действия возмущения.

4.

Устойчивость бывает разная
Если рассматривается только выход системы при различных
ограниченных входах, говорят об устойчивости «вход-выход»
часто изучают устойчивость автономной системы, на которую
не действуют внешние сигналы (все входы нулевые).
Предполагается, что систему вывели из положения равновесия
(задали ненулевые начальные условия) и «отпустили».
Система, которая сама возвращается в исходное положение
равновесия, называется устойчивой.
Если при этом рассматривается только выход системы (а
не ее внутренние сигналы), говорят о «технической
устойчивости» (или устойчивости по выходу).
Внутренняя или математическая устойчивость означает,
что не только выход, но и все внутренние переменные
(переменные состояния) приближаются к своим значениям в
положении равновесия.

5.

Формальное определение внутренней устойчивости было
введено в работах А.М. Ляпунова, поэтому такое понятие
устойчивости принято называть устойчивостью по Ляпунову.
В некоторых задачах основной рабочий режим – это
периодические колебания, поэтому можно рассматривать
устойчивость процессов, а не только положения равновесия.
Лучше, конечно, если система не просто устойчива, а еще и
возвращается в положение равновесия , то есть, x(t) стремится
к x* при t→∞ . В этом случае говорят об асимптотической
устойчивости.

6.

ЛСС называется устойчивой, если при нулевых входных
сигналах и любых ненулевых начальных условиях свободная
составляющая выходного сигнала системы с течением
времени стремится к нулю:
y( t ) lim yс ( t ) 0
t
Устойчивым ЛСС присущи общие свойства:
1. Весовая функция устойчивой ЛСС g(t) при неограниченном
увеличении времени стремится к нулю:
lim g( t ) 0
t
2. Переходная функция устойчивой ЛСС, при неограниченном
увеличении времени, стремится к конечному установившемуся
значению, определяемому равенством:
lim
h(t ) Ф( p)
t
p 0
Ф(0) const ,

7.

5.2. Основное (необходимое и достаточное) условие
устойчивости ЛСС
Одномерная ЛСС
рационального вида:
с
передаточной
функцией
B( p )
B( p )
Ф( p )
A( p ) a n ( p p1 )( p p2 ) ( p pn )
Ф(p)
(1)
устойчива тогда и только тогда, когда вещественные
части всех корней p1,...,pn ее характеристического
уравнения А(p) = 0 отрицательны:
Re[pi ] < 0, i = 1, n
а сами корни pi при этом, называют устойчивыми.
В случае, если условие (2) не выполняется, ЛСС с
передаточной функцией вида (1) неустойчива.
(2)

8.

Неустойчивая ЛСС находится на границе устойчивости,
если среди корней p1 ,...,pn ее характеристического полинома
A(p) есть корни с отрицательными и хотя бы один pk корень с
нулевой действительными частями:
Re[pk ] = 0,
корень pk при этом называют нейтральным.
Значения параметров системы, при которых она находится
на границе устойчивости, называются критическими.

9.

10.

Если корни A(p) известны, то вопрос об устойчивости АС решается
просто. Однако процесс определения корней очень трудоемкий,
особенно для систем высокого порядка (n > 3). Поэтому для оценки
устойчивости АС используют различные критерии устойчивости.
jI
R
jI
jI
R
Re[pi] <0
Re[pl ] =0
АС устойчива
АС на границе устойчивости
Re[pl ] >0
АС неустойчива
Критериями устойчивости называются правила, позволяющие
исследовать устойчивость АС без непосредственного нахождения
корней характеристического уравнения

11.

5.3. Необходимый критерий устойчивости ЛСС
ЛСС с передаточной функцией Ф(p) рационального вида
может быть устойчива только тогда, когда все
коэффициенты ai ее характеристического полинома A(p)
положительны:
ai > 0, i = 0 , n
Ф( p )
Ф( p )
( 5 p 1)
- АС может быть как устойчивой, так и не
3 p 3 2 p 2 p 1 устойчивой. Для оценки устойчивости необходимы
дальнейшие исследования.
( 5 p 1)
3 p3 p 1
АС не может быть устойчивой, так как а2= 0

12.

5.4. Признак структурной неустойчивости ЛСС
Устойчивость АС зависит от структуры системы и значений
параметров ее элементов.
Системы, которые, при заданной структуре, никакими
изменениями значений параметров ее элементов не могут
быть переведены в область устойчивости называются
структурно неустойчивыми

13.

Для следящих систем
X(p)
W(p)
Y(p)
Другими словами, если
прямой тракт АС содержит на
два и более интегрирующих
звеньев больше чем
форсирующих, то система
структурно неустойчива.
признаком структурной неустойчивости является условие:
число интегрирующих звеньев v в передаточной функции
разомкнутой системы
m
вi p i
B( p ) i 0
B( p )
W( p )
n
~
C( p )
p C( p )
Ci p i
i 0
превышает на два и более порядок полинома числителя,
то есть условие: v m + 2

14.

X(p)
W( p )
W(p)
Y(p)
W ( p)
Ф( p )
1 W ( p)
K
~ 2 ~
~
p ( C 2 p C1 p C0 )
2
~ 2 ~
~
A( p ) p ( C 2 p C1 p C0 ) K a4 p 4 a3 p 3 a 2 p 2 a0
2
~
~
~
a 4 C 2 , a 3 C 1 , a 2 C 0 , a1 0 ; a0 K .
замкнутая АС не устойчива, так как коэффициент a1 = 0

15.

5.5. Критерий устойчивости Рауса - Гурвица
В 1877 году Раус, а в 1895 году Гурвиц
аналитический критерий, позволяющий установить факт
принадлежности корней pi A(p) к левой полуплоскости
комплексной плоскости.
Суть метода состоит в проверке n неравенств, которым должны
удовлетворять коэффициенты ai характеристического
полинома замкнутой системы:
Наиболее распространенный в литературе вариант:
A( p) a0 p a1 p
n
n 1
an 1 p an
1
Внимание!!! Нумерация коэффициентов изменена в
обратном порядке

16.

A( p) a0 p a1 p
n
n 1
an 1 p an
1
Для получения этих неравенств составляются:
1. Матрица Гурвица R - квадратная матрица n-го порядка,
составляемая из коэффициентов ai характеристического
полинома A(p) по правилам:
На главной диагонали выписываются
элементы а1, а2,..., аn. Затем при
a1 a3 a5 0
движении от этих элементов вверх
a a a 0
размещаются коэффициенты в порядке
возрастания индексов, при движении
0 2 4
вниз — в порядке убывания.
R 0 a a 0
Вместо отсутствующих
коэффициентов записываются
нули
1 3
0 0 ... an

17.

Главные миноры определителя n
a1
a1 a3
a
R1 a1 ; R2
;
R
3
0
a
a
0 2
0
включая сам определитель
определителями Гурвица.
n
a3
a2
a1
a5
a4 ; ....
a3
, называют
Для того чтобы система была устойчива, необходимо и
достаточно, чтобы определители Гурвица, составленные из
коэффициентов ее характеристического уравнения, при ао > 0
были больше нуля:
a0 0, 1 0, 2 0, ..., n 0
Если хотя бы один из определителей i 0 - ЛСС
неустойчива.

18.

Вариант с обычной нумерацией коэффициентов:
n
A( p ) ai p i a n p n a n 1 p n 1 a1 p 1 a0 .
i 0
a0 0 0 0
а) по главной диагонали слева
a a a 0
направо записываются
2 1 0
коэффициенты, начиная с a0 до
a4 a3 a 2 a1 0
an-1 в порядке возрастания
R
индекса при переходе от левого
0 0 a
столбца к правому
n 1 a n 2 a n 3
0 0 0 a n a n 1
б) дополняются строки матрицы:
- вправо и влево от элементов главной диагонали в каждой
строке из выражения A(p) записываются коэффициенты ai в том
же порядке, как они расположены в характеристическом
полиноме. Вместо отсутствующих коэффициентов
записываются нули

19.

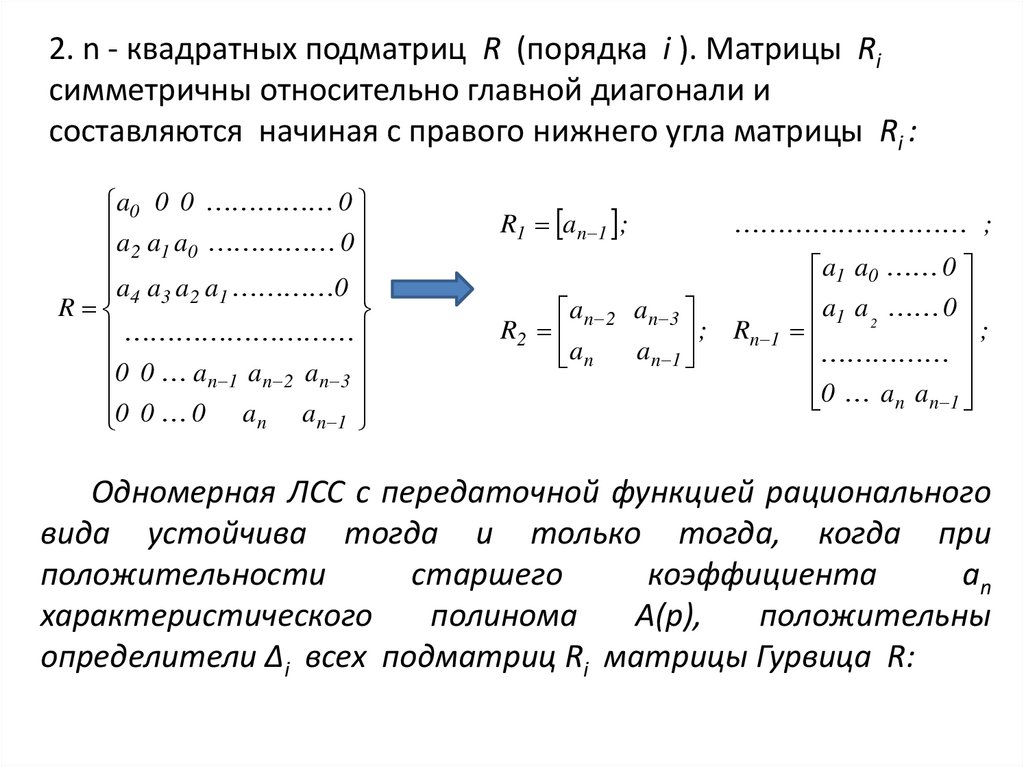
2. n - квадратных подматриц R (порядка i ). Матрицы Ri
симметричны относительно главной диагонали и
составляются начиная с правого нижнего угла матрицы Ri :
a0 0 0 0
a a a 0
2 1 0
a4 a3 a 2 a1 0
R
0 0 a
n 1 a n 2 a n 3
0 0 0 a n a n 1
R1 a n 1 ;
;
a1 a0 0
a a 0
a n 2 a n 3
1 2
;
R2
;
R
n 1
a n 1
a n
0
a
a
n n 1
Одномерная ЛСС с передаточной функцией рационального
вида устойчива тогда и только тогда, когда при
положительности
старшего
коэффициента
аn
характеристического
полинома
A(p),
положительны
определители Δi всех подматриц Ri матрицы Гурвица R:

20.

Правила Вышнеградского
ЛСС третьего порядка устойчива, если произведение
средних, больше произведения крайних коэффициентов
характеристического полинома АС.
A( p) a3 p a2 p a1 p a0
3
2
a2 a1 a3 a0
1

21.

5.6. Графоаналитический критерий устойчивости
А.В. Михайлова
Устойчивость систем более высокого порядка (n > 5)
анализируется с помощью частотных (графоаналитических)
критериев, определяющих необходимое и достаточное
условие устойчивости ЛСС с передаточной функцией Ф(p)
рационального вида . К их числу относятся:
- критерий Михайлова (1938г.);
- критерий Найквиста (1932г.).
Основная идея использования графоаналитического
критерия Михайлова заключается в определении полного
угла поворота A радиус-вектора Михайлова A(j )
(характеристического годографа) характеристического
полинома системы A(p) при изменении частоты от 0 до .

22.

Для характеристического полинома n-го порядка
A(p) = an pn+an-1 pn-1 +...+a1 p+a0
годограф A(j ) определяется равенством:
A(j ) = an(j )n +...+ a2(j )2+ a1(j ) + a0 = R( ) +jI( ),
где R( ) = a0 – a2 2+ a4 4 – a6 6+...- вещественная часть
годографа,
I = (a1- a3 2+ a5 4 – a7 6+...) - мнимая часть годографа.
При выполнении необходимого критерия устойчивости ( ai > 0,
i =0 , n ), начало характеристического годографа ( =0)
определяется координатами: R(0) = a0 > 0, I(0) = 0,
Характеристический годограф A(j ) для всех ЛСС,
удовлетворяющих необходимому критерию
устойчивости, начинается с точки, лежащей на
положительной вещественной полуоси.

23.

Текущий угол радиус-вектора годографа A(j ) :
I( )
( ) = argA(j ) = arctg
.
R( )
Полный угол поворота A радиус-вектора характеристического
годографа:
A = ( ), [0 ]

24.

Теорема Михайлова.
Для любого многочлена комплексной переменной p nго порядка:
n
A( p ) ai p i
i 0
полный угол поворота A радиус- вектора его годографа
A(j )= A( p ) p j
A=
определяется равенством:
2
( n v 2 )
где v- число нейтральных корней полинома A(p) (корней с
нулевой действительной частью);
- число неустойчивых корней полинома A(p) (корней с
положительной вещественной частью).

25.

Формулировка критерия Михайлова.
Одномерная ЛСС с передаточной функцией Ф(p)
рационального вида устойчива тогда и только тогда, когда
полный угол поворота А радиус-вектора ее
характеристического годографа A(j ) при изменении
частоты от 0 до определяется равенством:
A
где n - порядок АС.
2
n,
=0 =0
A= ( n v 2 )
2
Годограф A(j ) устойчивой АС берет начало на
положительной полуоси комплексной плоскости в точке а0
и последовательно проходит в положительном
направлении n квадрантов.

26.

jI
jI
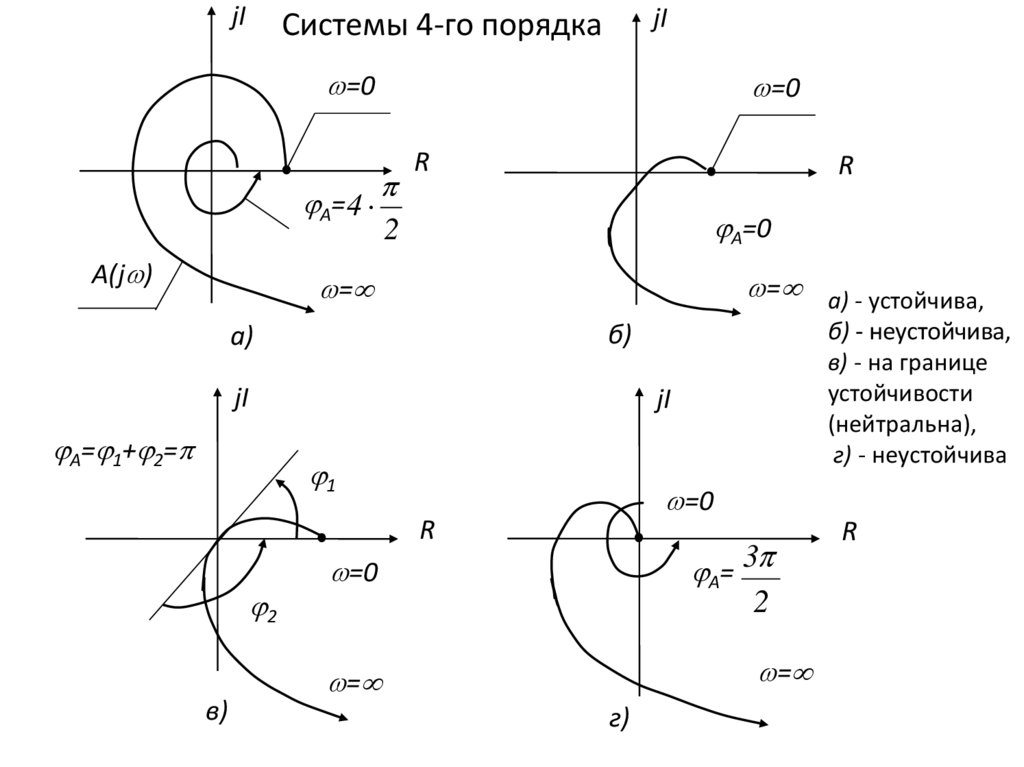
Системы 4-го порядка
=0
A= 4
A(j )
=0
R
R
A=0
2
= а) - устойчива,
=
jI
jI
A= 1+ 2=
1
=0
R
2
в)
б) - неустойчива,
в) - на границе
устойчивости
(нейтральна),
г) - неустойчива
б)
a)
A= 3
=0
2
=
=
г)
R

27.

Следствие критерия Михайлова
(условие перемежаемости корней)
При последовательном прохождении годографом устойчивой системы A(j )
в положительном направлении n-квадрантов комплексной плоскости, он
поочередно пересекает ее действительную и мнимую координатные оси:
1
A(j )
2
jI
1
=0
n=5
=0
R
условием чередуемости
(перемежаемости) корней i
и i , то есть условием:
1 < 1 < 2 < 2 < 3 < . . .
2
Частоты i, соответствующие точкам пересечения годографа с
действительной осью, удовлетворяют равенству I( i )=0 и являются
корнями мнимой части I( ) годографа A(j ). Частоты , соответствующие
точкам пересечения годографа с мнимой осью, удовлетворяют равенству
R( i )=0 и являются корнями действительной части R( ) годографа A(j )

28.

ЛСС устойчива тогда и только тогда, когда корни
вещественной R( ) и мнимой I( ) частей
характеристического годографа A(j ), расставленные в
порядке возрастания, чередуются между собой, а общее их
количество равно порядку системы n.