Похожие презентации:
Предел функции
1.
ПРЕДЕЛ ФУНКЦИИСмотреть видео заставку
2.
23.
§1 Понятие предела функцииКонечный предел функции при x x 0
Пусть функция y=f(x) определена в
проколотой окрестности точки x0 т.е.
.
на множестве 0 ( x0 ) x 0 x x0 .
В точке x0 значение функции f ( x0 ) может
быть не определено.
Приведем определение предела функции при
на языке последовательностей (по Гейне).
V. Khudenko
3/24
4.
Эдуард Гейне 1821 - 18814
5.
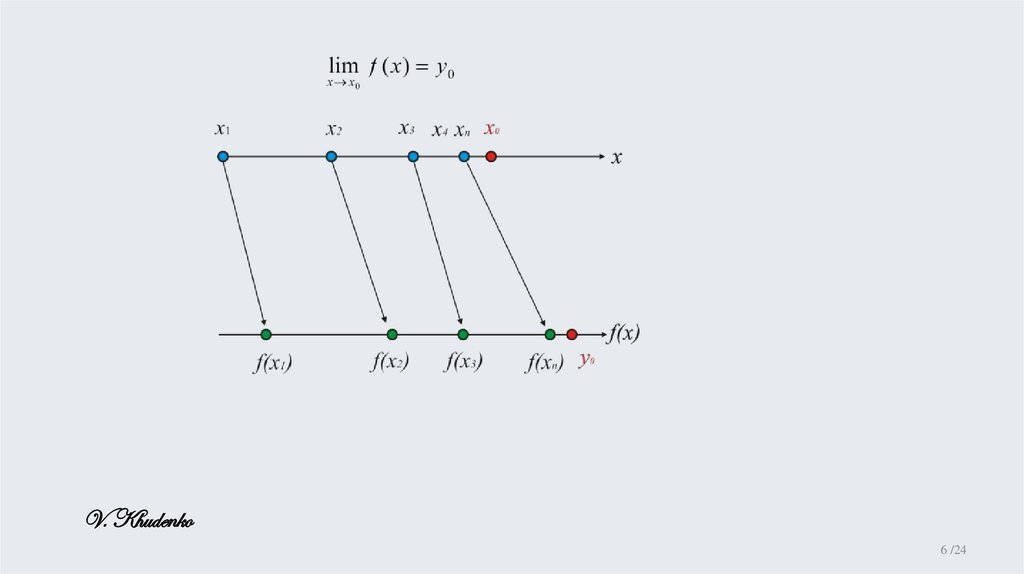
Определение 1.1. Число называется yпределом функции в точке x0 (или при x x ),
если для любой последовательности точек
x O ( x ) сходящейся к точке x0 ,
последовательность соответствующих
значений функции f x n
сходится к y 0
0
0
n
0
y0 lim f ( x) lim xn x0 lim f ( xn ) y0
x x0
n
n
Смотреть анимацию
V. Khudenko
5 /24
6.
V. Khudenko6 /24
7.
Дадим еще одно определение пределафункции при x x 0 на языке " - " (по Коши)
Огюстен Луи Коши 1789-1857
7
8.
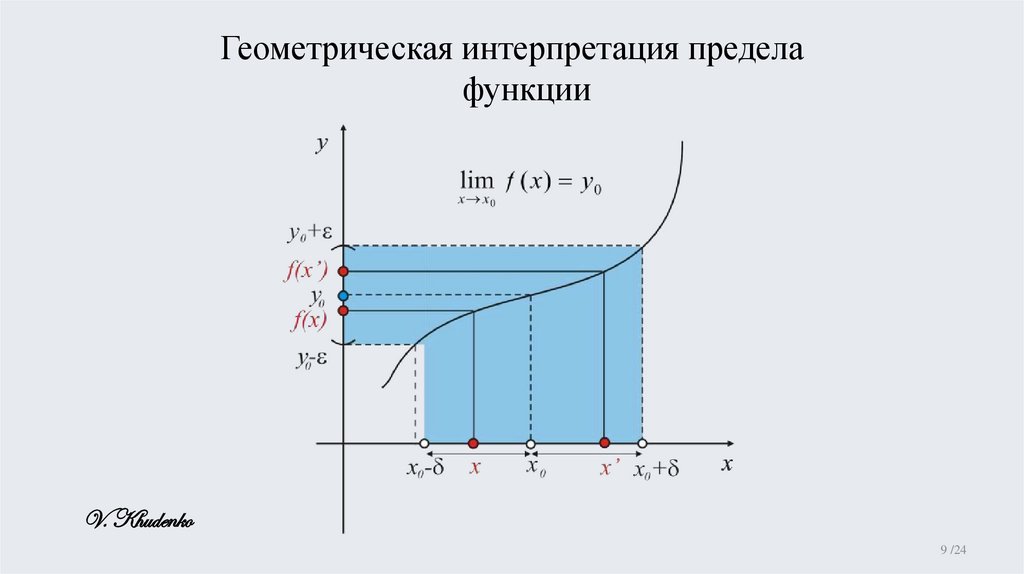
Определение 2.1. Число y0 называется пределом функции вточке x0 (или при x x ),
если для любого >0 можно указать такое
число ( ) 0 , что при всех x, удовлетворяющих условию
0 x x0 , выполняется неравенство
f ( x ) y0
0
y0 lim f ( x) 0 0 : x 0 x x0
x x0
f ( x ) y0
Смотреть анимацию
V. Khudenko
8 /24
9.
Геометрическая интерпретация пределафункции
V. Khudenko
9 /24
10.
Теорема 1.1. Определения предела функции вточке по Гейне и по Коши эквивалентны.
V. Khudenko
10 /24
11.
V. Khudenko11 /24
12.
Односторонние пределы функцииИногда приходится рассматривать предел
функции f(x) при условии, что точка x,
приближаясь к точке x0 , остаётся или
правее или левее её.
V. Khudenko
12 /24
13.
Левой окрестностью точки называетсямножество O x 0 x x x x
0
0
0
V. Khudenko
13 /24
14.
Правой окрестностью точки называетсяO x0 0 x x0 x x0
множество
V. Khudenko
14 /24
15.
Определение 3.1. Число y 0 называетсялевым односторонним пределом (пределом
слева) функции y=f(x) в точке x0 , если
0
( ) 0 : x : x0 x x0
f ( x) y0
Смотреть анимацию
V. Khudenko
15 /24
16.
Определение 4.1. Число y0 называетсяправым односторонним пределом (пределом справа)
функции y=f(x) в точке x0 , если
0 ( ) 0: x: x0 x x0 f ( x ) y0
Смотреть анимацию
V. Khudenko
16 /24
17.
Пример: Найти односторонние пределы вточке x 0 2 функции
Имеем
x 2 , x ,2
f (x ) 4
x , x 2,
x2
lim f x lim
1
x 2 0
x 2 0 4
lim f x lim x 2
x 2 0
x 2 0
V. Khudenko
17 /24
18.
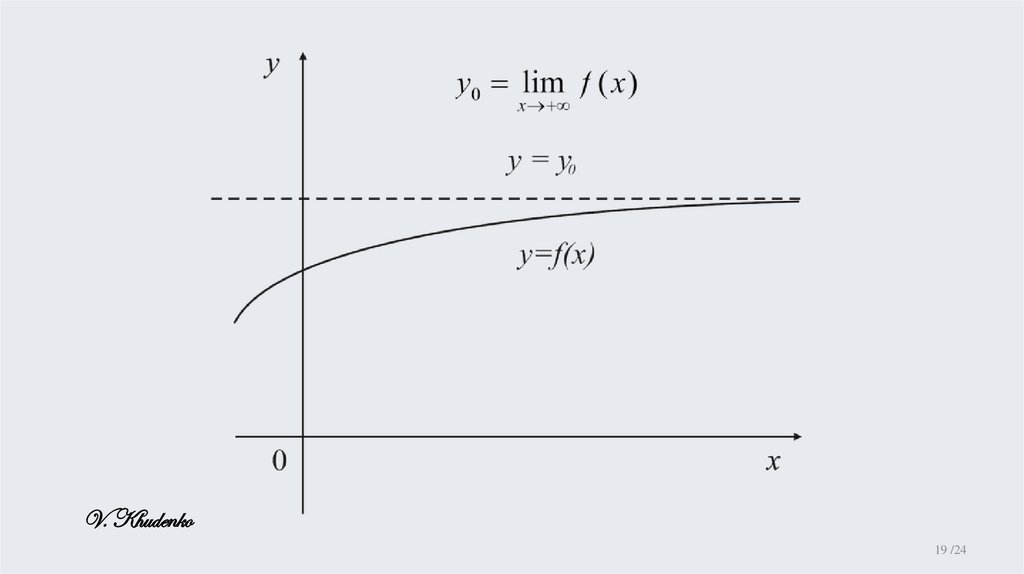
Конечный предел функции при xОпределение на языке последовательностей
y0 lim f ( x) xn : lim xn lim f xn y0
x
n
n
Определение 5.1. (на языке " - ") Число y 0
называется пределом функции при x
если
y0 lim f ( x) 0 M 0 : x M f ( x) y0
x
V. Khudenko
18 /24
19.
V. Khudenko19 /24
20.
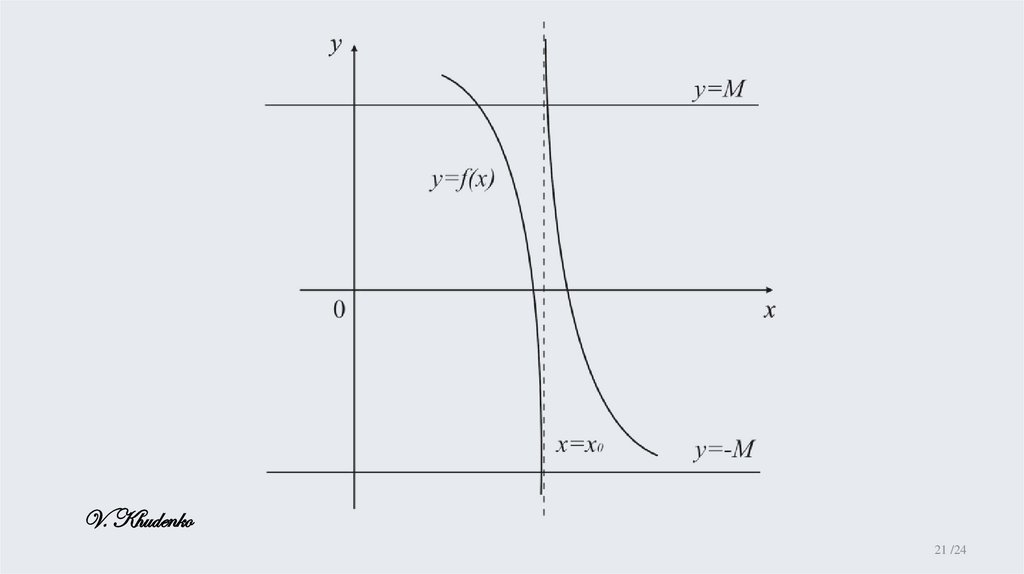
Бесконечный предел функции при x x 0Определение 6.1. Предел функции f(x) при x x 0
называется бесконечным, если для любого
положительного числа М существует
число >0, такое, что для всех значений х,
удовлетворяющих неравенству 0 x x 0
будет выполняться неравенство f ( x) M
В таком случае функцию называют
f (x )
бесконечно большой и пишут xlim
x
0
lim f ( x) M 0 0 : x, 0 x x f ( x) M
0
x x
0
V. Khudenko
20 /24
21.
V. Khudenko21 /24
22.
V. Khudenko22 /24
23.
Бесконечный предел функции при xОпределение 7.1. Предел функции y=f(x)
при x называется бесконечным,
если lim f ( x) M 0 N 0 : x, x N f ( x) M
x
V. Khudenko
23 /24



















 Математика
Математика








