Похожие презентации:
Решение системы способом подстановки
1.
«Метод решения хорош, если с самого начала мы можемпредвидеть - и далее подтвердить это, - что, следуя
этому методу, мы достигнем цели»
Г. Лейбниц
Шаповалова Вероника Николаевна
Учитель математики высшей
категории
Домодедово, 2020
2.
Решение системы способом подстановки - 4,6Решение системы способом сложения - 1,3
Решение системы способом замены переменной - 2,5
Решение систем графическим способом - 7,8
3.
Ответ: (1;2), (2;1)Симметрической называется такая
система, которая не изменится, если
переменные х и у поменять местами.
Решением такой системы являются
симметричные пары чисел (х;у) и (у;х).
4.
Решим систему:Решение:
;
;
(х;у)
(у;х)
( -у; -х)
(-х; -у)
5.
Ответ: (1;2), (2;1)Симметрической называется такая
система, которая не изменится, если
переменные х и у поменять местами.
Решением такой системы являются
симметричные пары чисел (х;у) и (у;х).
6.
Используя свойства симметрической системы, найдите все решениясистемы, одним из решений которой является пара чисел (1;3)
Решение:
система не изменится, если х и у поменять местами или
заменить на –х и –у, значит
(1;3), (3;1), (-3;-1), (-1;-3) – решения системы.
Ответ: (-3;-1), (-1;-3), (1;3), (3;1).
7.
04.12.19484 декабря – День информатики в России
8.
Диагностическая работана «3»
х+3у=5,
ху=2.
Решение:
на «4»
3х2-2у2=10,
5х2+2у2=22.
Решение:
на «5»
х2+у2=61,
х2-у2=11.
Решение:
9.
Диагностическая работана «3»
х+3у=5,
ху=2.
Решение:
х=5-3у,
у(5-3у)=2;
.
-3у²+5у-2=0; D=1;
х=5-3у,
у=1;
х=2,
у=1;
х=5-3у,
х=3,
у=⅔;
у=⅔;
Ответ: (2;1), (3; ⅔ ).
на «4»
3х2-2у2=10,
5х2+2у2=22.
Решение:
3х2-2у2=10,
8х2=32;
на «5»
х2+у2=61,
х2-у2=11.
Решение:
3х2-2у2=10,
х=±2;
х=-2,
у= ±1; (-2;-1), (-2; 1);
х=2,
у= ±1; (2;-1), (2;1);
Ответ:
Ответ: (-6;-5), (-6;5),
(-2;-1), (-2; 1); (2;-1), (2;1)
(6;-5), (6;5).
10.
При всех значениях параметра а определитечисло решений системы уравнений
у=а, 4< а
у=а, а=4
у=а, -4< а <4
у=а, а=- 4
у=а, а < -4
Ответ:
при -4< а <4 система
имеет два решения;
при а = ±4 система имеет
одно решение;
при а <-4 и а > 4 система
решений не имеет.
11.
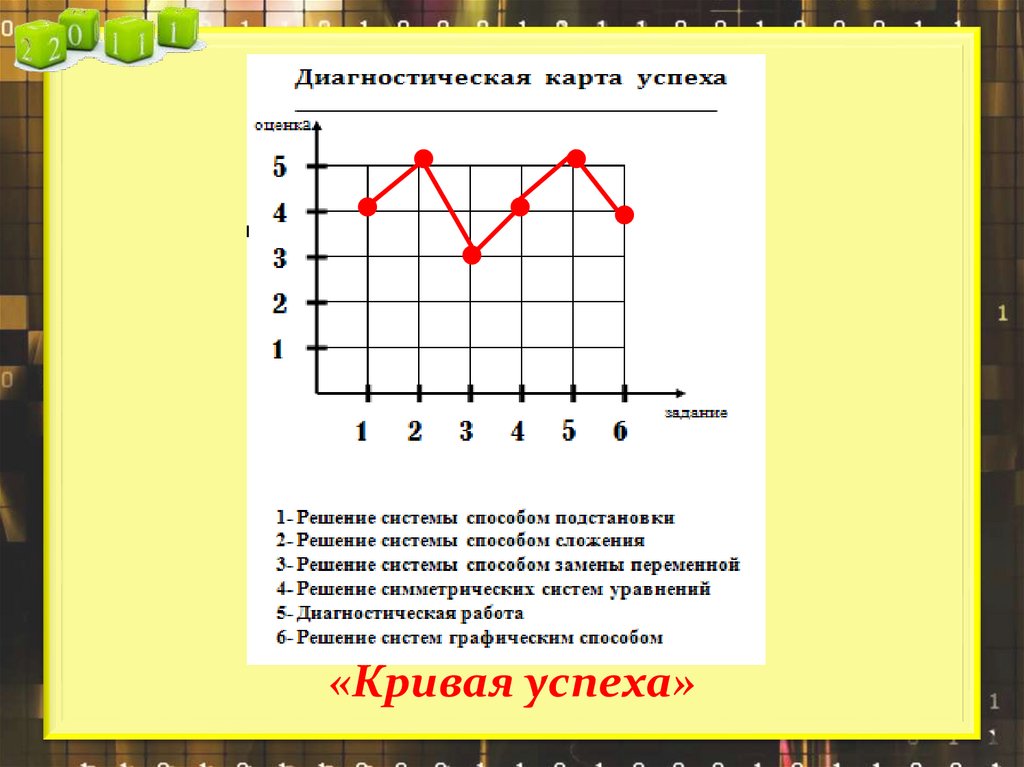
«Кривая успеха»12.
Рефлексия• Что нового вы узнали на уроке?
• Достигли ли вы поставленной цели?
• Какую цель Вы для себя поставите на
следующем этапе?
«Букет настроения урока»
13.
Задание на домИспользовать информационные ресурсы для
выбора 4 систем уравнений с двумя переменными
(на разные методы решения);
Решить две из них
(вызвавшие трудности на уроке).












 Математика
Математика








