Идея рационализации неравенств

1.

2.

Идея рационализации неравенств встречается
в математической литературе под разными
названиями:
• метод замены множителей – Голубев В.И.,
Игнатович И.К., Колесникова С.И.
• метод декомпозиции – Моденов В.П.
• обобщенный метод интервалов – Дорофеев Г.В.
и др.

3.

Метод замены множителей
при решении неравенств.
• неравенства, содержащие модуль;
• иррациональные неравенства;
• показательные неравенства;
• логарифмические неравенства.

4.

Теорема 1: неравенство f(x)>g(x) при f(x)>0 и
g(x)≥0 равносильно неравенству f²(x)>g²(x), т.е.
неравенство f(x) - g(x) >0 равносильно
неравенству f²(x) - g²(x) > 0.
Доказательство:
1.Необходимость: f(x) - g(x) >0
f²(x) - g²(x) >
0. f²(x) - g²(x) = (f(x) - g(x))(f(x) + g(x)). Так как f(x)>0 и
g(x)≥0 , то f(x) + g(x)>0; f(x) - g(x)>0 по условию,
поэтому их произведение >0 ,т.е. f²(x) - g²(x) > 0.
2. Достаточность: f²(x) - g²(x) > 0
f(x) - g(x)
>0. (f(x) - g(x))(f(x) + g(x))>0, разделим обе части на
f(x) + g(x)>0, получим равносильное f(x) чтд
g(x)>0.

5.

Неравенства, содержащие модуль.
Так как │φ(x)│≥ 0 для любого х
,то
неравенство │f(x)│ - │g(x)│ >0 равносильно
неравенству f²(x) - g²(x) > 0.
Пример 1. │х -1│< 2.
По определению:
2
-1
│х -1│- 2 < 0, (х -1)²- 2² < 0,
2
1
Замена множителей:
3
Ответ: -1< x < 3.
(х – 1– 2)(х – 1+2) < 0,
(х -3)(х +1) < 0,
Ответ: -1< x < 3.

6.

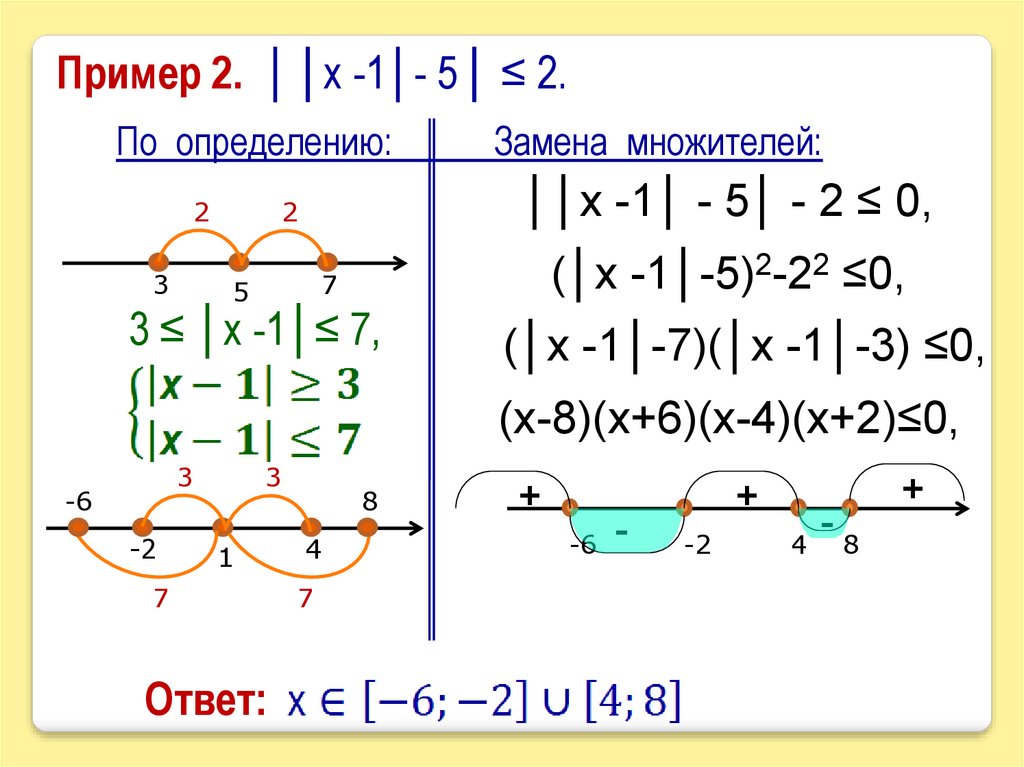
Пример 2. ││х -1│- 5│ ≤ 2.
По определению:
2
3
Замена множителей:
││х -1│ - 5│ - 2 ≤ 0,
2
(│х -1│-5)2-22 ≤0,
7
5
3 ≤ │х -1│≤ 7,
(│х -1│-7)(│х -1│-3) ≤0,
(x-8)(x+6)(x-4)(x+2)≤0,
3
-6
-2
3
1
7
Ответ:
8
4
7
+
+
+
-6 -
-2
4
-
8

7.

Пример 3. (│х -1│- 3)(│х+2│- 5)< 0.
((х – 1)² – 3²)(х+2)² – 5²)<0
(х -1-3)(х -1+3)(х+2 - 5)(х+2+5) < 0,
(х - 4)(х + 2)(х - 3)(х+7) < 0,
+
+
+
-7
-
Ответ:
-2
3
-
4

8.

9.

№6
Ответ:

10.

№4
Так как
то
,
,
Ответ:

11.

№10
Умножим на
Ответ:
, получим

12.

Иррациональные неравенства.
Рассмотрим неравенство

13.

14.

№5
Ответ:

15.

№11
Найдите сумму всех целых чисел, являющихся
решением неравенства:
В решение входят целые числа: 1и 2, сумма которых
равна 3.
Ответ: 3.

16.

№13
.
ОДЗ:
1).
2).
Ответ:

17.

Показательные неравенства.

18.

19.

№6
ОДЗ:
, учитывая ОДЗ, получаем
Ответ:

20.

Логарифмические неравенства.

21.

22.

.
№17
+
+
-2
Ответ:
-
-0,5 0 1/6 -
+
1

23.

.
№8
ОДЗ:
Ответ:

24.

№18
Ответ:

25.

.
№19
Так как
Тогда
ОДЗ: 1).
2).
Таким образом, ОДЗ:
Ответ:
С учетом ОДЗ получаем

26.

№20
Решение будем искать
при условиях:
-2
-
+
log32-2
-1 -
, откуда
+
1
Ответ:

27.

Используемая литература:
• Игнатович И.К.
Алгебра и начала анализа: пособие для поступающих в вузы.
– Минск: ТетраСистемс, 2008.
• Колесникова С.И.
Математика. Решение сложных задач Единого
государственного экзамена. – М.:Айрис-пресс, 2005.
• Колесникова С.И.
Математика. Интенсивный курс полготовки к Единому
государственному экзамену. – М.:Айрис-пресс, 2008.
• Локоть В.В., Мартынов О. М.
Решение задач ЕГЭ (2010 год): Учебное пособие. – М.:АРКТИ.
2011.
• Корянов А.Г., Прокофьев А.А.
Методы решения неравенств с одной переменной. Учебное
пособие. – М.:2010.
• Журналы: Математика в школе. Математика для
школьников.