Графики функций y = kx, y = kx+b

1.

Графики функций:
y kx , y kx b ,
k
y ,
x
Подготовила:
учитель математики
МБОУ Г.ГОРЛОВКИ «ШКОЛА № 42
Рыбина М.В.
y x

2.

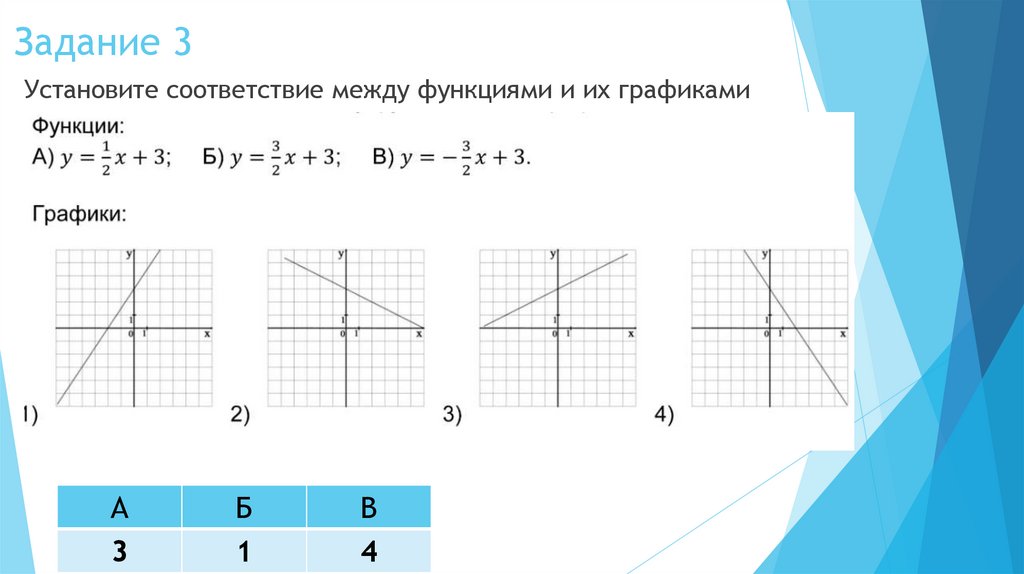
Линейная функция
Функция вида у = kx + b, где х – аргумент, k и b –
числа, называется линейной.
k 0
k 0

3.

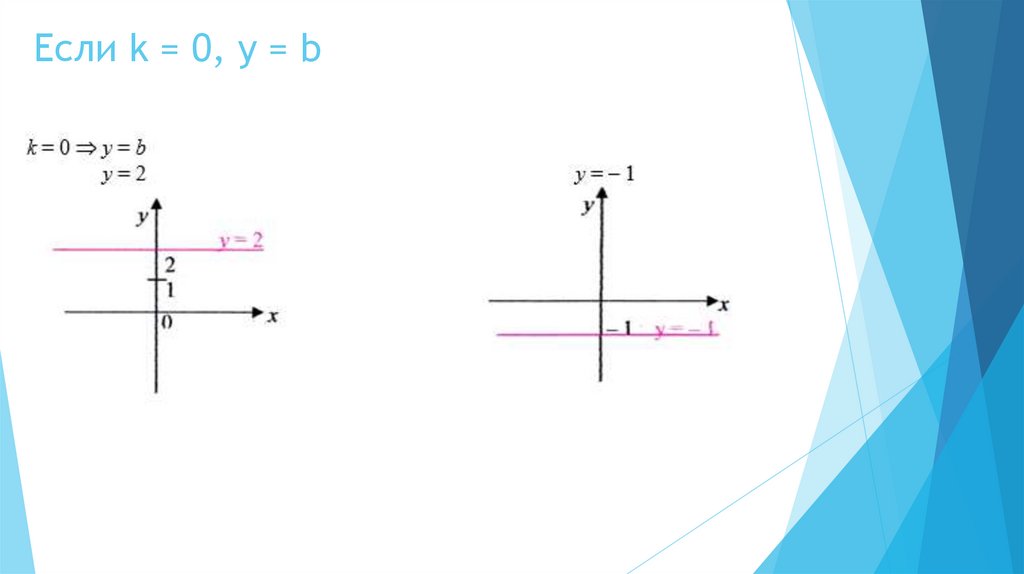
Если k = 0, y = b

4.

Прямая пропорциональность
Функция вида у = kx, где х – аргумент, k – число – прямая
пропорциональность.
k 0
k 0

5.

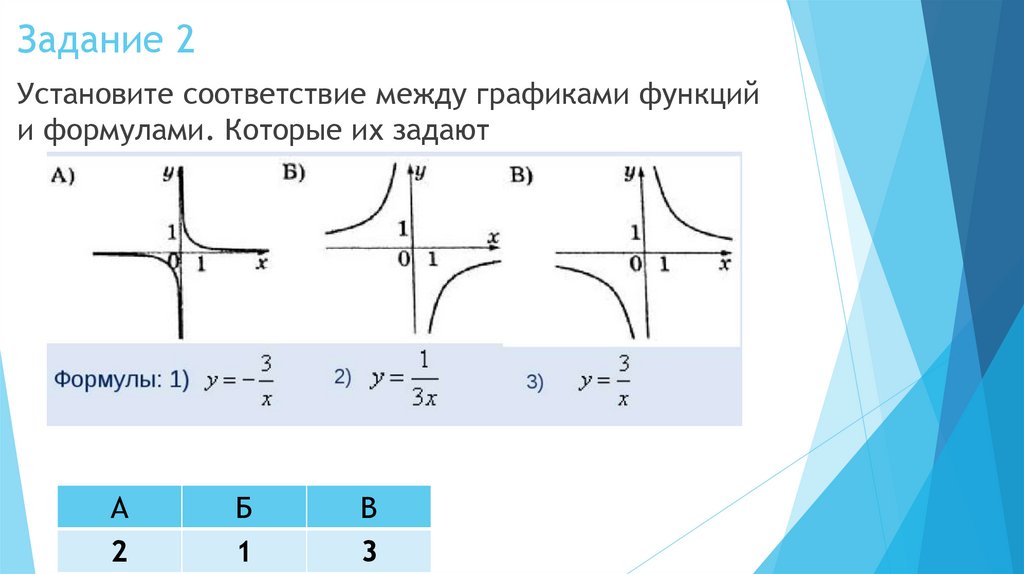
Обратная пропорциональность
k
Функция вида у = x, где х 0 называют обратной пропорциональностью.
График называется – гипербола. Она состоит из двух ветвей.
Свойства:
1. Д(у): все числа, кроме О
2. Е(у): все числа, кроме 0.
3. Нулей функции нет.
4. Промежутки знакопостоянства
Если k > 0,то у 0 при х 0
у 0 при х 0
Если k < 0, то у 0 при х 0
у 0 при х 0
5. Промежутки монотонности
Если k > 0, то график в I и III углах, убывает.
Если k < 0, то график во II и IV углах, возрастает.

6.

y x
Свойства:
1. Д(у) = R
2. Е(у) = [0; + )
3. Нули функции: у = 0 при х = 0.
4. Промежутки знакопостоянства
у 0 при х 0 и х 0.
5. Промежутки монотонности
При х 0 функция убывает.
При х 0 функция возрастает.

7.

Пример 1
6
Постройте график функции у =
x
х
у
–6
–1
–4
– 1,5
–3
–2
–2
–3
–1
–6
Найдите по графику:
Значения у, если х = 4
у = 1,5
Значения х, если у = -6
х = -1
1
6
2
3
3
2
4
1,5
6
1

8.

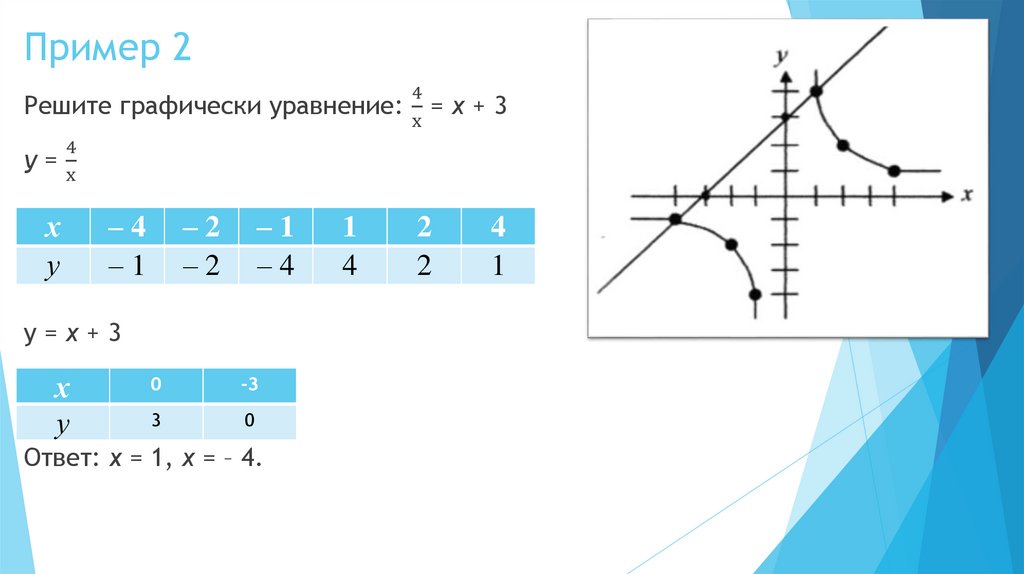
Пример 2
4
Решите графически уравнение: = х + 3
x
4
у=
x
х
у
–4
–1
–2
–2
–1
–4
у=х+3
х
у
0
-3
3
0
Ответ: x = 1, х = – 4.
1
4
2
2
4
1

9.

Пример 3
Решите графически систему уравнений: