Похожие презентации:
Алгебраические дроби
1.
12.
Рациональное число можно представитьв виде
P
Q
, где P – целое число,
Q – натуральное число.
Рациональные числа - все целые числа и все
дроби, как положительные так и отрицательные.
Рациональное выражение – алгебраическое
выражение составленное из чисел и переменных
с помощью арифметических операций и возведения
в натуральную степень.
Дробное выражение – это алгебраическая дробь.
Целое выражение - выражение представленное в
виде многочлена .
2
3.
Для преобразования рациональных выраженийпринят тот же порядок действий, что и для
преобразования числовых выражений.
Это значит, что сначала выполняют действия
в скобках, затем действия второй ступени
(умножение, деление, возведение в степень),
а затем действия первой ступени
(сложение, вычитание).
Рассмотрим наиболее сложные задания:
3
4.
Рассмотрим пример 1.Упростить выражение.
a
с
a
с
1 1
1 1
( ) : ( c a ) ca ( )
c a
c a
a c
a c
(
) : ( c a ) ca (
)
c a
c a
a c
1
a c
(
)(
) ca (
)
c a c a
c a
1
1
(a c )
a c
( a c ).
ca (
)
c a (c a )
c a 1 c a
1
1
4
5.
Рассмотрим пример 2.Упростить выражение:
a2
a3
a
a2
a )(
2
):(
2
)
2
2
a b a 2ab b
a b a b
Решение
Для упрощения выражения выбираем способ преобразования
по действиям.
a+b
1
2
3
2
3
a
a
a
a
1)
2
2
2
a b a 2ab b
a b (a b)
a (a b ) a
a a b a
a b
.
2
2
2
(a b)
(a b)
(a b)
2
3
3
2
3
2
5
6.
a-b1
2
a
a
a
a2
2)
2
2
a b a b
a b ( a b )( a b )
ab
a( a b ) a 2
a 2 ab a 2
.
( a b )( a b ) ( a b )( a b ) ( a b )( a b )
1
1
2
a 2b
ab
a b( a b )( a b )
3)
:
2
2
( a b ) ( a b )( a b )
(a b ) a b
1
1
a( a b )
a( b a )
.
(a b)
a b
6
7.
Рассмотрим пример 3.Упростить выражение:
z 2
z
z 4
2
б) 2
:(
2
2
)
4 z 16 z 16 2 z 4 2 z 8 z 2 z
2
Решение
Для упрощения выражения выбираем способ преобразования
цепочкой.
z 2
z
z 4
2
2
:(
)
2
4 z 16 z 16 2( z 2 ) 2( z 4 ) z( z 2 )
2
z 2
z
z 4
2
:(
)
2
2
4( z 4 z 4 ) 2( z 2 ) 2( z 4 ) z( z 2 )
2
7
8.
Z(Z + 2)z
2(z – 2)
z 2
z
z 4
2
:(
)
2
2
4( z 2 )
2( z 2 ) 2( z 4 ) z( z 2 )
2
z 2
z 2 ( z 2 ) z( z 2 4 ) 4( z 2 )
:(
)
2
2
4( z 2 )
2 z( z 4 )
z 2
z 3 2z 2 z 3 4z 4z 8
:(
)
2
2
4( z 2 )
2 z( z 4 )
z 2
2z 8z 8
:(
)
2
2
4( z 2 )
2 z( z 4 )
2
8
9.
z 22( z 4 z 4 )
:(
)
2
2
4( z 2 )
2 z( z 4 )
2
1
z 2
2( z 2 )
:(
)
2
2
4( z 2 ) 1 2 z( z 4 )
2
z 2
z( z 2 4 )
(
)
2
2
4( z 2 )
(z 2)
1
1
1
z
( z 2 )( z 2 )( z 2 )z
.
2
2
4( z 2 )
4( z 2 ) ( z 2 )
1
9
10.
Доказать тождество – это значит установить,что при всех допустимых значениях переменной
его левая и правая части тождественно равные
выражения.
Способы доказательства тождеств:
1) Преобразовывают левую часть и получают в итоге
правую часть;
2)Преобразовывают правую часть и получают в итоге
левую часть;
3)По отдельности преобразовывают правую, а затем
левую часть и в итоге получают равные выражения;
4) Составляют разность левой и правой части и
в итоге получают нуль.
Какой способ выбрать – зависит от конкретного
вида тождества, которое предлагают доказать.
10
11.
Рассмотрим пример 4.Доказать тождество.
y 2 10 y 25 3
y 5 3
(
) :(
) 8.
2
y 25
2 y 10
Решение
Для доказательства тождества выбираем первый способ:
преобразуем левую часть.
y 2 10 y 25 3
y 5 3
(
) :(
)
2
y 25
2 y 10
( y 5 )2
2 y 10 3
3
(
) (
)
( y 5 )( y 5 )
y 5
( y 5 )2
2( y 5 ) 3
3
(
) (
)
( y 1 5 )( y 5 )
y 5
11
12.
( y 5 ) 3 2( y 5 ) 3(
) (
)
( y 5)
y 5
3
3
( y 5 ) 8( y 5 )
3
3
( y 5) ( y 5)
1
8( y 5 ) ( y 5 )
8.
3
3
( y 5) ( y 5)
1
3
1
3
1
И так, 8 = 8.
Тождество справедливо лишь для допустимых
значений переменной у.
12





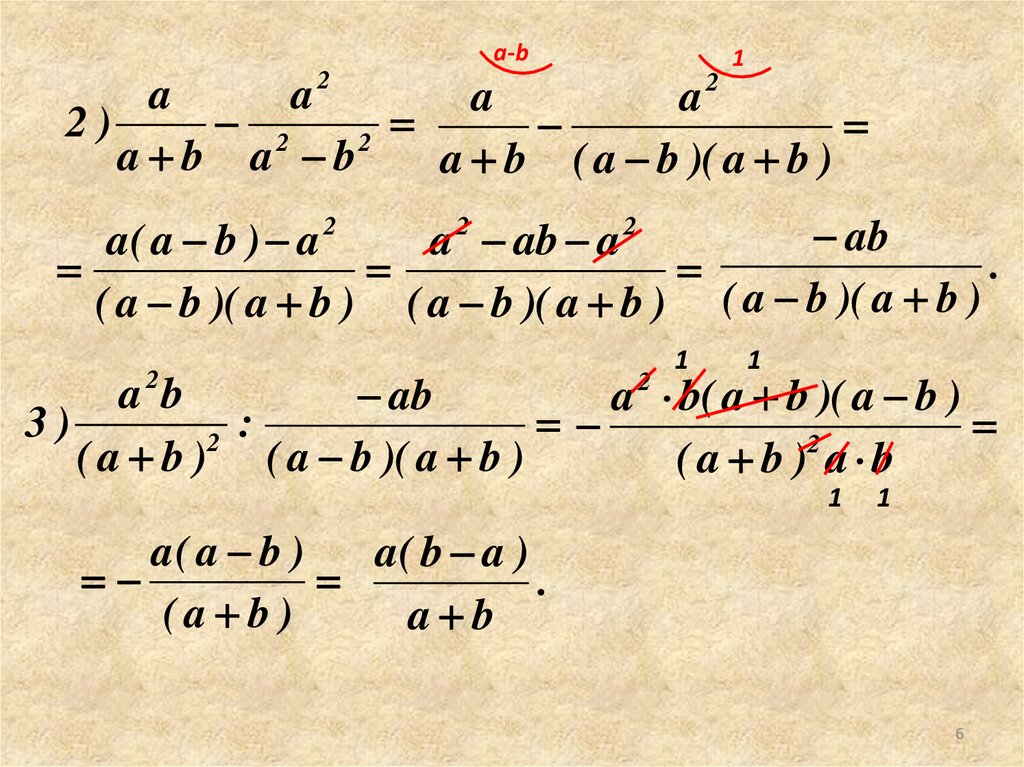

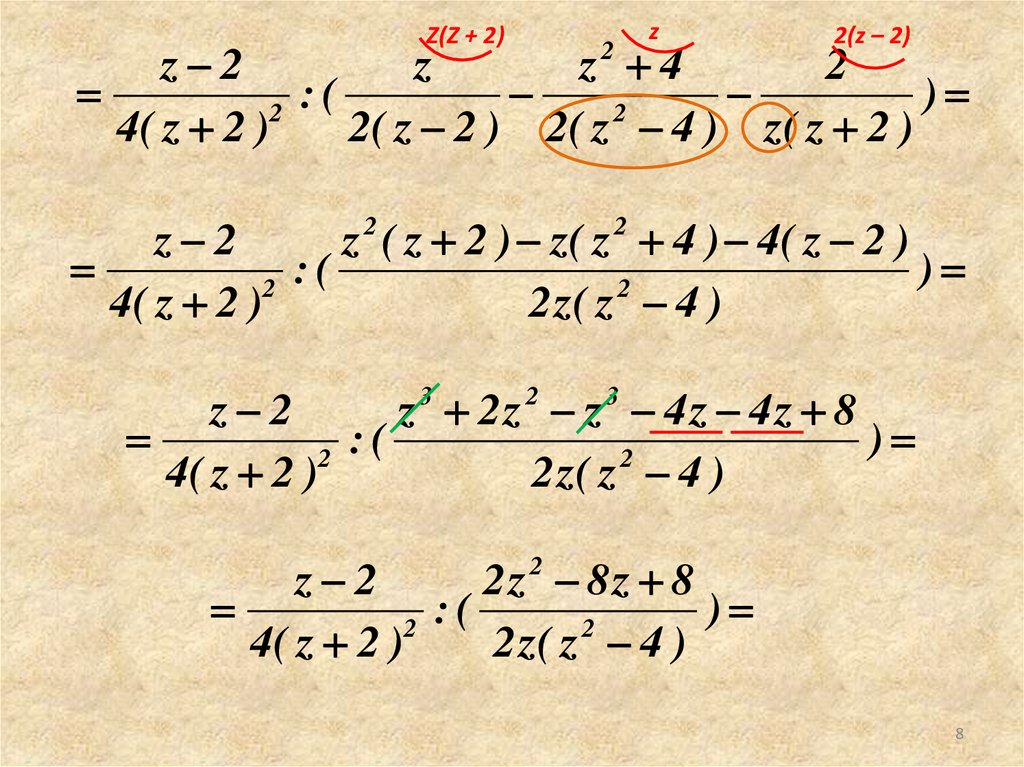
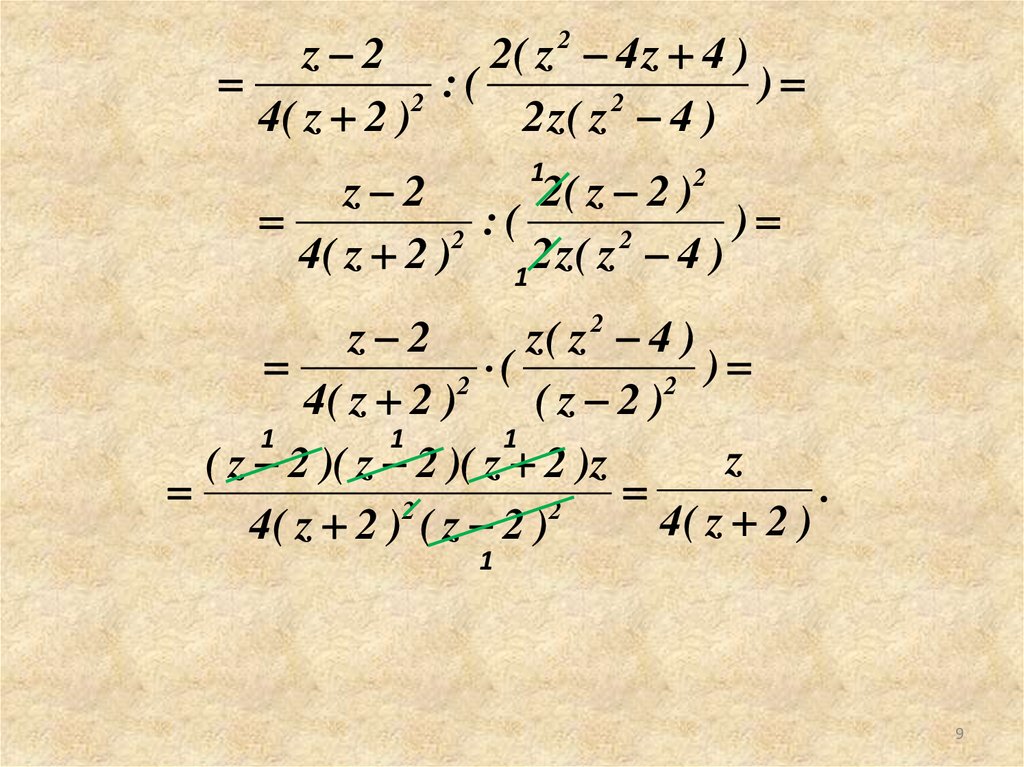



 Математика
Математика