Похожие презентации:
Алгебраические дроби
1. Краткая теория
(для изучения и повторения алгебры 7-9кл.)
2. Алгебраические дроби
1.Дроби:
многочлен1 a
многочлен 2 b
2.Оснновное свойство
3.Действия:
:
a c a c
b b
b
a c ac
b d bd
a c
a d
:
b d
bc
n
an
a
n
b
b
a 0
a
0
b
b 0
a a k a :m
k 0; m 0
b b k b : m
a c ad cb
b d
bd
3. Функция
1.функция-зависимость (соответствие) X единств.
Х-аргумент, D(f)-область определения
У- значение функции , Е(f)-область значений
2.График-множество всех точек (х;у) ,где у=f(x)
3.Способы задания
1) формула
2)график
3)таблица
4) ОПИСАНИЕ
5) СИСТЕМА УРАВНЕНИЙ
y y f x
4. Свойства функции
1.D(f)2.Е(f)
3.Точки пересечения с осями
4.Промежутки знакопостояства (f(x)>0 ,f(x)<0)
5. Промежутки возрастания (убывания)
6.Четность (f(-x)=f(x)) или нечетность (f(-x)=-f(x))
7.Периодичность (f(x+T)=f(x))
8.Экстремумы (max,min)
9.Поведение вблизи особых точек или
10.График
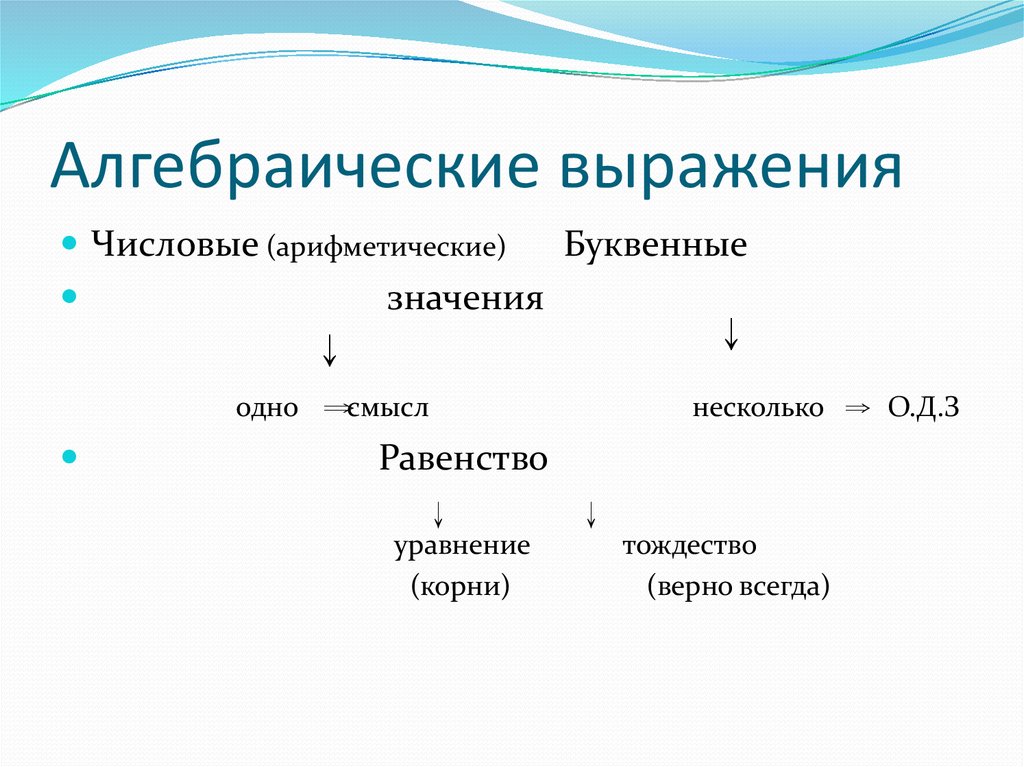
5. Алгебраические выражения
Числовые (арифметические)Буквенные
значения
одно
смысл
несколько
Равенство
уравнение
(корни)
тождество
(верно всегда)
О.Д.З
6. Многочлены
1.Одночлен -бук. часть,умн.,степ.стандартный вид: -7a 3bc 2
(-7 коэффициент) ,степень:3+1+2,
подобные:бук. части одинак.
2.Многочлен-сумма одночленов
3.Действия
(+) и (-)
2) (х) на одночлен
(х) на многочлен
3) (:) на одночлен
(:) на многочлен
1)
(стандарт. вид,степень)
раскрытие скобок
«фонтанчик»
«фонтан»
«по очереди)
3x 2 7 x 26) : ( x 2)
7. продолжение
3.Разложение на множителиа) вынесение общего множителя за скобки
б) группировка
в)применение формул сокращенного умножения
8. Формулы
a b a b a b2
a b a 2 2ab b
3
3
2
2
3
a b a 3a b 3ab b
3
3
2
2
a b a b a ab b
2
2
a b c
2
a b c 2ab 2bc 2ac
2
2
2
x 1 x 1 x x x x 1
n
a b
a b
n 1
n 2
2
1
2
1 1 2
13
3
3
3
3
3
a b a b a a b b
9. Уравнение (равенство с переменной)
1.Корень -значение переменной ,при котором равенство верноУравнения равносильны
2.Свойства
=
=
+
=
одни и те же корни или не имеют их
+a=
xa=
= -
+a
xa
-
10. Линейное уравнение
ax =bВозможные случаи:
b
1)a 0, x= a -единственный корень
2) a=0; b=0 x- число
3)a=0; b 0, - нет корня
11. Степень
ap
- степень, a-основание,p – показатель
a n a a a n раз
1)p=n
a1
2)p=1
a0 1
3)p=0
4)p=-n a n 1n a 0
a
m
5)p= n
,
m
n
a n am
12. Свойства степени
1. a p a g a p gp
g
p g
2. a : a a
3. a p g a pg
4. ab p a p b g
5.
p
ap
a
p
b
b
Стандартный вид числа
x a 10 n , n Z ,1 a 10
13. Системы уравнений
Система-это несколько уравнений , для которых надо найтиобщее решение.
Решение системы - это пара чисел , которая удовлетворяет
каждое решение.
Системы равносильны , если имеют одни и те же решения
или не имеют их.
Способы решения:
1)Графический
2) Подстановка
3) Сложение
14. Система линейных уравнений
a1 x b1 y c1a2 x b2 y c2
а) Если
a1 b1
a2 b2
,то решение одно
б) Если
a1 b1 c1
a 2 b2 c2
,то решений бесконечно много
В) Если
a1 b1 c1
a 2 b2 c2
,то решений нет
15. Неравенства
a>b ,то a-b>0a<b ,то a-b<0
a=b ,то a-b=0
Свойства:
1.a>b , то b<a (коммутативность)
2.a>b и b>c , то a>c (транзитивность)
3.a>b и c – любое , то a+ c>b+ c
4.a>b и c>0 ,то ac> b c
c<0 , то ac< b c
5.a>b>0 , то a n b n
1 1
6.a>b>0 , то
a b
16. Квадратные уравнения
Неприведенное : ax bx c 0 a 02
коэффициент , c- свободный член.
2
Приведенное : x px g 0
Неполные : ax 2 bx 0
и ax 2 c 0
Решение уравнений
1) с=0 , то ax 2 bx 0 , x ax b 0 x1 0 и
x
2) b=0 ,то ax c 0
2
,a-I коэффициент , b- II
x2
b
a
c
a
3)c 0 ,b 0 ax bx c 0
, D=b 4ac
2
b
D
4) если b на 2 , то D b ac и
2
2
4
2
x
2
4
a
и x
b D
2a
17. Существование корней
1.D>0 -два действительных корня2.D=0 –два действительных равных
3.D<0 –нет действительных корней
Теорема Виета
x 2 px g 0 , x1 x2 p и
Разложение трехчлена
x1 x2 g
ax 2 bx c a x x1 x x2
18. Квадратные корни
1. a b 0 ,где b 2 a (арифметический)2. Существует : a ,если a 0 -да ,если a<0-нет
3.
1)
2)
Свойства:
ab a b
a
b
a
b
3) a 2 a
4) a 2 b a b
5) a b a b , 6)
2
a
2
a
19. Действительные числа
СоставN= 1,2,3, ,
Z= , , 2, 1,0,1,2,
G=Z дроби рациональные
J- иррациональные
R=G J
Возможный вид
n
m
m
или беск.период.дес.др.
n
беск.непериод.десят.др.
всякие десят.др.
20. Корни натуральной степени
1.2.
n
a b bn a
n
a 0-арифметический
3.Существует: n=2k для a 0, n a
4.
1)
3)
5)
,n=2k+1 для всех a,но один!
Свойства
n
ab a b
n
n k
a
2k
2k
a
n
nk
a
a
a
b
2) n
4)nk
6)
a
n
b
a mk n a m
a
n
n
n
a
21. Арифметическая прогрессия
1.a
an 1 an d
2. Формула n-го члена :
3. Сумма : S a1 an n
an a1 d n 1
2a1 d n 1
или
S
n
2
n
4. Свойства
2) d an 1 an
1) an
an am
n m
an 1 an 1
2
(среднее арифметическое)
22. Геометрическая прогрессия
bn1.
bn 1 bn g g 0иg 1
2. Формула n-го члена :
b g b1
Sn n
g 1
3. Сумма :
bn b1 g n 1
или
b1 g n 1
Sn
g 1
4.Свойства :
bn 1
bn
n m
g
1)
bn
bm
2) bn
bn 1 bn 1
(среднее геометрическое)
23. Бесконечно убывающая прогрессия
1.2.
g 1
3. Сумма :
b1
S
1 g
S lim S n приn






















 Математика
Математика