Похожие презентации:
Синус, косинус, тангенс угла. 9 класс
1. Синус, косинус, тангенс угла.
9 класс.2.
Единичная полуокружностьРассмотрим ∆ОДМ
МД
ОД
sin
, cos
У
ОМ
ОМ
sin α = у
С(0;1)
h
cos α = х
М(х;у)
α
В(-1;0)
О
Д
А(1;0)
Х
ОМ=1, МД=У, ОД=Х отсюда sinα=? cos α=?
3.
sin ордината у точки М ,cos абсцисса х точки М
У
cos0°= 1
sin0°= 0
sin90°=1
sin180°=0
cos90°= 0
cos180°=-1
М(х;у)
α
Д
О
Х
0 у 1, 1 х 1, то для любого 0≤sinα≤1
из промежутка 0 180
-1≤ cosα≤1
4.
Основное тригонометрическое тождествох у 1
2
2
sin х,
cos у
-уравнение окружности R=1, О(0;0)
sin сos 1
2
2
5.
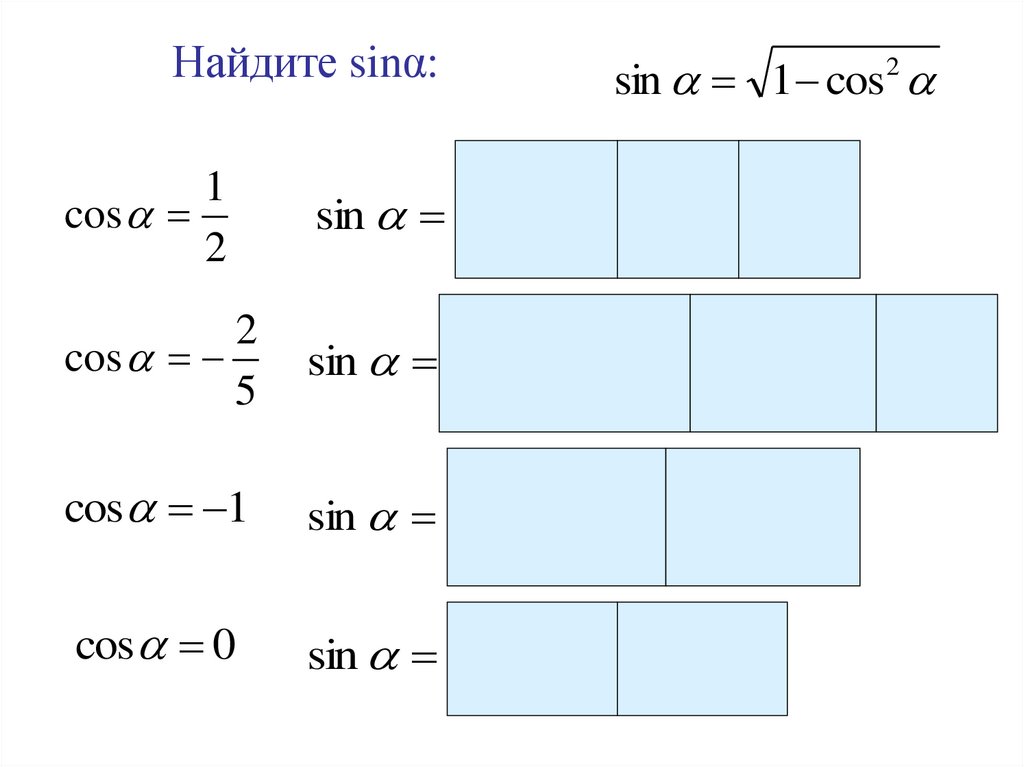
Найдите sinα:sin 1 cos2
1
cos
2
1
sin 1
4
2
cos
5
2 2
4
21
sin 1 ( ) 1
5
25
5
cos 1
sin 1 ( 1) 1 1 0
cos 0
sin 1 02 1 1
3
3
4
2
2
6.
Найдите cosα:cos 1 sin 2
3
sin
2
3
cos 1
4
1
1
4
2
1
sin
4
1
15
15
cos 1
16
16
4
sin 1
cos 1 12 0
7.
sintg
cos
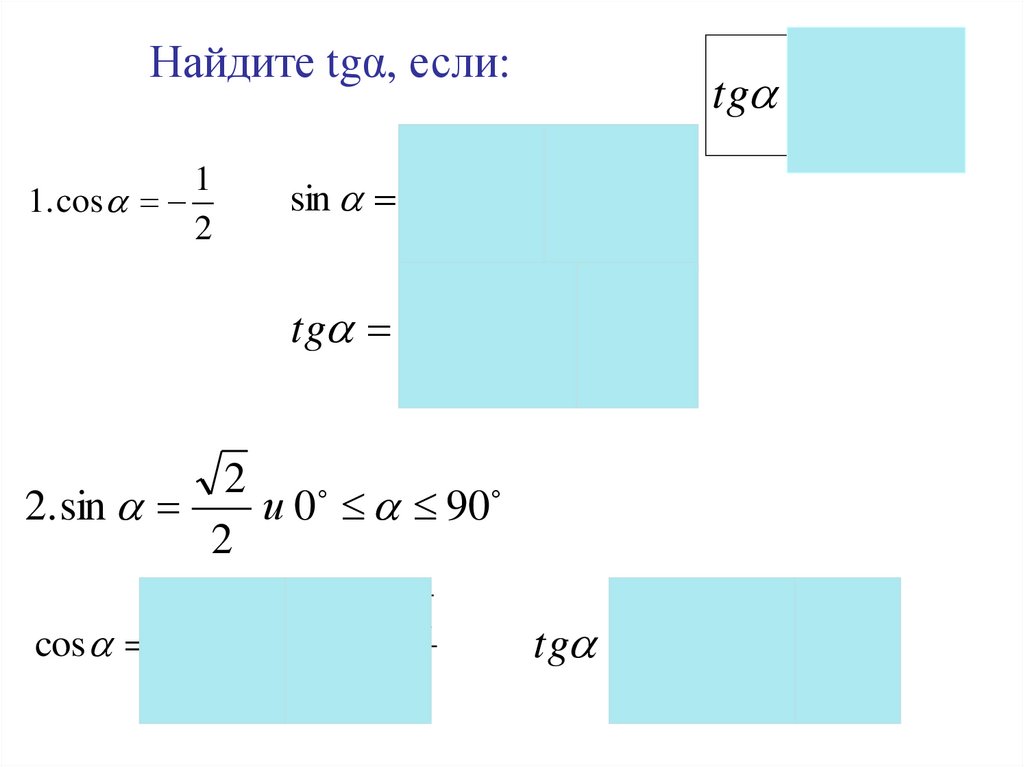
Найдите tgα, если:
1
1. cos
2
1
3
3
sin 1
4
4
2
3
1
tg
: ( ) 3
2
2
2
2. sin
и 0 90
2
2
2
2
cos 1
4
4
2
2
2
tg
:
1
2
2
8.
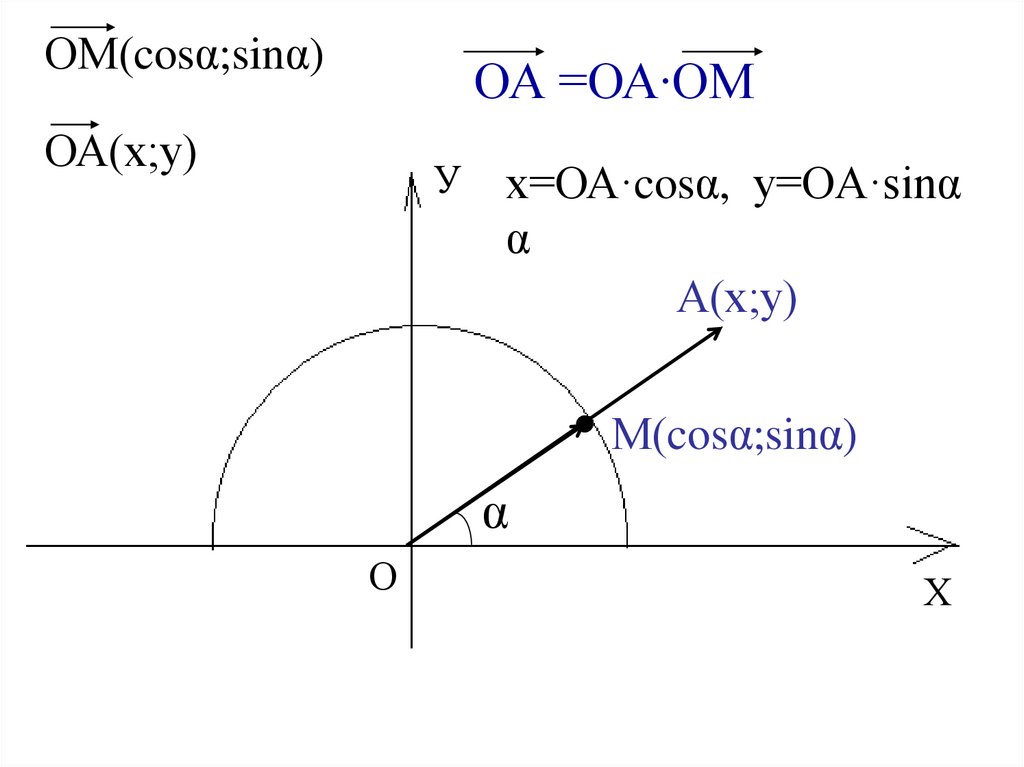
ОМ(cosα;sinα)ОА =ОА∙ОМ
ОА(х;у)
У
х=ОА·cosα, у=OA·sinα
α
А(х;у)
М(cosα;sinα)
α
О
Х





 Математика
Математика








