Преобразование фигур на плоскости. Виды движения

1.

Геометрия.
Преобразование фигур на плоскости.
Виды движения.

2.

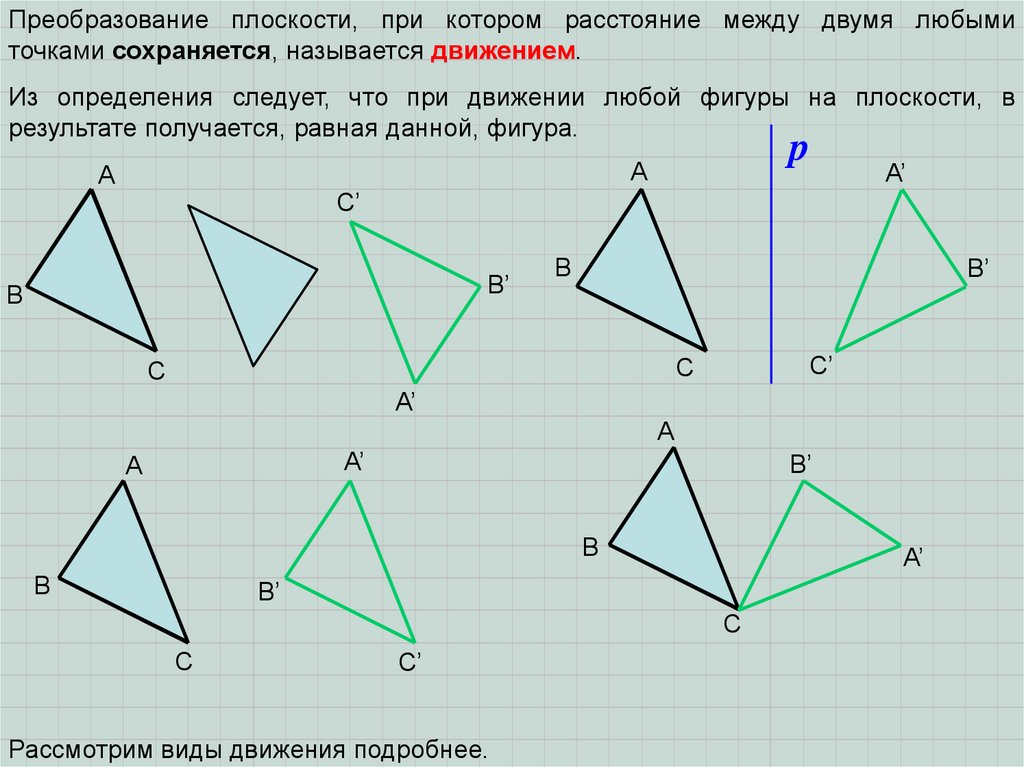
Преобразование плоскости, при котором расстояние между двумя любыми
точками сохраняется, называется движением.
Из определения следует, что при движении любой фигуры на плоскости, в
результате получается, равная данной, фигура.
p
A
A
A’
C’
O
B’
B
B’
B
C’
C
C
A’
A
A’
A
B’
B
B
A’
B’
C
C
C’
Рассмотрим виды движения подробнее.

3.

4.

5.

6.

7.

8.

9.

10.

Центральная симметрия(симметрия
относительно точки).
Две точки Х и Х’ являются симметричными относительно точки О, если:
1) О ХХ’ (т.е. все три точки принадлежат одной прямой);
2) ОХ=ОХ’.
Х
О
Х’
Точка О является центром симметрии.

11.

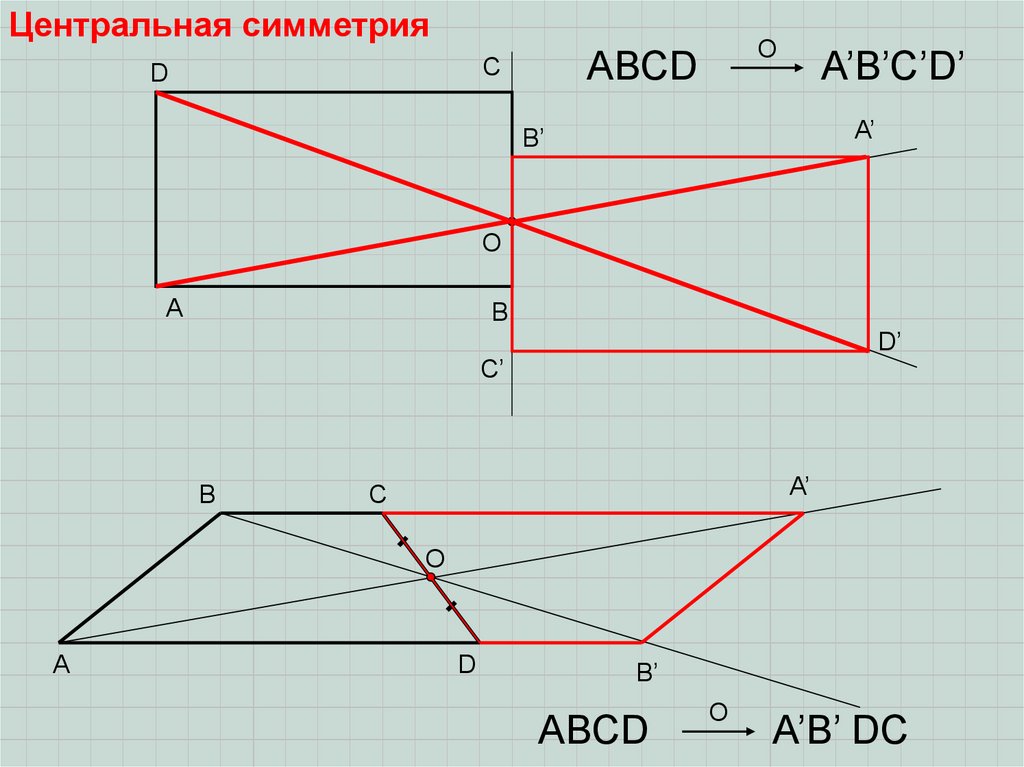
Центральная симметрия
D
O
ABCD
C
A’B’C’D’
A’
B’
O
A
B
D’
C’
B
A’
C
O
A
D
B’
ABCD
O
A’B’ DC

12.

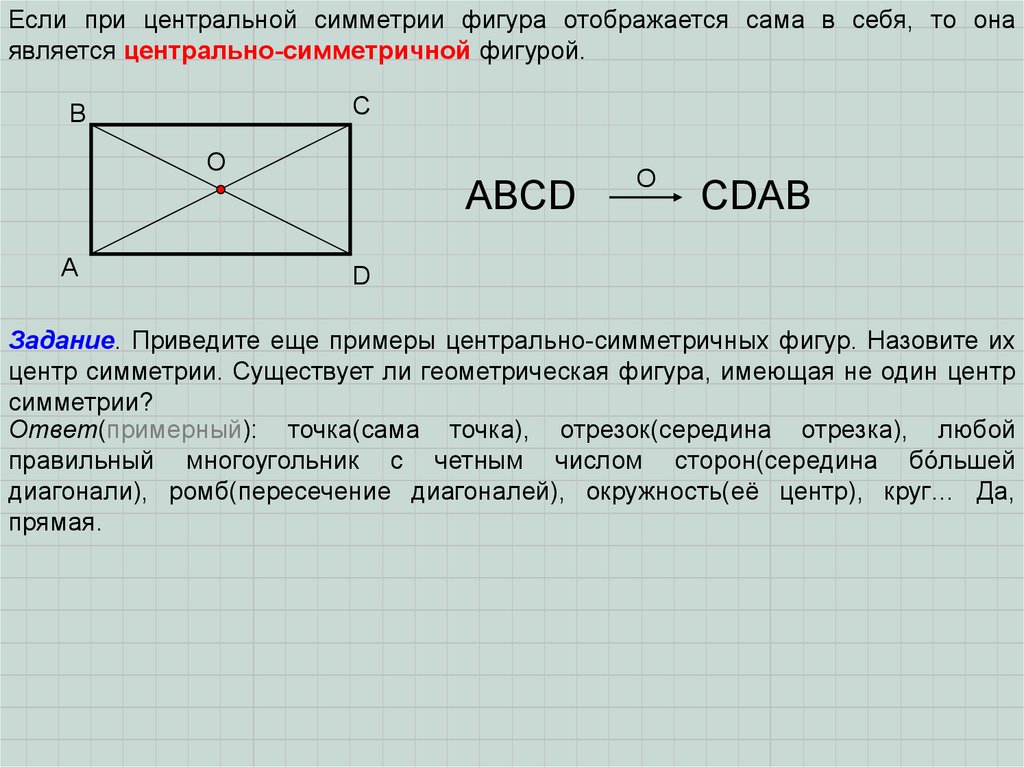
Если при центральной симметрии фигура отображается сама в себя, то она
является центрально-симметричной фигурой.
C
B
O
ABCD
A
O
СDAB
D
Задание. Приведите еще примеры центрально-симметричных фигур. Назовите их
центр симметрии. Существует ли геометрическая фигура, имеющая не один центр
симметрии?
Ответ(примерный): точка(сама точка), отрезок(середина отрезка), любой
правильный многоугольник с четным числом сторон(середина бóльшей
диагонали), ромб(пересечение диагоналей), окружность(её центр), круг… Да,
прямая.

13.

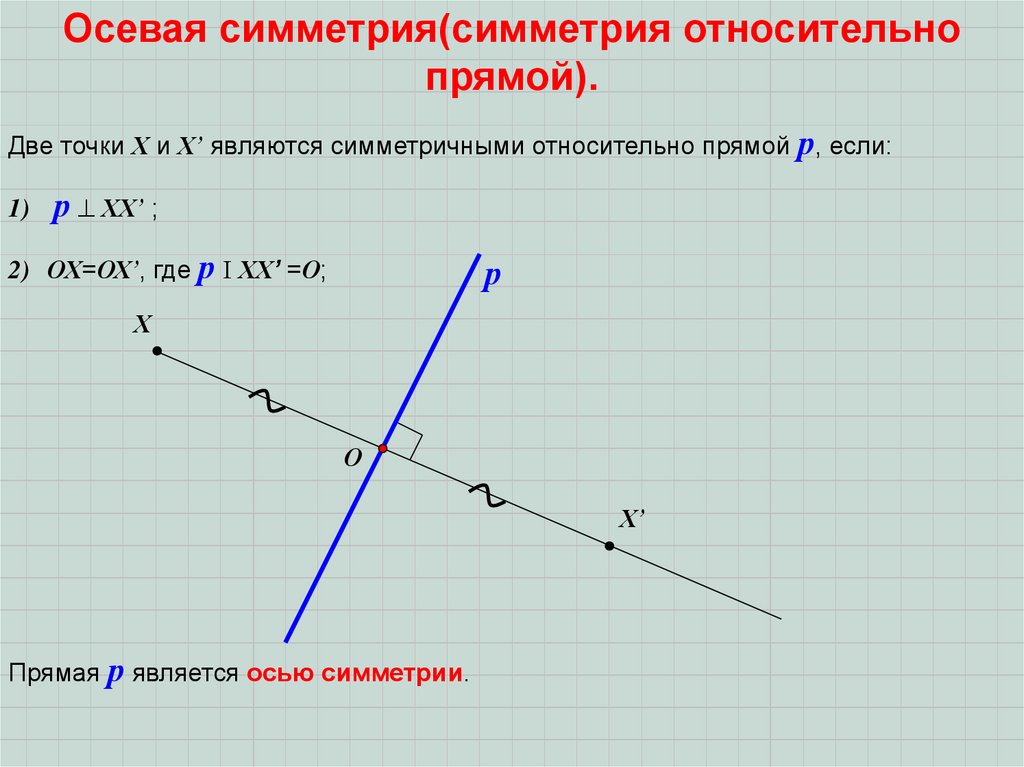
Осевая симметрия(симметрия относительно
прямой).
Две точки Х и Х’ являются симметричными относительно прямой р, если:
1)
р ХХ’ ;
2) ОХ=ОХ’, где р ХХ’ =О;
р
Х
О
Х’
Прямая р является осью симметрии.

14.

B
Осевая симметрия
C
ABCD
A
CD
A’B’CD
D
B’
A’
m
B’
B
C’
A
D
A’
C
D’
ABCD
m
A’B’C’D’

15.

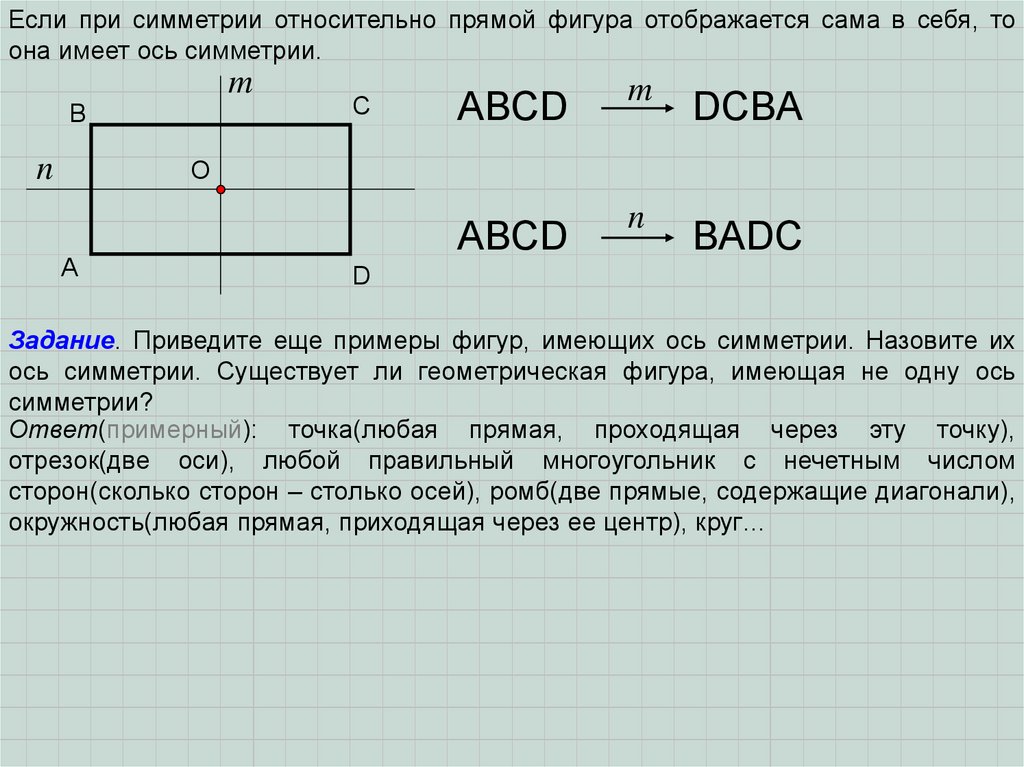
Если при симметрии относительно прямой фигура отображается сама в себя, то
она имеет ось симметрии.
m
B
n
C
ABCD
m
DСBA
ABCD
n
BADС
O
A
D
Задание. Приведите еще примеры фигур, имеющих ось симметрии. Назовите их
ось симметрии. Существует ли геометрическая фигура, имеющая не одну ось
симметрии?
Ответ(примерный): точка(любая прямая, проходящая через эту точку),
отрезок(две оси), любой правильный многоугольник с нечетным числом
сторон(сколько сторон – столько осей), ромб(две прямые, содержащие диагонали),
окружность(любая прямая, приходящая через ее центр), круг…

16.

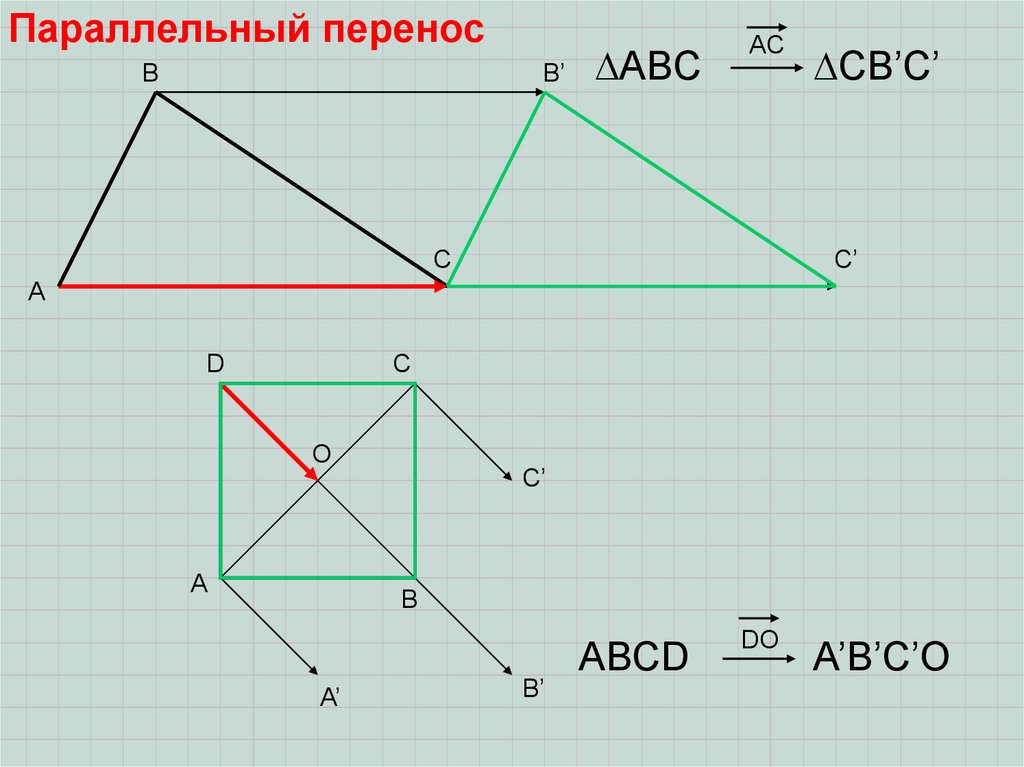
Параллельный перенос
При этом преобразовании плоскости все точки фигуры перемещаются в одном
направлении на одно и то же расстояние. Естественно задавать его с помощью
вектора.
Х’
Х
a
Точка Х’ является образом точки Х при параллельном переносе на a, если:
XX ' a
Очевидно, что фигура отобразится сама в себя при параллельном переносе на 0
(нулевой вектор).

17.

Параллельный перенос
B’
B
ABC
AC
CB’C’
C’
C
A
D
C
O
A
C’
B
A’
B’
ABCD
DO
A’B’C’O

18.

Поворот
Чтобы выполнить поворот фигуры необходимо задать: 1) центр поворота, 2)
направление поворота и 3) величину угла поворота. Второе и третье условия
можно объединить, оговорив, что отрицательные углы откладываются в
направлении «по часовой стрелке», а положительные – против.
Х’
О – центр поворота
Х
О
Точка Х’ является образом точки Х при повороте около точки О на угол , если:
1) ХО=Х’O;
2) XOX’= .

19.

Пример поворота правильного шестиугольника ABCDEF вокруг точки D на прямой
угол по часовой стрелке.
A’
F’
B
B’
C
C’
E’
A
D
F
E
ABCDEF
-900
D
A’B’C’DE’F’