Интерполяция функций

1.

Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ижевский государственный технический университет
имени М. Т. Калашникова»
Кафедра «АСОИУ»
Курс «Вычислительная математика»
Тема «Интерполяция функций»
Автор Исенбаева Е.Н., старший преподаватель
Ижевск
2013

2. Аппроксимация функций

Аппроксимация- подмена одной
функции f(x) другой функцией
φ(x), близкой к f(x) и обладающей
«хорошими» свойствами,
позволяющими легко производить
над нею аналитические или
вычислительные операции.
Курс «Вычислительная математика»
Тема «Интерполяция функций»
2

3. Аппроксимация функций

Задача аппроксимации:
f (x) ≈ φ (x) (1)
Курс «Вычислительная математика»
Тема «Интерполяция функций»
3

4. Полиномиальная аппроксимация

• φ (x)– многочлен или
функция, состоящая из
многочленов→полиномиальн
ая аппроксимация или
кусочно-полиномиальная
аппроксимация.
Курс «Вычислительная математика»
Тема «Интерполяция функций»
4

5. Полиномиальная аппроксимация

• Y=f(x)- функция, заданная
таблицей(сеткой)
значений.
Курс «Вычислительная математика»
Тема «Интерполяция функций»
5

6. Интерполяционный многочлен Лагранжа

• В точках x0, x1,…,xn таких, что a ≤
x0 ≤…≤ xn ≤ b, известны значения
функции y=f(x)→ на [a,b] задана
табличная (сеточная) функция
f(x):
(x0,y0);(x1,y1);(x2,y2)…(xn,yn) (2)
Курс «Вычислительная математика»
Тема «Интерполяция функций»
6

7. Интерполяционный многочлен Лагранжа

• Значения φ (x0), φ (x1),…, φ (xn) в
узлах интерполяции x0,…,xn
совпадают с заданными
значениями f (x), т.е. с y0, y1,
y2,…,yn→ функция φ (x)
интерполирующая
(интерполяционная) для f (x) на
[a,b].
Курс «Вычислительная математика»
Тема «Интерполяция функций»
7

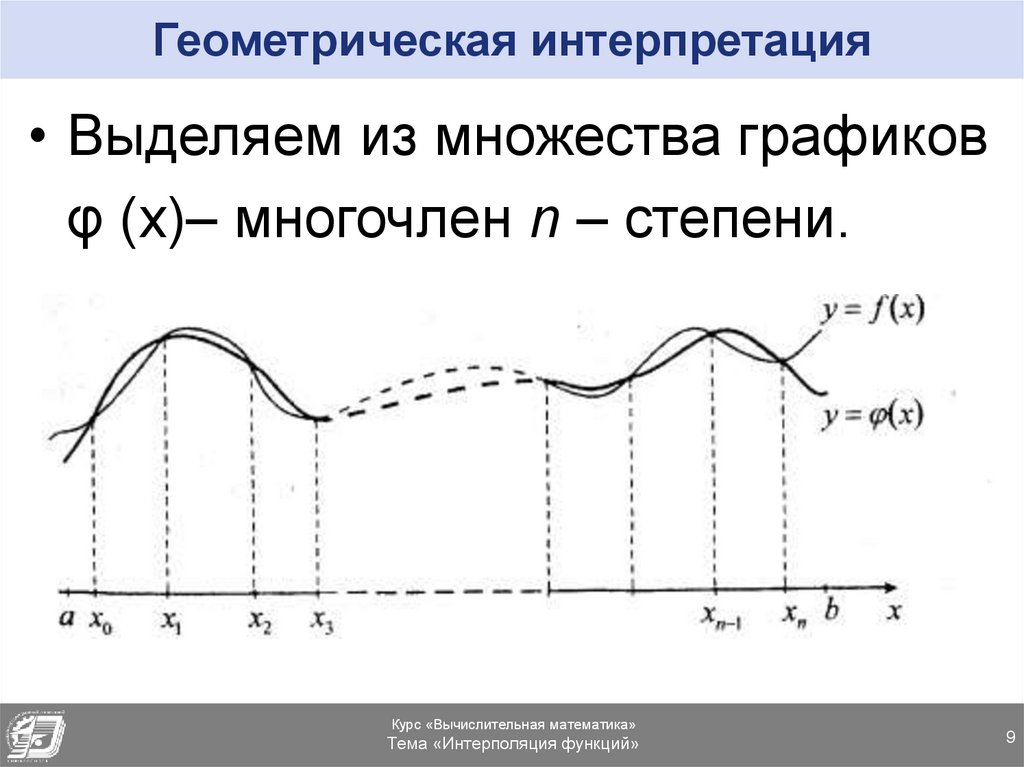
8. Геометрическая интерпретация

• График φ (x) проходит так,
что, по меньшей мере, в (n+1)
заданных точках он
пересекает или касается
графика f (x).
Курс «Вычислительная математика»
Тема «Интерполяция функций»
8

9. Геометрическая интерпретация

• Выделяем из множества графиков
φ (x)– многочлен n – степени.
Курс «Вычислительная математика»
Тема «Интерполяция функций»
9

10. Математическая постановка задачи

Для функции f (x) заданной
таблично (2) найти многочлен
Pn(x) такой, что выполняется
совокупность условий
интерполяции:
Pn(xi) = yi
iͼ{0,1,…,n} (3)
Курс «Вычислительная математика»
Тема «Интерполяция функций»
10

11. Интерполяционный многочлен Лагранжа

Построим многочлен n степени Ln(x) в
виде линейной комбинации многочленов n
же степени li(x) (i=0,1,…,n),
где i- не степень, а номер многочлена,
Курс «Вычислительная математика»
Тема «Интерполяция функций»
11

12. Интерполяционный многочлен Лагранжа

ci=y=f(xi)
Курс «Вычислительная математика»
Тема «Интерполяция функций»
12

13. Интерполяционный многочлен Лагранжа

Базисный многочлен Лагранжа
Курс «Вычислительная математика»
Тема «Интерполяция функций»
13

14. Интерполяционный многочлен Лагранжа

Искомый интерполяционный
многочлен Лагранжа:
Курс «Вычислительная математика»
Тема «Интерполяция функций»
14

15. Построение многочленов Лагранжа

•Записать
интерполяционный
многочлен Лагранжа
первой и второй
степени.
Курс «Вычислительная математика»
Тема «Интерполяция функций»
15

16. Построение многочленов Лагранжа

• По 2 точкам (х0,у0); (х1,у1)многочлен 1 степени:
Курс «Вычислительная математика»
Тема «Интерполяция функций»
16

17. Построение многочленов Лагранжа

• По 3 точкам (х0,у0); (х1,у1);
(х2,у2);- - многочлен 2 степени:
Курс «Вычислительная математика»
Тема «Интерполяция функций»
17

18. Пример построения многочлена Лагранжа

Курс «Вычислительная математика»
Тема «Интерполяция функций»
18

19. Пример построения многочлена Лагранжа

Курс «Вычислительная математика»
Тема «Интерполяция функций»
19

20. Интерполяция и экстраполяция

• Интерполяция- нахождение
промежуточных значений
функции внутри таблицы в
пределах промежутка [x0,xn].
Курс «Вычислительная математика»
Тема «Интерполяция функций»
20

21. Интерполяция и экстраполяция

• Экстраполяция- нахождение
приближенных значений
функции за пределами
промежутка [x0,xn].
Курс «Вычислительная математика»
Тема «Интерполяция функций»
21

22. Оценка погрешности интерполяционной формулы Лагранжа

Остаточный член интерполяционной формулы Лагранжа:
-(n+1)-производная функции
Курс «Вычислительная математика»
Тема «Интерполяция функций»
22

23. Недостатки интерполяционного многочлена Лагранжа

1.Громоздкость
большие
вычислительные
затраты
Курс «Вычислительная математика»
Тема «Интерполяция функций»
23

24. Недостатки интерполяционного многочлена Лагранжа

2. Неизвестна степень
многочлена, которую нужно
построить для
интерполирования функции с
требуемой точностью
Курс «Вычислительная математика»
Тема «Интерполяция функций»
24

25. Недостатки интерполяционного многочлена Лагранжа

3. Многочлен (n-1)-степени
плохо перестраивается в
многочлен n- степени
Курс «Вычислительная математика»
Тема «Интерполяция функций»
25

26. Недостатки интерполяционного многочлена Лагранжа

4. Погрешности входных
данных & большие значения n
нарушается сходимость
многочлена Лагранжа к f(х)
Курс «Вычислительная математика»
Тема «Интерполяция функций»
26

27. Интерполяционная схема Эйткена

• Интерполяционная схема Эйткенавычислительная схема получения
приближенного значения сетевой функции
f(x) в заданной точке на основе
лагранжевой интерполяции, имеющая
итерационный характер.
Курс «Вычислительная математика»
Тема «Интерполяция функций»
27

28. Вывод интерполяционной формулы схемы Эйткена

По двум точкам на y=f(x): (x0,y0); (x1,y1)
Введем функцию через определитель:
Курс «Вычислительная математика»
Тема «Интерполяция функций»
28

29. Вывод интерполяционной формулы схемы Эйткена

По двум точкам на y=f(x): (x1,y1); (x2,y2)
Введем функцию через определитель:
Курс «Вычислительная математика»
Тема «Интерполяция функций»
29

30. Вывод интерполяционной формулы схемы Эйткена

По трем точкам на y=f(x): (х0,у0);
(x1,y1); (x2,y2)
Введем функцию через определитель
Курс «Вычислительная математика»
Тема «Интерполяция функций»
30

31. Вывод интерполяционной формулы схемы Эйткена

Курс «Вычислительная математика»
Тема «Интерполяция функций»
31

32. Вывод интерполяционной формулы схемы Эйткена

Курс «Вычислительная математика»
Тема «Интерполяция функций»
32

33. Рекуррентная интерполяционная формула схемы Эйткена

Курс «Вычислительная математика»
Тема «Интерполяция функций»
33

34. Условие выхода из итерационного процесса

уменьшается
→уточняется приближенное значение f(х҃)
→ итерационный процесс продолжаем.
Иначе - выход из итерационного процесса
• Номер i подбирается близким к х҃.
Курс «Вычислительная математика»
Тема «Интерполяция функций»
34

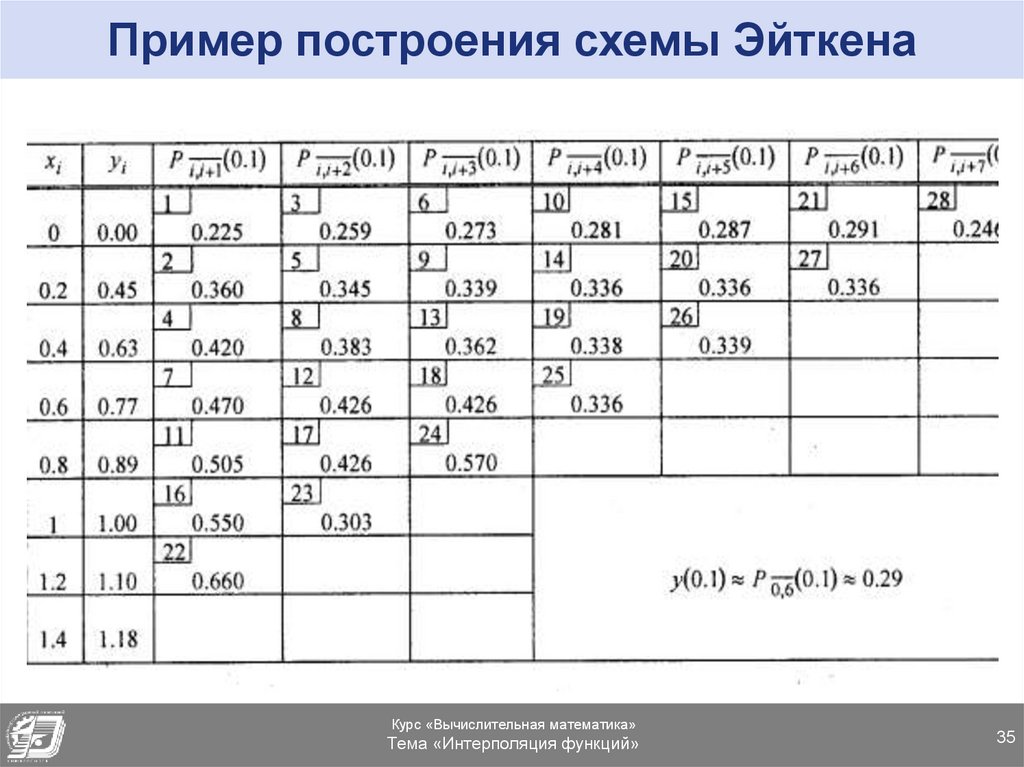
35. Пример построения схемы Эйткена

Курс «Вычислительная математика»
Тема «Интерполяция функций»
35

36.

СПАСИБО ЗА ВНИМАНИЕ
© ФГБОУ ВПО ИжГТУ имени М.Т. Калашникова, 2013
© Исенбаева Елена Насимьяновна, 2013