Похожие презентации:
Интерполирование функций. Интерполяционный многочлен Лагранжа
1. ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
Интерполяционный многочленЛагранжа
2. Постановка задачи аппроксимации функций
В основе многих численных методов лежит замена однойфункции f(x) другой функцией (x), близкой к f(x) и
обладающей «хорошими» свойствами, позволяющими
легко производить над нею аналитические или
вычислительные операции. Такая замена называется
аппроксимацией или приближением функции f(x)
функцией (x).
Поводом для аппроксимации функции может послужить, в
частности, табличный способ ее задания. Такое задание
функции встречается, например, когда значения
функции, представляющей собой некоторую физическую
величину, получаются из опыта (в дискретные моменты
времени снимаются показания приборов), а
аналитическое выражение функции неизвестно.
3.
Предположим, что в результате некоторогоэксперимента для конечного набора значений хi
величины х из отрезка [a, b]
a = х0< х1<…< хi<…< хn = b
получен набор значений yi величины y. Если допустить,
что между х и y существует функциональная
зависимость y=f(x), можно поставить вопрос о поиске
аналитического представления функции f . Очевидно,
что в такой общей постановке эта задача решается
неоднозначно. Точки х0, х1, …, хn в этом случае
называются узлами. Если расстояние h=хi+1–хi
является постоянным (независящим от i), то сетка
значений называется равномерной.
Повод для аппроксимации может возникнуть даже
тогда, когда аналитическое выражение для
некоторой функции y=f(x) известно, но малопригодно
для вычислений.
4.
В этих случаях применяется следующий прием – поисходной информации (таблица значений функции
f(x)) строится приближенная функция φ(x), которая в
некотором смысле близка к функции f(x) и
аналитическим выражением которой можно
воспользоваться для вычисления приближенного
значения f(x), считая, что
f(x) ≈φ(x).
Чаще всего задача аппроксимации решается с
помощью многочленов. Вычисления значений
многочленов легко автоматизировать, легко
вычисляются производная и интеграл от многочлена.
Наряду с многочленами используются ряды Фурье,
экспоненциальные, логарифмические и другие
элементарные функции.
5. Постановка задачи интерполирования функции
Пусть некоторая функция f(x) задана таблично наотрезке [a, b].
x
a = x0
x1
…
b = xn
f(x)
y0
y1
…
yn
Классический подход к решению задачи построения
приближающей функции φ(x) основывается на
требовании строгого совпадения значений f(x) и φ(x) в
точках хi, (i = 0, 1, 2,..., n):
f(xi) = φ(xi), i = 0, 1, 2, ... , n
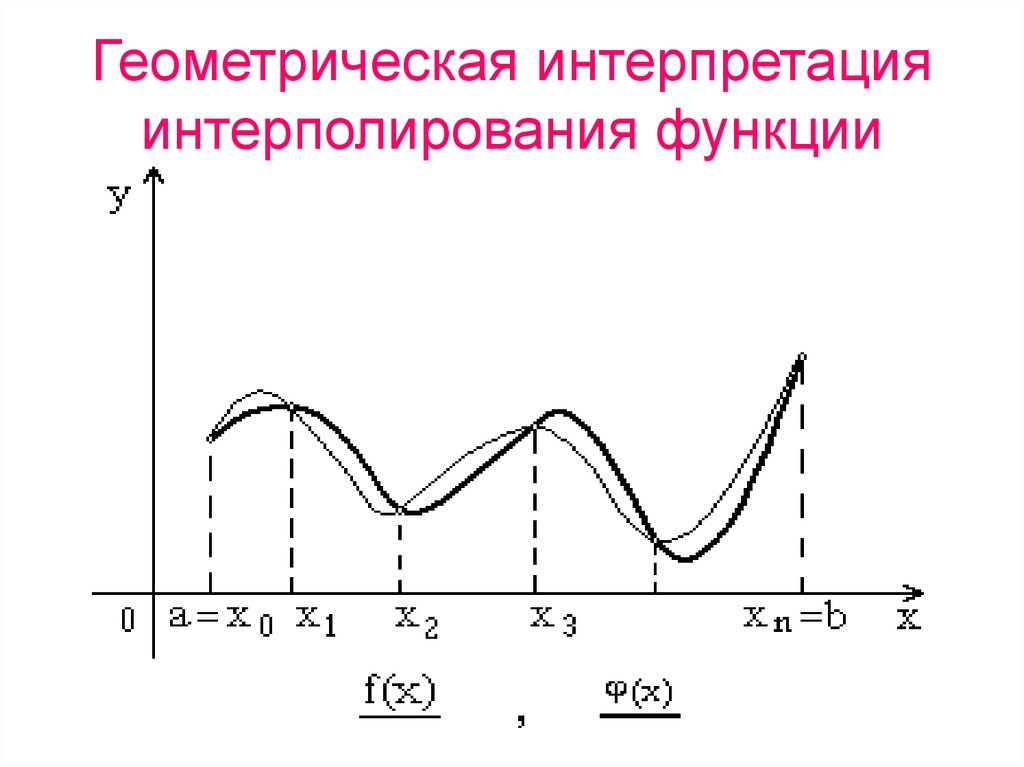
Нахождение приближенной функции называют
интерполяцией (или интерполированием), а точки
x0, x1, ... , xn – узлами интерполяции.
6.
Полученную интерполяционную формулу φ(x)обычно используют для приближенного
вычисления значений данной функции f(x) для
значения аргумента х, отличных от узлов
интерполирования. Такая операция
называется интерполированием функции f(x).
При этом различают интерполирование в
узком смысле, когда x x0 , xn
т.е. значение х является промежуточным между
х0 и хn , и экстраполирование, когда x x0 , xn
7. Геометрическая интерпретация интерполирования функции
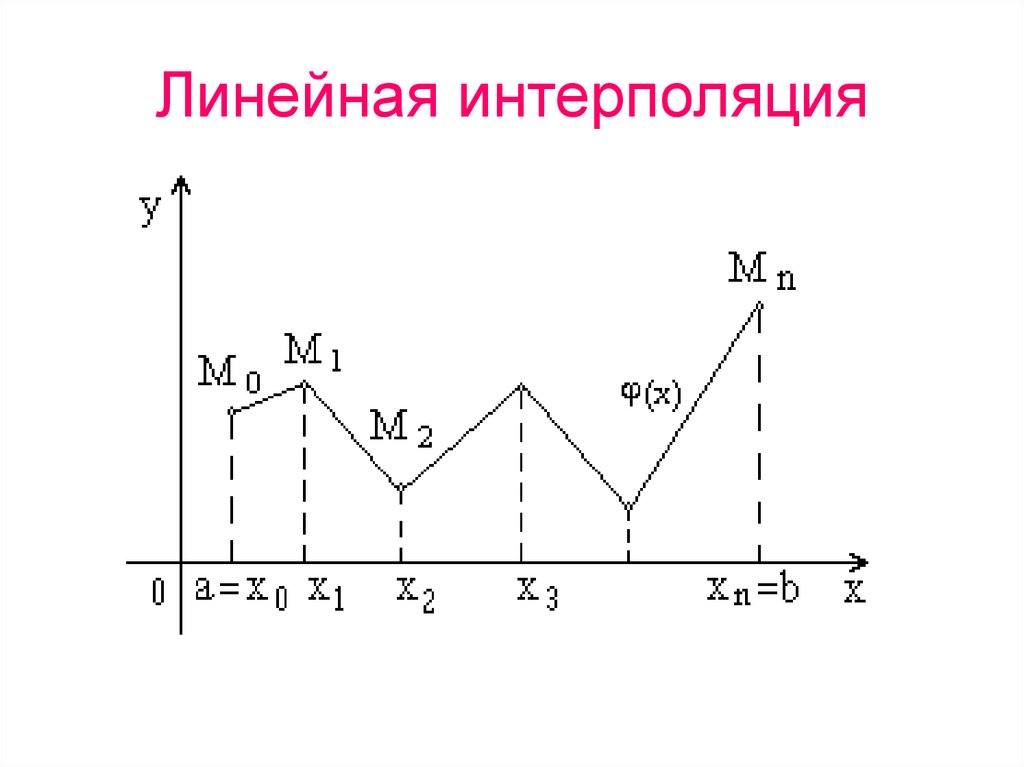
8. Линейная интерполяция
9. Интерполяционный многочлен Лагранжа
часто ищут интерполирующую функцию в видемногочлена степени n:
( x) n ( x) c0 c1 x ... cn 1 x n 1 cn x n
В постановке задачи требуется совпадение φ(xi)=уi . Из
условия Рn(xi)= уi , i=0, 1, 2, ... , n , получим
следующую систему уравнений:
c0 c1 x0 ... cn x0 n y0
n
c0 c1 x1 ... cn x1 y1
....................................
c c x ... c x n y
n n
n
0 1 n
Мы имеем систему n+1 уравнений с n+1
неизвестными c0, c1, ... , cn.
10.
Решив данную систему и разложив многочленпо корням, получим интерполяционный
многочлен Лагранжа:
n
n ( x) yi
i 0
n
(x x j )
j 0, j i
( xi x j )
f ( x) n ( x)
11. Пример 1. Построить интерполяционный многочлен Лагранжа для функции , заданной таблично:
i xi yi2
2 ( x) yi
i 0
2
(x x j )
j 0, j i
( xi x j )
0
1
2
1 12
3 4
4 6
( x x0 )( x x2 )
( x x0 )( x x1 )
( x x1 )( x x2 )
2 ( x) y0
y1
y2
( x0 x1 )( x0 x2 )
( x1 x0 )( x1 x2 )
( x2 x0 )( x2 x1 )
( x 3)( x 4) ( x 1)( x 4) ( x 1)( x 3)
2 ( x) 12
4
6
(1 3)(1 4)
(3 1)(3 4) (4 1)( 4 3)
2( x 2 7 x 12) 2( x 2 5 x 4) 2( x 2 4 x 3) 2 x 2 12 x 22
2 ( x) 2 x 2 12 x 22
12. Оценка погрешности интерполяционной формулы Лагранжа
Пусть для функции у=f(x) построен нтерполяционный многочлен Лагранжа Рn(x), принимающий вточках x0, x1, ... , xn заданные значения
y0 f ( x0 ), y1 f ( x1 ),..., yn f ( xn ).
Возникает вопрос, насколько близко построенный
полином приближается к функции f(x) в других
точках, т.е. как велик остаточный член
Rn ( x) f ( x) n ( x).
13.
Обозначив черезM n 1 max f ( n 1) ( x)
a x b
получим следующую оценку для абсолютной
погрешности интерполяционной формулы Лагранжа:
M n 1
Rn ( x) f ( x) n ( x)
n 1 ( x ) ,
(n 1)!
где
n 1
( x) ( x x0 )( x x1 )...( x xn ).











 Математика
Математика








