Похожие презентации:
Волновые процессы
1.
«ВОЛНОВЫЕ ПРОЦЕССЫ»Упругие волны
распространение упругих колебаний;
волна;
параметры и уравнения волны;
дисперсия волн;
энергия упругой волны;
отражение упругих волн;
интерференция и дифракция упругих волн
стоячие волны;
звуковые волны;
эффект Доплера
Электромагнитные волны
свет – электромагнитная волна;
2.
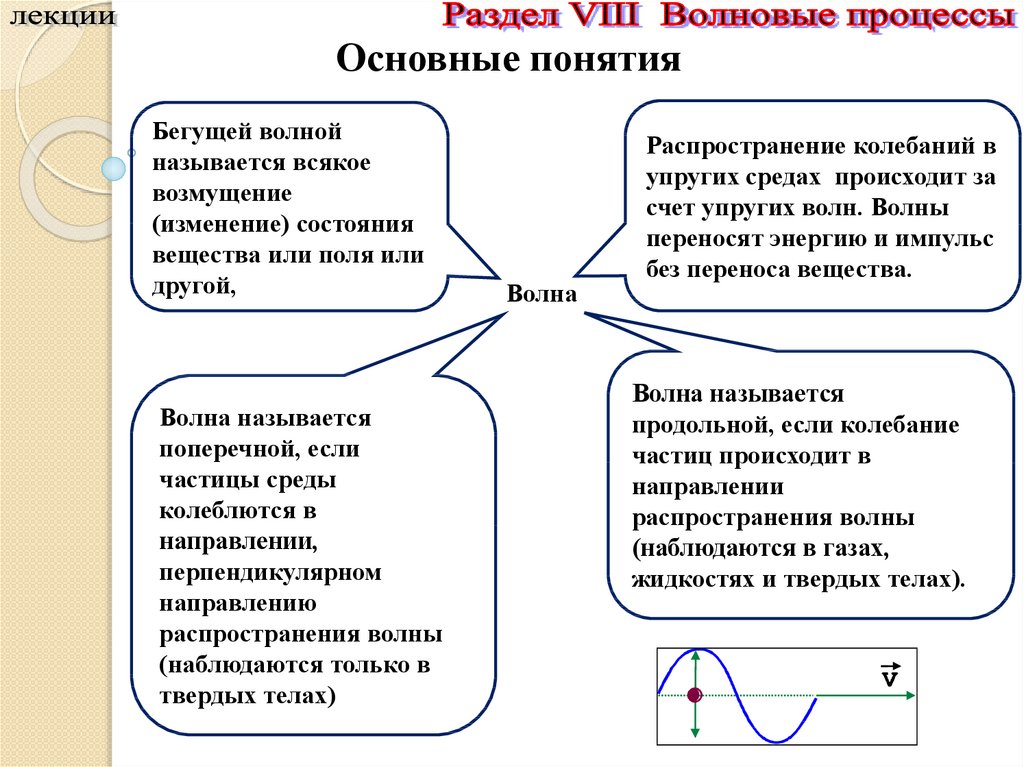
Основные понятияБегущей волной
называется всякое
возмущение
(изменение) состояния
вещества или поля или
другой,
Волна называется
поперечной, если
частицы среды
колеблются в
направлении,
перпендикулярном
направлению
распространения волны
(наблюдаются только в
твердых телах)
Волна
Распространение колебаний в
упругих средах происходит за
счет упругих волн. Волны
переносят энергию и импульс
без переноса вещества.
Волна называется
продольной, если колебание
частиц происходит в
направлении
распространения волны
(наблюдаются в газах,
жидкостях и твердых телах).
3.
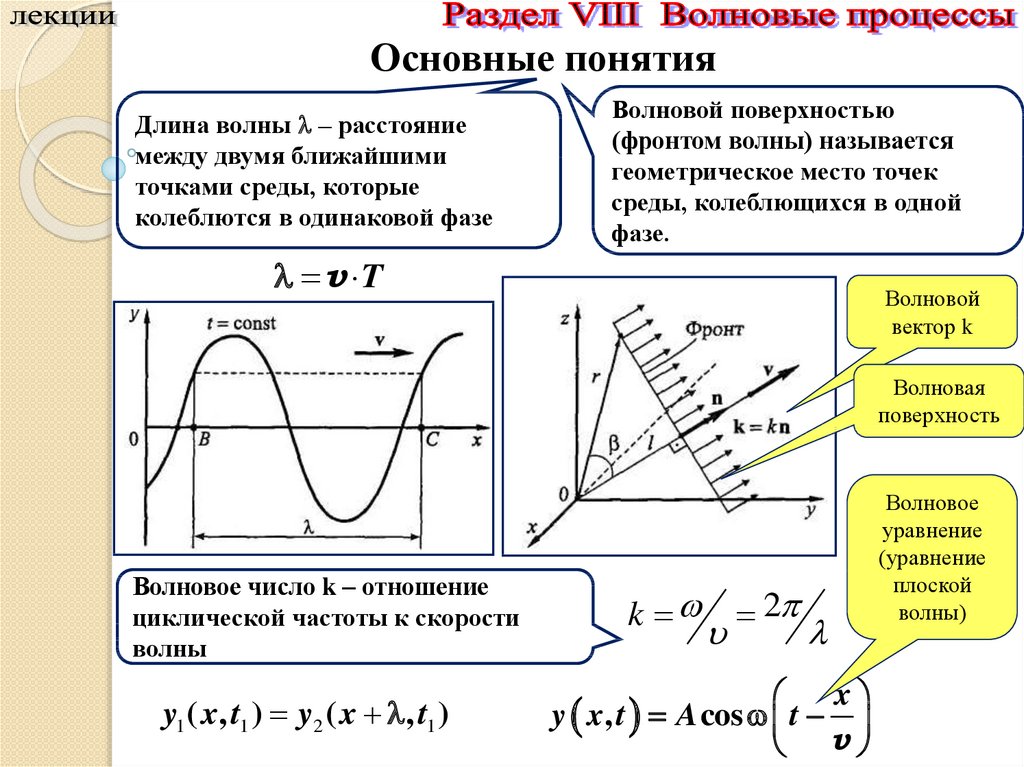
Основные понятияДлина волны – расстояние
между двумя ближайшими
точками среды, которые
колеблются в одинаковой фазе
Волновой поверхностью
(фронтом волны) называется
геометрическое место точек
среды, колеблющихся в одной
фазе.
v T
Волновой
вектор k
Волновая
поверхность
Волновое число k – отношение
циклической частоты к скорости
волны
y1 ( x, t1 ) y2 ( x , t1 )
k 2
x
y x , t A cos t
v
Волновое
уравнение
(уравнение
плоской
волны)
4.
Основные понятияx
a cos t a cos t
u
( x, t )
x
2
a cos t
2
dt
u
2
( x, t )
a
x
2 cos t
2
dx
u
u
2
2
x
t 0
u
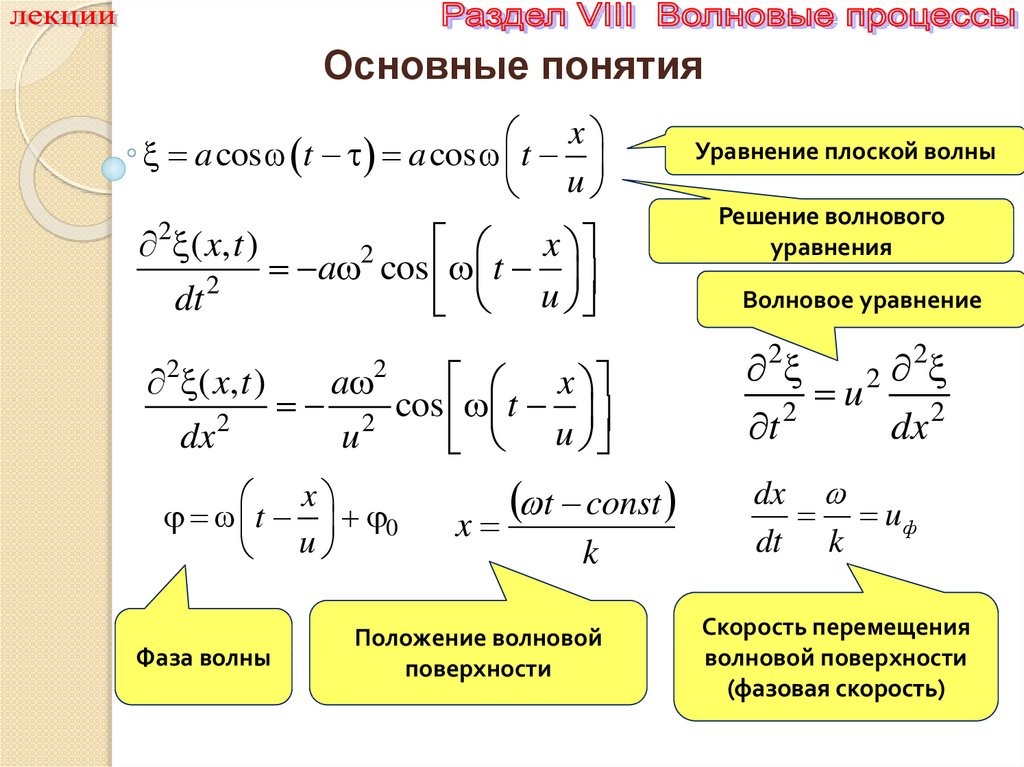
Фаза волны
t const
x
k
Положение волновой
поверхности
Уравнение плоской волны
Решение волнового
уравнения
Волновое уравнение
2
2
2
u
2
t
dx 2
dx
uф
dt k
Скорость перемещения
волновой поверхности
(фазовая скорость)
5.
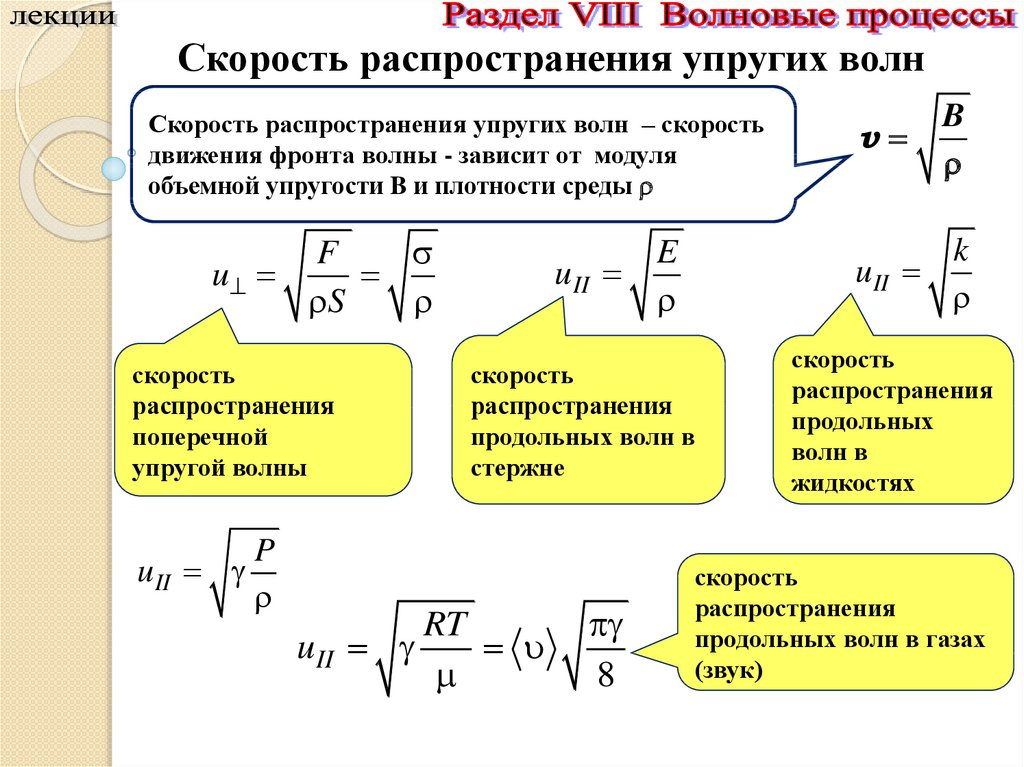
Скорость распространения упругих волнСкорость распространения упругих волн – скорость
движения фронта волны - зависит от модуля
объемной упругости B и плотности среды
F
u
S
скорость
распространения
поперечной
упругой волны
P
u II
u II
k
u II
E
скорость
распространения
продольных волн в
стержне
RT
uII
8
v
B
скорость
распространения
продольных
волн в
жидкостях
скорость
распространения
продольных волн в газах
(звук)
6.
Упругие волныПринцип суперпозиции
1 a cos 1t k1 x 0
упругих волн: если две
волны являются
решением волнового
уравнения, то решением
является и их линейная
комбинация
Дисперсия волн зависимость скорости
распространения волн в
среде от длины волны.
u f f
2 a cos 2t k2 x 0
1 2
1
k1
2
k2
u
7.
Групповая скорость1 a cos 1t k1x
an cos nt k n x n
2 a cos 2t k2 x
n 1
a cos 1t k1 x a cos 2t k 2 x 2 1 1
k 2 k1
2 1
2a cos
t
2
2
A( x ,t ) cos t kx
Модулирующая
волна биений
2
Tм
k 2 k1
2 1
x cos
t
2
2
2
м
k
A( x,t ) 2a cos t kx
x
Несущая волна
2
4
Tн
2 1
2
4
н
k
k 2 k1
8.
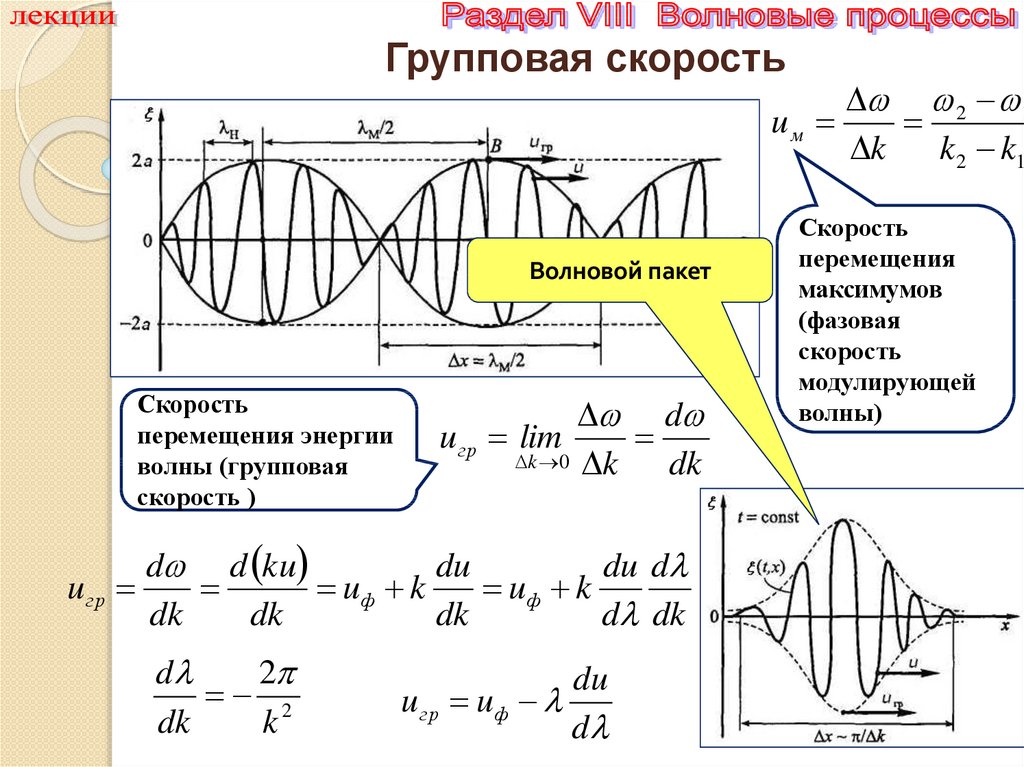
Групповая скорость2 1
uм
k
k 2 k1
Волновой пакет
Скорость
перемещения энергии
волны (групповая
скорость )
d
u гр lim
k 0 k
dk
d d ku
du
du d
u гр
uф k
uф k
dk
dk
dk
d dk
d
2
2
dk
k
u гр uф
du
d
Скорость
перемещения
максимумов
(фазовая
скорость
модулирующей
волны)
9.
Энергия упругой волныЭнергия волны в упругой среде состоит из
кинетической энергии частиц вещества,
совершающих небольшие колебания, и из
потенциальной энергии упругой
деформации среды.
x
a cos t
u
x
u
a sin t
t
u
1
1
x
2
2 2
2
Ек mu S x a sin t
2
2
u
Ек 1 2 2 2 x
к
a sin t
S x 2
u
Плотность кинетической энергии в точке x в момент времени t
10.
Энергия упругой волны1
1
2
En k ( ) S xE
2
2
x
2
x
a cos t
u
t1x x t1x
x
x
x
a sin t
x
x u
u
t1x x t1x
2
1
x
2
En S xE a sin t
2
u
u
Плотность
потенциальной
энергии в точке x в
момент времени t
En 1 2 2 2 x
n
E 2 a sin t
S x 2 u
u
11.
Энергия упругой волныЕк 1 2 2 2 x
к
a sin t
S x 2
u
En 1 2 2 2 x
n
E 2 a sin t
S x 2 u
u
x
n k a sin t
u
2 2
2
Плотность энергии в точке x в
момент времени t
1 2 2
a
2
Средняя плотность энергии
12.
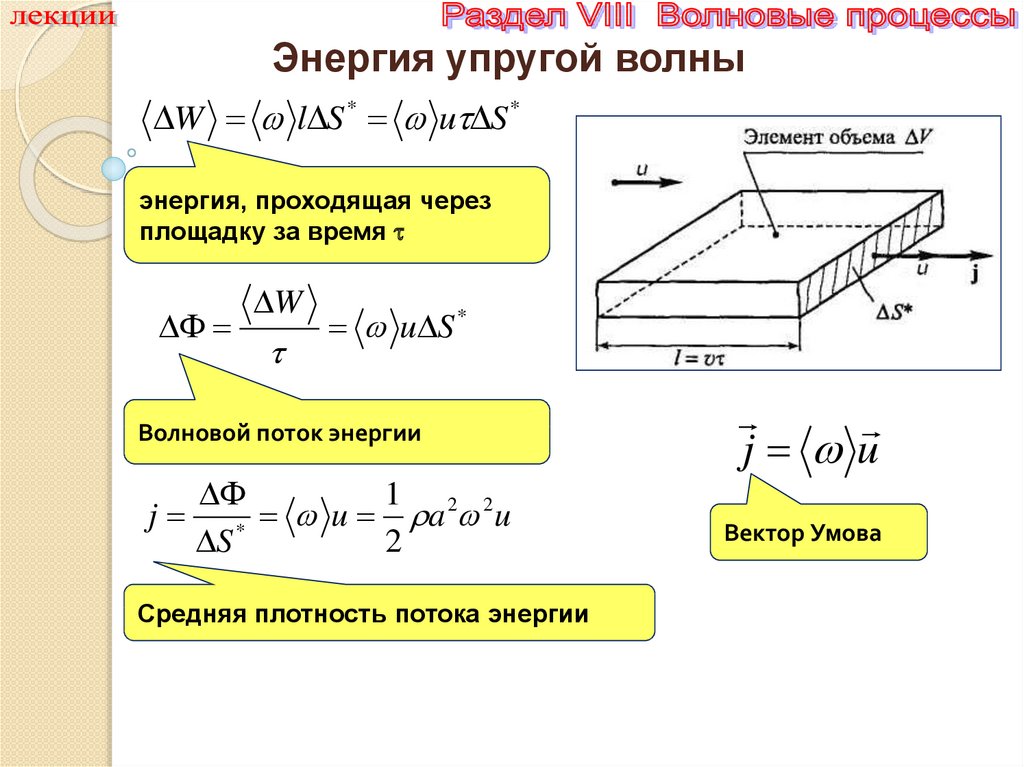
Энергия упругой волныW l S* u S*
энергия, проходящая через
площадку за время
W
u S *
Волновой поток энергии
1 2 2
j * u a u
S
2
Средняя плотность потока энергии
j u
Вектор Умова
13.
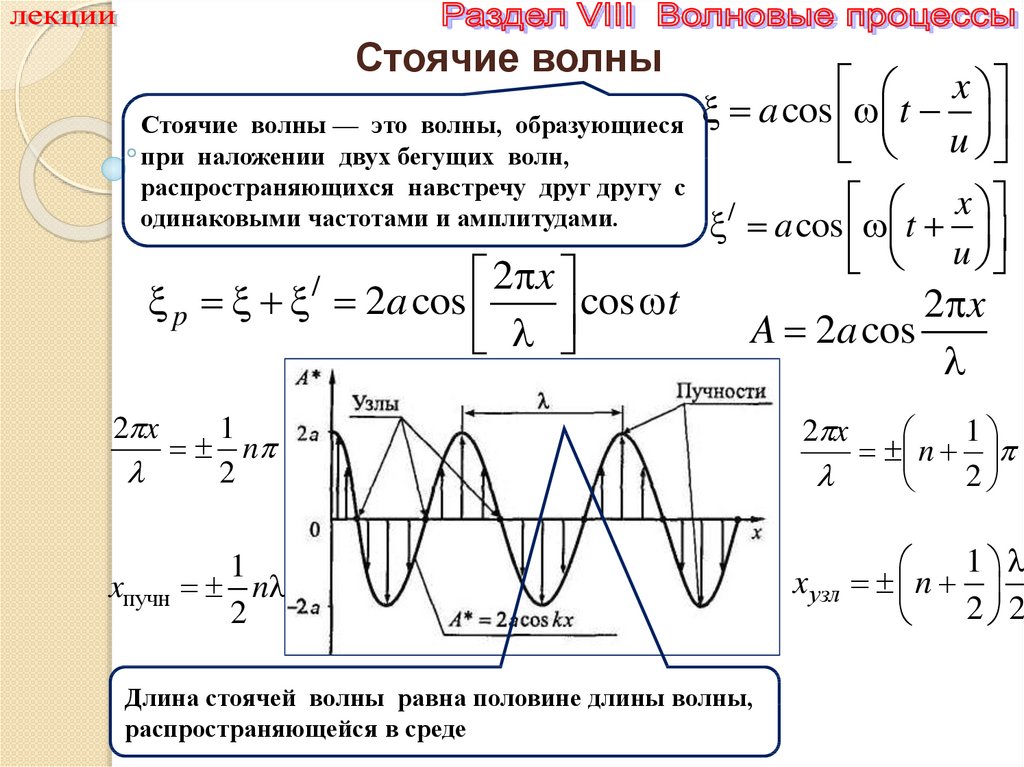
Стоячие волныСтоячие волны — это волны, образующиеся
при наложении двух бегущих волн,
распространяющихся навстречу друг другу с
одинаковыми частотами и амплитудами.
2 x
p 2a cos
cos t
/
x
a cos t
u
x
a cos t
u
/
2 x
A 2a cos
2 x
1
n
2
1
xпучн n
2
Длина стоячей волны равна половине длины волны,
распространяющейся в среде
2 x
1
n
2
x узл
1
n
2 2
14.
Стоячие волны15.
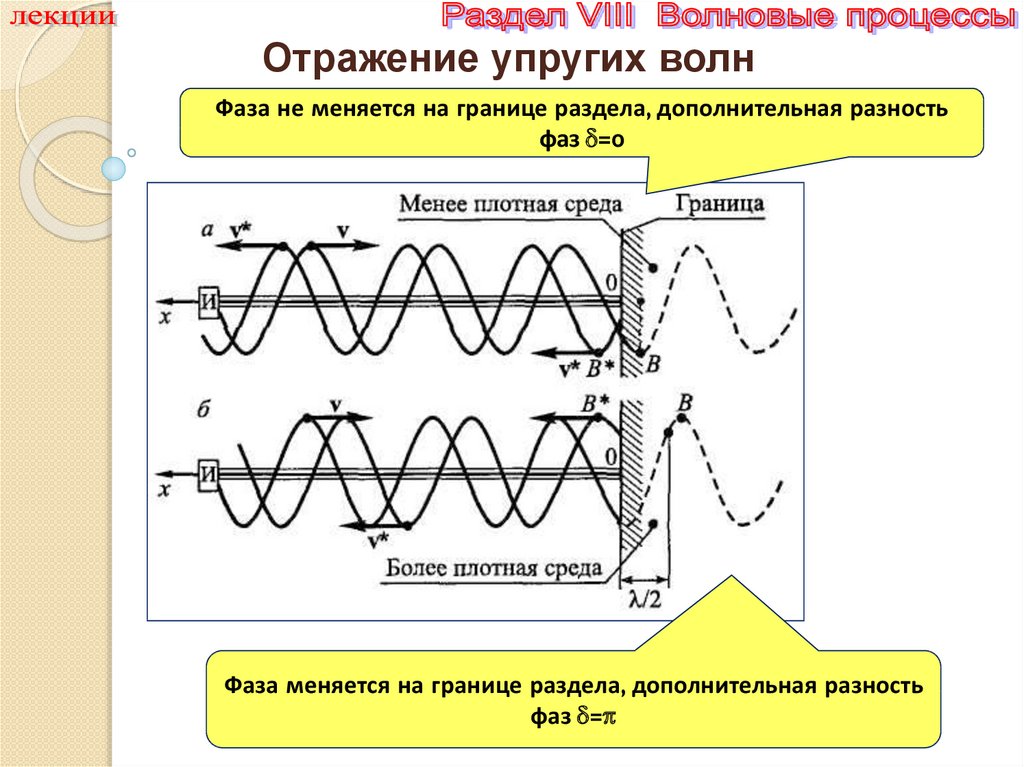
Отражение упругих волнФаза не меняется на границе раздела, дополнительная разность
фаз =0
Фаза меняется на границе раздела, дополнительная разность
фаз =
16.
Интерференция волнИнтерференцией волн называется явление наложения когерентных
волн, при котором происходит устойчивое во времени их взаимное
усиление в одних точках пространства и ослабление в других в
зависимости от соотношения между фазами этих волн.
Когерентностью
называется согласованное
протекание во времени и
пространстве нескольких
колебательных или
волновых процессов.
s1 a1 cos t 1
s2 a2 cos t 2
1 k1 x1
s a cos t
2 k2 x2
17.
Интерференция волнs a cos t
a a12 a22 2a1a2 cos 2 1
1 2 k x2 x1
1 2 2 n
2 x2 x1
2 n
x2 x1 n
a a1 a2
Условие
интерференционного
максимума
2 x2 x1
1 2 2n 1
2 x2 x1
2 n
x2 x1 2n 1
2
a a1 a2
Условие
интерференционного
минимума
18.
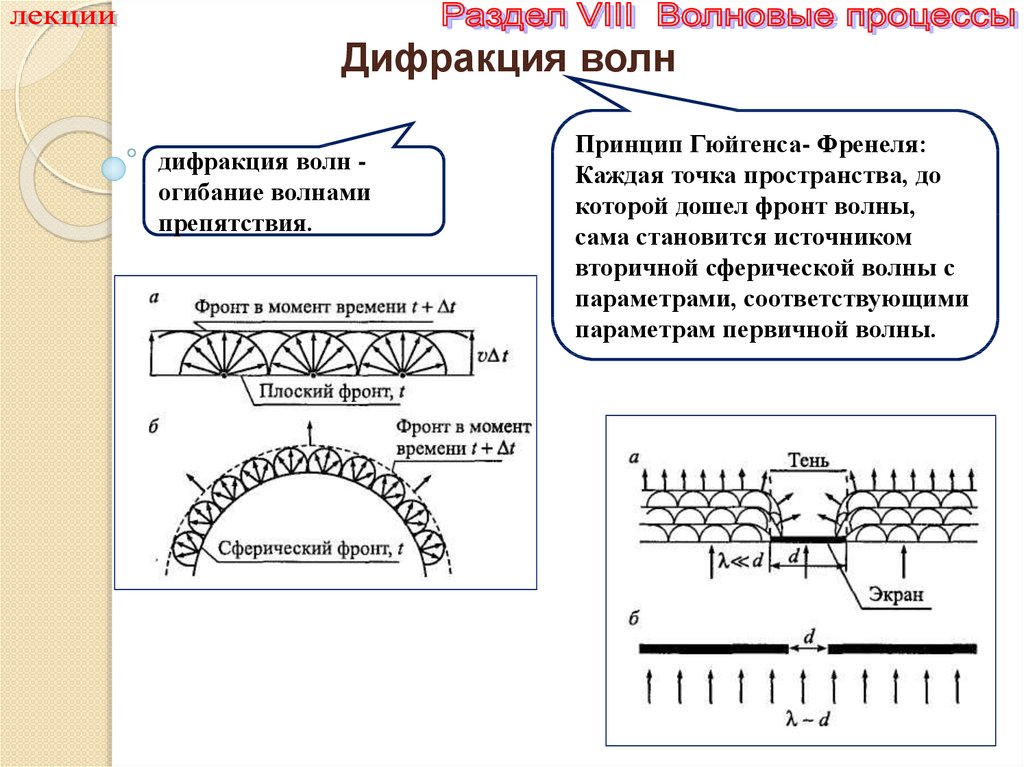
Дифракция волндифракция волн огибание волнами
препятствия.
Принцип Гюйгенса- Френеля:
Каждая точка пространства, до
которой дошел фронт волны,
сама становится источником
вторичной сферической волны с
параметрами, соответствующими
параметрам первичной волны.
19.
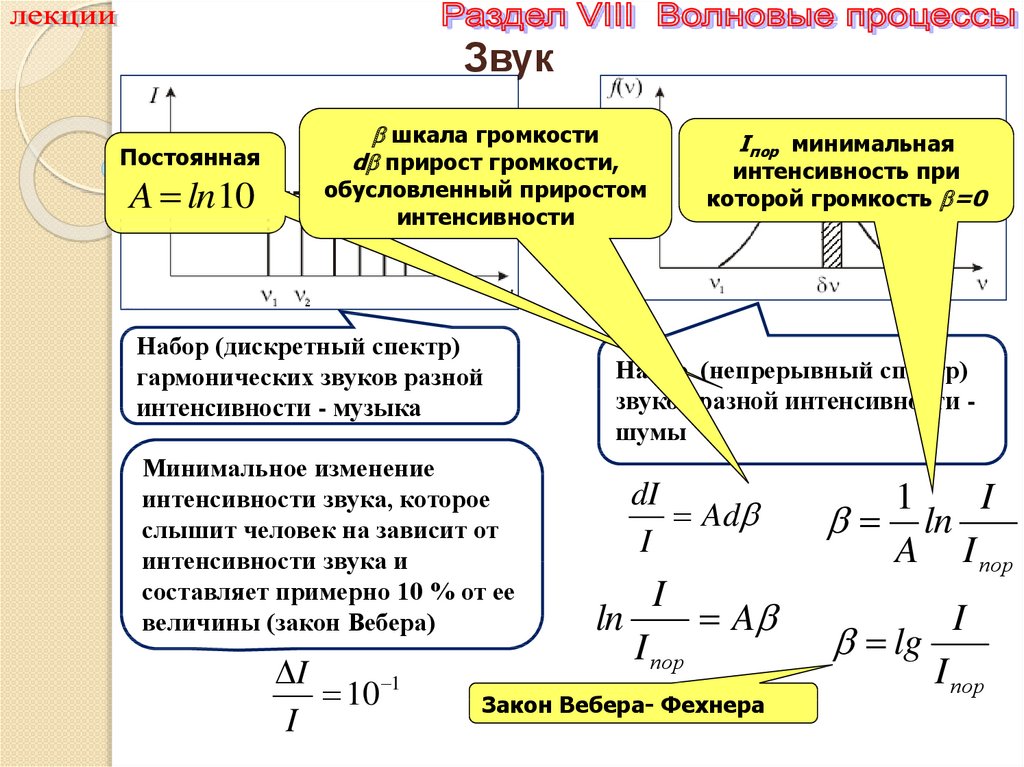
ЗвукПостоянная
A ln10
шкала громкости
d прирост громкости,
обусловленный приростом
Iпор минимальная
интенсивность при
которой громкость =0
интенсивности
Набор (дискретный спектр)
гармонических звуков разной
интенсивности - музыка
Минимальное изменение
интенсивности звука, которое
слышит человек на зависит от
интенсивности звука и
составляет примерно 10 % от ее
величины (закон Вебера)
I
10 1
I
Набор (непрерывный спектр)
звуков разной интенсивности шумы
dI
Ad
I
ln
I
I пор
A
Закон Вебера- Фехнера
1
I
ln
A I пор
lg
I
I пор
20.
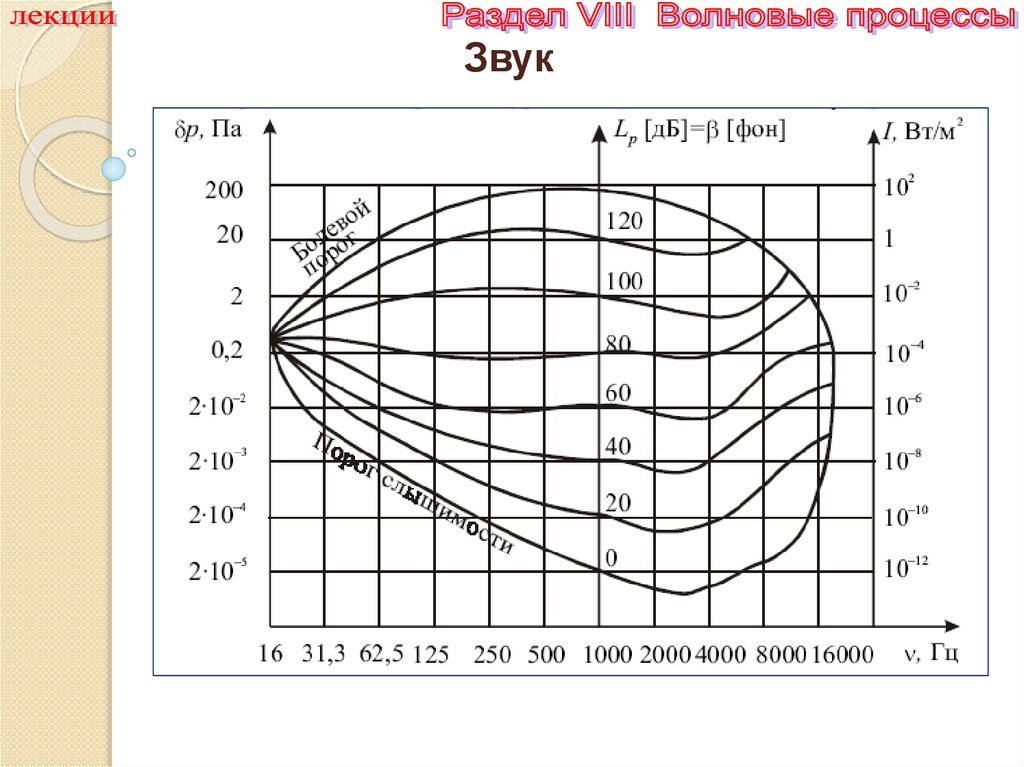
Звук21.
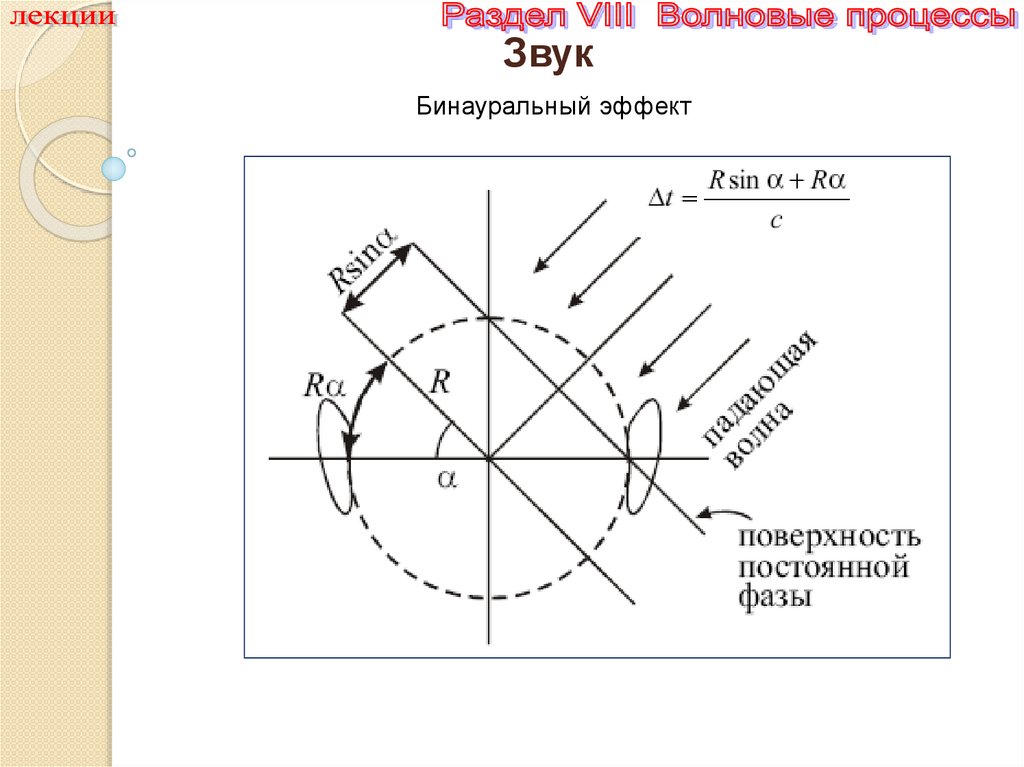
ЗвукБинауральный эффект
22.
ЭФФЕКТ ДОПЛЕРАЭффектом Доплера называется изменение частоты колебаний,
воспринимаемой приемником, при движении источника этих
колебаний и приемника друг относительно друга.
0 d ист T0
1
0
1 ист
0 d ист T0
пр
пр
0 1
0
0
1
пр
1 ист
23.
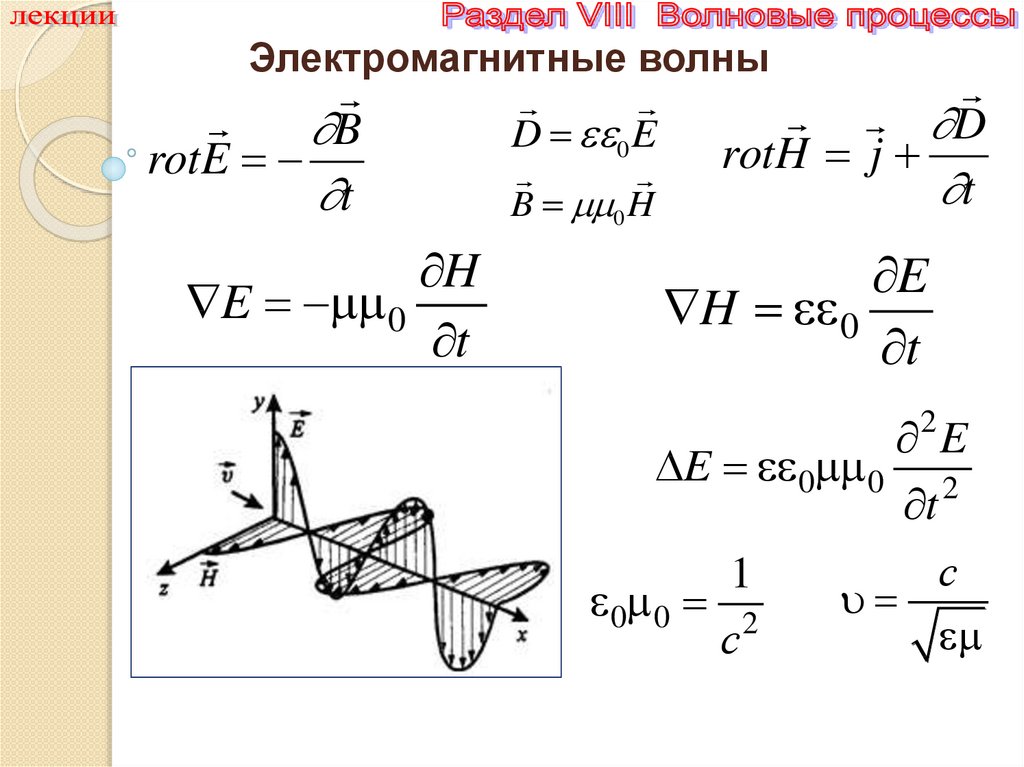
Электромагнитные волныB
D 0 E
rotE
t
H
E 0
t
B 0 H
D
rotH j
t
E
H 0
t
E
E 0 0 2
t
2
1
0 0 2
с
с
24.
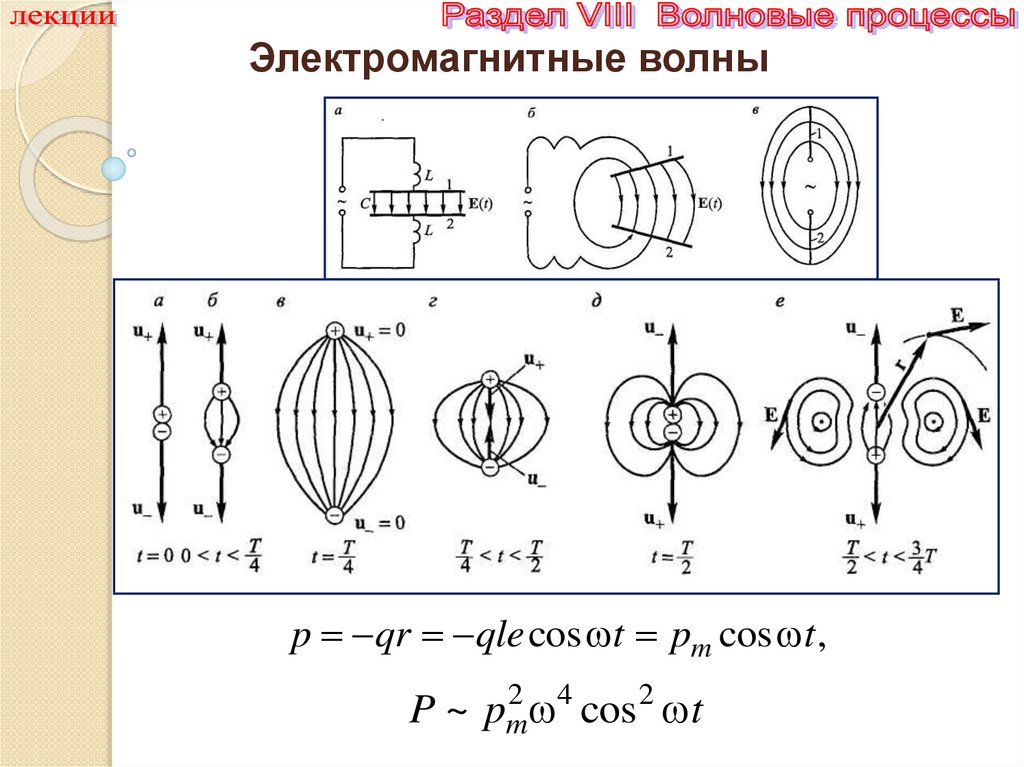
Электромагнитные волныp qr qle cos t pm cos t ,
P ~ pm2 4 cos 2 t
25.
Электромагнитные волныВектор
2 Пойнтинга
2
(Умова – Пойнтинга)
E E E 2 E
2 2 2 2
2
x
y
z
c t
2
2 H 2 H 2 H 2 H
2 2 2 2
2
x
y
z
c t
0 E 2 0 H 2
w wE wH
.
2
2
D 0 E
B 0 H
1
w 0 0 EH EH ,
S w EH .
S EH
S
4 sin 2
r2











 Физика
Физика








