Математическая модель задачи

1. Математика, правильно понятая, обладает не только истинной, но и величайшей красотой.

Бертран Рассел

2. Разминка. Тест

Вариант 1
Вариант 2
1. Cos ( 90⁰ - α) =
1. Sin ( 90⁰ - α)
2. Sin ( 180⁰- α) =
2. Cos (180⁰ - α)
3. Sin 60⁰ =
3. Cos 60⁰ =
4. Cos 45⁰ =
4. Sin 45⁰ =
5. Sin 30⁰ =
5. Cos 30⁰ =

3. Проверка

Вариант 1
Вариант 2
1. sin α
1. cos α
2. sin α
2. -cos α
3.
3.
4.
4.
5.
5.

4. Задача. Используя данные, указанные на рисунке, найдите расстояние между недоступными пунктами А и В, расположенными на разных

берегах озера.

5. Математическая модель задачи

Используя данные, указанные на рисунке,
найдите расстояние между недоступными
пунктами А и В, расположенными на
разных берегах озера.

6.

Записать
формулу нахождения
расстояния между точками по их
координатам.
Работа в группе (решение задачи)

7.

C
С b cos A; b sin A
у
b
А
a
с
AB=с
BC=a
CA=b
B(c;0)
х
B
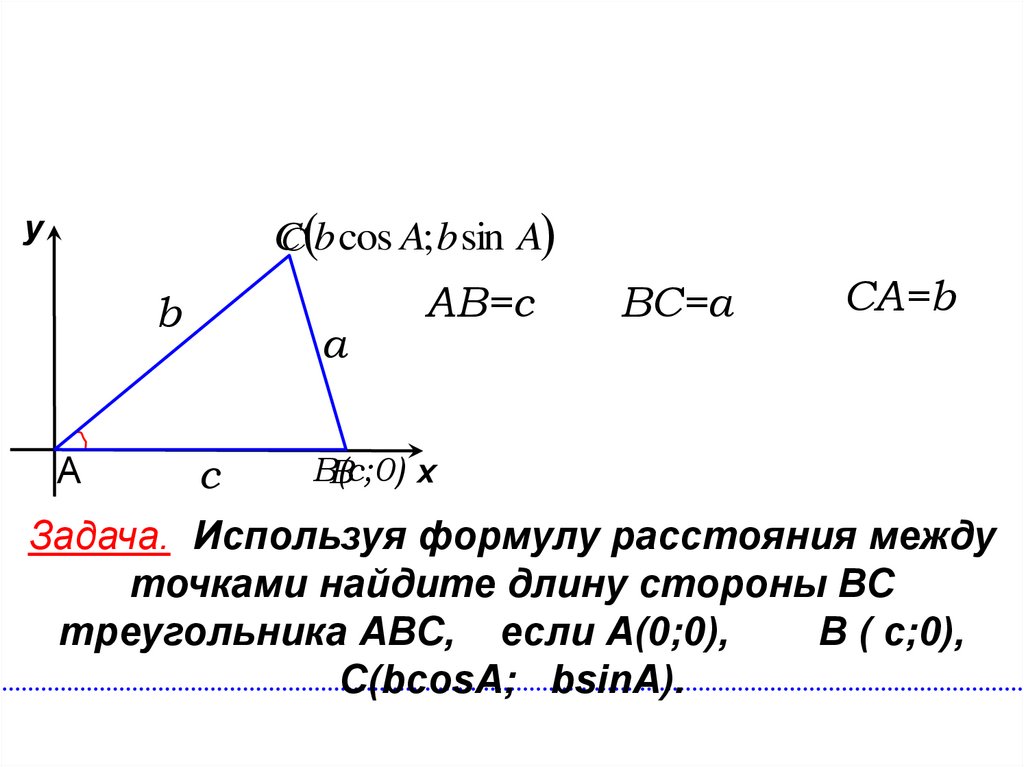
Задача. Используя формулу расстояния между
точками найдите длину стороны ВС
треугольника АВС, если А(0;0),
В ( с;0),
С(bcosA; bsinA).

8. Проверим:

BC a b cos A c b sin A
2
2
2
2
2
b cos A b sin A 2bc cos A c
2
2
b c 2bc cos A
2
2
2
2
2
a b c 2bc cos A
2
2
2

9.

ТЕОРЕМА
КОСИНУСОВ

10. Работа с учебником

Стр.257,
п.98,
рис.293
Составить
план доказательства теоремы
косинусов

11.

ОБОБЩЕННАЯ ТЕОРЕМА ПИФАГОРА
КВАДРАТ СТОРОНЫ ТРЕУГОЛЬНИКА РАВЕН СУММЕ
КВАДРАТОВ ДВУХ ДРУГИХ СТОРОН МИНУС
УДВОЕННОЕ ПРОИЗВЕДЕНИЕ ЭТИХ СТОРОН НА
КОСИНУС УГЛА МЕЖДУ НИМИ
у
C
С b cos A; b sin A
b
А
a
с
AB=с
CA=b
BC=a
a b c 2bc cos A
2
2
2
B(c;0)
х
B
BC a b cos A c b sin A
b 2 cos 2 A b 2 sin 2 A 2bc cos A c 2
b 2 c 2 2bc cos A
2
2
2
a b c
A 90
2
2
2
2
2

12. Сферическая тригонометрия

рассматривает треугольники на сфере и
позволяет находить одни элементы этих
треугольников по другим их элементам.

13. Замечательная сферическая теорема косинусов cos a = cos b cos c + sin b sin c cos A.

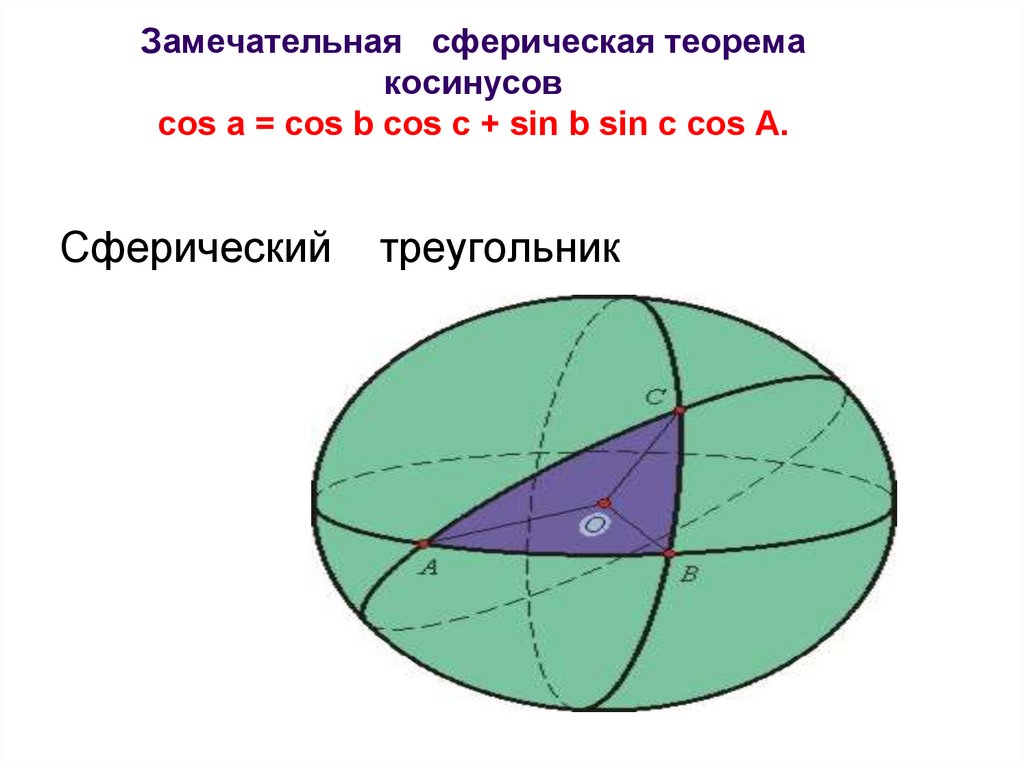
Замечательная сферическая теорема
косинусов
cos a = cos b cos c + sin b sin c cos A.
Сферический
треугольник

14.

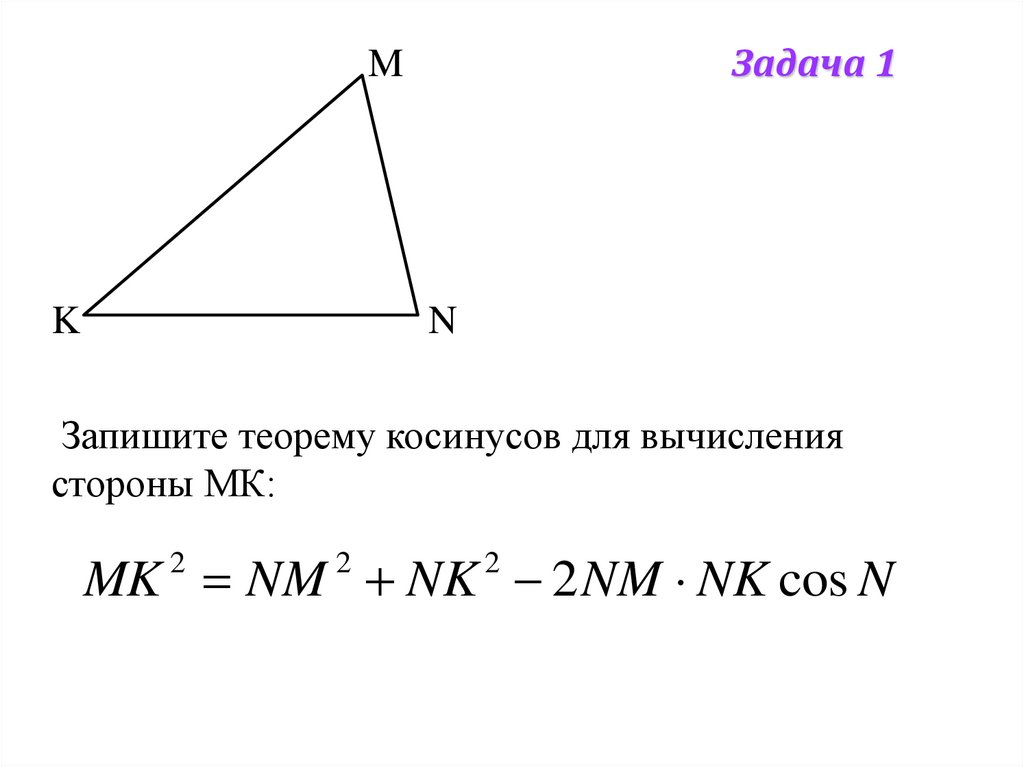
Задача 1
M
K
N
Запишите теорему косинусов для вычисления
стороны МК:
MK NM NK 2 NM NK cos N
2
2
2

15.

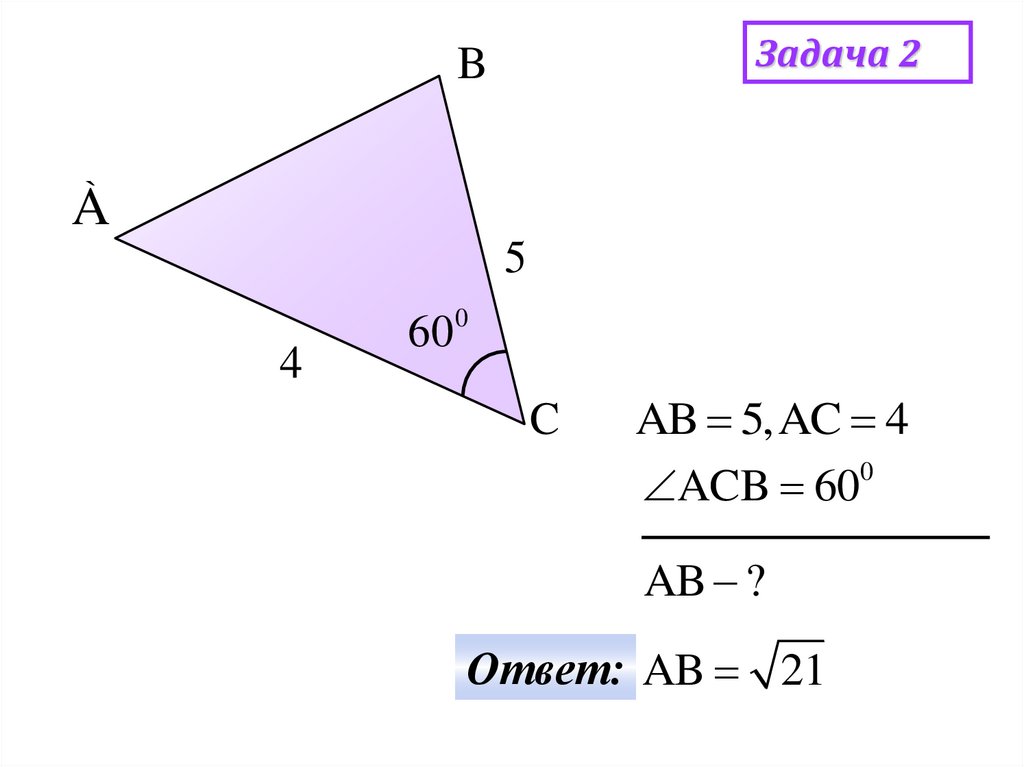
Задача 2
B
À
5
4
600
C
AB 5,AC 4
ACB 600
AB ?
Ответ: AB 21

16.

какое количество
элементов должно
быть известно, чтобы
задача была решена?
B
À
5
4
600
C
Какую задачу можно решать, используя теорему
косинусов?

17. Какую задачу можно решать, используя теорему косинусов?

Задача 1.
нахождение длины третьей стороны по
известным двум другим и углу между
ними

18. Выразим косинус угла из теоремы косинусов

АВ AC BC 2 AC BC cos C
2
2
2
2 АС ВС cos C AC BC AB
2
2
AC BC AC
cos C
2 AC BC
2
2
2
2

19. Что можно находить по этой формуле?

AC BC AC
cos C
2 AC BC
2
2
2

20. Что можно находить по этой формуле?

Задача 2.
угол (или косинус угла)
треугольника по трем
известным сторонам

21.

ГИА
Открытый банк заданий
по математике.

22.

Задание
(№ 169935)
Какие из следующих утверждений верны?
1
Квадрат любой стороны тр-ка равен сумме
квадратов двух других сторон без удвоенного
произвед-ия этих сторон на sin угла между ними.
2
Если катеты прямоугольного треугольника
равны 5 и 12, то его гипотенуза равна 13.
3
Треугольник ABC, у которого АВ=5, ВС=6, АС=7,
является остроугольным.
4
В прямоугольном треугольнике
квадрат катета равен разности квадратов
гипотенузы и другого катета.

23.

Задача о футболисте.
Футбольный мяч находится в
точке А футбольного поля на
расстояниях 23 м и 24 м от
оснований В и С стоек ворот.
С
В
7м
Футболист направляет мяч в
ворота. Найдите угол α
попадания мяча в ворота,
если ширина ворот равна 7 м.
α
А

24.

Математическая модель задачи
С
В
7м
найдем угол А, равный α.
По теореме косинусов
определим cos A
AB 2 AC 2 BC 2
cos A
2 AB AC
α
А
Угол α находим по таблице:
α ≈ 16 57

25. Вычислить косинус большего угла в треугольнике с известными длинами трех сторон и определить вид этого треугольника.

Вариант №1
Вариант №2
c = 6, b = 8, c = 6, b = 8,
a=9
a = 10
Вариант №3
c = 6, b = 8,
a = 11

26. Проверка

Вариант №1
Вариант №2
Вариант №3
c = 6, b = 8, a = 9 c = 6, b = 8, a = 10 c = 6, b = 8, a = 11
cosa =19/96
cosa = 0
cosa = 0
cosa > 0
cosa = 0
cosa < 0
треугольник
треугольник
остроугольный прямоугольный
треугольник
тупоугольный

27. Сравнить квадрат наибольшей стороны с суммой квадратов двух других сторон и записать сравнение в виде равенства или

неравенства.
Вариант №1
Вариант №2
Вариант №3
c = 6, b = 8, a = 9 c = 6, b = 8, a = 10 c = 6, b = 8, a = 11
треугольник
треугольник
остроугольный прямоугольный
треугольник
тупоугольный

28. Проверка

Вариант №1
Вариант №2
Вариант №3
c = 6, b = 8, a = 9 c = 6, b = 8, a = 10 c = 6, b = 8, a = 11
81<100
a2< с2 + b2
100 = 100
a2 = с2 + b2
треугольник
треугольник
остроугольный прямоугольный
121 > 100
a2 > с2 + b2
треугольник
тупоугольный

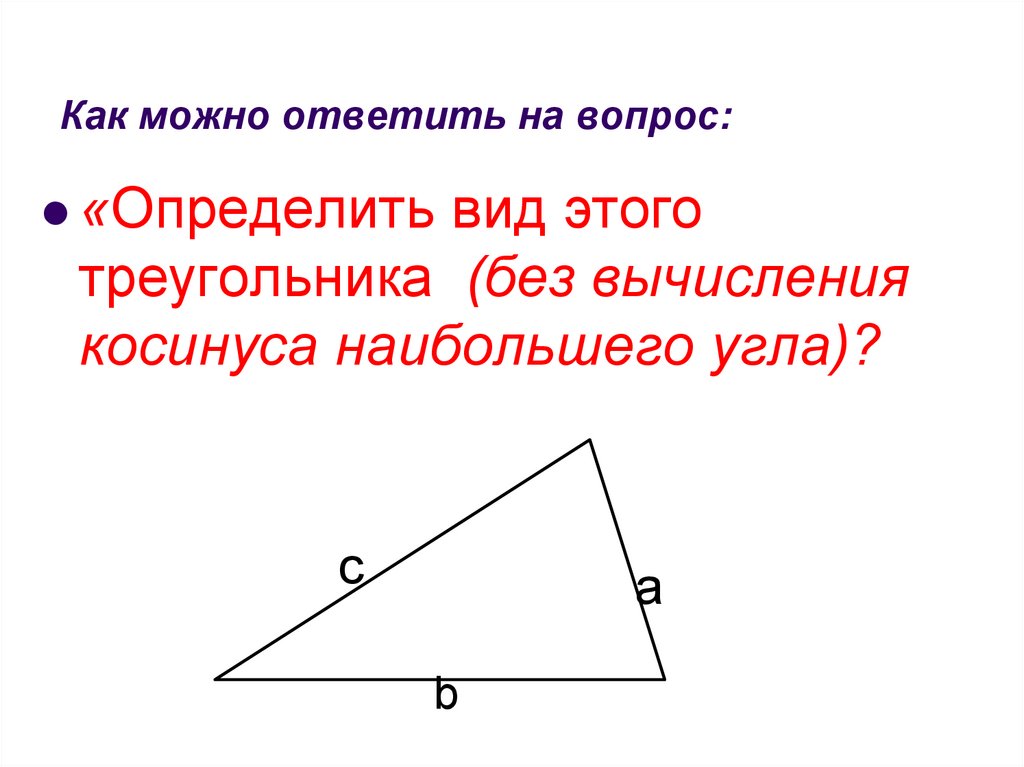
29. Как можно ответить на вопрос:

«Определить вид этого
треугольника (без вычисления
косинуса наибольшего угла)?
с
а
b

30. Как можно ответить на вопрос: «Определить вид этого треугольника» без вычисления косинуса наибольшего угла?

Пусть с – наибольшая сторона
– если с2 < a2 + b2, то треугольник
остроугольный;
– если с2 = a2 + b2, то треугольник
прямоугольный;
– если с2 > a2 + b2, то треугольник
тупоугольный.

31. Какие задачи можно решить с помощью теоремы косинусов?

находить длину третьей стороны по
известным двум другим и углу между
ними;
определять угол (косинус угла)
треугольника по трем известным
сторонам
определять вид треугольника по трем
известным сторонам

32.

Мини-тест

33.

№
1
2
3
4
Варианты ответа
В) p2 = m2 + n2 - 2mn cosα
В) тупоугольный.
В) √5
В) тупоугольный

34. Домашнее задание

П.98 прочитать
Подготовить
доказательство
(презентацию доказательства)
теоремы косинусов
№ 1025 (ж)
№1031