Похожие презентации:
Взаимное пересечение поверхностей
1. Взаимное пересечение поверхностей Вид линии пересечения зависит от сочетаний пересекающихся поверхностей ● ДВЕ ПОВЕРХНОСТИ ВРАЩЕНИЯ (ОБ
Взаимное пересечениеповерхностей
Вид линии пересечения зависит от
сочетаний пересекающихся поверхностей
● ДВЕ ПОВЕРХНОСТИ ВРАЩЕНИЯ (ОБЩИЙ СЛУЧАЙ)
ЛИНИЯ ПЕРЕСЕЧЕНИЯ - ПРОСТРАНСТВЕННАЯ КРИВАЯ
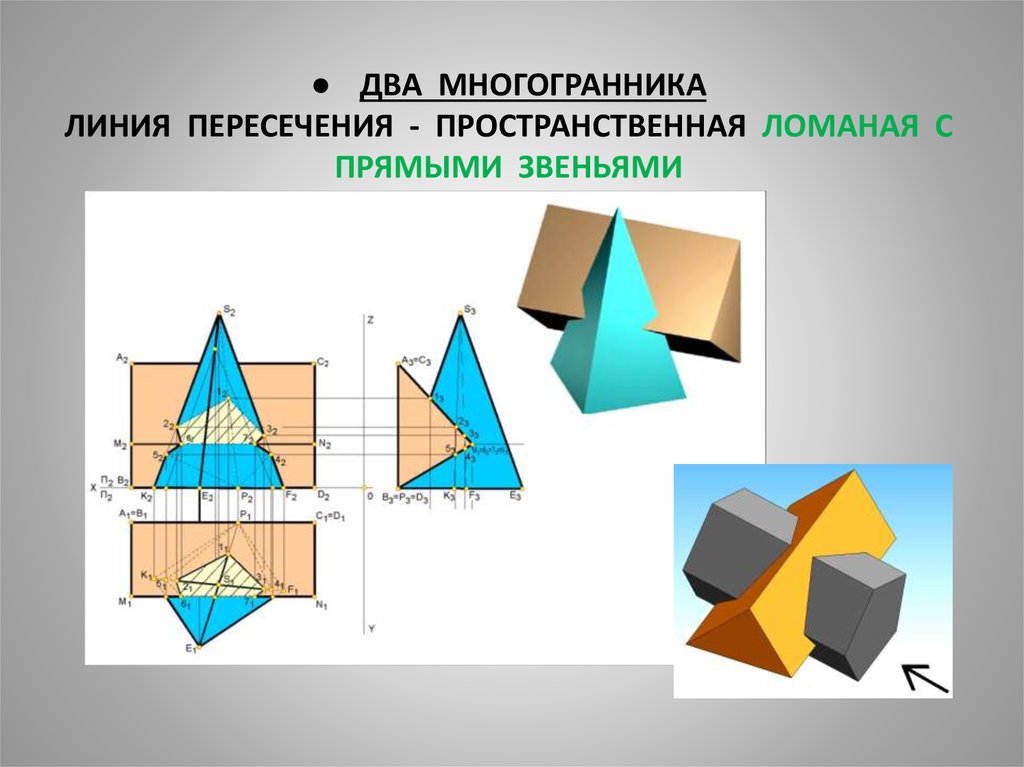
2. ● ДВА МНОГОГРАННИКА ЛИНИЯ ПЕРЕСЕЧЕНИЯ - ПРОСТРАНСТВЕННАЯ ЛОМАНАЯ С ПРЯМЫМИ ЗВЕНЬЯМИ
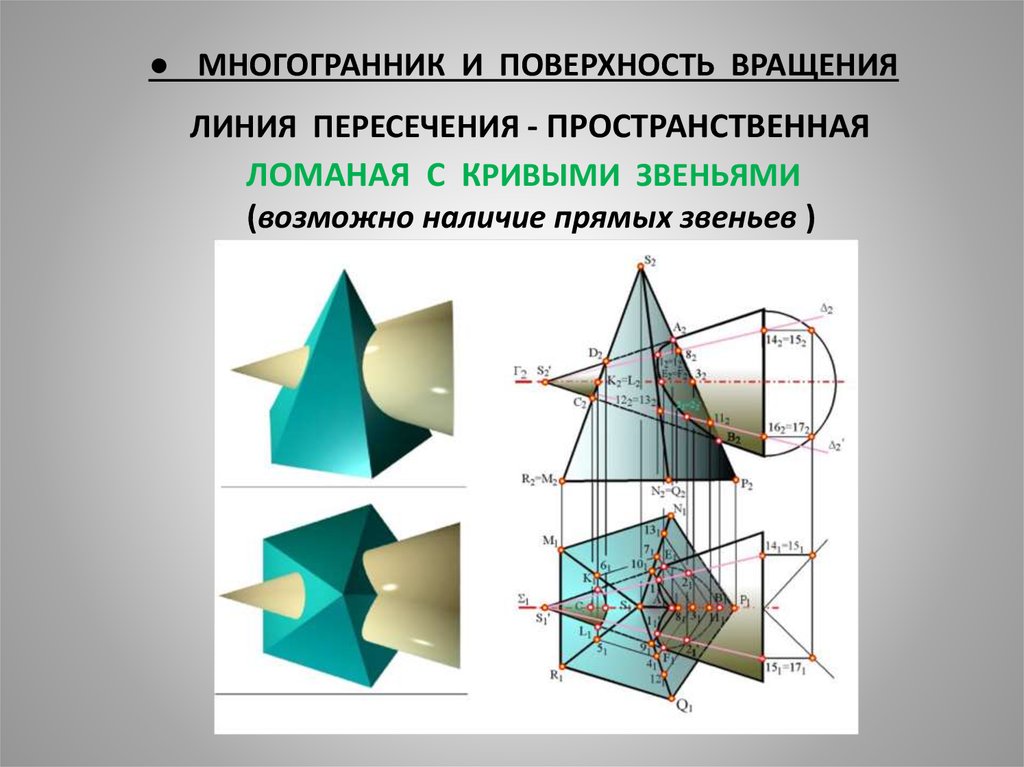
3. ● МНОГОГРАННИК И ПОВЕРХНОСТЬ ВРАЩЕНИЯ ЛИНИЯ ПЕРЕСЕЧЕНИЯ - ПРОСТРАНСТВЕННАЯ ЛОМАНАЯ С КРИВЫМИ ЗВЕНЬЯМИ (возможно наличие прямых звеньев )
4. ПЕРЕСЕЧЕНИЕ МОЖЕТ БЫТЬ ПОЛНЫМ и НЕПОЛНЫМ (ВРЕЗАНИЕ) В ПЕРВОМ СЛУЧАЕ - ДВА ЗАМКНУТЫХ КОНТУРА ЛИНИИ ПЕРЕСЕЧЕНИЯ ПРИ ВРЕЗАНИИ - ОДИН ЗАМКНУТЫЙ
ПЕРЕСЕЧЕНИЕ МОЖЕТ БЫТЬПОЛНЫМ и НЕПОЛНЫМ (ВРЕЗАНИЕ)
В ПЕРВОМ СЛУЧАЕ - ДВА ЗАМКНУТЫХ КОНТУРА ЛИНИИ
ПЕРЕСЕЧЕНИЯ
ПРИ ВРЕЗАНИИ - ОДИН ЗАМКНУТЫЙ КОНТУР
5. СПОСОБЫ ПОСТРОЕНИЯ ТОЧЕК, ПРИНАДЛЕЖАЩИХ ЛИНИИ ПЕРЕСЕЧЕНИЯ: 1. Способ секущих плоскостей 2. Способ сфер Концентрических Эксцентрических
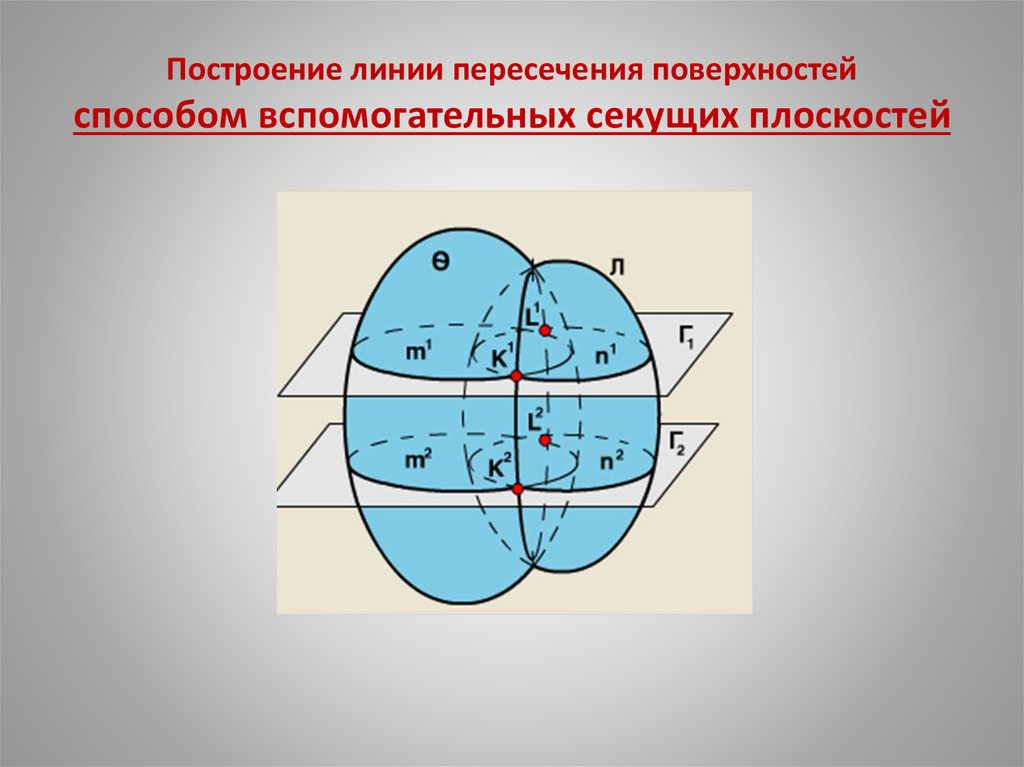
6. Построение линии пересечения поверхностей способом вспомогательных секущих плоскостей
7.
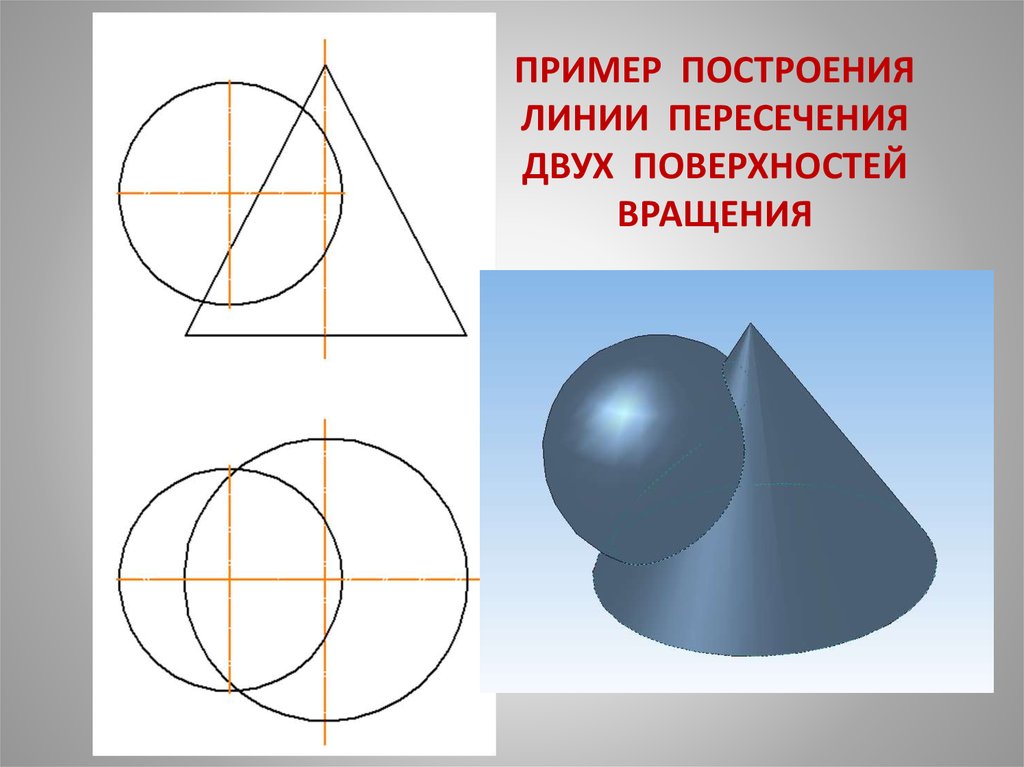
8. ПРИМЕР ПОСТРОЕНИЯ ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ
9. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ 1 АНАЛИЗ УСЛОВИЯ (Какая линия? Сколько? Способ построения точек?) 2 ХАРАКТЕРНЫЕ ТОЧКИ (обозначить) 3 ДОПОЛНИТЕЛЬНЫЕ
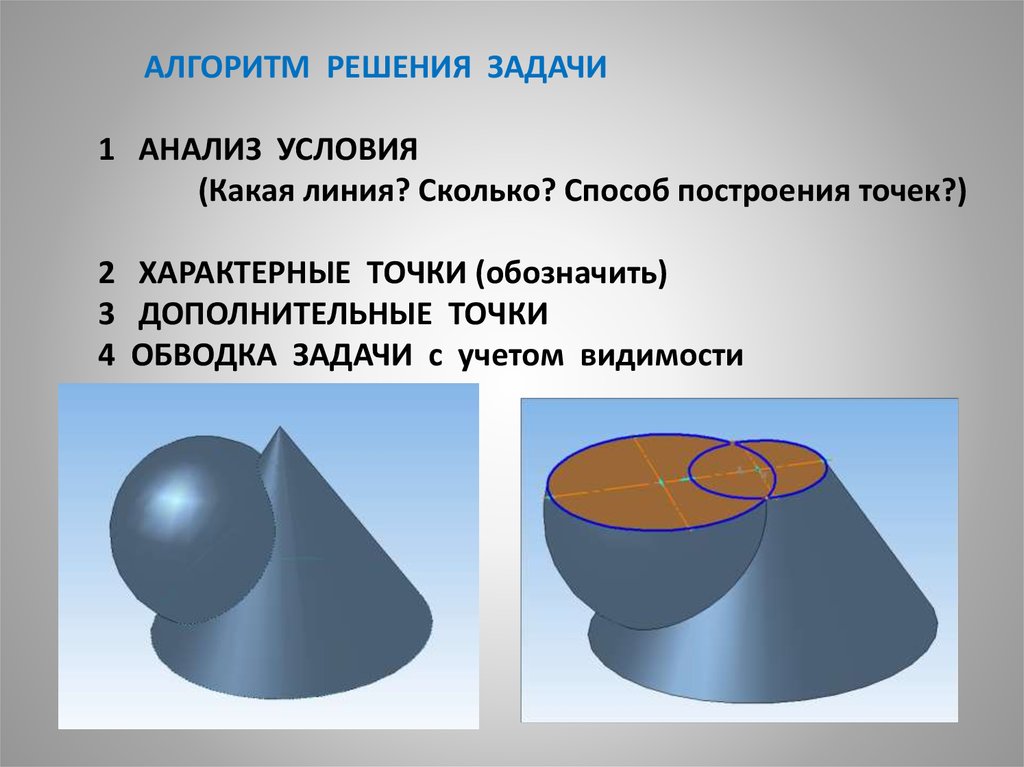
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ1 АНАЛИЗ УСЛОВИЯ
(Какая линия? Сколько? Способ построения точек?)
2 ХАРАКТЕРНЫЕ ТОЧКИ (обозначить)
3 ДОПОЛНИТЕЛЬНЫЕ ТОЧКИ
4 ОБВОДКА ЗАДАЧИ с учетом видимости
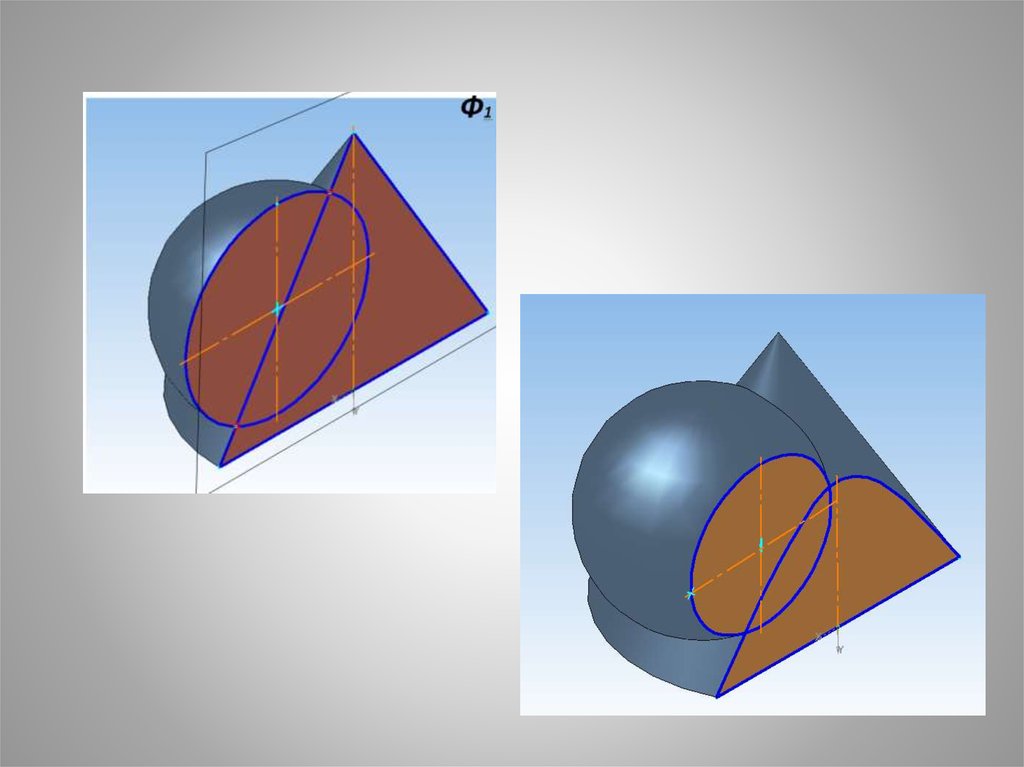
10.
11.
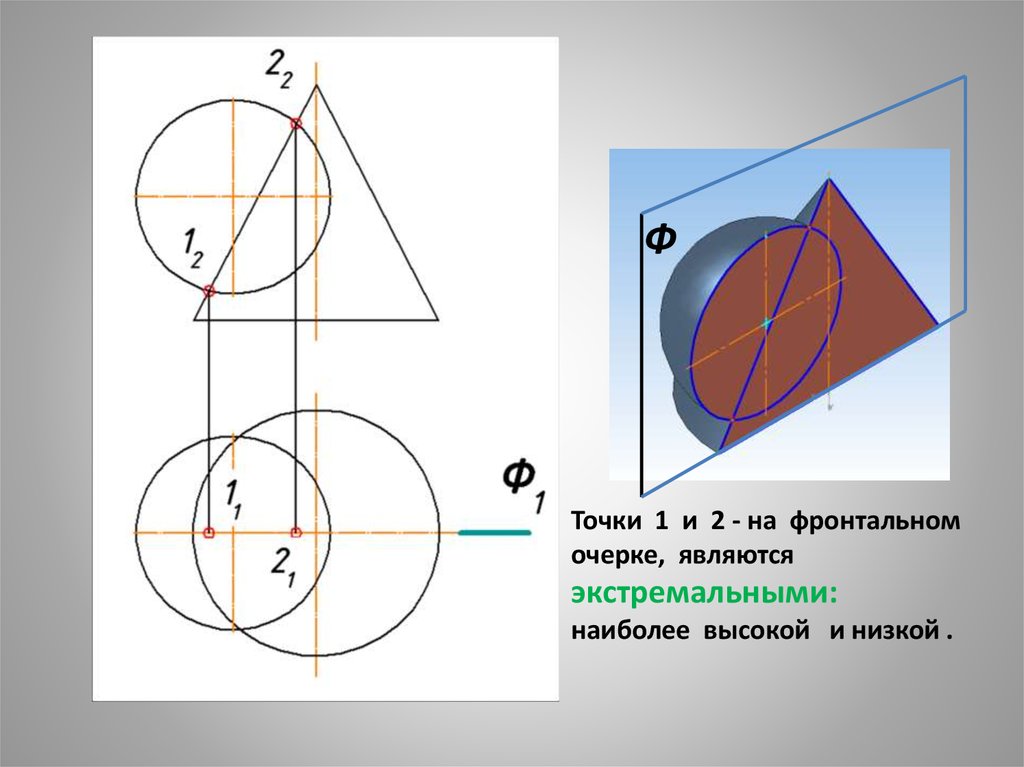
ФТочки 1 и 2 - на фронтальном
очерке, являются
экстремальными:
наиболее высокой и низкой .
12.
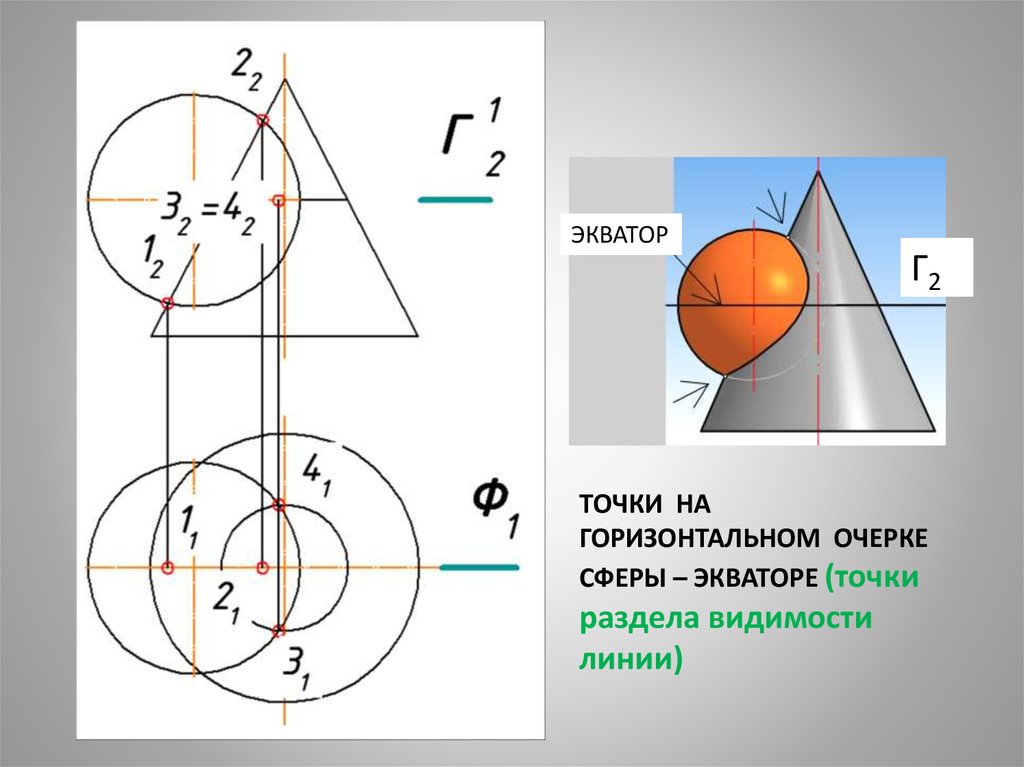
ЭКВАТОРГ2
ТОЧКИ НА
ГОРИЗОНТАЛЬНОМ ОЧЕРКЕ
СФЕРЫ – ЭКВАТОРЕ (точки
раздела видимости
линии)
13.
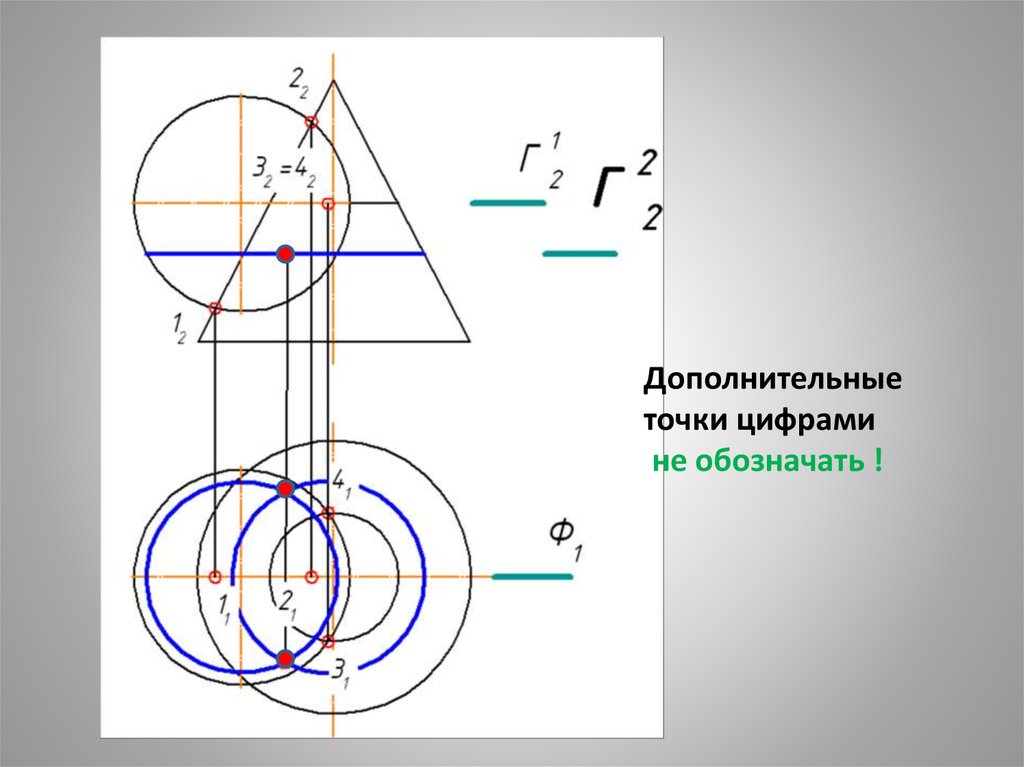
Дополнительныеточки цифрами
не обозначать !
14.
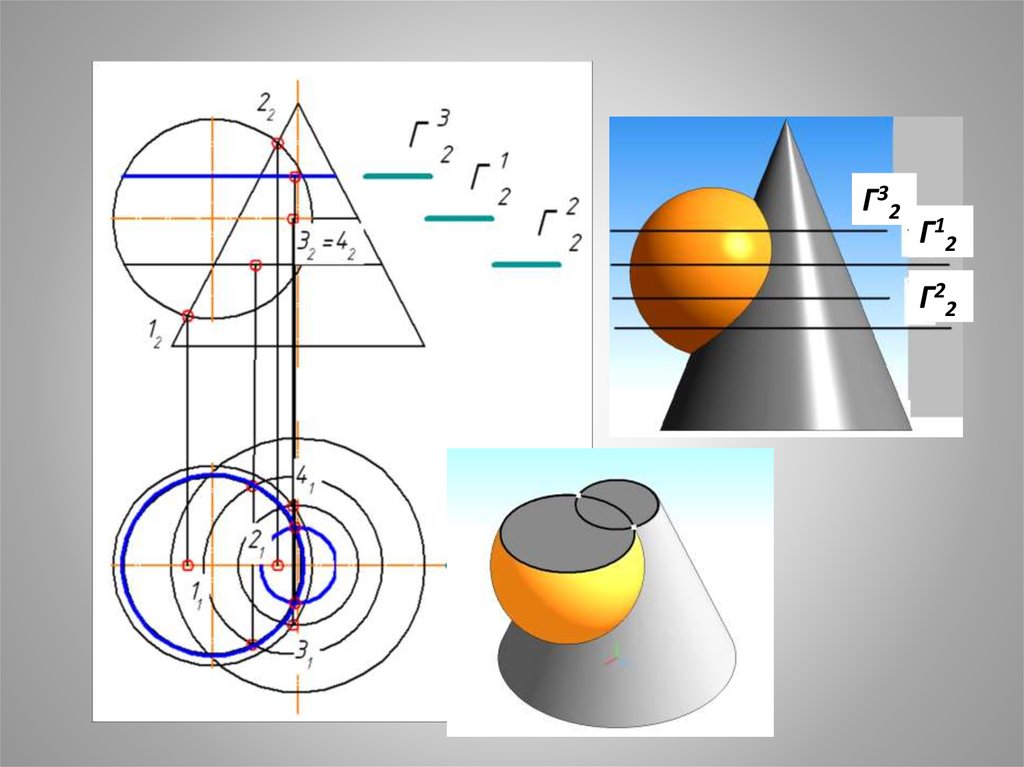
Г32Г12
Г22
15.
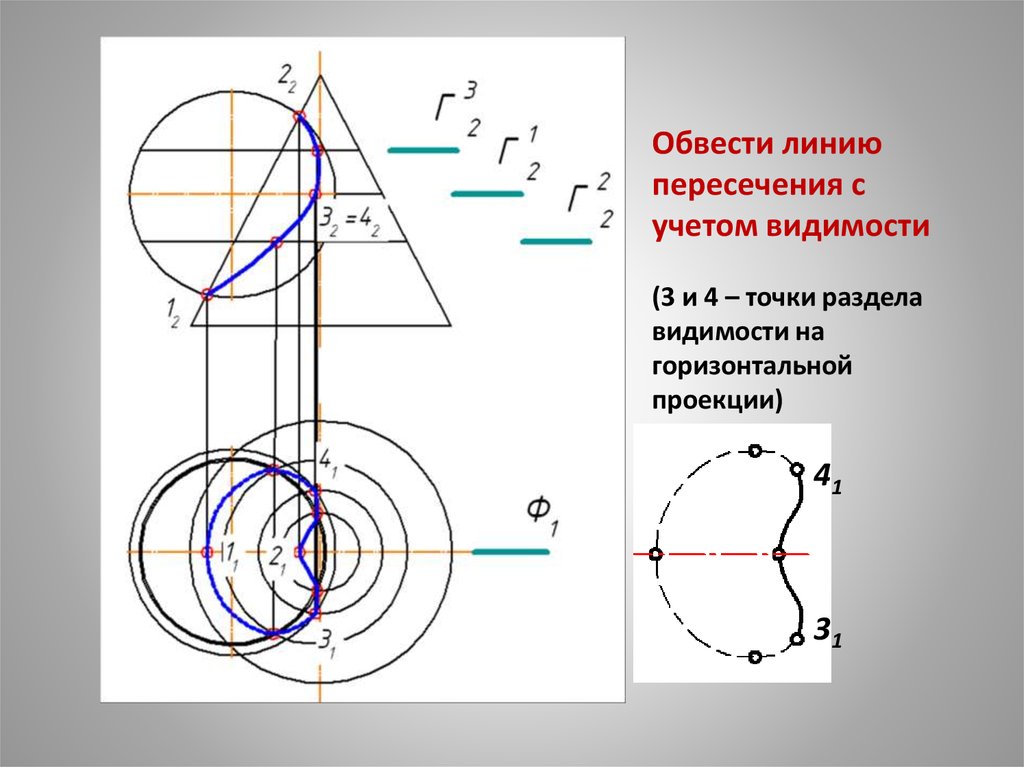
Обвести линиюпересечения с
учетом видимости
(3 и 4 – точки раздела
видимости на
горизонтальной
проекции)
41
31
16.
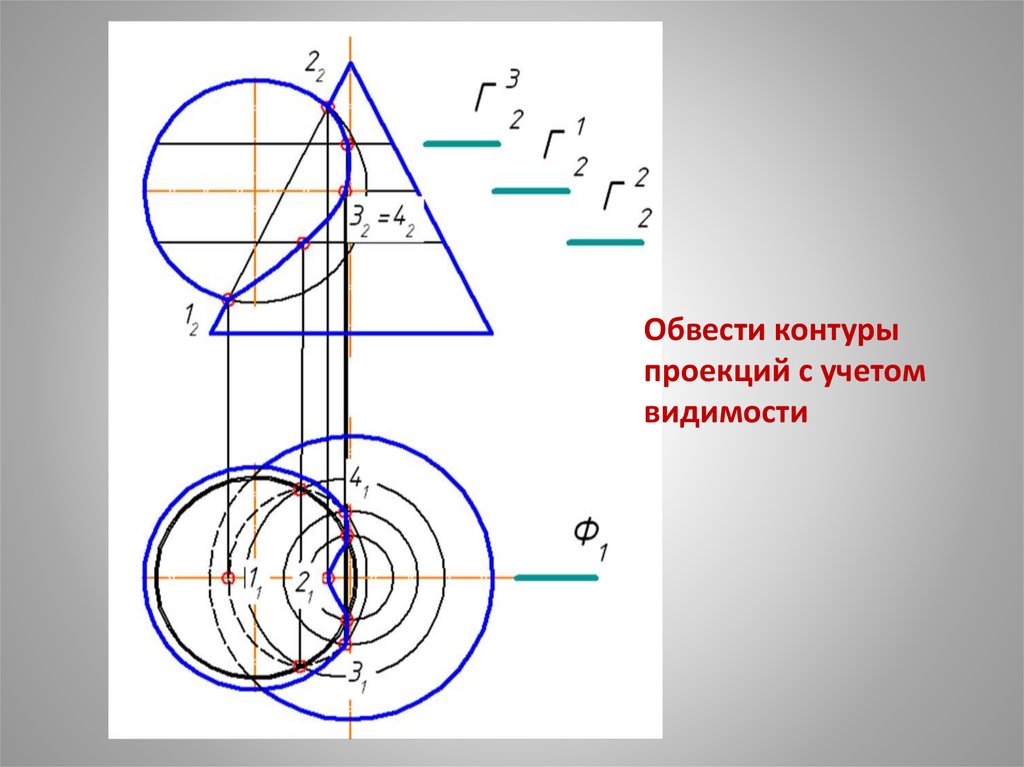
Обвести контурыпроекций с учетом
видимости
17. Пересечение поверхностей, описанных вокруг одной сферы
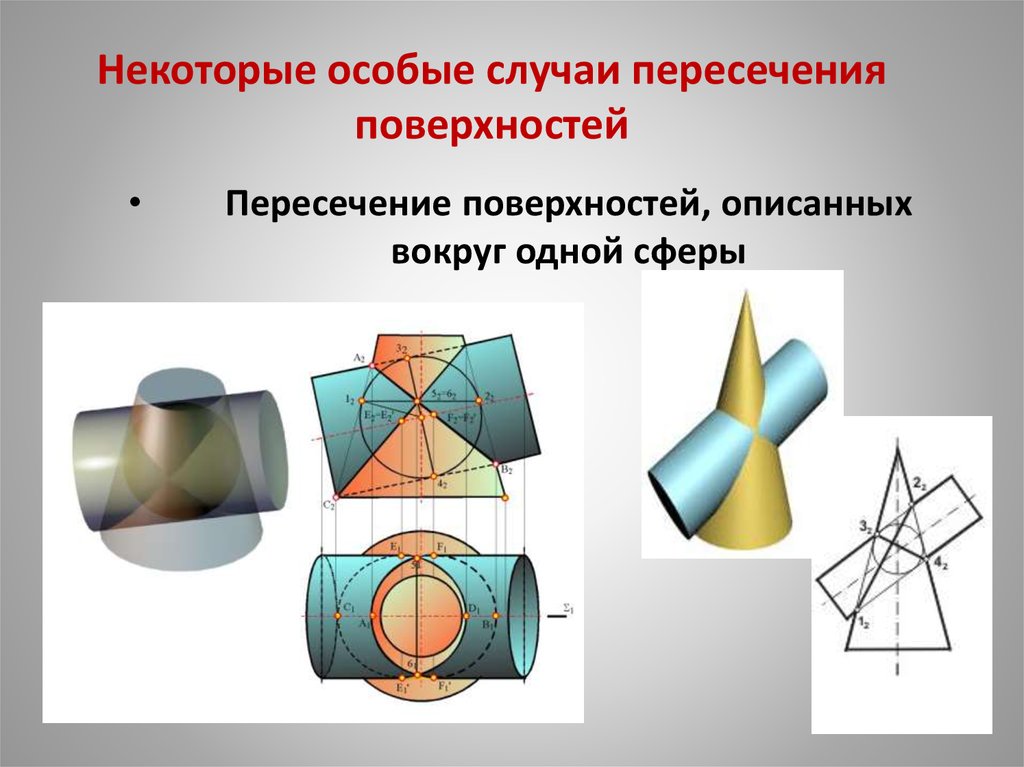
Некоторые особые случаи пересеченияповерхностей
Пересечение поверхностей, описанных
вокруг одной сферы
18. Теорема Монжа. Если две поверхности второго порядка описаны около третьей или вписаны в нее, то линия пересечения распадается на две плоск
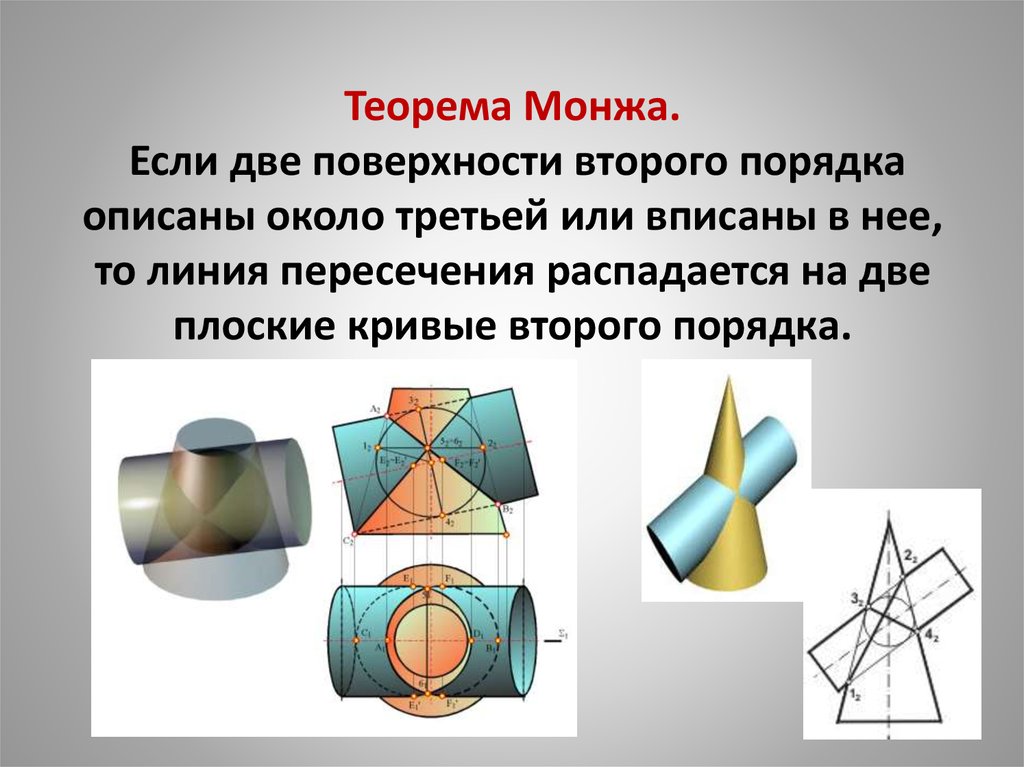
Теорема Монжа.Если две поверхности второго порядка
описаны около третьей или вписаны в нее,
то линия пересечения распадается на две
плоские кривые второго порядка.
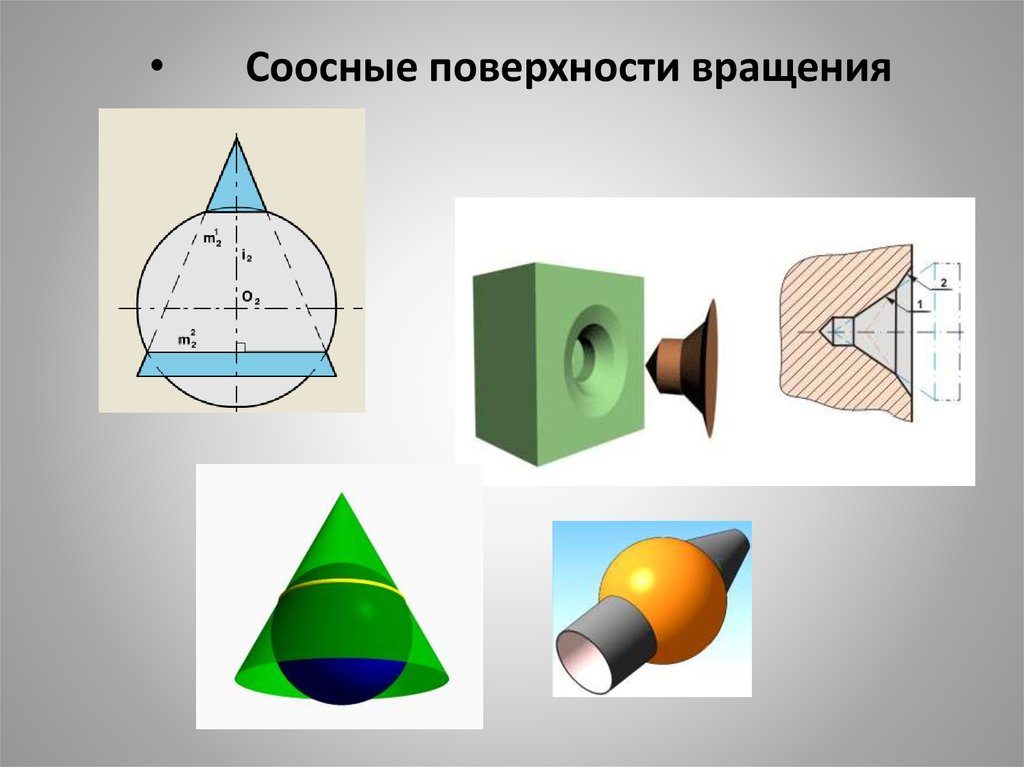
19. Соосные поверхности вращения
Соосные поверхности вращения
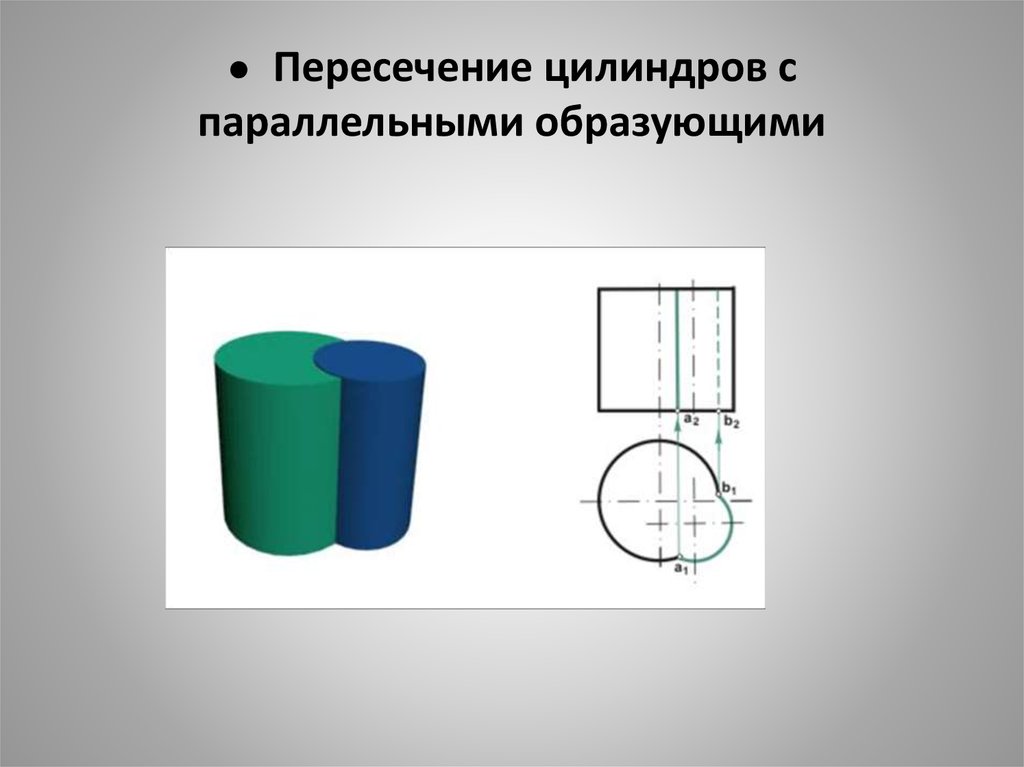
20. ● Пересечение цилиндров с параллельными образующими
21. Построение линии пересечения поверхностей способом сфер
22. КОМПЛЕКС УСЛОВИЙ для ПРИМЕНЕНИЯ СПОСОБА СФЕР : 1. Пересечение только поверхностей вращения 2. Наличие общей точки для осей поверхностей , о
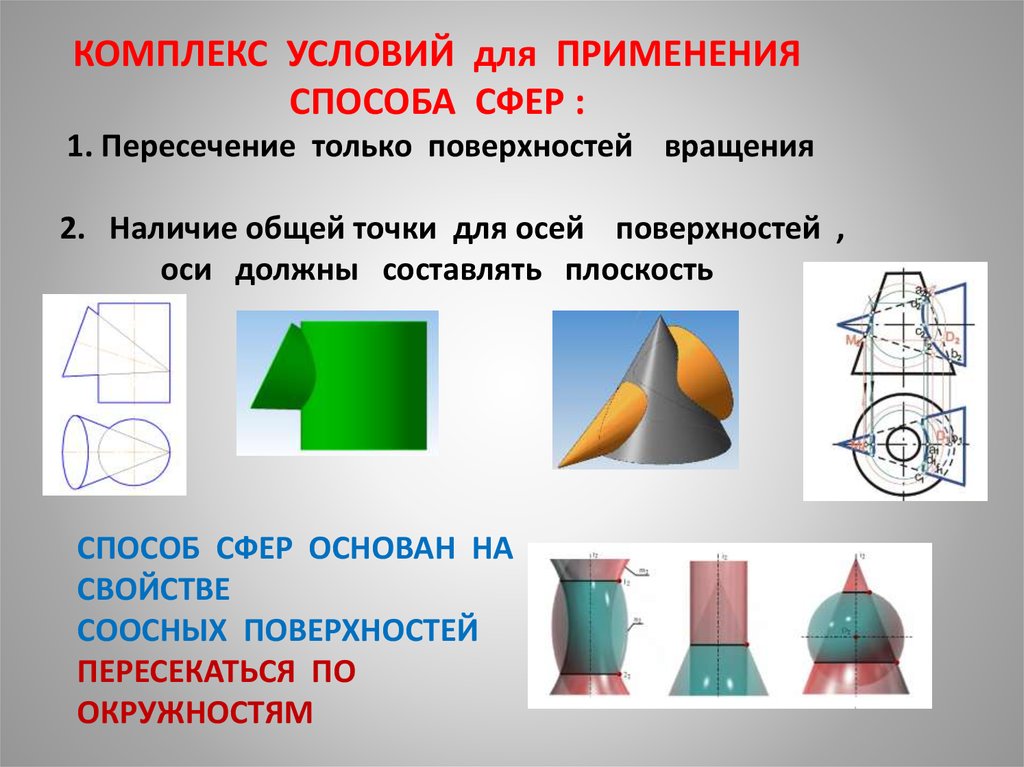
КОМПЛЕКС УСЛОВИЙ для ПРИМЕНЕНИЯСПОСОБА СФЕР :
1. Пересечение только поверхностей вращения
2. Наличие общей точки для осей поверхностей ,
оси должны составлять плоскость
СПОСОБ СФЕР ОСНОВАН НА
СВОЙСТВЕ
СООСНЫХ ПОВЕРХНОСТЕЙ
ПЕРЕСЕКАТЬСЯ ПО
ОКРУЖНОСТЯМ
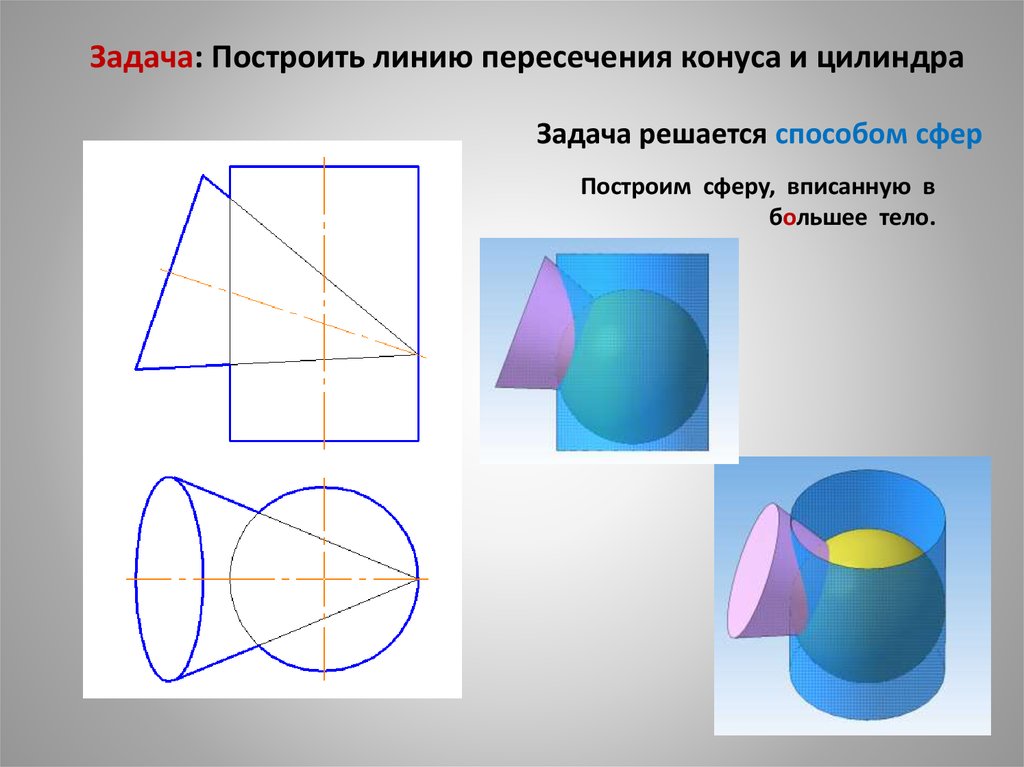
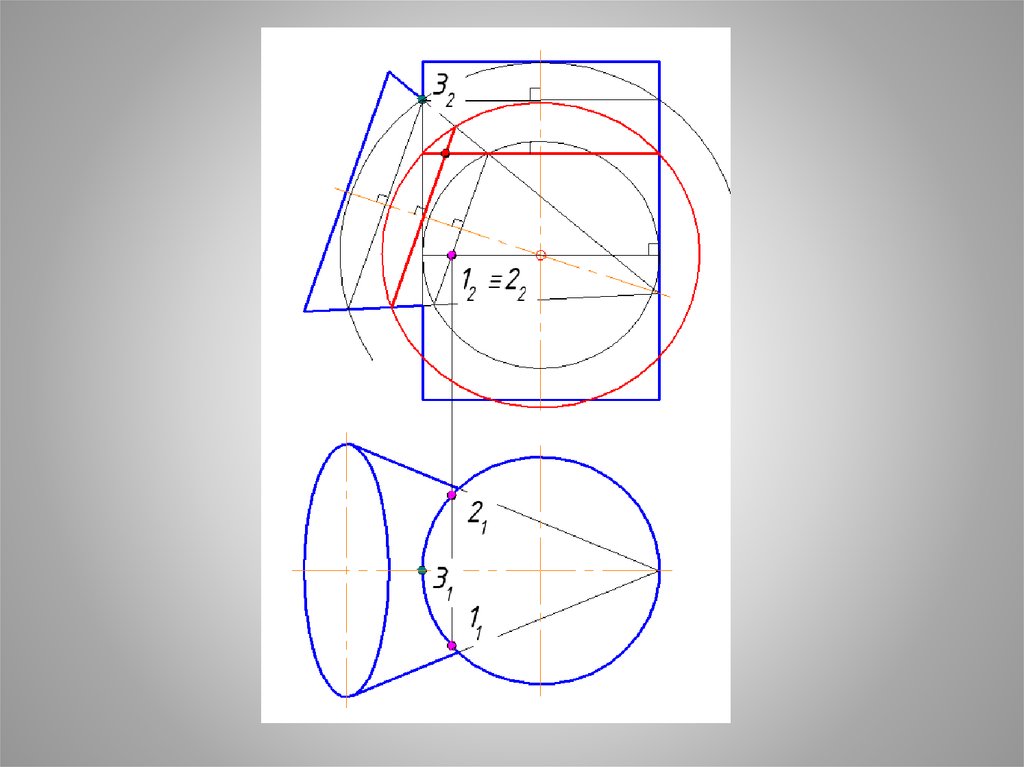
23. Задача: Построить линию пересечения конуса и цилиндра Задача решается способом сфер
Построим сферу, вписанную вбольшее тело.
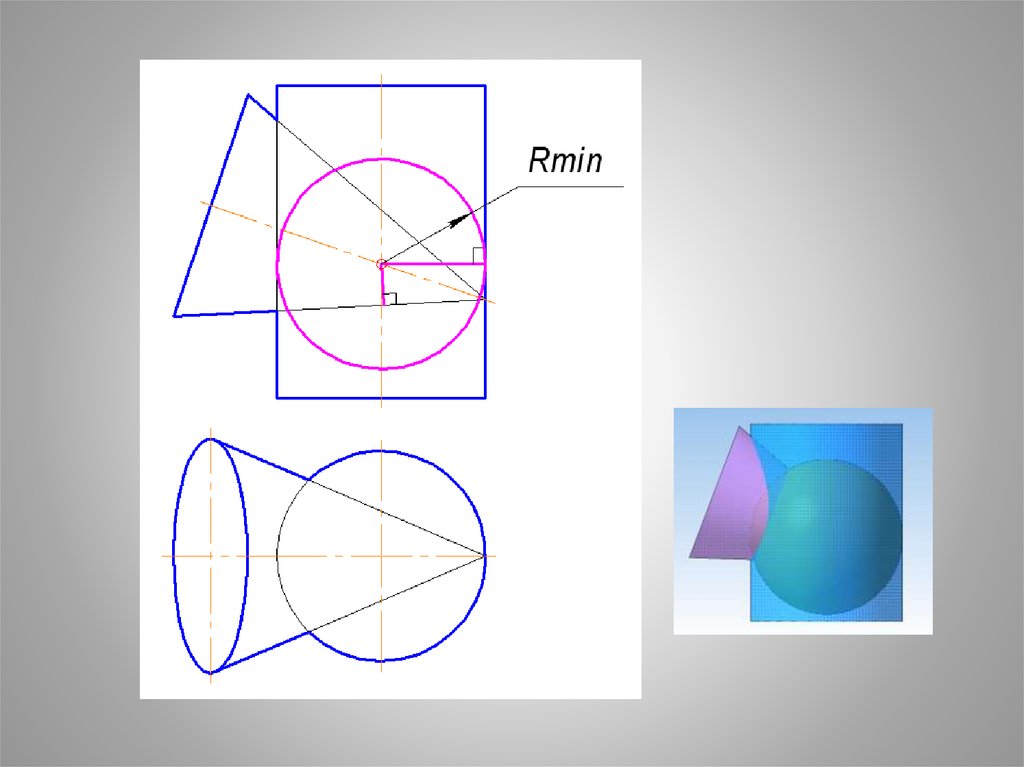
24. Центр сферы - точка пересечения осей поверхностей. Радиус вписанной сферы определить ч/з перпендикуляр, опущенный из точки пересечения осе
Центр сферы - точкапересечения осей
поверхностей.
Радиус вписанной
сферы определить ч/з
перпендикуляр,
опущенный из точки
пересечения осей на
образующую большей
поверхности.
25.
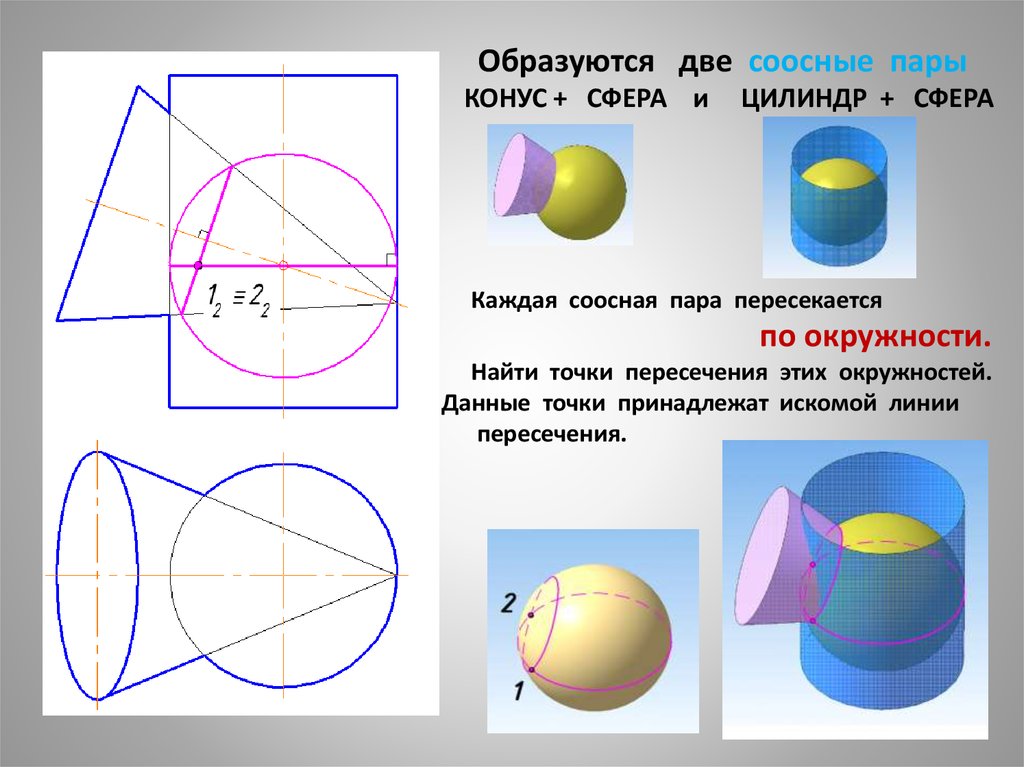
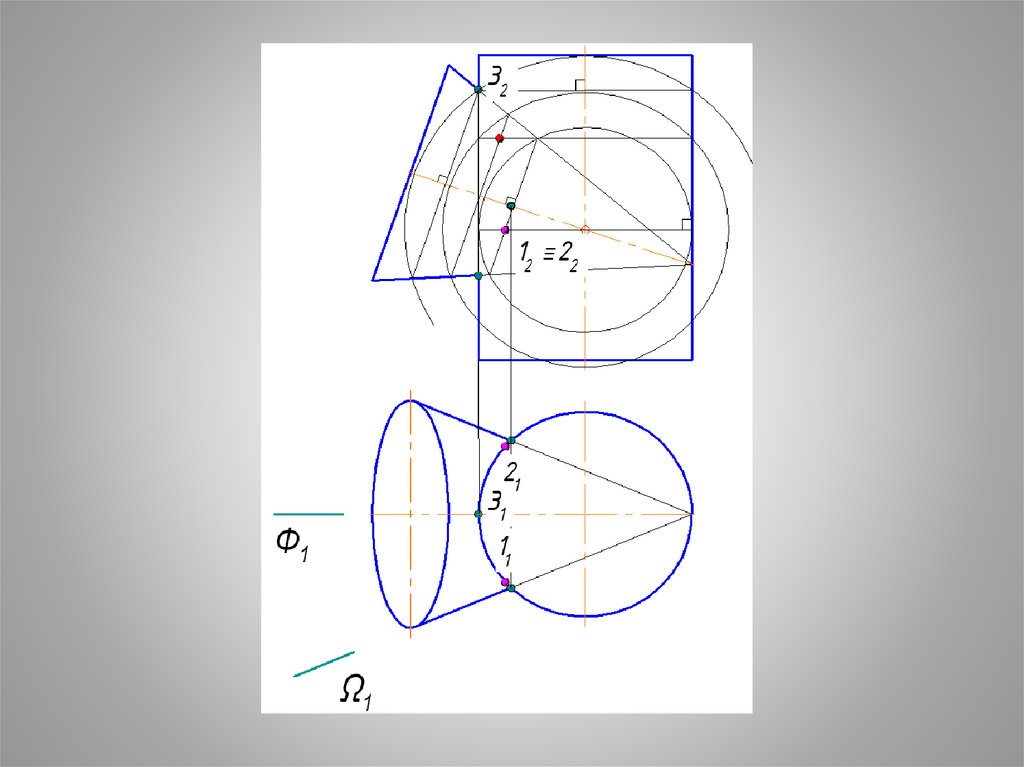
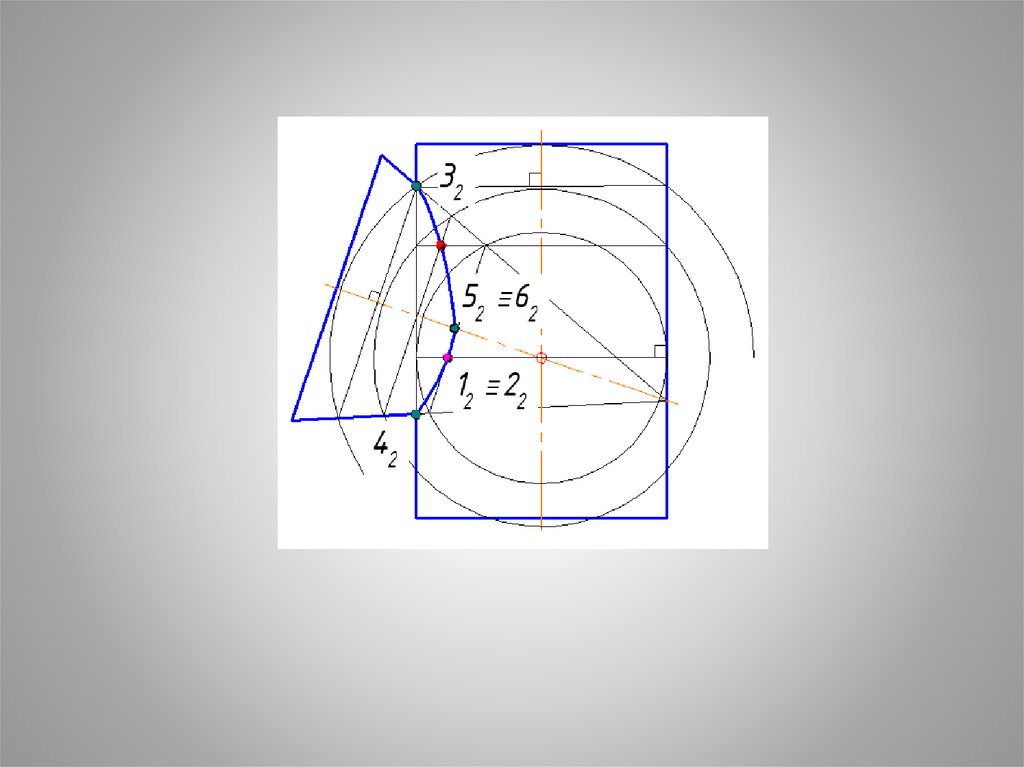
26. Образуются две соосные пары КОНУС + СФЕРА и ЦИЛИНДР + СФЕРА
Каждая соосная пара пересекаетсяпо окружности.
Найти точки пересечения этих окружностей.
Данные точки принадлежат искомой линии
пересечения.







 Математика
Математика








